6.4: The Crystaline Struture of Ionic Compounds

Last updated
Save as PDF

Page ID: 366504

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Learning Objectives

Describe ionic compounds as an extended three dimensional array (a lattice structure).
Explain that the formula of an ionic compound specifies the ratio of cations to anions.
Given the name of an ionic compound (which may contain a fixed-charge or variable charge metal and may contain a polyatomic ion) write the formula.

Recognizing Ionic Compounds

There are two ways to recognize ionic compounds. First, compounds between metal and nonmetal elements are usually ionic. For example, CaBr₂ contains a metallic element (calcium, a group 2 metal) and a nonmetallic element (bromine, a group 17 nonmetal). Therefore, it is most likely an ionic compound. (In fact, it is ionic.) In contrast, the compound NO₂ contains two elements that are both nonmetals (nitrogen, from group 15, and oxygen, from group 16). It is not an ionic compound; it belongs to the category of covalent compounds discussed elsewhere. Also note that this combination of nitrogen and oxygen has no electric charge specified, so it is not the nitrite ion.

Second, if you recognize the formula of a polyatomic ion in a compound, the compound is ionic. For example, if you see the formula \(\ce{Ba(NO3)2}\), you may recognize the “NO₃” part as the nitrate ion, \(\rm{NO_3^−}\). (Remember that the convention for writing formulas for ionic compounds is not to include the ionic charge.) This is a clue that the other part of the formula, \(\ce{Ba}\), is actually the \(\ce{Ba^{2+}}\) ion, with the +2 charge balancing the overall −2 charge from the two nitrate ions. Thus, this compound is also ionic.

Example \(\PageIndex{3}\)

Identify each compound as ionic or not ionic.

\(\ce{Na2O}\)
\(\ce{PCl3}\)
\(\ce{NH4Cl}\)
\(\ce{OF2}\)

Solution

Sodium is a metal, and oxygen is a nonmetal; therefore, \(\ce{Na2O}\) is expected to be ionic.
Both phosphorus and chlorine are nonmetals. Therefore, \(\ce{PCl3}\) is not ionic.
The \(\ce{NH4}\) in the formula represents the ammonium ion, \(\ce{NH4^{+}}\), which indicates that this compound is ionic.
Both oxygen and fluorine are nonmetals. Therefore, \(\ce{OF2}\) is not ionic.

Exercise \(\PageIndex{3}\)

Identify each compound as ionic or not ionic.

\(\ce{N2O}\)
\(\ce{FeCl3}\)
\(\ce{(NH4)3PO4}\)
\(\ce{SOCl2}\)

Answer a:: not ionic
Answer b:: ionic
Answer c:: ionic
Answer d:: not ionic

The Crystaline Structure of Ionic Compounds

Ionic compounds exist as alternating positive and negative ions in regular, three-dimensional arrays called crystals (Figure \(\PageIndex{1}\)). As you can see, there are no individual \(\ce{NaCl}\) “particles” in the array; instead, there is a continuous lattice of alternating sodium and chloride ions. However, we can use the ratio of sodium ions to chloride ions, expressed in the lowest possible whole numbers, as a way of describing the compound. In the case of sodium chloride, the ratio of sodium ions to chloride ions, expressed in lowest whole numbers, is 1:1, so we use \(\ce{NaCl}\) (one \(\ce{Na}\) symbol and one \(\ce{Cl}\) symbol) to represent the compound. Thus, \(\ce{NaCl}\) is the chemical formula for sodium chloride, which is a concise way of describing the relative number of different ions in the compound. A macroscopic sample is composed of myriads of NaCl pairs; each individual pair called a formula unit. Although it is convenient to think that \(\ce{NaCl}\) crystals are composed of individual \(\ce{NaCl}\) units, Figure \(\PageIndex{1}\) shows that no single ion is exclusively associated with any other single ion. Each ion is surrounded by ions of opposite charge.

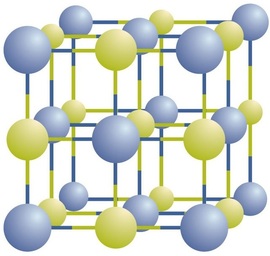
Figure 1.jpg — Figure \(\PageIndex{1}\): A Sodium Chloride Crystal. A crystal contains a three-dimensional array of alternating positive and negative ions. The precise pattern depends on the compound. A crystal of sodium chloride, shown here, is a collection of alternating sodium and chlorine ions.

The formula for an ionic compound follows several conventions. First, the cation is written before the anion. Because most metals form cations and most nonmetals form anions, formulas typically list the metal first and then the nonmetal. Second, charges are not written in a formula. Remember that in an ionic compound, the component species are ions, not neutral atoms, even though the formula does not contain charges. Finally, the proper formula for an ionic compound always has a net zero charge, meaning the total positive charge must equal the total negative charge. To determine the proper formula of any combination of ions, determine how many of each ion is needed to balance the total positive and negative charges in the compound.

This rule is ultimately based on the fact that matter is, overall, electrically neutral.

By convention, assume that there is only one atom if a subscript is not present. We do not use 1 as a subscript.

If we look at the ionic compound consisting of lithium ions and bromide ions, we see that the lithium ion has a 1+ charge and the bromide ion has a −1 charge. Only one ion of each is needed to balance these charges. The formula for lithium bromide is \(\ce{LiBr}\).

When an ionic compound is formed from magnesium and oxygen, the magnesium ion has a 2+ charge, and the oxygen atom has a −2 charge. Although both of these ions have higher charges than the ions in lithium bromide, they still balance each other in a one-to-one ratio. Therefore, the proper formula for this ionic compound is \(\ce{MgO}\).

Now consider the ionic compound formed by magnesium and chlorine. A magnesium ion has a +2 charge, while a chlorine ion has a −1 charge:

\[\ce{Mg^{2+}Cl^{−}}\]

Combining one ion of each does not completely balance the positive and negative charges. The easiest way to balance these charges is to assume the presence of two chloride ions for each magnesium ion:

\[\ce{Mg^{2+} Cl^{−} Cl^{−}}\]

Now the positive and negative charges are balanced. We could write the chemical formula for this ionic compound as \(\ce{MgClCl}\), but the convention is to use a numerical subscript when there is more than one ion of a given type—\(\ce{MgCl2}\). This chemical formula says that there are one magnesium ion and two chloride ions in this formula. (Do not read the “Cl₂” part of the formula as a molecule of the diatomic elemental chlorine. Chlorine does not exist as a diatomic element in this compound. Rather, it exists as two individual chloride ions.) By convention, the lowest whole number ratio is used in the formulas of ionic compounds. The formula \(\ce{Mg2Cl4}\) has balanced charges with the ions in a 1:2 ratio, but it is not the lowest whole number ratio.

By convention, the lowest whole-number ratio of the ions is used in ionic formulas.

For compounds in which the ratio of ions is not as obvious, the subscripts in the formula can be obtained by crossing charges: use the absolute value of the charge on one ion as the subscript for the other ion. This method is shown schematically in Figure 3.3.2.

Figure \(\PageIndex{2}\): Crossing charges. One method for obtaining subscripts in the empirical formula is by crossing charges.

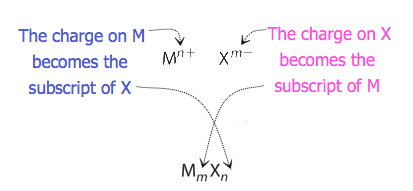
When crossing charges, it is sometimes necessary to reduce the subscripts to their simplest ratio to write the empirical formula. Consider, for example, the compound formed by Pb⁴⁺ and O²⁻. Using the absolute values of the charges on the ions as subscripts gives the formula Pb₂O₄. This simplifies to its correct empirical formula PbO₂. The empirical formula has one Pb⁴⁺ ion and two O²⁻ ions.

Example \(\PageIndex{1}\)

Write the chemical formula for an ionic compound composed of each pair of ions.

the sodium ion and the sulfur ion
the aluminum ion and the fluoride ion
the 3+ iron ion and the oxygen ion

Solution

Sodium forms an ion with a +1 charge, while the sulfur ion has a −2 charge. Two sodium +1 ions are needed to balance the −2 charge on the sulfur ion. Rather than writing the formula as \(\ce{NaNaS}\), we shorten it by convention to \(\ce{Na2S}\).
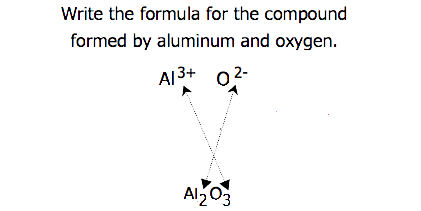
The aluminum ion has a +3 charge, while the fluoride ion formed by fluorine has a −1 charge. Three fluorine −1 ions are needed to balance the +3 charge on the aluminum ion. This combination is written as \(\ce{AlF3}\).
Iron can form two possible ions, but the ion with a +3 charge is specified here. The oxygen atom has a −2 charge as an ion. To balance the positive and negative charges, we look to the least common multiple—6: two iron +3 ions will give +6, while three −2 oxygen ions will give −6, thereby balancing the overall positive and negative charges. Thus, the formula for this ionic compound is \(\ce{Fe2O3}\). Alternatively, use the crossing charges method shown in Figure 3.3.2.

Exercise \(\PageIndex{1}\)

Write the chemical formula for an ionic compound composed of each pair of ions.

the calcium ion and the oxygen ion
the +2 copper ion and the sulfur ion
the +1 copper ion and the sulfur ion

Answer a:: CaO
Answer b:: CuS
Answer c:: Cu₂S

Formula that Contain Polyatomic Ions

The rule for constructing formulas for ionic compounds containing polyatomic ions is the same as for formulas containing monatomic (single-atom) ions: the positive and negative charges must balance. If more than one of a particular polyatomic ion is needed to balance the charge, the entire formula for the polyatomic ion must be enclosed in parentheses, and the numerical subscript is placed outside the parentheses. This is to show that the subscript applies to the entire polyatomic ion. Two examples are shown below:

Example \(\PageIndex{2}\)

Write the chemical formula for an ionic compound composed of each pair of ions.

a potassium ion and a sulfate ion
a calcium ion and a nitrate ion
a magnesium ion and a hydroxide ion

Solution

Potassium ions have a charge of +1, while sulfate ions have a charge of −2. We will need two potassium ions to balance the charge on the sulfate ion, so the proper chemical formula is \(\ce{K_2SO_4}\).
Calcium ions have a charge of +2, while nitrate ions have a charge of −1. We will need two nitrate ions to balance the charge on each calcium ion. The formula for nitrate must be enclosed in parentheses. Thus, we write \(\ce{Ca(NO3)2}\) as the formula for this ionic compound.
Magnesium ions have a +2 charge and hydroxide ions have a -1 charge. Two hydroxide ions are therefore needed to balance one magnesium ion. The formula for hydroxide must be in parenthesis because two of them appear in the formula. The chemical formula is \(\ce{Mg(OH)2}\)

Exercise \(\PageIndex{2}\)

Write the chemical formula for an ionic compound composed of each pair of ions.

a magnesium ion and a carbonate ion
an aluminum ion and an acetate ion
a zinc ion and a cyanide ion

Answer a:: Mg²⁺ and CO₃²^- = MgCO₃
Answer b:: Al³⁺ and C₂H₃O₂^-= Al(C₂H₃O₂)₃
Answer c:: Zn²⁺ and CN^-= Zn(CN)₂