2.2.1: Characteristics of gases
- Last updated
- Save as PDF
- Page ID
- 419254
What is a gas
Gas is one of the four states of matter that falls between the liquid and the plasma state. The air around us is a gas composed of ~78% nitrogen (N2), ~21% oxygen, and the remaining ~1% are other gases, including carbon dioxide, water vapors, argon, etc., as illustrated in Fig. 7.1.1.
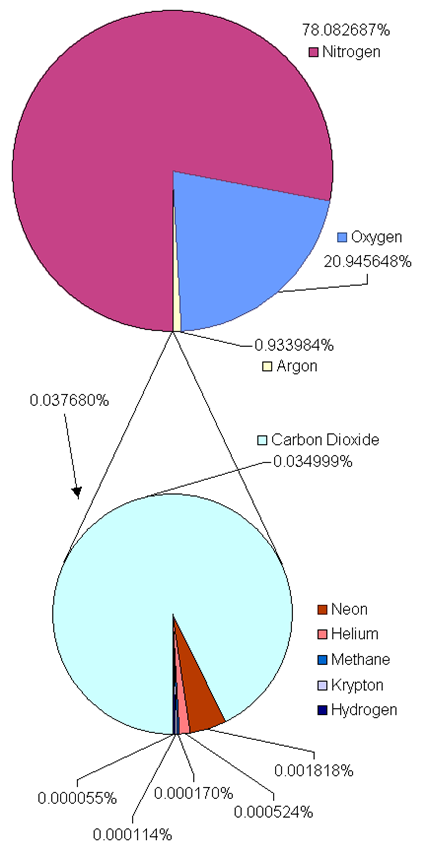
Elements that exist as gases at room temperature and atmospheric pressure include noble gases which are monoatomic molecules including helium (He), neon (Ne), argon (Ar), krypton (Kr), xenon (Xe), and radon (Rn), and diatomic elemental molecules that include hydrogen (H2), nitrogen (N2), oxygen (O2), and two halogens: fluorine (F2) and chlorine (Cl2). Several molecular compounds exist as gases at room temperature, e.g., carbon dioxide (CO2), carbon monoxide (CO), methane (CH4), nitrogen dioxide (NO2), sulfur dioxide (SO2), hydrogen sulfide (H2S), ammonia (NH3).
The properties of gases are defined by their amount in moles (n), volume (V), temperature (T), and pressure (P). These parameters are described in the following.
The amount of a gas
The amount of gas is measured in moles (n), i.e., 6.022 x 1023 molecules of a gas is one mole of the gas. The gas has mass and can be measured in mass units like grams or kilograms, but the mass needs to be divided by the molar mass of the gas to obtain the amount in moles for calculations.
Note
The amount of gas in moles is needed in gas laws because the properties of gases are proportional to the number of molecules, not to the masses of the molecules.
Example \(\PageIndex{1}\)
How many moles are in 10.0 g of oxygen gas?
Solution
Step 1. Given: Mass = 10.0 g O2, Desired: ? moles of O2.
Step 2. Equality between the given and the desired units: 1 mole of O2 = 32.00 g O2.
Step 3. The conversion factors from the equality: \(\frac{1~mol~O_2}{32.00~g~O_2}\) and \(\frac{32.00~g~O_2}{1~mol~O_2}\)
Step 4. Multiply the given quantity with the conversion factor that cancels the given and leaves the desired unit in the answer: \[10.0 \cancel{~g~O_2)}\times\frac{1~mol~O_2}{32.00\cancel{~g~O_2}} = 0.312 ~g~O_2\nonumber\]
The volume of a gas
Volume (V) is the space a substance occupies. The SI unit of volume is a meter cube (m3), i.e., the space inside of a 1m x 1m x 1m cube.
Usually, the volume is reported in liters (L), which is dm3, or milliliter (mL), which is cm3. The relationship between the volume units is the following.
\[1 \mathrm{~m}^{3}=1000 \mathrm{~L}\nonumber\]
\[1 \mathrm{~L}=1000 \mathrm{~mL}\nonumber\]
The gases do not have a fixed shape or volume. The gases acquire the shape of the container. The gases expand or contract to fill the available space in a container.
The temperature of a gas
The temperature (T) is a measure of how hot or cold an object is.
The temperature is a manifestation of the thermal energy of a substance. Thermal energy is a source of heat. Heat is the flow of energy from a hot to a cold object. The SI unit of temperature is Kelvin (K) which has a value of 273.15 K at the freezing point of water and 375.15 K at the boiling point of water. The zero of the kelvin scale is called the absolute zero at which no more energy can flow out of a substance as heat. There is no negative number on the kelvin scale of temperature.
Other commonly used units of temperature are Celsius (oC) which has a value of 0 oC at the freezing point of water and 100 oC at the boiling point of water. The relationship between temperature in kelvin (TK) and the temperature in Celsius (TC) is the following.
\[T_{K}=T_{C}+273.15\nonumber\]
Fahrenheit is a temperature scale used in the English system of measurement that has a value of 32 oF at the freezing point of water and 212 oF at the boiling point of water. The relationship between the temperature in Fahrenheit (TF) and the temperature in Celsius (TC) is the following.
\[T_{F}=\frac{9}{5} T_{C}+32\nonumber\]
Note
The temperature in Kelvin (K) is used in the gas law calculations.
The pressure of a gas
Pressure (P) is the force (F) per unit area (A), i.e., \(P = \frac{F}{A}\).
The matter has mass and applies a force, which is the weight due to gravitational pull. For example, a column 1 m x 1m at sea level and height equal to the earth’s atmosphere, as illustrated in Fig. 7.1.2 has a mass of ~10,000 kg. Mercury (Hg) filled in a column of 1 m x 1m and height 0.760 m has the same mass as the mass of air of 1 m x 1 m column extending from the sea level to the entire atmosphere of the earth.

A column of air extending from sea level to the entire atmosphere applied pressure equal to one atmosphere (atm), where atm is the pressure unit. One atmosphere (atm) is equal to 760 millimeter of mercury (mmHg), where mmHg is another unit of pressure. One mmHg is also called Torr. The relationship between atm, mmHg, and Torr is the following.
\[1\mathrm{~atm}=760 \mathrm{~mmHg} = 760 \mathrm{~Torr}\nonumber\]
Pascal (Pa)
The SI unit of pressure is pascal (Pa), which is pressure (P) applied by a force (F) of one newton (N) on an area of one meter square (m2). Mathematical form of the unit is: \(1 ~Pascal = \frac{1~Newton}{1 ~meter-square}\) or \(Pa = \frac{N}{m^2}\)
Kilopascal is 1000 Pa, and kilopascal is also called the bar. The English system unit of pressure is pound-force per square inch (psi). The relationship between different units of pressure mentioned above is the following.
\[1 \mathrm{~atm}=760 \mathrm{~mm} \mathrm{Hg}=760 \mathrm{~Torr}=1.01325 \times 10^{5} \mathrm{~Pa}=1.01325 \times 10^{2} \mathrm{~kP}=1.01325 \mathrm{~bar}=14.7 \mathrm{~psi}\nonumber\]
These relationships are changed to conversion factors that allow conversion from one to another pressure unit, as explained in the following examples.
Example \(\PageIndex{2}\)
Express 51 mm Hg in a) atm and b) in Pa.
Solution
Given: Pressure = 51 mm Hg. Required: pressure in atm and Pa
Relationship between mm Hg and atm: \(1\mathrm{~atm}=760 \mathrm{~mm Hg}\nonumber\)
The conversion factors from the equality: \(\frac{1 \mathrm{~atm}}{760 \mathrm{~mm} \mathrm{Hg}}\nonumber\) and \(\frac{760 \mathrm{~mm} \mathrm{Hg}}{1 \mathrm{~atm}}\nonumber\)
Calculations: multiply the given quantity with the conversion factor that cancels the given unit and leaves the desired unit in the answer.
\[51 \cancel{\mathrm{~mm} \mathrm{Hg}} \times \frac{1 \mathrm{~atm}}{760 \cancel{\mathrm{~mm} \mathrm{Hg}}}=6.7 \times 10^{-2} \mathrm{~atm}\nonumber\]
Similarly, the relationship between mm Hg and Pa: \(760 \mathrm{~mm Hg}=1.01325 \times 10^{5} \mathrm{~Pa}\nonumber\)
The conversion factors from the equality: \(\frac{760 \mathrm{~mm Hg}}{1.01325 \times 10^{5} \mathrm{~Pa}}\nonumber\) and \(\frac{1.01325 \times 10^{5} \mathrm{~Pa}}{760 \mathrm{~mm Hg}}\nonumber\)
Calculations: multiply the given quantity with the conversion factor that cancels the given unit and leaves the desired unit in the answer.
\[51 \cancel{\mathrm{~mm} \mathrm{Hg}} \times \frac{1.01325 \times 10^{5} \mathrm{~Pa}}{760 \cancel{\mathrm{~mm} \mathrm{Hg}}}=6.8 \times 10^{3} \mathrm{~Pa}\nonumber\]
Measurement of gas pressure
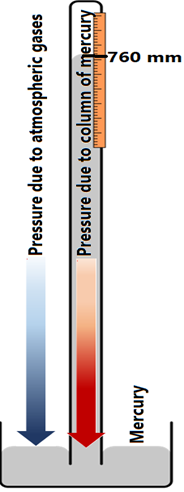
The instrument used to measure the atmospheric pressure is called a barometer.
The barometer, shown in Fig. 7.1.3, was invented by Evangelista Torricelli. It is a glass tube that is more than 760 mm long and closed at one end. The glass tube is filled with mercury and inverted to dip its open end in a dish that contains a layer of mercury. The mercury falls from the tube due to its weight but stops falling when the column of mercury is 760 mm in height at sea level due to the atmospheric pressure pushing it back into the tube. Remember 760 mmHg = 1 atm. Above 760 mm is a vacuum in the tube.
The pressure of gases in a laboratory is usually measured using an instrument called a manometer.
A manometer is a U-shaped glass tube partially filled with mercury, as shown in Fig. 7.1.4. One end of the U-tube is connected to a gas chamber in which pressure is being measured, and the other end is either closed (with a vacuum on the closed end), called a closed-ended manometer, or it is open to the atmosphere, called an open-ended manometer.
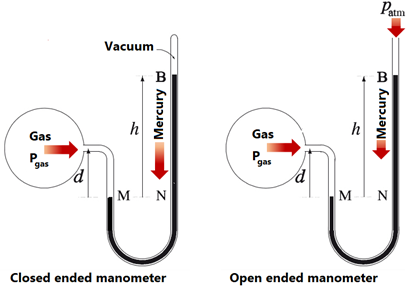
In the case of a closed-ended manometer, the gas pressure is equal to the difference in the height of mercury in the two arms of the U-tube in mmHg, i.e., height (h) from point N to point B in mm units as shown in Fig. 7.1.4.
Example \(\PageIndex{3}\)
Calculate the pressure in atm for the gas shown in Fig. 7.1.4 in the closed-ended manometer if h = 40 mm?
Solution
In a closed-ended manometer, the gas pressure is equal to the height h in mm Hg: P = 40 mm Hg.
Pressure in atm:
\[40 \cancel{\mathrm{~mm} \mathrm{Hg}} \times \frac{1 \mathrm{~atm}}{760 \cancel{\mathrm{~mm} \mathrm{Hg}}}=5.3 \times 10^{-2} \mathrm{~atm}\nonumber\]
In the case of an open-ended manometer, the gas pressure is equal to the difference in the height of mercury in the two arms of the U-tube in mm of Hg plus the atmospheric pressure outside expressed in mm of Hg.
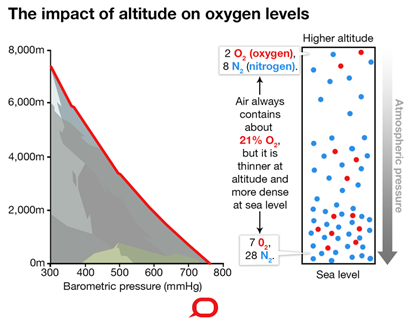
Variation of air pressure with altitude
The air pressure decreases, and the gas concentration decreases as the altitude increases, as illustrated in Fig. 7.1.5. The oxygen concentration in the air also decreases as the altitude increases. That is why mountain climbers experience an inadequate supply of oxygen to the body at high altitudes -a medical condition called hypoxia.
Blood pressure
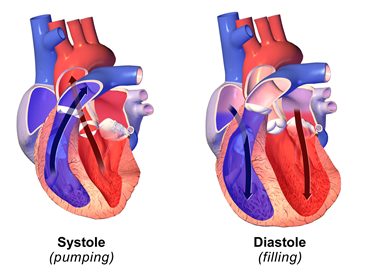
The heart pumps the blood into the circulatory system. When the heart contracts, it applies the pressure on the blood in it, and the blood pumps out of the heart into the circulatory system, as illustrated in Fig. 7.1.6. The blood pressure in the circulatory system is highest at this point, and it is called systolic pressure. It can be in the range of 100 to 200 mm Hg. A desirable systolic pressure range is 100 to 120 mm Hg. When heart muscles relax, the cavity in the heart expands and more blood fills in the heart. The blood pressure in the circulatory system is minimum at this point, and it is called diastolic pressure. The diastolic pressure may vary in the range of 60 to 110 mm Hg. A desirable diastolic pressure is less than 80 mm Hg.
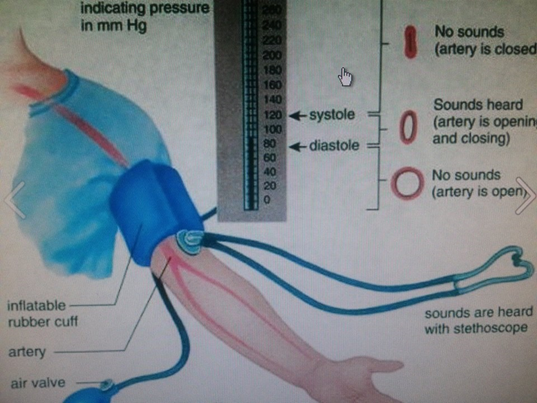
The device used to measure blood pressure is called a sphygmometer. It consists of a cuff that wraps around the upper arm, a pump to inflate air in the cuff, and a stethoscope to hear the sound of blood flow, as illustrated in Fig. 7.1.7. The cuff is inflated with air to a pressure above the systolic pressure and it results in cutting off the blood flow through the brachial artery in the upper arm. A stethoscope is used to hear the sound of blood flow. No sound is heard at this point. The pressure in the cuff is slowly reduced. When the pressure in the cuff is equal to systolic pressure, the blood begins to spurt into the artery, and a tapping sound is heard through the stethoscope. At the point when the pressure is equal to the diastolic pressure, the blood flows freely through the artery, and the tapping sound disappears. The blood pressure reading is reported as a set of two numbers, e.g., 120/80, where the higher number is systolic, and the lower number is the diastolic pressure.
Kinetic molecular theory of gases
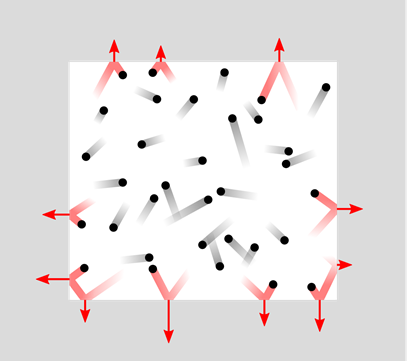
The physical characteristics of the gases are explainable by a model called the kinetic molecular theory of gases, illustrated in Fig. 7.1.8.
Postulates of kinetic molecular theory of gases
- Gases consist of particles called molecules that are far apart from each other. As a consequence of the vast distances, the intermolecular forces are negligible, and the volume occupied by the gas molecules is negligible.
- The gas molecules are moving in straight lines in random directions until they collide with another molecule or the wall of the container.
- The collisions are elastic, i.e., the total energy is conserved, but the molecules change direction and change speed after the collision. It results in the distribution of molecular speeds over a wide range.
- The average kinetic energy of the gas molecules is directly proportional to the absolute temperature. The average kinetic energy of the molecules of different gases is the same at the same temperature.
Explanation of the characteristics of the gases based on the kinetic molecular theory of gases
- Upon exposing gas to a vacuum, the gas molecules keep moving in a straight path in the vacuum until they collide with a container boundary and bounce back. It explains gases are expandable. Collisions of gas molecules with the wall exert outward pressure on the wall and, as a reaction, the wall exerts an equal inward pressure on the gas. Applying more pressure to the gas through any portion of the gas boundary disturbs the above-mentioned balance of action and reaction forces, resulting in an inward movement of the portion of the boundary surface. In other words, the gases are compressible.
- If a boundary separating two gases is removed, the random molecular motions ultimately mix the two gases making a homogeneous mixture, i.e., gases are entirely miscible with other gases.
- When temperature increases the gas molecules move faster and colloid more frequently, which explains the fact that gases exert more pressure upon heating and expand if the boundary is not rigid. The more frequent bursting of tires in summer is due to the pressure increase due to heating.
- When more gas fills in the tire, the pressure increases due to more frequent collisions. Compressing the gas into smaller volume have the same effect, i.e., the molecular collisions increase increasing the pressure.
The physical characteristics of the gases are independent of the nature of the gas molecules due to negligible intermolecular interactions but depend on four physical properties, i.e., pressure, volume, temperature, and amount of gas. The following sections describe the relationships between the physical properties of the gases.


