10.2: Hybrid Orbitals in Water
- Page ID
- 210871
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The goal of applying Valence Bond Theory to water is to describe the bonding in \(H_2O\) and account for its structure (i.e., appropriate bond angle and two lone pairs predicted from VSEPR theory).
The ground state electronic configuration of atomic oxygen atom is \(1s^2\,2s^2\,2p_x^2\,2p_y^1 \, 2p_z^1\) and of course the ground state electronic configuration of atomic hydrogen atom is \(1s^1\), i.e., a spherical atomic orbital with no preferential orientation. If only the unfilled \(2p_y\) and \(2p_z\) atomic orbitals of the oxygen were used as bonding orbitals, then two bonds would be predicted. These bonding wavefunctions would be mixture of only \(|2p_y \rangle\) and \(|2p_z \rangle\) orbitals on oxygen and the \(|1s \rangle\) orbitals on the hydrogens (\(H_1\) and \(H_2\)):
\[ | \chi_1 \rangle = a_1 |1s \rangle_{H_1} + b_1 |2p_y \rangle_O \label{wrong1}\]
\[ | \chi_2 \rangle = a_2 |1s \rangle_{H_2} + b_2 |2p_z \rangle_O \label{wrong2}\]
However, with a H-O-H bond angle for these bonds would be expected to be 90° since \(2p_y\) and \(2p_z\) are oriented 90° with respect to each other. Note that \( | \chi_1 \rangle \) and \( | \chi_2 \rangle \) are two-center bonding orbitals common to Valence Bond theory.
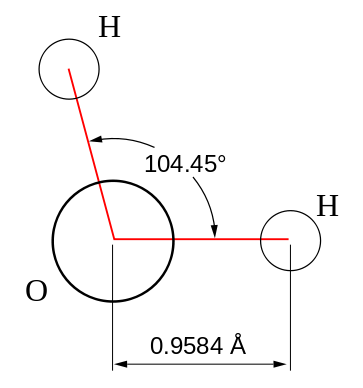
Using the oxygen atomic orbitals directly is obviously not a good model for describing bonding in water, since we know from experiment that the bond angle for water is 104.45° (Figure \(\PageIndex{2}\)), which is also in agreement with VSEPR theory. Since the \(2s\) orbital is spherical, mixing some \(2s\) character into the \(2p_z\) orbitals can adjust the bond angle as discussed previously by creating new hybrid orbitals.
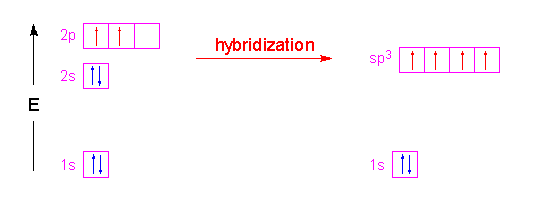
Historically, Valence Bond theory was used to explain bend angles in small molecules. Of course, it was only qualitatively correct in doing this, as the following example shows. Let us construct the Valence Bond wavefunctions for the two bonding pairs in \(H_2O\) by mixing the \(|2s \rangle\), \(|2p_x \rangle\), \(|2p_y \rangle\), and \(|2p_z \rangle\) into four new \(sp^3\) hybrid orbitals:
\[\begin{align*}\chi_1 (r) &= \dfrac{1}{2} \left[\psi_{2s}(r)+\psi_{2p_x}(r)+\psi_{2p_y}(r)+\psi_{2p_z}(r)\right]\\ \chi_2 (r) &= \dfrac{1}{2}\left[\psi_{2s}(r)-\psi_{2p_x}(r)-\psi_{2p_y}(r)+\psi_{2p_z}(r)\right]\\ \chi_3 (r) &= \dfrac{1}{2}\left[\psi_{2s}(r)+\psi_{2p_x}(r)-\psi_{2p_y}(r)-\psi_{2p_z}(r)\right]\\ \chi_4 (r) &= \dfrac{1}{2}\left[\psi_{2s}(r)-\psi_{2p_x}(r)+\psi_{2p_y}(r)-\psi_{2p_z}(r)\right]\end{align*}\]
Hence, the three \(2p\) orbitals of the oxygen atom combined with the \(2s\) orbitals of the oxygen to form four \(sp^3\) hybrid orbitals (Figure \(\PageIndex{3}\)).
The bond angle for four groups of electrons around a central atom is 109.5 degrees. However, for water the experimental bond angle is 104.45°. The VSPER picture (general chemistry) for this is that the smaller angle can be explained by the presence of the two lone-pairs of electrons on the oxygen atom. Since they take up more volume of space compared to a bonding pair of electrons the repulsions between lone pairs and bonding pairs is expected to be greater causing the H-O-H bond angle to be smaller than the ideal 109.5°.
We can rationalize this by thinking about the s and p characters of the hybrids. In a perfectly \(sp^3\) hybridized set of hybrid orbitals, each \(sp^3\) orbital should have: 25% s character and and 75% p character. Since the bond angle is not 109.5° in water, the hybrid orbitals cannot have exactly this ratio of s and p character. So there there is uneven distribution of s and p character between the 4 hybrid orbitals. First we will write down the wavefunction and see what this means and then we will rationalize it.
Hybridization is an often misconceived concept. It only is a mathematical interpretation, which explains a certain bonding situation (in an intuitive fashion). In a molecule the equilibrium geometry will result from various factors, such as steric and electronic interactions, and further more interactions with the surroundings like a solvent or external field. The geometric arrangement will not be formed because a molecule is hybridized in a certain way, it is the other way around, i.e., a result of the geometry or more precise and interpretation of the wavefunction for the given molecular arrangement.
Estimating Character of Hybrid Orbitals
The terminology we use for hybridization actually is just an abbreviation:
\[\mathrm{sp}^{x} = \mathrm{s}^{\frac{1}{x+1}}\mathrm{p}^{\frac{x}{x+1}}\]
In theory \(x\) can have any value, hence any of the following combinations constitute valid hybridization schemes for 1 s orbital and 3 p orbitals:
\[\begin{align} 1\times\mathrm{s}, 3\times\mathrm{p} \nonumber &\leadsto 4\times\mathrm{sp}^3 \nonumber\\ &\leadsto 3\times\mathrm{sp}^2, 1\times\mathrm{p} \nonumber \\ &\leadsto 2\times\mathrm{sp}, 2\times\mathrm{p} \nonumber \\ &\leadsto 2\times\mathrm{sp}^3, 1\times\mathrm{sp}, 1\times\mathrm{p} \nonumber \\ &\leadsto \text{etc. pp.} \nonumber \\ &\leadsto 2\times\mathrm{sp}^4, 1\times\mathrm{p}, 1\times\mathrm{sp}^{(2/3)} \nonumber \end{align}\]
There are virtually infinite possibilities of combinations. Which one is "valid" is only determined by experiment (e.g., structure or spectroscopy). The generic \(sp^x\) hybrid orbitals wavefunction can be roughly written in terms of atomic orbital character:
\[ |\chi_i \rangle = N ( p + \gamma s) \label{H1}\]
where \(N\) is a normalization constant and \(\gamma\) is the relative contribution of s character to the hybrid orbital. For a pure \(sp^3\) hybrid, \(\gamma\) would be 0.25 and for a pure \(sp\) hybrid, \(\gamma\) would be 1. The question is how to determine \(\gamma\) to get a better picture of the hybridization of water. Starting with the normalization criteria for wavefunctions:
\[ \langle \chi_i | \chi_i \rangle =1\]
and substituting Equation \(\ref{H1}\) into to get
\[ \langle N ( p + \gamma s) | N ( p + \gamma s) \rangle =1\]
which in integral notation is
\[ \int N^2 ( p + \gamma s)^2 d\tau =1 \]
where \(d\tau\) represents all space. This is then expanded to
\[ N^2 \cancelto{1}{\int p^2\; d\tau} + N^2 2 \gamma \cancelto{0} {\int sp\; d\tau} + N^2 \gamma^2 \cancelto{1} {\int s^2 \; d\tau} =1\label{H3} \]
These terms simplify either due to orthogonality or normality of the constitute atomic orbitals. Equation \(\ref{H3}\) simplifies to
\[ N^2 + N^2 \gamma^2 =1 \]
and thus the normalization factor can be expressed in terms of \(\gamma\)
\[ N = \dfrac{1}{\sqrt{1+\gamma^2}}\]
and the generic normalized \(sp^x\) hybrid orbital (Equation \(\ref{H1}\)) is
\[ |\chi_i \rangle = \dfrac{1}{\sqrt{1+\gamma^2}} ( p + \gamma s) \label{H4}\]
The s and p characters to a hybrid orbital are now easy to obtain by squaring \( |\chi_i \rangle \)
- The magnitude of p-character is \[ \left(\dfrac{1}{\sqrt{1+\gamma^2}} \right)^2 = \dfrac{1}{1+\gamma^2} \label{p}\] as \(\gamma \rightarrow 0\), then the p character of the hybrid goes to 100%
- The magnitude of s-character is \[ \left(\dfrac{1}{\sqrt{1+\gamma^2}} \gamma ^2 \right)^2 = \dfrac{\gamma^2}{1+\gamma^2} \label{s}\] as \(\gamma \rightarrow 1\), then the s character of the hybrid goes to 50%
As mentioned above, the geometric arrangement will not be formed because a molecule is hybridized in a certain way, it is the other way around. How do we choose the correct value of \(\gamma\) for the hybrid orbitals? The mixing coefficient \(\gamma\) is clearly related to the bond angle θ. Using some simple trigonometric relationships, it can be proven that:
\[\cos θ = - \gamma^2 \label{angle} \]
Equation \(\ref{angle}\) is an important equation as it related experimentally determined structure to the nature of the bonding and specifically, the composition of the atomic orbitals that create the hybrid orbitals used in the bonding.
What is the s-character in the hybrid orbitals for \(CO_2\).
Solution
We know from simple VSEPR theory that the geometry of \(CO_2\) is a linear triatomic molecule.
Thus \(\theta = 180°\) and via Equation \(\ref{angle}\), \(\gamma = 1\) since \(\cos 180 ° = -1\). Hence, Equation \(\ref{s}\) argues that the hybrid orbitals used in the bonding of \(CO_2\) have 50% character; i.e., they are \(sp\) hybrid orbitals
\[ | \chi_1 \rangle = \dfrac{1}{\sqrt{2}} ( s + p)\]
and
\[ | \chi_2 \rangle = \dfrac{1}{\sqrt{2}} ( s - p)\]
Now, let's apply Equation \(\ref{s}\) to water to find the character of the hybrid orbitals in water. The bond angle in water is 104.45° (Figure \(\PageIndex{2}\), hence
\[ \cos 104.5° = -0.25\]
and
\[ \gamma = \sqrt{0.25} = 0.5\]
From Equation \(\ref{p}\), then the amount of p character in the hybrid orbitals are
\[ \dfrac{1}{1+\gamma^2} = \dfrac{1}{1+0.5^2} = 0.80\% \]
which leave 20% for s character (Equation \(\ref{s}\)).
\[ \dfrac{\gamma^2}{1+\gamma^2} = \dfrac{0.5^2}{1+0.5^ 2} = 0.20 \]
The two hybridized atomic orbitals of oxygen involved in bonding are each 80% p and 20% s character. This are not perfect \(sp^3\) hybrid orbitals, as expected. Actually, the orbitals involved in the bonds would be better described as \(sp^4\) hybridized. It does not mean that there are 4 p-orbitals in the hybrid orbital, but that each hybrid consists of 20% of s and 80% of p atomic orbitals.
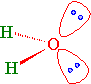
Lone Pairs
Water has two sets of non-bonding electron pairs (Figure \(\PageIndex{4}\)). Without a bond angle to start from, we cannot derive \(\gamma\) that describes the nonbonding hybrid orbitals that they occupy. However, we do know that the O atom has three \(p\) orbitals. So the TOTAL absolute p-character in all hybrid orbitals must be 3.
Let \(x\) be the p-character in the lone pairs hybrid orbitals:
\[0.8 + 0.8 + x + x = 3 \]
This is assuming the lone pairs are identical. Solving for this, x = 0.7 ( i.e. 70% p and 30% s ). From this we can estimate the angle between the lone pair using Equations \(\ref{p}\) and \(\ref{angle}\)
- p-character:
\[\dfrac{1}{1 +\gamma^2} = 0.7\]
so
\[-\gamma^2 = \dfrac{1}{0.7 -1} =-0.42\]
and \(\theta = 115° \).
The angle between the lone pairs is greater (115°) than the bond angle (104.5°). The \(sp^3\) hybrid atomic orbitals of the lone pairs have > 25% s-character. These hybrid orbitals are less directional and held more tightly to the O atom. The \(sp^3\) hybrid atomic orbitals of the bonding pairs have < 25% s-character. They are more directional (i.e., more p-character) and electron density found in the bonding region between O and H.
It should be noted that the valence bond theory application described above predicts that the two lone electron pairs are in the same hybrid orbitals and hence have the same energies. As discussed in the next sections, that is not experimentally observed in photoelectron spectroscopy, which is a shortcoming of valence bond theory's application to water.
Contributors
- Andrew Wolff (

