9.15: Molecular Term Symbols Designate Symmetry

The quantum numbers for diatomic molecules are similar from the atomic quantum numbers. Be cautious, because the rules for finding the possible combinations are different. The total orbital angular momentum quantum number For the molecular case, this number is called \(Λ\) instead of \(L\). It follows the same naming convention as \(L\), except that instead of using capital English letters, it uses capital Greek letters:

• \(Λ = 0 \rightarrow Σ \)
• \(Λ = 1 \rightarrow Π\)
• \(Λ = 2 \rightarrow Δ \)
• \(Λ = 3 \rightarrow Φ \)

Unlike \(L\), there is not a general formula for finding the possible combinations of \(Λ\). You have to examine the individual microstates. This is easier than it sounds.

• The total magnetic quantum number \(M_L\): \(M_L\) works like \(M_l\) with atoms, except that there is no formula for finding the combinations.
• The total spin magnetic quantum number \(M_S\): \(M_S\) works exactly like \(M_s\). Electrons can either point with or against the z ‐ axis, and being in a molecular orbital versus an atomic orbital doesn’t change this. \(M_S\) can range from \(m_{s1} + m_{s2}\) to \(m_{s1} ‐ m_{s2}\).

Two new components: parity and reflection

Molecular orbitals are more complex than atomic ones and require more modifiers to completely define. Parity (sometimes called “inversion”) tells you if the orbital is symmetric or anti‐symmetric when an inversion operation is performed. The symmetry notation u and g are sometimes used when describing molecular orbitals. This refers to the operation of inversion, which requires starting at an arbitrary point in the orbital, traveling straight through the center, and then continuing outwards an equal distance from the center. The orbital is designated g (for gerade, even) if the phase is the same, and u (for ungerade, uneven) if the phase changes sign.

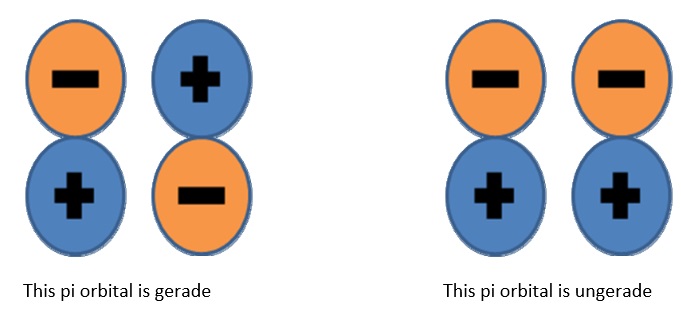
To determine whether or not a given state is \(g\) or \(u\), find the parity of each individual open‐shell electron and uses these simple (Laporte rules):

• \(g + g \rightarrow g \)
• \(g + u \rightarrow u \)
• \(u + u \rightarrow g \)

Example 9.15.1: Closed Shell Configuration

What is the parity of the state \(1σ_g^21σ_u^22σ_g^22σ_u^22π_u^12π_u^1\) ?

Solution

Since both open shell electrons are ungerade, the overall parity is g. Helpful hint: bonding sigma orbitals and anti ‐ bonding pi orbitals are always gerade. Anti ‐ bonding sigmas and bonding pis are always ungerade. Draw them and see for yourself.

Reflection determines if a given orbital is symmetric or anti‐symmetric upon reflection through a plane that contains both nuclei. The choice of symmetry planes is arbitrary. As long as you pick a plane and stick with it, you will always get the right answer. When an orbital is symmetric, it is labeled +. When an orbital is anti ‐ symmetric, it is labeled ‐ . To find the overall reflection of a state, use these rules:

• (+)(+) \rightarrow +
• (+)(‐) \rightarrow ‐
• (‐)(‐) \rightarrow +

Reflection only applies to Σ states! For Λ > 0, there are no reflection labels! If you experiment with the rules, you will quickly realize why this is the case.

Example 9.15.2

What is the reflection of the state \(1σ_g^21σ_u^22σ_g^22σ_u^22π_u^12π_u^1\) ?

Solution

You need to know what the orbitals look like. Draw a picture and then pick a plane. For this example, the plane of the page is selcted, but the orthogonal plane would have worked just as well.

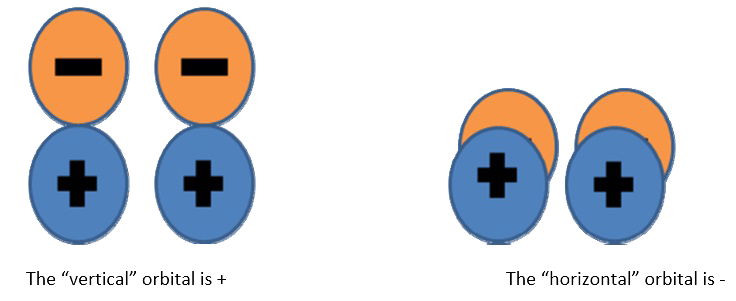
The “vertical” orbital is + The “horizontal” orbital is ‐ Since one is + and one is ‐ , the overall reflection is ‐ . Try using the orthogonal plane and convince yourself that you still get the same answer.

Example 9.15.3: Oxygen

What are the term symbols for \(O_2\) ?

Solution

The molecular orbital diagram for \(O_2\) is

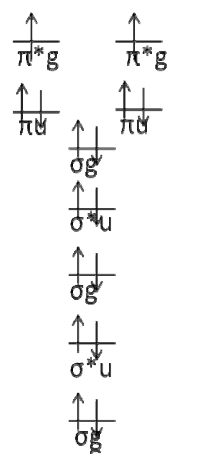
Where I chose arbitrary configurations for the last two electrons.

There are two open ‐ shell electrons occupying the anti‐bonding \(π_g\) orbitals. These are the only electrons that matter. It is easiest to simply draw all of the permutations and figure out the bounds on \(Λ\) and \(M_L\) by inspection. If we do this, it is easy to see that \(Λ = 2,0\) and that \(M_L = 2,0, ‐ 2\)

\(M_s= -1\)	\(M_s= 0\)	\(M_s= 2\)
0	1	0
1	2	1
0	1	0

The top row is a \(Λ=2\) \(M_S =0\) state, so it is \(^1Δ\). Both electrons are in the rightmost orbital. This orbital is gerade, and (g)(g) = g, so the parity label is g. We do not assign reflection labels to non Σ states, so the term symbol is \(^1Δ_g\). After removing the used up microstates, the chart becomes

\(M_s= -1\)	\(M_s= 0\)	\(M_s= 2\)
1	1	0

This is a Λ =0 state with three possible spin configurations, so it is \(^3Σ\). We know that the electrons are in different sub‐orbitals (if you cannot see this, try drawing all of the possible combinations that give \(Λ =0\)). Both of the orbitals are gerade, so the overall parity is gerade. One of the orbitals will be +, the other will be ‐ . The final answer is \(^1Δ_g \(^3Σ^+_g\)

Exercise 9.15.1

Write the term symbols for \(O_2^‐\)

Solution

First draw the electron configuration diagram.

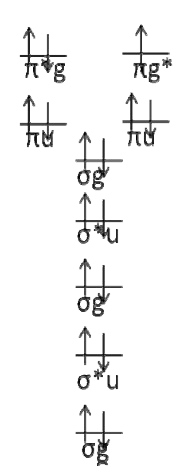
There are only two possible configurations. It should be easy to see that the term symbol is \(^2\Pi_g\).

Contributors

• Mattanjah de Vries (Chemistry, University of California, Santa Barbara)