8.8: Term Symbols Gives a Detailed Description of an Electron Configuration
- Page ID
- 210846
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Conveniently for chemists, an atom’s electronic state depends entirely on its unfilled sub shells. Because electrons distribute themselves in a symmetric manner, the inner shell electrons end up canceling out each other’s momenta. For an atom in the configuration \(1s^2 2s^2 p^2\), only the two p‐electrons matter. For an atom in the configuration \(1s^22s^12p^1\), we have to examine the 2s and 2p electrons. Atoms have quantum numbers that are directly analogous to the electronic quantum numbers.
The Total Orbital Angular Momentum Quantum Number: L
One might naively think that you could get the total angular momentum of an atom by simply adding up the \(l\) values of the individual electrons. The problem with this idea is that the angular momenta of the various electrons are not necessarily pointing in the same direction. If two electrons are revolving in the same direction as each other, you would add their \(l\) values.
\[ L = \sum_i^n l_i \label{8.8.4A}\]
If they were revolving opposite to each other, you would subtract them. If they are revolving at some off ‐ angle relative to each other, you would partially subtract them. To figure out all of the possible combinations of l for a pair of electrons, simply add them together to get the co‐aligned case, subtract them to get the opposing case, and then fill in all the numbers in between to get the off‐angle cases. If you prefer to have a formula, you can use this:
\[L = |l_1 + l_2 | , |l_1 + l_2 ‐ 1| , \ldots, |l_1 ‐ l_2 | \label{8.8.5A}\]
What are the possible \(L\) values for the electrons in the \(1s^2 2s^2 2p^2\) configuration of carbon?
Solution
Both open‐shell electrons (i.e., the 2p electrons) are \(l = 1\). The possible combinations are 2, 1, 0.
What are the possible \(L\) values for the electrons in the \([Xe]6s^2 4f^1 5d^1\) ?
Solution
We have an \(l=3\) and an \(l=2\) electron.
\[3+2 = 5\]
and
\[3 ‐ 2 = 1\]
The possible combinations are 5, 4, 3, 2, 1
The Total Magnetic Quantum Number: \(M_l\)
\(M_l\) is the total z‐component of all of the relevant electrons’ orbital momentum. Where \(L\) told you how much angular momentum there was, \(M_l\) tells you which direction it is pointing. Like \(L\), a given configuration can have several possible values of \(M_l\), depending on the electrons’ relative orientation. Unlike \(L\), \(M_l\) is allowed to have negative values. To list the possible \(M_l\) values for a two electron system, take the case where both \(m_l\) are positive, then take the case where they are both negative, and then fill in the numbers in between.
\[M_l = m_{l1} + m_{l2}, m_{l1} + m_{l2} ‐ 1, ... , ‐m_{l1} ‐ m_{l2} \label{8.8.6}\]
What are the possible values \(M_l\) of a zirconium atom with the \([Kr] 5s^2 4d^2\) electron configuration?
Solution
Both open‐shell electrons (i.e., the 4d electrons) are \(l=2\), so the values are 4, 3, 2, 1, 0, ‐1, ‐2, ‐3, ‐4.
The Total Spin Magnetic Quantum Number: \(M_s\)
\(M_s\) is the sum total of the z‐components of the electrons’ inherent spin. Do not confuse it with \(M_l\), which is the sum total of the z‐component of the orbital angular momentum. It is easily computed by finding all of the possible combinations of \(m_s\). Since \(m_s\) for each individual electron can only be +1/2 or ‐ 1/2, this isn’t too complicated.
\[M_s = m_{s1} + m_{s2}, m_{s1} +m_{s2} ‐ 1 , ... , m_{s1} ‐ m_{s2} \label{8.8.7}\]
What are the M s values for \(1s^2 2s^2 2p^2\) ?
Solution
\(M_s = 1, 0, ‐1\)
The Total Intrinsic Spin Quantum Number: \(S\)
The sum total of the spin vectors of all of the electrons is called \(S\). The difference between \(S\) and \(M_s\) is subtle, but vital for understanding multiplicity. \(M_s\) measures the total z‐component of the electrons’ spins, while \(S\) measures the entire resultant vector. The values of \(S\) are computing in a manner very similar to \(M_s\). Because \(S\) measures the magnitude of a vector, it cannot ever be negative.
\[S = |s_1 + s_2 |, |s_1 +s_2 ‐ 1| , ... ,| s_1 ‐ s_2 | \label{8.8.8}\]
Find \(S\) for \(1s^1\).
Solution
\(S\) clearly has to be ½ since that’s the spin of a single electron and there’s only one electron to worry about.
Find S for \(1s^2 2s^1 2p^1\).
Solution
\(S = 1, 0\)
Find \(S\) for carbon atoms with the \(1s^2 2s^2 2p^2\) electron configuration.
Solution
\(S=1,0\) This is the same as the previous problem. Notice that \(S\) is not affected by which orbitals the electrons are in. \(S\) only cares about how many open‐shell electrons (i.e., unpaired electrons) there are, not about where they are. This is because \(S\) measures an inherent property of the electrons themselves
Find \(S\) for nitrogen atoms with the \(1s^2 2s^2 2p^3\) electron configuration.
Solution
We have not done a three electron case yet, but they are not hard. Find all the combinations for a single pair first, and then factor in the third electron. For two electrons, we already know that the two possible S values are S=1,0. A third electron can either add or subtract ½ from these values, so the final \(S\) can be \(S=3/2, 1, 1/2\).
The Total Angular Momentum Quantum Number J
The total orbital angular momentum of an atom (measured in terms of \(L\)), and the total spin angular momentum of an atom (measure in \(S\)) combine to form total angular momentum, a number that is quantized by the number \(J\). \(L\) and do not necessarily have to be pointing in the same direction (Figure \(\PageIndex{1}\)), so \(J\) can range from \(L + S\) to \(|L – S|\).

| Symbol | Name | Allowed Range |
|---|---|---|
| \(L\) | Total orbital angular momentum | \(|l_1 + l_2 |, ..., |l_1 ‐ l_2 |\) |
| \(M_l\) | Magnet Quantum number | \( [m_{l1} + m_{l2}, ..., ‐ m_{l1} ‐ m_{l2} ]\) |
| \(M_s\) | Spin Magnetic Quantum Number | \( | m_{s1} + m_{s2} |,..., |m_{s1} ‐ m_{s2} | \) |
| \(S\) | Inherent Spin Number | \(|s_1 + s_2 |,..., |s_1 ‐ s_2 |\) |
| \(M\) | Multiplicity | 2S+1 |
| \(J\) | Total Angular Momentum | \(L+S,..., | L-S |\) |
Multiplicity
Multiplicity is a simple ‐ sounding concept that defies simple explanations. You know from your first ‐ year education that a singlet is when the net spin (S) is equal to zero (e.g. all the electrons are spin paired), and a triplet happens when the net spin is equal to 1 (e.g. two electrons are pointing in the same direction). They are called “singlet” and “triplet” because there are 3 ways to combine a pair of electron spins to get S=1, but only one way to get \(S=0\). If you draw a picture of the possible ways that two electrons can arrange their spins, you get something like this:
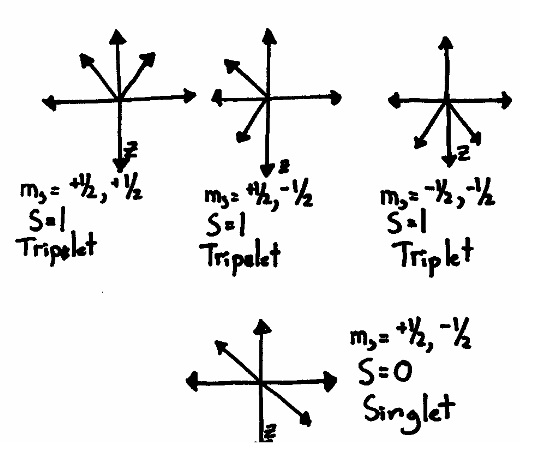
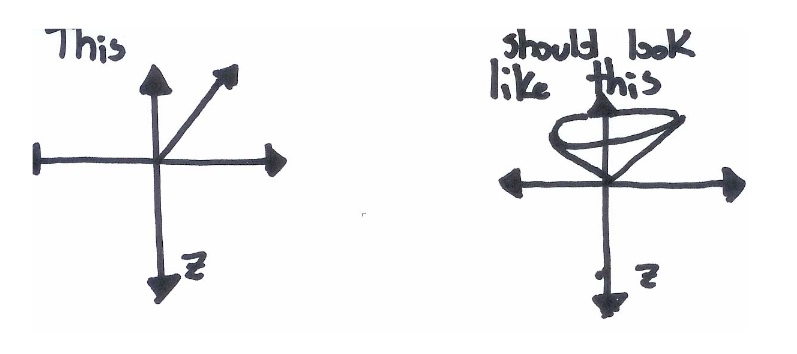
While this picture is an improvement over the simple up‐down model, it is still misleading. The three spin axes of an electron share a Heisenberg Uncertainty Principle. The more you know about \(S_x\), the less you can know about either \(S_y\) or \(S_z\). The same is true for all other combinations of x, y and z. Since we have defined \(S_z\) as a known and fixed value, the values of \(S_x\) and \(S_y\) must be completely unknown. This causes the x and y orientations of the electrons to become smeared out across all possible values:
Constructing Term Symbols
Atomic term symbols contain two pieces of information. They tell you the total orbital angular momentum of the atom (\(L\)), and they tell you the multiplicity (\(M\)). \(L\) is denoted by a simple code, similar to the code used to delineate the types of atomic orbitals:
- \(L=0 \rightarrow S \)
- \(L=1 \rightarrow P\)
- \(L=2 \rightarrow D\)
- \(L=3 \rightarrow F\)
Note that while the notation is similar, L does NOT say anything about what types of orbitals the electrons are in. A state that has the term symbol P does NOT necessarily have an open p‐shell. The multiplicity is indicated by appending a number to the upper left of the symbol. A \(L=2\), \(M=3\) state would be represented by \(^3D\). The secret to writing the term symbols for an atom is to discover what combinations of \(L\) and \(M\) are possible for that atom with that specific electronic configuration. An atom that only has closed shells will always be \(1S\).
Each term symbol represents a discrete energy level. We can place these levels in the correct order by using these simple rules:
- 1: High multiplicity values mean low energy
- 2: If there is a tie, high \(L\) values mean low energy
- 3a: If there is still a tie and the shell is less than half full, then low J means low energy
- 3b: If the shell is more than half full, then high J means low energy
These rules reliably predict the ground state. They have only erratic agreement with experiment when ordering the other levels.
What are the term symbols for the microstates possible for \(1s^1\) electronic configuration of hydrogen?
Solution
Since there is only one electron, this is a simple problem. \(L=0\) and \(M=1\), so the only possible term symbol is \(^2S\). With only one electron, \(S = ½\), so \(J = 0 + ½ = ½\). Only one microstate exists for this configuration and it has a term symbol of \(^2S_{½}\).
What are the term symbols for the microstates possible for \(1s^2 2s^2 2p^1\) electronic configuration of boron?
Solution
There still only one open shell electron, so \(L=1\), \(M=1\) and \(S = ½\). We get a term symbol of the type \(^2P\), which gets split into separate symbols because \(J = 3/2\) and \(1/2\). Two possible microstates exist for this system with term symbols of \(^2P_{3/2}\) and \(^2P_{1/2}\).
What are the term symbols for the microstates possible for the \(1s^2 2s^1 2p^1\) excited-state electronic configuration of Beryllium?
Solution
Now we have two electrons to worry about. Since \(l_1 = 0\) and \(l_2 = 1\), the only possible combination is \(L=1\). The possible combinations of S are: \(S=1,0\). This means that \(M=3\) or \(M=1\). The term symbols will be of the form \(^1P\) and \(^3P\). For the \(^1 P\) state, \(L=1\) and \(S=0\), so \(J=1\). For the second state, \(L=1\) and \(S=1\), so \(J=2,1,0\). There are four microstates for this configuration with term symbols of \(^1 P_1\) and \(^3 P_2\), \(^3P_1\), and \(^3P_0\).
What are the term symbols for the microstates possible for the \([Kr] 5s^2 4d^2\) ground-state electronic configuration of zirconium?
Solution
This is a much harder problem. We will need to use a special technique to disentangle all of the possible combinations of \(L\) and \(M\). Let’s start be listing the relevant quantum numbers for the two open-shell electrons:
|
\(l_1 = 2\) |
\(l_2 = 2\) |
| \(m_{l1} = 2, 1, 0, ‐ 1, ‐ 2\) | \(m_{l2} = 2, 1, 0, ‐ 1, ‐ 2\) |
| \(m_{s1} = ½, ‐½\) | \(m_{s1} = ½, ‐½\) |
Let’s combine these numbers to generate the atomic quantum numbers:
\[L = 4,3,2,1,0 \]
\[M_l = 4,3,2,1,0, ‐ 1, ‐ 2, ‐ 3, ‐ 4\]
\[M_s = 1,0\]
We know that there will at least one each of S, P, D, F and G. It isn’t immediately clear which of these will be singlets and which will be triplets. To figure this out, we need to systematically examine the possible microstates. It turns out that there are 45 possible ways to put distribute two electrons between 5 d orbitals. That’s a lot! The easiest way to list the states is to organize them into a chart:
| \(M_s= -1\) | \(M_s= 0\) | \(M_s= +1\) |
|---|---|---|
Attacking the chart one row at a time. Ask yourself, how many ways can I arrange the two electrons to give me \(M_l = 4\)? It turns out there is only one possible combination that does this:
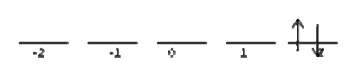
This state is has \(M_s = 0\). This means that there is only 1 microstate that corresponds to \(M_l =4\) and \(M_s = 0\), and none that correspond to \(M_l =4\) and \(M_s = \pm ‐1\). We add this microstate to the chart like this:
| \(M_l\) | \(M_s= -1\) | \(M_s= 0\) | \(M_s= +1\) |
|---|---|---|---|
| 4 | 0 | 1 | 0 |
Now, how many ways are there to get \(M_l = 3\)?
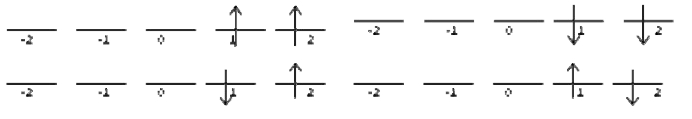
| \(M_l\) | \(M_s= -1\) | \(M_s= 0\) | \(M_s= +1\) |
|---|---|---|---|
| 4 | 0 | 1 | 0 |
| 3 | 1 | 2 | 1 |
For \(M_l =2\), we find the following states:
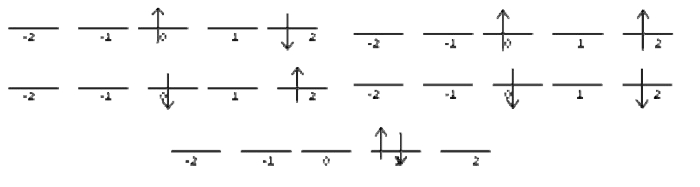
| \(M_l\) | \(M_s= -1\) | \(M_s= 0\) | \(M_s= +1\) |
|---|---|---|---|
| 4 | 0 | 1 | 0 |
| 3 | 1 | 2 | 1 |
| 2 | 1 | 3 | 1 |
You should be able to draw the microstates on your own by now. You should find 8 states, four of which are singlet and four of which are triplets.
| \(M_l\) | \(M_s= -1\) | \(M_s= 0\) | \(M_s= +1\) |
|---|---|---|---|
| 4 | 0 | 1 | 0 |
| 3 | 1 | 2 | 1 |
| 2 | 1 | 3 | 1 |
| 1 | 2 | 4 | 2 |
There are only nine possible ways to arrange the electrons to get \(M_l =0\)
| \(M_l\) | \(M_s= -1\) | \(M_s= 0\) | \(M_s= +1\) |
|---|---|---|---|
| 4 | 0 | 1 | 0 |
| 3 | 1 | 2 | 1 |
| 2 | 1 | 3 | 1 |
| 1 | 2 | 4 | 2 |
| 0 | 2 | 5 | 2 |
The rest of the chart will be symmetric to the first half, so we do not need to do any more work:
| \(M_l\) | \(M_s= -1\) | \(M_s= 0\) | \(M_s= +1\) |
|---|---|---|---|
| 4 | 0 | 1 | 0 |
| 3 | 1 | 2 | 1 |
| 2 | 1 | 3 | 1 |
| 1 | 2 | 4 | 2 |
| 0 | 2 | 5 | 2 |
| -1 | 2 | 4 | 2 |
| -2 | 1 | 3 | 1 |
| -3 | 1 | 2 | 1 |
| -4 | 0 | 1 | 0 |
Now that we have a listing of all of the microstates, we need to figure out how to divide them up between the term symbols. It turns out that each term symbol can have, at most, one microstate from each box on the chart. The term symbols always end up claiming a “box” of microstates, centered on the middle of the chart. This is easier shown than said.
Attacking the chart from the top, we can see that the \(M_l = 4\) \(M_s = 0\) state clearly belongs to a \(^1G\) symbol. The \(M_l = ‐4\) \(M_s =0\) box also clearly belongs to this symbol. If I connect these states with a “box,” I get this:
| \(M_l\) | \(M_s= -1\) | \(M_s= 0\) | \(M_s= +1\) |
|---|---|---|---|
| 3 | 1 | 2 | 1 |
| 2 | 1 | 3 | 1 |
| 1 | 2 | 4 | 2 |
| 0 | 2 | 5 | 2 |
| -1 | 2 | 4 | 2 |
| -2 | 1 | 3 | 1 |
| -3 | 1 | 2 | 1 |
The strickthough configurations all belong to the \(^1 G\) state. Let's subtract them from the chart to indicate that they are not available for other term symbols.
| \(M_l\) | \(M_s= -1\) | \(M_s= 0\) | \(M_s= +1\) |
|---|---|---|---|
| 3 | 1 | 2 | 1 |
| 2 | 1 | 3 | 1 |
| 1 | 2 | 4 | 2 |
| 0 | 2 | 5 | 2 |
| -1 | 2 | 4 | 2 |
| -2 | 1 | 3 | 1 |
| -3 | 1 | 2 | 1 |
The next row indicates a \(L=3\) state. Because there are three \(M_s\) values available, this is a triplet. The term symbol will be \(^3F\), which reduces the chart down to
| \(M_l\) | \(M_s= -1\) | \(M_s= 0\) | \(M_s= +1\) |
|---|---|---|---|
| 1 | 2 | 4 | 2 |
| 0 | 2 | 5 | 2 |
| -1 | 2 | 4 | 2 |
The next state will be \(^1D\). Leaving us with
| \(M_l\) | \(M_s= -1\) | \(M_s= 0\) | \(M_s= +1\) |
|---|---|---|---|
| 1 | 1 | 1 | 1 |
| 0 | 1 | 2 | 1 |
| -1 | 1 | 1 | 1 |
Next is a \(^3P\) state. The chart is getting pretty small now wtih
| \(M_l\) | \(M_s= 0\) |
|---|---|
| 0 |
The last remaining microstate comprises the \(^1S\) term symbol.
The total listing is
\(^1G\), \(^3F\), \(^1D\), \(^3P\), \(^1S\).
Assigning \(J\) values, we get
\(^1G_4\), \(^3F_4\), \(^3F_3\), \(^3F_2\), \(^1D_2\), \(^3P_2\), \(^3P_1\), \(^3P_0\), \(^1S_0\)
If you can do this problem, you can do almost any atomic term symbol.
The secret to writing the term symbols for an atom is to discover what combinations of \(L\) and \(M\) are possible for that atom with that specific electronic configuration.
Shortcuts
There is a deep symmetry that connects different electronic configurations. It turns out that a \(p^1\) configuration has the same term symbols as a \(p^5\). Similarly, \(p^2 = p^4\). A similar relationship can be used to figure out high electron number term symbols for the \(d\) and \(f\) orbitals.
Contributors
Mattanjah de Vries (Chemistry, University of California, Santa Barbara)

