6.10: Collisions between Gas Molecules Relative Velocity Coordinates
- Last updated
- Save as PDF
- Page ID
- 206349
The pressure of a gas depends on the frequency with which molecules collide with the wall of their container. The rate at which gas molecules escape through a very small opening in their container is called the effusion rate. The effusion rate rate also depends on the frequency of collisions with the wall. (See problem 4.12.) Other gas properties depend not on the rate of collision with the wall, but on the rate with which gas molecules collide with one another. We turn now to some of these properties. For these considerations, we need to describe the motion of one molecule relative to another. We need the probability density function for the relative velocity of two particles.
To describe the relative velocity of two particles, we introduce relative velocity coordinates. Let us begin by considering a Cartesian coordinate frame, with \(x\)-, \(y\)-, and z-axes, whose origin is at a point \(O\); we will use \(Oxyz\) to designate this set of axes. We specify the location of particle \(1\) by the vector \({\mathop{r}\limits^{\rightharpoonup}}_1=\left(x_1,y_1,z_1\right)=x_1\mathop{i}\limits^{\rightharpoonup}+y_1\mathop{j}\limits^{\rightharpoonup}+z_1\mathop{k}\limits^{\rightharpoonup}\) and that of particle \(2\) by \({\mathop{r}\limits^{\rightharpoonup}}_2=\left(x_2,y_2,z_2\right)\). We let the location of the center of mass of this two-particle
system be specified by \({\mathop{r}\limits^{\rightharpoonup}}_0=\left(x_0,y_0,z_0\right)\). The vector from particle \(1\) to particle \(2\), \({\mathop{r}\limits^{\rightharpoonup}}_{12}=\left(x_{12},y_{12},z_{12}\right)\), is the vector difference
\[{\mathop{r}\limits^{\rightharpoonup}}_{12}={\mathop{r}\limits^{\rightharpoonup}}_2-{\mathop{r}\limits^{\rightharpoonup}}_1=\left(x_2-x_1,y_2-y_1,z_2-z_1\right)\nonumber \]
When the particles are moving, these vectors and their components are functions of time. Using the notation \({\dot{x}}_1={dx_1}/{dt}\), we can specify the velocity of particle \(1\), for example, as \({\mathop{v}\limits^{\rightharpoonup}}_1={d{\mathop{r}\limits^{\rightharpoonup}}_1}/{dt}=\left({\dot{x}}_1,{\dot{y}}_1,{\dot{z}}_1\right)\). Our goal is to find the relative velocity vector, \({\mathop{v}\limits^{\rightharpoonup}}_{12}={d{\mathop{r}\limits^{\rightharpoonup}}_{12}}/{dt}\). We call the components of \({\mathop{v}\limits^{\rightharpoonup}}_{12}\) the relative velocity coordinates.
The essential idea underlying relative velocity coordinates is that the vectors \({\mathop{r}\limits^{\rightharpoonup}}_0\) and \({\mathop{r}\limits^{\rightharpoonup}}_{12}\) contain the same information as the vectors \({\mathop{r}\limits^{\rightharpoonup}}_1\) and \({\mathop{r}\limits^{\rightharpoonup}}_2\). This is equivalent to saying that we can transform the locations as specified by \(\left(x_1,y_1,z_1\right)\) and \(\left(x_2,y_2,z_2\right)\) to the same locations as specified by \(\left(x_0,y_0,z_0\right)\) and \(\left(x_{12},y_{12},z_{12}\right)\), and vice versa. To accomplish this, we write the equation defining the \(x\)-component of the center of mass, \(x_0\):
\[m_1\left(x_1-x_0\right)+m_2\left(x_2-x_0\right)=0\nonumber \]
which we rearrange to
\[\frac{x_1}{m_2}+\frac{x_2}{m_1}=\left(\frac{1}{m_1}+\frac{1}{m_2}\right)x_0\nonumber \]
Corresponding relationships can be written for the \(y\)- and \(z\)-components. It proves to be useful to introduce the reduced mass, \(\mu\), defined by
\[\frac{1}\mu=\frac{1}{m_1}+\frac{1}{m_2}\nonumber \]
Using the reduced mass, we can express the coordinates of the center of mass in terms of the coordinates of the individual particles. That is,
\[x_0=\left(\frac\mu{m_2}\right)x_1+\left(\frac\mu{m_1}\right)x_2\nonumber \]
\[y_0=\left(\frac\mu{m_2}\right)y_1+\left(\frac\mu{m_1}\right)y_2\nonumber \]
\[z_0=\left(\frac\mu{m_2}\right)z_1+\left(\frac\mu{m_1}\right)z_2\nonumber \]
Since, by definition, we also have
\[x_{12}=x_2-x_1\nonumber \] \[y_{12}=y_2-y_1\nonumber \] \[z_{12}=z_2-z_1\nonumber \]
we have developed the transformation from \(\left(x_0,y_0,z_0\right)\) and \(\left(x_{12},y_{12},z_{12}\right)\) to \(\left(x_1,y_1,z_1\right)\) and \(\left(x_2,y_2,z_2\right)\). The inverse transformation is readily found to be
\[x_1=x_0-\left(\mu/{m_1}\right)x_{12}\nonumber \]
\[y_1=y_0-\left(\mu/{m_1}\right)y_{12}\nonumber \]
\[z_1=z_0-\left(\mu/{m_1}\right)z_{12}\nonumber \]
\[x_2=x_0+\left(\mu/{m_2}\right)x_{12}\nonumber \]
\[y_2=y_0+\left(\mu/{m_2}\right)y_{12}\nonumber \]
\[z_2=z_0+\left(\mu/{m_2}\right)z_{12}\nonumber \]
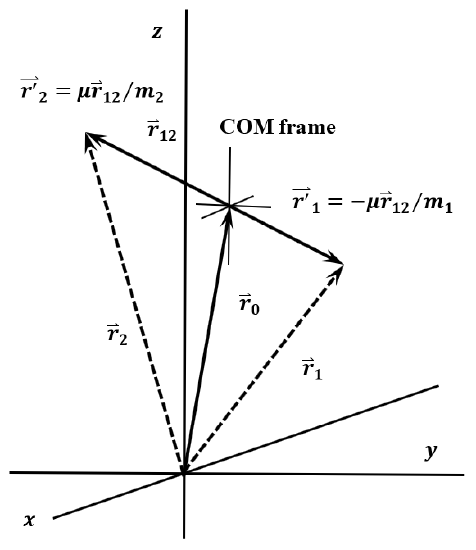
Now we can create two new Cartesian coordinate frames. Which of these is more useful depends on the objective of the particular analysis we have at hand. We call the first one the center of mass frame, \(O_Ox^{'}y^{'}z^{'}\). It is sketched in Figure 7. The \(x{'}\)-, \(y{'}\)-, and \(z{'}\)-axes of \(O_Ox^{'}y^{'}z^{'}\) are parallel to the corresponding axes of \(Oxyz\), but their origin, \(O_O\), is always at the point occupied by the center of mass of the two-particle system. In this reference frame, the coordinates of particles \(1\) and \(2\) are their displacements from the center of mass:
\[x^{'}_1=x_1-x_0=-\left(\mu/{m_1}\right)x_{12}\nonumber \]
\[y^{'}_1=y_1-y_0=-\left(\mu/{m_1}\right)y_{12}\nonumber \]
\[z^{'}_1=z_1-z_0=-\left(\mu/{m_1}\right)z_{12}\nonumber \]
\[x^{'}_2=x_2-x_0=\left(\mu/{m_2}\right)x_{12}\nonumber \]
\[y^{'}_2=y_2-y_0=\left(\mu/{m_2}\right)y_{12}\nonumber \]
\[z^{'}_2=z_2-z_0=\left(\mu/{m_2}\right)z_{12}\nonumber \]
The center of mass frame is particularly useful for analyzing interactions between colliding particles.
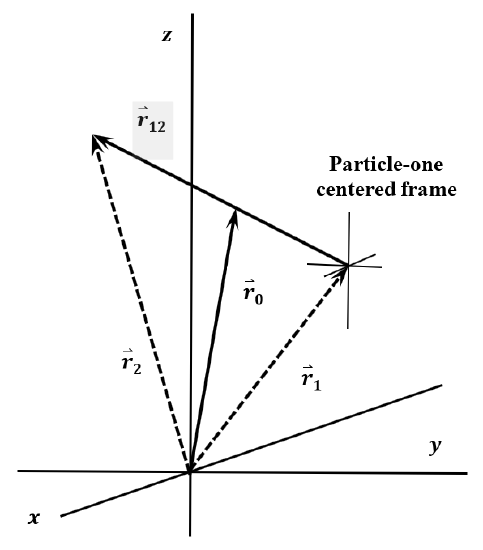
For our purposes, a third Cartesian coordinate frame, which we will denote the \(O_1x^{''}y^{''}z^{''}\) frame, is more useful. It is sketched in Figure 8. The \(x^{''}\)-, \(y^{''}\)-, and \(z^{''}\)-axes of \(O_1x^{''}y^{''}z^{''}\) are parallel to the corresponding axes of \(Oxyz\), but their origin, \(O_1\), is always at the point occupied by particle 1. In this reference frame, the coordinates of particles 1 and 2 are
\[x^{''}_1=0\nonumber \]
\[y^{''}_1=0\nonumber \]
\[z^{''}_1=0\nonumber \]
\[x^{''}_2=x_2-x_1=x_{12}\nonumber \]
\[y^{''}_2=y_2-y_1=y_{12}\nonumber \]
\[z^{''}_2=z_2-z_1=z_{12}\nonumber \]
and the coordinates of the center of mass are
\[x^{''}_0=x_0-x_1={\mu x_{12}}/{m_1}\nonumber \]
\[y^{''}_0=y_0-y_1={\mu y_{12}}/{m_1}\nonumber \]
\[z^{''}_0=z_0-z_1={\mu z_{12}}/{m_1}\nonumber \]
The \(O_1x^{''}y^{''}z^{''}\) frame is sometimes called the center of mass frame also. To avoid confusion, we call \(O_1x^{''}y^{''}z^{''}\) the particle-one centered frame. In the particle-one centered frame, particle \(1\) is stationary at the origin. With its tail at the origin, the vector \({\mathop{r}\limits^{\rightharpoonup}}_{12}=\left(x_{12},y_{12},z_{12}\right)\) specifies the position of particle \(2\).
We are interested in the relative velocity of particles \(1\) and \(2\). The velocity components for particles \(1\) and \(2\), and for their relative velocity, are obtained by finding the time-derivatives of the corresponding displacement components. Since the transformations of the displacement coordinates are linear, the velocity components transform from one reference frame to another in exactly the same way that the displacement components do. We have
\[{\mathop{v}\limits^{\rightharpoonup}}_0={d{\mathop{r}\limits^{\rightharpoonup}}_0}/{dt}=\left({\dot{x}}_0,{\dot{y}}_0,{\dot{z}}_0\right)\nonumber \]
and
\[{\mathop{v}\limits^{\rightharpoonup}}_{12}={d{\mathop{r}\limits^{\rightharpoonup}}_{12}}/{dt}=\left({\dot{x}}_{12},{\dot{y}}_{12},{\dot{z}}_{12}\right)\nonumber \]
The vector \({\mathop{v}\limits^{\rightharpoonup}}_{12}\) specifies the velocity of particle \(2\), relative to a stationary particle \(1\). Just as \({\mathop{r}\limits^{\rightharpoonup}}_0\) and \({\mathop{r}\limits^{\rightharpoonup}}_{12}\) contain the same information as the vectors \({\mathop{r}\limits^{\rightharpoonup}}_1\) and \({\mathop{r}\limits^{\rightharpoonup}}_2\), the vectors \({\mathop{v}\limits^{\rightharpoonup}}_0\) and \({\mathop{v}\limits^{\rightharpoonup}}_{12}\) contain the same information as \({\mathop{v}\limits^{\rightharpoonup}}_1\) and \({\mathop{v}\limits^{\rightharpoonup}}_2\). Since a parallel displacement leaves a vector unchanged, each of these vectors is the same in any of the three reference frames. In §11, we find the probability density function for the magnitude of the scalar relative velocity, \(v_{12}=\left|{\mathop{v}\limits^{\rightharpoonup}}_{12}\right|\). Since the probability is independent of direction, the probability that two molecules have relative velocity \({\mathop{v}\limits^{\rightharpoonup}}_{12}\) is the same as that they have relative velocity \({-\mathop{v}\limits^{\rightharpoonup}}_{12}\). (In spherical coordinates, if \({\mathop{v}\limits^{\rightharpoonup}}_{12}=\left(v_{12},\theta ,\varphi \right)\), then \(-{\mathop{v}\limits^{\rightharpoonup}}_{12}=\left(v_{12},\theta +\pi ,\varphi +\pi \right)\).) The probability and magnitude of the relative velocity are independent of which particle—if either—we choose to view as being stationary; they are independent of whether the particles are approaching or receding from one another.


