Skip to main content
Chemistry LibreTexts

4.4: Formula Mass, Percent Composition, and the Mole

  1. Last updated
  2. Save as PDF
  • Page ID
    217263

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

    ( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\id}{\mathrm{id}}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\kernel}{\mathrm{null}\,}\)

    \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\)

    \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\)

    \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    \( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

    \( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

    \( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vectorC}[1]{\textbf{#1}} \)

    \( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

    \( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

    \( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)

    Skills to Develop

    • Calculate formula masses for covalent and ionic compounds
    • Define the amount unit mole and the related quantity Avogadro’s number
    • Explain the relation between mass, moles, and numbers of atoms or molecules, and perform calculations deriving these quantities from one another
    • Compute the percent composition of a compound

    We can argue that modern chemical science began when scientists started exploring the quantitative as well as the qualitative aspects of chemistry. For example, Dalton’s atomic theory was an attempt to explain the results of measurements that allowed him to calculate the relative masses of elements combined in various compounds. Understanding the relationship between the masses of atoms and the chemical formulas of compounds allows us to quantitatively describe the composition of substances.

    Formula Mass

    In an earlier chapter, we described the development of the atomic mass unit, the concept of average atomic masses, and the use of chemical formulas to represent the elemental makeup of substances. These ideas can be extended to calculate the formula mass of a substance by summing the average atomic masses of all the atoms represented in the substance’s formula.

    Formula Mass for Covalent Substances

    For covalent substances, the formula represents the numbers and types of atoms composing a single molecule of the substance; therefore, the formula mass may be correctly referred to as a molecular mass. Consider chloroform (CHCl3), a covalent compound once used as a surgical anesthetic and now primarily used in the production of tetrafluoroethylene, the building block for the “anti-stick” polymer, Teflon. The molecular formula of chloroform indicates that a single molecule contains one carbon atom, one hydrogen atom, and three chlorine atoms. The average molecular mass of a chloroform molecule is therefore equal to the sum of the average atomic masses of these atoms. Figure \(\PageIndex{1}\) outlines the calculations used to derive the molecular mass of chloroform, which is 119.37 amu.

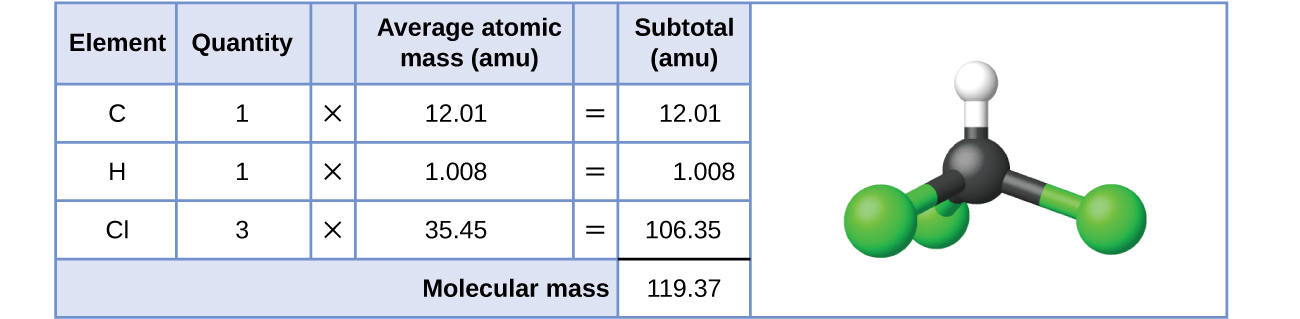
    A table and diagram are shown. The table is made up of six columns and five rows. The header row reads: “Element,” “Quantity,” a blank space, “Average atomic mass (a m u),” a blank space, and “Subtotal (a m u).” The first column contains the symbols “C,” “H,” “C l” and a blank, merged cell that runs the width of the first five columns. The second column contains the numbers “1,” “1,” and “3” as well as the merged cell. The third column contains the multiplication symbol in each cell except for the last, merged cell. The fourth column contains the numbers “12.01,” “1.008,” and “35.45” as well as the merged cell. The fifth column contains the symbol “=” in each cell except for the last, merged cell. The sixth column contains the values “12.01,” “1.008,” “106.35,” and “119.37.” There is a thick black line below the number 106.35. The merged cell under the first five columns reads “Molecular mass.” To the left of the table is a diagram of a molecule. Three green spheres are attached to a slightly smaller black sphere, which is also attached to a smaller white sphere. The green spheres lie beneath and to the sides of the black sphere while the white sphere is located straight up from the black sphere.

    Figure \(\PageIndex{1}\): The average mass of a chloroform molecule, CHCl3, is 119.37 amu, which is the sum of the average atomic masses of each of its constituent atoms. The model shows the molecular structure of chloroform.

    Likewise, the molecular mass of an aspirin molecule, C9H8O4, is the sum of the atomic masses of nine carbon atoms, eight hydrogen atoms, and four oxygen atoms, which amounts to 180.15 amu (Figure \(\PageIndex{2}\)).

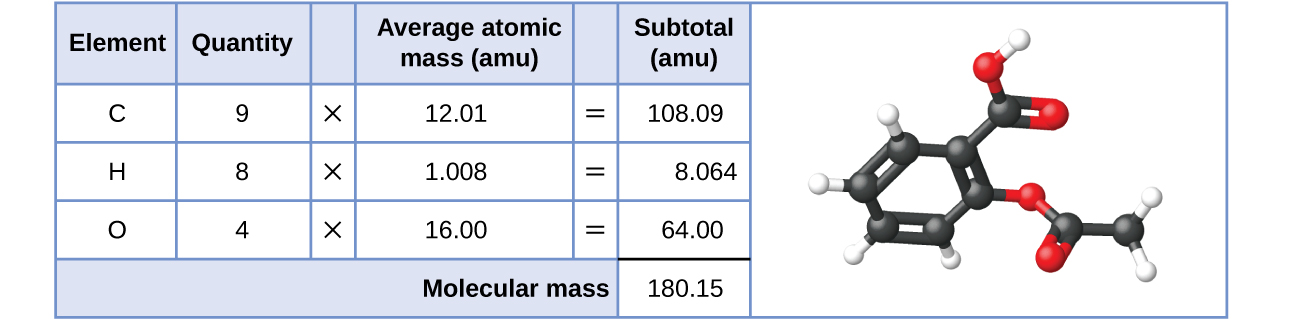
    A table and diagram are shown. The table is made up of six columns and five rows. The header row reads: “Element,” “Quantity,” a blank space, “Average atomic mass (a m u),” a blank space, and “Subtotal (a m u).” The first column contains the symbols “C,” “H,” “O,” and a merged cell. The merged cell runs the length of the first five columns. The second column contains the numbers “9,” “8,” and “4” as well as the merged, cell. The third column contains the multiplication symbol in each cell except for the last, merged cell. The fourth column contains the numbers “12.01,” “1.008,” and “16.00” as well as the merged cell. The fifth column contains the symbol “=” in each cell except for the last, merged cell. The sixth column contains the values: “108.09,” “8.064,” “64.00,” and “180.15.” There is a thick black line below the number 64.00. The merged cell under the first five columns reads “Molecular mass.” To the left of the table is a diagram of a molecule. Six black spheres are located in a six-sided ring and connected by alternating double and single black bonds. Attached to each of the four black spheres is one smaller white sphere. Attached to the farthest right black sphere is a red sphere, connected to two more black spheres, all in a row. Attached to the last black sphere of that row are two more white spheres. Attached to the first black sphere of that row is another red sphere. A black sphere, attached to two red spheres and a white sphere is attached to the black sphere on the top right of the six-sided ring.

    A table and diagram are shown. The table is made up of six columns and five rows. The header row reads: “Element,” “Quantity,” a blank space, “Average atomic mass (a m u),” a blank space, and “Subtotal (a m u).” The first column contains the symbols “C,” “H,” “O,” and a merged cell. The merged cell runs the length of the first five columns. The second column contains the numbers “9,” “8,” and “4” as well as the merged, cell. The third column contains the multiplication symbol in each cell except for the last, merged cell. The fourth column contains the numbers “12.01,” “1.008,” and “16.00” as well as the merged cell. The fifth column contains the symbol “=” in each cell except for the last, merged cell. The sixth column contains the values: “108.09,” “8.064,” “64.00,” and “180.15.” There is a thick black line below the number 64.00. The merged cell under the first five columns reads “Molecular mass.” To the left of the table is a diagram of a molecule. Six black spheres are located in a six-sided ring and connected by alternating double and single black bonds. Attached to each of the four black spheres is one smaller white sphere. Attached to the farthest right black sphere is a red sphere, connected to two more black spheres, all in a row. Attached to the last black sphere of that row are two more white spheres. Attached to the first black sphere of that row is another red sphere. A black sphere, attached to two red spheres and a white sphere is attached to the black sphere on the top right of the six-sided ring. Figure \(\PageIndex{2}\): The average mass of an aspirin molecule is 180.15 amu. The model shows the molecular structure of aspirin, C9H8O4.

    Example \(\PageIndex{1}\): Computing Molecular Mass for a Covalent Compound

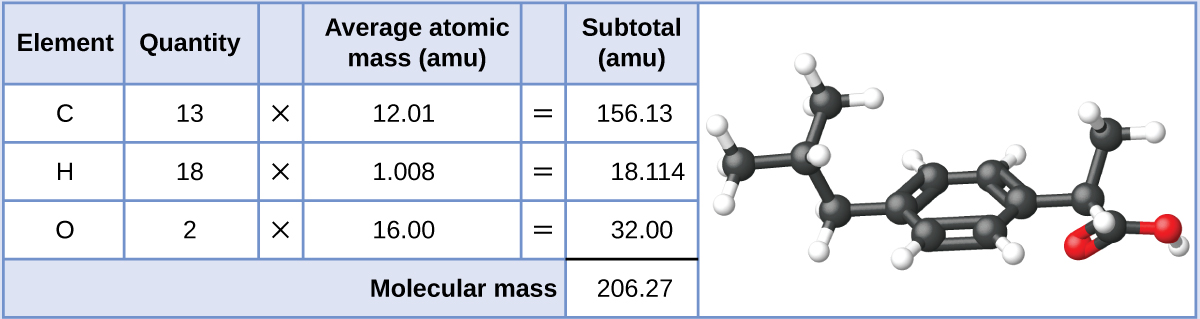
    Ibuprofen, C13H18O2, is a covalent compound and the active ingredient in several popular nonprescription pain medications, such as Advil and Motrin. What is the molecular mass (amu) for this compound?

    Solution

    Molecules of this compound are comprised of 13 carbon atoms, 18 hydrogen atoms, and 2 oxygen atoms. Following the approach described above, the average molecular mass for this compound is therefore:

    CNX_Chem_03_01_ibuprofenmass_img.jpg

    Exercise \(\PageIndex{1}\)

    Acetaminophen, C8H9NO2, is a covalent compound and the active ingredient in several popular nonprescription pain medications, such as Tylenol. What is the molecular mass (amu) for this compound?

    Answer

    151.16 amu

     

    Formula Mass for Ionic Compounds

    Ionic compounds are composed of discrete cations and anions combined in ratios to yield electrically neutral bulk matter. The formula mass for an ionic compound is calculated in the same way as the formula mass for covalent compounds: by summing the average atomic masses of all the atoms in the compound’s formula. Keep in mind, however, that the formula for an ionic compound does not represent the composition of a discrete molecule, so it may not correctly be referred to as the “molecular mass.”

    As an example, consider sodium chloride, NaCl, the chemical name for common table salt. Sodium chloride is an ionic compound composed of sodium cations, Na+, and chloride anions, Cl−, combined in a 1:1 ratio. The formula mass for this compound is computed as 58.44 amu (Figure \(\PageIndex{3}\)).

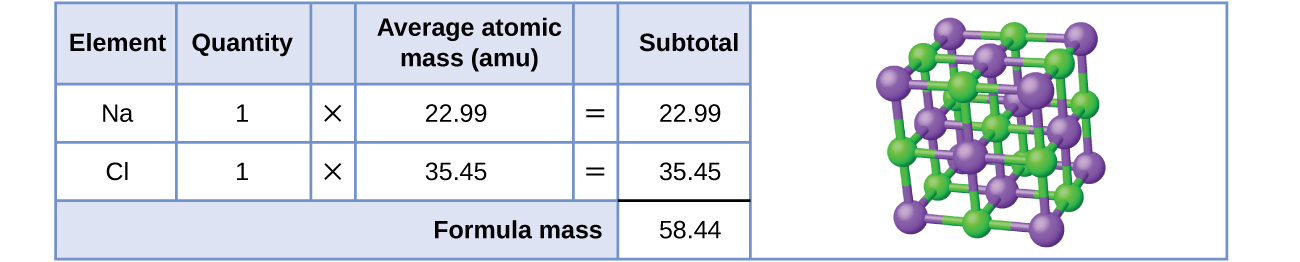
    A table and diagram are shown. The table is made up of six columns and four rows. The header row reads: “Element,” “Quantity,” a blank space, “Average atomic mass (a m u),” a blank space and “Subtotal (a m u).” The first column contains the symbols “N a”, “C l,” and a merged cell. The merged cell runs the length of the first five columns. The second column contains the numbers “1” and “1” as well as the merged cell. The third column contains the multiplication symbol in each cell except for the last, merged cell. The fourth column contains the numbers “22.99” and “35.45” as well as the merged cell. The fifth column contains the symbol “=” in each cell except for the last, merged cell. The sixth column contains the values “22.99,” “35.45,” and “58.44.” There is a thick black line below the number “35.45.” The merged cell under the first five columns reads “Formula mass.” To the left of the table is a diagram of a chemical structure. The diagram shows green and purple spheres placed in an alternating pattern, making up the corners of eight stacked cubes to form one larger cube. The green spheres are slightly smaller than the purple spheres.

    Figure \(\PageIndex{3}\): Table salt, NaCl, contains an array of sodium and chloride ions combined in a 1:1 ratio. Its formula mass is 58.44 amu.

    Note that the average masses of neutral sodium and chlorine atoms were used in this computation, rather than the masses for sodium cations and chlorine anions. This approach is perfectly acceptable when computing the formula mass of an ionic compound. Even though a sodium cation has a slightly smaller mass than a sodium atom (since it is missing an electron), this difference will be offset by the fact that a chloride anion is slightly more massive than a chloride atom (due to the extra electron). Moreover, the mass of an electron is negligibly small with respect to the mass of a typical atom. Even when calculating the mass of an isolated ion, the missing or additional electrons can generally be ignored, since their contribution to the overall mass is negligible, reflected only in the nonsignificant digits that will be lost when the computed mass is properly rounded. The few exceptions to this guideline are very light ions derived from elements with precisely known atomic masses.

    Example \(\PageIndex{2}\): Computing Formula Mass for an Ionic Compound

    Aluminum sulfate, Al2(SO4)3, is an ionic compound that is used in the manufacture of paper and in various water purification processes. What is the formula mass (amu) of this compound?

    Solution

    The formula for this compound indicates it contains Al3+ and SO42− ions combined in a 2:3 ratio. For purposes of computing a formula mass, it is helpful to rewrite the formula in the simpler format, Al2S3O12. Following the approach outlined above, the formula mass for this compound is calculated as follows:

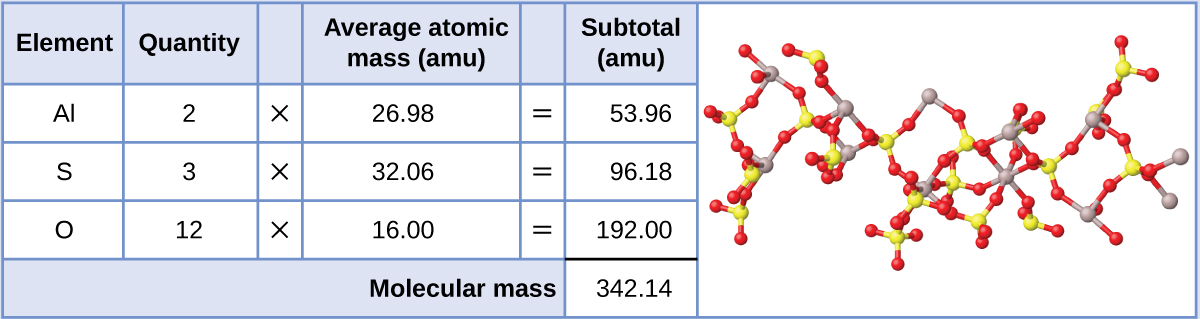
    <div data-mt-source="1"><img alt="A table is shown that is made up of six columns and five rows. The header row reads: “Element,” “Quantity,” a blank space, “Average atomic mass (a m u),” a blank space, and “Subtotal (a m u).” The first column contains the symbols “A l,” “S,” “O,” and a merged cell. The merged cell runs the length of the first five columns. The second column contains the numbers “2,” “3,” and “12” as well as the merged cell. The third column contains the multiplication symbol in each cell except for the last, merged cell. The fourth column contains the numbers “26.98,” “32.06,” and “16.00” as well as the merged cell. The fifth column contains the symbol “=” in each cell except for the last, merged cell. The sixth column contains the values “53.96,” “96.18,” “192.00,” and “342.14.” There is a thick black line under the number 192.00. The merged cell under the first five columns reads “Molecular mass.” To the right of this table is a ball-and-stick structure. It shows yellow and grey sphere connected to red spheres in a complex pattern. The yellow and grey spheres are similar in size, but the red spheres appear to be smaller by comparison." data-cke-saved-src="http://cnx.org/resources/69320dd9501e62acfadfea27070af496cb632641/CNX_Chem_03_01_alsulfatemass_img.jpg" src="http://cnx.org/resources/69320dd9501e62acfadfea27070af496cb632641/CNX_Chem_03_01_alsulfatemass_img.jpg"></div>

    Exercise \(\PageIndex{2}\)

    Calcium phosphate, Ca3(PO4)2, is an ionic compound and a common anti-caking agent added to food products. What is the formula mass (amu) of calcium phosphate?

    Answer

    310.18 amu

     

    The Mole

    In units 1 and 2, we learned about measuring quanity of atoms using the mole. As a reminder, the mole is an amount unit similar to familiar units like pair, dozen, gross, etc. The number of entities composing a mole has been experimentally determined to be \(6.02214179 \times 10^{23}\), a fundamental constant named Avogadro’s number (NA) or the Avogadro constant in honor of Italian scientist Amedeo Avogadro. This constant is properly reported with an explicit unit of “per mole,” a conveniently rounded version being \(6.022 \times 10^{23}/\ce{mol}\).

    The relationships between formula mass, the mole, and Avogadro’s number can be applied to compute various quantities that describe the composition of substances and compounds. In unit 2, we used Avogadro’s number to convert between mass of an element, moles of an element, and number of atoms in the sample. Now, we can use Avogadro’s number and formula mass (also called molecular weight) to convent between mass of a sample, moles, and number of molecules. For example, if we know the mass and chemical composition of a substance, we can determine the number of moles and calculate number of atoms or molecules in the sample. Likewise, if we know the number of moles of a substance, we can derive the number of atoms or molecules and calculate the substance’s mass.s

    Example \(\PageIndex{7}\): Deriving Moles from Grams for a Compound

    Our bodies synthesize protein from amino acids. One of these amino acids is glycine, which has the molecular formula C2H5O2N. How many moles of glycine molecules are contained in 28.35 g of glycine?

    Solution

    We can derive the number of moles of a compound from its mass following the same procedure we used for an element in Example \(\PageIndex{6}\):

    imageedit_37_6337915915.png

    The molar mass of glycine is required for this calculation, and it is computed in the same fashion as its molecular mass. One mole of glycine, C2H5O2N, contains 2 moles of carbon, 5 moles of hydrogen, 2 moles of oxygen, and 1 mole of nitrogen:

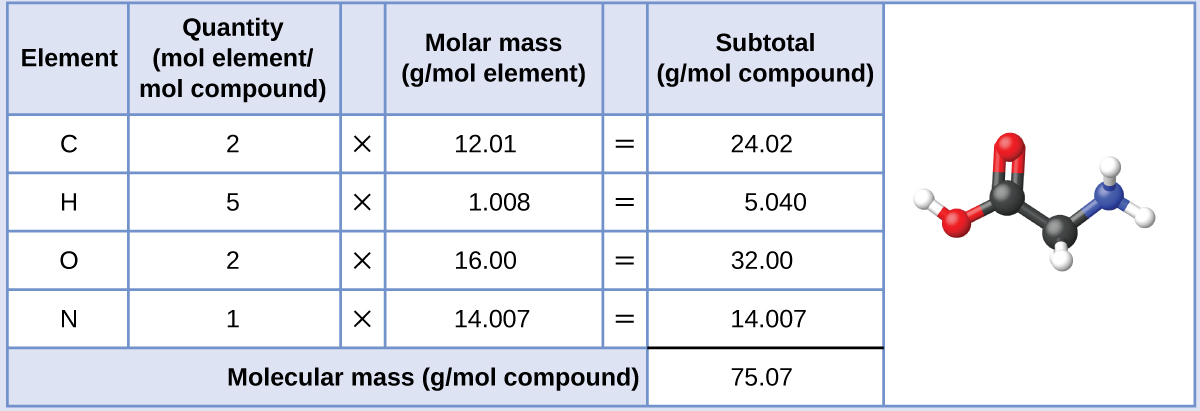
    A table is shown that is made up of six columns and six rows. The header row reads: “Element,” “Quantity (mol element / mol compound,” a blank space, “Molar mass (g / mol element),” a blank space, and “Subtotal (a m u).” The first column contains the symbols “C,” “H,” “O,” “N,” and a merged cell. The merged cell runs the width of the first five columns. The second column contains the numbers “2,” “5,” “2,” and “1” as well as the merged cell. The third column contains the multiplication symbol in each cell except for the last, merged cell. The fourth column contains the numbers “12.01,” “1.008,” “16.00,” and “14.007” as well as the merged cell. The fifth column contains the symbol “=” in each cell except for the last, merged cell. The sixth column contains the values “24.02,” “5.040,” “32.00,” “14.007,” and “75.07.” There is a thick black line under the number 14.007. The merged cell under the first five columns reads “Molar mass (g / mol compound). There is a ball-and-stick drawing to the right of this table. It shows a black sphere that forms a double bond with a slightly smaller red sphere, a single bond with another red sphere, and a single bond with another black sphere. The red sphere that forms a single bond with the black sphere also forms a single bond with a smaller, white sphere. The second black sphere forms a single bond with a smaller, white sphere and a smaller blue sphere. The blue sphere forms a single bond with two smaller, white spheres each.

    The provided mass of glycine (~28 g) is a bit more than one-third the molar mass (~75 g/mol), so we would expect the computed result to be a bit greater than one-third of a mole (~0.33 mol). Dividing the compound’s mass by its molar mass yields:

    \[\mathrm{28.35\:\cancel{g}\:glycine\left(\dfrac{mol\: glycine}{75.07\:\cancel{g}}\right)=0.378\:mol\: glycine} \nonumber\]

    This result is consistent with our rough estimate.

    Exercise \(\PageIndex{7}\)

    How many moles of sucrose, \(C_{12}H_{22}O_{11}\), are in a 25-g sample of sucrose?

    Answer

    0.073 mol

    Example \(\PageIndex{8}\): Deriving Grams from Moles for a Compound

    Vitamin C is a covalent compound with the molecular formula C6H8O6. The recommended daily dietary allowance of vitamin C for children aged 4–8 years is 1.42 × 10−4 mol. What is the mass of this allowance in grams?

    Solution

    As for elements, the mass of a compound can be derived from its molar amount as shown:

    imageedit_42_2246003702.png

    The molar mass for this compound is computed to be 176.124 g/mol. The given number of moles is a very small fraction of a mole (~10−4 or one-ten thousandth); therefore, we would expect the corresponding mass to be about one-ten thousandth of the molar mass (~0.02 g). Performing the calculation, we get:

    \[\mathrm{1.42\times10^{-4}\:\cancel{mol}\:vitamin\: C\left(\dfrac{176.124\:g}{\cancel{mol}\:vitamin\: C}\right)=0.0250\:g\: vitamin\: C} \nonumber\]

    This is consistent with the anticipated result.

    Exercise \(\PageIndex{8}\)

    What is the mass of 0.443 mol of hydrazine, \(N_2H_4\)?

    Answer

    14.2 g

    Example \(\PageIndex{9}\): Deriving the Number of Molecules from the Compound Mass

    A packet of an artificial sweetener contains 40.0 mg of saccharin (C7H5NO3S), which has the structural formula:

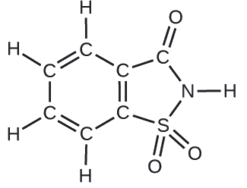
    imageedit_47_3511987581.png

    Given that saccharin has a molar mass of 183.18 g/mol, how many saccharin molecules are in a 40.0-mg (0.0400-g) sample of saccharin? How many carbon atoms are in the same sample?

    Solution

    The number of molecules in a given mass of compound is computed by first deriving the number of moles, as demonstrated in Example \(\PageIndex{8}\), and then multiplying by Avogadro’s number:

    imageedit_53_5033193793.png

    Using the provided mass and molar mass for saccharin yields:

    \[\mathrm{0.0400\:\cancel{g}\:\ce{C7H5NO3S}\left(\dfrac{\cancel{mol}\:\ce{C7H5NO3S}}{183.18\:\cancel{g}\:\ce{C7H5NO3S}}\right)\left(\dfrac{6.022\times10^{23}\:\ce{C7H5NO3S}\:molecules}{1\:\cancel{mol}\:\ce{C7H5NO3S}}\right)}\\
    =\mathrm{1.31\times10^{20}\:\ce{C7H5NO3S}\:molecules}\]

    The compound’s formula shows that each molecule contains seven carbon atoms, and so the number of C atoms in the provided sample is:

    \[\mathrm{1.31\times10^{20}\:\ce{C7H5NO3S}\: molecules\left(\dfrac{7\:C\: atoms}{1\:\ce{C7H5NO3S}\: molecule}\right)=9.20\times10^{21}\:C\: atoms} \nonumber\]

    Exercise \(\PageIndex{9}\)

    How many \(C_4H_{10}\) molecules are contained in 9.213 g of this compound? How many hydrogen atoms?

    Answer
    • \(9.545 \times 10^{22}\; \text{molecules}\; C_4H_{10}\)
    • \(9.545 \times 10^{23 }\;\text{atoms}\; H\)

    Video \(\PageIndex{3}\): A preview of some of the uses we will have for moles in upcoming units

    Percent Composition

    In the previous section, we discussed the relationship between the bulk mass of a substance and the number of atoms or molecules it contains (moles). Given the chemical formula of the substance, we were able to determine the amount of the substance (moles) from its mass, and vice versa. But what if the chemical formula of a substance is unknown? In this section, we will explore how to apply these very same principles in order to derive the chemical formulas of unknown substances from experimental mass measurements.

    The elemental makeup of a compound defines its chemical identity, and chemical formulas are the most succinct way of representing this elemental makeup. When a compound’s formula is unknown, measuring the mass of each of its constituent elements is often the first step in the process of determining the formula experimentally. The results of these measurements permit the calculation of the compound’s percent composition, defined as the percentage by mass of each element in the compound. For example, consider a gaseous compound composed solely of carbon and hydrogen. The percent composition of this compound could be represented as follows:

    \[\mathrm{\%H=\dfrac{mass\: H}{mass\: compound}\times100\%}\]

    \[\mathrm{\%C=\dfrac{mass\: C}{mass\: compound}\times100\%}\]

    If analysis of a 10.0-g sample of this gas showed it to contain 2.5 g H and 7.5 g C, the percent composition would be calculated to be 25% H and 75% C:

    \[\mathrm{\%H=\dfrac{2.5\:g\: H}{10.0\:g\: compound}\times100\%=25\%}\]

    \[\mathrm{\%C=\dfrac{7.5\:g\: C}{10.0\:g\: compound}\times100\%=75\%}\]

    Example \(\PageIndex{10}\): Calculation of Percent Composition

    Analysis of a 12.04-g sample of a liquid compound composed of carbon, hydrogen, and nitrogen showed it to contain 7.34 g C, 1.85 g H, and 2.85 g N. What is the percent composition of this compound?

    Solution

    To calculate percent composition, we divide the experimentally derived mass of each element by the overall mass of the compound, and then convert to a percentage:

    \[\mathrm{\%C=\dfrac{7.34\:g\: C}{12.04\:g\: compound}\times100\%=61.0\%} \nonumber\]

    \[\mathrm{\%H=\dfrac{1.85\:g\: H}{12.04\:g\: compound}\times100\%=15.4\%} \nonumber\]

    \[\mathrm{\%N=\dfrac{2.85\:g\: N}{12.04\:g\: compound}\times100\%=23.7\%} \nonumber\]

    The analysis results indicate that the compound is 61.0% C, 15.4% H, and 23.7% N by mass.

    Exercise \(\PageIndex{10}\)

    A 24.81-g sample of a gaseous compound containing only carbon, oxygen, and chlorine is determined to contain 3.01 g C, 4.00 g O, and 17.81 g Cl. What is this compound’s percent composition?

    Answer

    12.1% C, 16.1% O, 71.8% Cl

     

    Determining Percent Composition from Formula Mass

    Video \(\PageIndex{4}\): A video overview of how to calculate percent composition of a compound based on its chemical formula.

    Percent composition is also useful for evaluating the relative abundance of a given element in different compounds of known formulas. As one example, consider the common nitrogen-containing fertilizers ammonia (NH3), ammonium nitrate (NH4NO3), and urea (CH4N2O). The element nitrogen is the active ingredient for agricultural purposes, so the mass percentage of nitrogen in the compound is a practical and economic concern for consumers choosing among these fertilizers. For these sorts of applications, the percent composition of a compound is easily derived from its formula mass and the atomic masses of its constituent elements. A molecule of NH3 contains one N atom weighing 14.01 amu and three H atoms weighing a total of (3 × 1.008 amu) = 3.024 amu. The formula mass of ammonia is therefore (14.01 amu + 3.024 amu) = 17.03 amu, and its percent composition is:

    \[\mathrm{\%N=\dfrac{14.01\:amu\: N}{17.03\:amu\:NH_3}\times100\%=82.27\%}\]

    \[\mathrm{\%H=\dfrac{3.024\:amu\: N}{17.03\:amu\:NH_3}\times100\%=17.76\%}\]

    This same approach may be taken considering a pair of molecules, a dozen molecules, or a mole of molecules, etc. The latter amount is most convenient and would simply involve the use of molar masses instead of atomic and formula masses, as demonstrated Example \(\PageIndex{2}\). As long as we know the chemical formula of the substance in question, we can easily derive percent composition from the formula mass or molar mass.

    Example \(\PageIndex{11}\): Determining Percent Composition from a Molecular Formula

    Aspirin is a compound with the molecular formula C9H8O4. What is its percent composition?

    Solution

    To calculate the percent composition, we need to know the masses of C, H, and O in a known mass of C9H8O4. It is convenient to consider 1 mol of C9H8O4 and use its molar mass (180.159 g/mole, determined from the chemical formula) to calculate the percentages of each of its elements:

    \[\begin{align*}
    \%\ce C&=\mathrm{\dfrac{9\:mol\: C\times molar\: mass\: C}{molar\: mass\:\ce{C9H18O4}}\times100=\dfrac{9\times12.01\:g/mol} \nonumber{180.159\:g/mol}\times100=\dfrac{108.09\:g/mol}{180.159\:g/mol}\times100} \nonumber\\
    \%\ce C&=\mathrm{60.00\,\%\,C} \nonumber
    \end{align*}\]

    \[\begin{align*}
    \%\ce H&=\mathrm{\dfrac{8\:mol\: H\times molar\: mass\: H}{molar\: mass\:\ce{C9H18O4}}\times 100=\dfrac{8\times 1.008\:g/mol} \nonumber {180.159\:g/mol}\times 100=\dfrac{8.064\:g/mol}{180.159\:g/mol}\times 100} \nonumber\\
    \%\ce H&=4.476\,\%\,\ce H\nonumber
    \end{align*}\]

    \[\begin{align*}
    \%\ce O&=\mathrm{\dfrac{4\:mol\: O\times molar\: mass\: O}{molar\: mass\: \ce{C9H18O4}}\times 100=\dfrac{4\times 16.00\:g/mol} \nonumber{180.159\:g/mol}\times 100=\dfrac{64.00\:g/mol}{180.159\:g/mol}\times 100} \nonumber \\
    \%\ce O&=35.52\% \nonumber
    \end{align*}\]

    Note that these percentages sum to equal 100.00% when appropriately rounded.

    Exercise \(\PageIndex{11}\)

    To three significant digits, what is the mass percentage of iron in the compound \(Fe_2O_3\)?

    Answer

    69.9% Fe

    Summary

    The formula mass of a substance is the sum of the average atomic masses of each atom represented in the chemical formula and is expressed in atomic mass units. The formula mass of a covalent compound is also called the molecular mass. A convenient amount unit for expressing very large numbers of atoms or molecules is the mole. Experimental measurements have determined the number of entities composing 1 mole of substance to be 6.022 × 1023, a quantity called Avogadro’s number. The mass in grams of 1 mole of substance is its molar mass. Due to the use of the same reference substance in defining the atomic mass unit and the mole, the formula mass (amu) and molar mass (g/mol) for any substance are numerically equivalent (for example, one H2O molecule weighs approximately 18 amu and 1 mole of H2O molecules weighs approximately 18 g).

    Footnotes

    1. 1 Omiatek, Donna M., Amanda J. Bressler, Ann-Sofie Cans, Anne M. Andrews, Michael L. Heien, and Andrew G. Ewing. “The Real Catecholamine Content of Secretory Vesicles in the CNS Revealed by Electrochemical Cytometry.” Scientific Report 3 (2013): 1447, accessed January 14, 2015, doi:10.1038/srep01447.
    2. Read more about the redefinition of SI units including the kilogram here (Laura Howe, CE&N, Nov. 16, 2018).

    Glossary

    Avogadro’s number (NA)
    experimentally determined value of the number of entities comprising 1 mole of substance, equal to 6.022 × 1023 mol−1
    formula mass
    sum of the average masses for all atoms represented in a chemical formula; for covalent compounds, this is also the molecular mass
    mole
    amount of substance containing the same number of atoms, molecules, ions, or other entities as the number of atoms in exactly 12 grams of 12C
    molar mass
    mass in grams of 1 mole of a substance
    percent composition
    percentage by mass of the various elements in a compound

    Contributors

    • Paul Flowers (University of North Carolina - Pembroke), Klaus Theopold (University of Delaware) and Richard Langley (Stephen F. Austin State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at http://cnx.org/contents/85abf193-2bd...a7ac8df6@9.110).

    • Adelaide Clark, Oregon Institute of Technology
    • Crash Course Chemistry: Crash Course is a division of Complexly and videos are free to stream for educational purposes.
    • TED-Ed’s commitment to creating lessons worth sharing is an extension of TED’s mission of spreading great ideas. Within TED-Ed’s growing library of TED-Ed animations, you will find carefully curated educational videos, many of which represent collaborations between talented educators and animators nominated through the TED-Ed website.
    • Fuse School, Open Educational Resource free of charge, under a Creative Commons License: Attribution-NonCommercial CC BY-NC (View License Deed: https://creativecommons.org/licenses/by-nc/4.0/)

     

    4.4: Formula Mass, Percent Composition, and the Mole is shared under a not declared license and was authored, remixed, and/or curated by LibreTexts.