1.4: Volume, Thickness, and Density
- Page ID
- 189531
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Learning Objectives
- Calculate area, volume, density, and thickness and convert to various units.
Derived SI Units
We can derive many units from the seven SI base units. For example, we can use the base unit of length to define a unit of volume, and the base units of mass and length to define a unit of density.
Volume
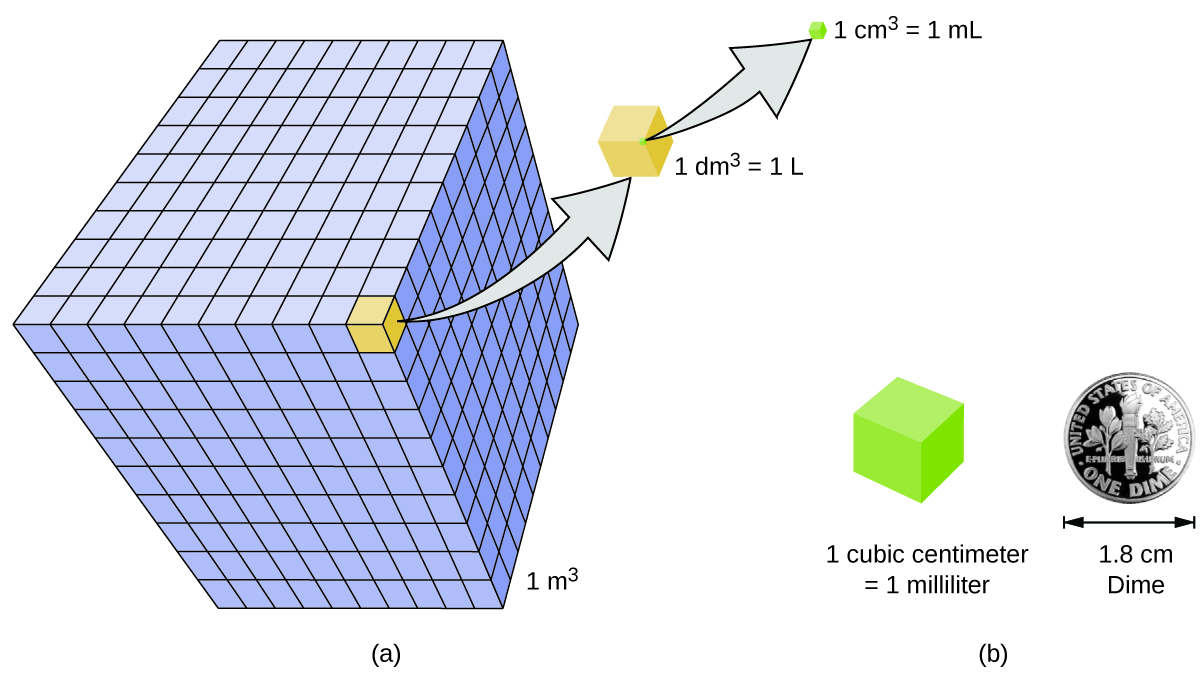
Volume is the measure of the amount of space occupied by an object. The standard SI unit of volume is defined by the base unit of length (Figure \(\PageIndex{3}\)). The standard volume is a cubic meter (m3), a cube with an edge length of exactly one meter. To dispense a cubic meter of water, we could build a cubic box with edge lengths of exactly one meter. This box would hold a cubic meter of water or any other substance.
A more commonly used unit of volume is derived from the decimeter (0.1 m, or 10 cm). A cube with edge lengths of exactly one decimeter contains a volume of one cubic decimeter (dm3). A liter (L) is the more common name for the cubic decimeter. One liter is about 1.06 quarts. A cubic centimeter (cm3) is the volume of a cube with an edge length of exactly one centimeter. The abbreviation cc (for cubic centimeter) is often used by health professionals. A cubic centimeter is also called a milliliter (mL) and is 1/1000 of a liter.
 <
<
Density
We use the mass and volume of a substance to determine its density. Thus, the units of density are defined by the base units of mass and length.
The density of a substance is the ratio of the mass of a sample of the substance to its volume. The SI unit for density is the kilogram per cubic meter (kg/m3). For many situations, however, this as an inconvenient unit, and we often use grams per cubic centimeter (g/cm3) for the densities of solids and liquids, and grams per liter (g/L) for gases. Although there are exceptions, most liquids and solids have densities that range from about 0.7 g/cm3 (the density of gasoline) to 19 g/cm3 (the density of gold). The density of air is about 1.2 g/L. Table \(\PageIndex{3}\) shows the densities of some common substances.
| Solids | Liquids | Gases (at 25 °C and 1 atm) |
|---|---|---|
| ice (at 0 °C) 0.92 g/cm3 | water 1.0 g/cm3 | dry air 1.20 g/L |
| oak (wood) 0.60–0.90 g/cm3 | ethanol 0.79 g/cm3 | oxygen 1.31 g/L |
| iron 7.9 g/cm3 | acetone 0.79 g/cm3 | nitrogen 1.14 g/L |
| copper 9.0 g/cm3 | glycerin 1.26 g/cm3 | carbon dioxide 1.80 g/L |
| lead 11.3 g/cm3 | olive oil 0.92 g/cm3 | helium 0.16 g/L |
| silver 10.5 g/cm3 | gasoline 0.70–0.77 g/cm3 | neon 0.83 g/L |
| gold 19.3 g/cm3 | mercury 13.6 g/cm3 | radon 9.1 g/L |
While there are many ways to determine the density of an object, perhaps the most straightforward method involves separately finding the mass and volume of the object, and then dividing the mass of the sample by its volume. In the following example, the mass is found directly by weighing, but the volume is found indirectly through length measurements.
\[\mathrm{density=\dfrac{mass}{volume}}\]
Example \(\PageIndex{1}\)
Calculation of Density Gold—in bricks, bars, and coins—has been a form of currency for centuries. In order to swindle people into paying for a brick of gold without actually investing in a brick of gold, people have considered filling the centers of hollow gold bricks with lead to fool buyers into thinking that the entire brick is gold. It does not work: Lead is a dense substance, but its density is not as great as that of gold, 19.3 g/cm3. What is the density of lead if a cube of lead has an edge length of 2.00 cm and a mass of 90.7 g?
Solution
The density of a substance can be calculated by dividing its mass by its volume. The volume of a cube is calculated by cubing the edge length.
\[\mathrm{volume\: of\: lead\: cube=2.00\: cm\times2.00\: cm\times2.00\: cm=8.00\: cm^3}\]
\[\mathrm{density=\dfrac{mass}{volume}=\dfrac{90.7\: g}{8.00\: cm^3}=\dfrac{11.3\: g}{1.00\: cm^3}=11.3\: g/cm^3}\]
Exercise \(\PageIndex{1}\)
- To three decimal places, what is the volume of a cube (cm3) with an edge length of 0.843 cm?
- If the cube in part (a) is copper and has a mass of 5.34 g, what is the density of copper to two decimal places?
- Answer a
-
0.599 cm3;
- Answer b
-
8.91 g/cm3
Example \(\PageIndex{2}\): Using Displacement of Water to Determine Density
This PhET simulation illustrates another way to determine density, using displacement of water. Determine the density of the red and yellow blocks.
Solution
When you open the density simulation and select Same Mass, you can choose from several 5.00-kg colored blocks that you can drop into a tank containing 100.00 L water. The yellow block floats (it is less dense than water), and the water level rises to 105.00 L. While floating, the yellow block displaces 5.00 L water, an amount equal to the weight of the block. The red block sinks (it is more dense than water, which has density = 1.00 kg/L), and the water level rises to 101.25 L.
The red block therefore displaces 1.25 L water, an amount equal to the volume of the block. The density of the red block is:
\[\mathrm{density=\dfrac{mass}{volume}=\dfrac{5.00\: kg}{1.25\: L}=4.00\: kg/L}\]
Note that since the yellow block is not completely submerged, you cannot determine its density from this information. But if you hold the yellow block on the bottom of the tank, the water level rises to 110.00 L, which means that it now displaces 10.00 L water, and its density can be found:
\[\mathrm{density=\dfrac{mass}{volume}=\dfrac{5.00\: kg}{10.00\: L}=0.500\: kg/L}\]
Exercise \(\PageIndex{1}\)
Remove all of the blocks from the water and add the green block to the tank of water, placing it approximately in the middle of the tank. Determine the density of the green block.
- Answer
-
2.00 kg/L
Thickness
The width of an object is also sometimes defined as thickness (T). This generally occurs when the width of the object is significantly smaller than the other dimensions. Measuring thickness requires a tool with great precision such as calipers. However, if you know the area, mass, and density of a substance, then you could calculate the thickness.
Use this formula to calculate thickness: \(\mathrm{thickness=\dfrac{volume}{area}}\)
To find the volume, you would rearrange the density formula. \(\mathrm{volume=\dfrac{mass}{density}}\)
Example \(\PageIndex{2}\): Calculating Thickness
A piece of aluminum foil has a mass of 0.018g and is 5.0cm on each side. Given the density of aluminum is 2.7g/cc, what is the thickness of aluminum in cm?
Solution
\(\mathrm{thickness=\dfrac{volume}{area}}\)
First find the volume of the foil.
\[\mathrm{volume=\dfrac{mass}{density}=\dfrac{0.018\: g}{2.7\: g/cc}=0.00667\: cc}\]
Next find the area of the foil.
\[\mathrm{area =5.0\: cm\times5.0\: cm=25\: cm^2}\]
Solve for Thickness
\[\mathrm{thickness=\dfrac{volume}{area}=\dfrac{0.00667\: cc}{25\: cm^2}=0.00027\: cm}\]
Summary
Scientists use derived units, such as liters (for volume) and g/cm3 (for density). Thickness is a way to express the width of an object when that dimension is small.
Key Equations
- \(\mathrm{density=\dfrac{mass}{volume}}\)
- \(\mathrm{thickness=\dfrac{volume}{area}}\)
Glossary
- density
- ratio of mass to volume for a substance or object
- liter (L)
- (also, cubic decimeter) unit of volume; 1 L = 1,000 cm3
- milliliter (mL)
- 1/1,000 of a liter; equal to 1 cm3
- second (s)
- SI unit of time
- SI units (International System of Units)
- standards fixed by international agreement in the International System of Units (Le Système International d’Unités)
- thickness
- another way to express the width of an object which can be caluculated by taking the volume of the object divided by the area
- volume
- amount of space occupied by an object
Contributors
Paul Flowers (University of North Carolina - Pembroke), Klaus Theopold (University of Delaware) and Richard Langley (Stephen F. Austin State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at http://cnx.org/contents/85abf193-2bd...a7ac8df6@9.110).
- Christy VanRooyen, Oregon Tech


