13.3: Radiochemistry

Atoms having the same number of protons but a different number of neutrons are isotopes. To identify an isotope we use the notation \(_Z^AE\), where E is the element’s atomic symbol, Z is the element’s atomic number, and A is the element’s atomic mass number. Although an element’s different isotopes have the same chemical properties, their nuclear properties are different. The most important difference between isotopes is their stability. The nuclear configuration of a stable isotope remains constant with time. Unstable isotopes, however, spontaneously disintegrate, emitting radioactive particles as they transform into a more stable form.

An element’s atomic number is equal to the number of protons and its atomic mass is equal to the sum of the number of protons and neutrons. We represent an isotope of carbon-13 as

\(\ce{_6^{13}C}\)

because carbon has 6 protons and 7 neutrons. Sometimes we omit Z from this notation—identifying the element and the atomic number is repetitive because all isotopes of carbon have 6 protons and any atom having 6 protons is an isotope of carbon. Thus, ¹³C and C–13 are alternative notations for this isotope of carbon.

The most important types of radioactive particles are alpha particles, beta particles, gamma rays, and X-rays. An alpha particle, α, is equivalent to a helium nucleus, \(\ce{_2^4He}\). When an atom emits an alpha particle, the product in a new atom whose atomic number and atomic mass number are, respectively, 2 and 4 less than its unstable parent. The decay of uranium to thorium is one example of alpha emission.

\[\ce{_{92}^{238}U → _{90}^{234}Th + α}\]

A beta particle, β, comes in one of two forms. A negatron, \(\ce{_{-1}^0β}\), is produced when a neutron changes into a proton, increasing the atomic number by one, as shown here for lead.

\[\ce{_{82}^{214}Pb → _{83}^{214}Bi + _{−1}^0β}\]

Negatrons

A negatron, which is the more common type of beta particle, is equivalent to an electron. You may recall from Section 12.4.5 that the electron capture detector for gas chromatography uses ⁶³Ni as a beta emitter.

The conversion of a proton to a neutron results in the emission of a positron, \(_1^0β\).

\[\ce{_{15}^{30}P → _{14}^{30}Si + _1^0β}\]

The emission of an alpha or a beta particle often produces an isotope in an unstable, high energy state. This excess energy is released as a gamma ray, γ, or as an X-ray. Gamma ray and X-ray emission may also occur without the release of an alpha particle or a beta particle.

13.3.1 Theory and Practice

A radioactive isotope’s rate of decay, or activity, follows first-order kinetics

\[A = -\dfrac{dN}{dt} = λN\label{13.34}\]

where A is the activity, N is the number of radioactive atoms present in the sample at time t, and λ is the isotope’s decay constant. Activity is expressed as the number of disintegrations per unit time.

Note the similarity between Equation \(\ref{13.34}\) and Equation 13.1

\[\textrm{rate} = -\dfrac{d[\ce A]}{dt} =k[\ce A] \nonumber\]

where activity is equivalent to rate, N is equivalent to [A], and l is equivalent to k.

As with any first-order process, we can rewrite Equation \(\ref{13.24}\) in an integrated form.

\[N_\ce{t} = N_0e^{−λt}\label{13.35}\]

Substituting Equation \(\ref{13.35}\) into Equation \(\ref{13.34}\) gives

\[A = λN_0e^{-λt}=A_0e^{-λt}\label{13.36}\]

If we measure a sample’s activity at time t we can determine the sample’s initial activity, A₀, or the number of radioactive atoms originally present in the sample, N₀.

An important characteristic property of a radioactive isotope is its half-life, t_1/2, which is the amount of time required for half of the radioactive atoms to disintegrate. For first-order kinetics the half-life is

\[t_{1/2} = \dfrac{0.693}{λ}\label{13.37}\]

Because the half-life is independent of the number of radioactive atoms, it remains constant throughout the decay process. For example, if 50% of the radioactive atoms remain after one half-life, then 25% remain after two half-lives, and 12.5% remain after three half-lives.

Suppose we begin with an N₀ of 1200 atoms During the first half-life, 600 atoms disintegrate and 600 remain. During the second half-life, 300 of the 600 remaining atoms disintegrate, leaving 300 atoms or 25% of the original 1200 atoms. Of the 300 remaining atoms, only 150 remain after the third half-life, or 12.5% of the original 1200 atoms.

Kinetic information about a radioactive isotope is usually given in terms of its half-life because it provides a more intuitive sense of the isotope’s stability. Knowing, for example, that the decay constant for \(\ce{_{38}^{90}Sr}\) is 0.0247 yr^–1 does not give an immediate sense of how fast it disintegrates. On the other hand, knowing that its half-life is 28.1 y makes it clear that the concentration of \(\ce{_{38}^{90}Sr}\) in a sample remains essentially constant over a short period of time.

13.3.2 Instrumentation

Alpha particles, beta particles, gamma rays, and X-rays are measured by using the particle’s energy to produce an amplified pulse of electrical current in a detector. These pulses are counted to give the rate of disintegration. Three types of detectors commonly are encountered: gas-filled detectors, scintillation counters, and semiconductor detectors. A gas-filled detector consists of a tube containing an inert gas, such as Ar. When a radioactive particle enters the tube it ionizes the inert gas, producing an Ar⁺/e^– ion-pair. Movement of the electron toward the anode and the Ar⁺ toward the cathode generates a measurable electrical current. A Geiger counter is one example of a gas-filled detector. A scintillation counter uses a fluorescent material to convert radioactive particles into easily measurable photons. For example, a solid-state scintillation counter consisting of a NaI crystal containing 0.2% TlI produces several thousand photons for each radioactive particle. Finally, in a semiconductor detector, adsorption of a single radioactive particle promotes thousands of electrons to the semiconductor’s conduction band, increasing conductivity.

You can learn more about these radiation detectors and the signal processors used to count particles by consulting this chapter’s additional resources.

13.3.3 Quantitative Applications

In this section we consider three common quantitative radiochemical methods of analysis: the direct analysis of a radioactive isotope by measuring its rate of disintegration, neutron activation, and isotope dilution.

Direct Analysis of Radioactive Analytes

The concentration of a long-lived radioactive isotope remains essentially constant during the period of analysis. As shown in Example 13.9, we can use the sample’s activity to calculate the number of radioactive particles in the sample.

Example 13.9

The activity in a 10.00-mL sample of wastewater containing \(\ce{_{38}^{90}Sr}\) is 9.07 × 10⁶ disintegrations/s. What is the molar concentration of \(\ce{_{38}^{90}Sr}\) in the sample? The half-life for \(\ce{_{38}^{90}Sr}\) is 28.1 yr.

Solution

Solving equation 13.37 for λ, substituting into Equation \(\ref{13.34}\), and solving for N gives

\[N = \dfrac{A × t_{1/2}}{0.693}\]

Before we can determine the number of atoms of \(\ce{_{38}^{90}Sr}\) in the sample we must express its activity and its half-life using the same units. Converting the half-life to seconds gives t_1/2 as 8.86 × 10⁸ s; thus, there are

\[\mathrm{\dfrac{(9.07×10^6\: disintergrations/s)(8.86×10^8\: s)}{0.693} = 1.16×10^{16}\: atoms\: _{38}^{90}Sr}\]

The concentration of \(\ce{_{38}^{90}Sr}\) in the sample is

\[\mathrm{\dfrac{1.16×10^{16}\: atoms\: _{38}^{90}Sr}{(6.022×10^{23}\: atom/mol)(0.01000\: L)} = 1.93×10^{-6}\: M\: _{38}^{90}Sr}\]

The direct analysis of a short-lived radioactive isotope using the method outlined in Example 13.9 is less useful because it provides only a transient measure of the isotope’s concentration. Instead, we can measure its activity after an elapsed time, t, and use Equation \(\ref{13.36}\) to calculate N₀.

Neutron Activation Analysis

Few analytes are naturally radioactive. For many analytes, however, we can induce radioactivity by irradiating the sample with neutrons in a process called neutron activation analysis (NAA). The radioactive element formed by neutron activation decays to a stable isotope by emitting a gamma ray, and, possibly, other nuclear particles. The rate of gamma-ray emission is proportional to the analyte’s initial concentration in the sample. For example, if we place a sample containing non-radioactive \(\ce{_{13}^{27}Al}\) in a nuclear reactor and irradiate it with neutrons, the following nuclear reaction takes place.

\[\ce{_13^{27}Al + _0^1n → _{13}^{28}Al}\]

The radioactive isotope of \(\ce{_{13}^{28}Al}\) has a characteristic decay process that includes the release of a beta particle and a gamma ray.

\[\ce{_{13}^{28}Al → _{14}^{28}Si + _{−1}^0β + γ}\]

When irradiation is complete, we remove the sample from the nuclear reactor, allow any short-lived radioactive interferences to decay into the background, and measure the rate of gamma-ray emission.

The initial activity at the end of irradiation depends on the number of atoms that are present. This, in turn, is a equal to the difference between the rate of formation for \(\ce{_{13}^{28}Al}\) and its rate of disintegration

\[\dfrac{dN_\ce{_{13}^{28}Al}}{dt} = ΦσN_\ce{_{13}^{27}Al} - λN_\ce{_{13}^{28}Al}\label{13.38}\]

where Φ is the neutron flux and σ is the reaction cross-section, or probability that a \(\ce{_{13}^{27}Al}\) nucleus captures a neutron. Integrating equation 13.38 over the time of irradiation, t_i, and multiplying by λ gives the initial activity, A₀, at the end of irradiation as

\[A_0 = λN_\ce{_{13}^{28}Al} = ΦσN_\ce{_{13}^{28}Al}(1-e^{-λt_\ce{i}})\]

If we know the values for A₀, Φ, σ, λ, and t_i, then we can calculate the number of atoms of \(\ce{_{13}^{27}Al}\) initially present in the sample.

A simpler approach is to use one or more external standards. Letting (A₀)_x and (A₀)_s represent the initial activity for the analyte in an unknown and in an external standard, and letting w_x and w_s represent the analyte’s weight in the unknown and in the external standard, we obtain the following pair of equations

\[\mathrm{(A_0)_x} = kw_\ce{x}\label{13.39}\]

\[\mathrm{(A_0)_s} = kw_\ce{s}\label{13.40}\]

that we can solve to determine the analyte’s mass in the sample.

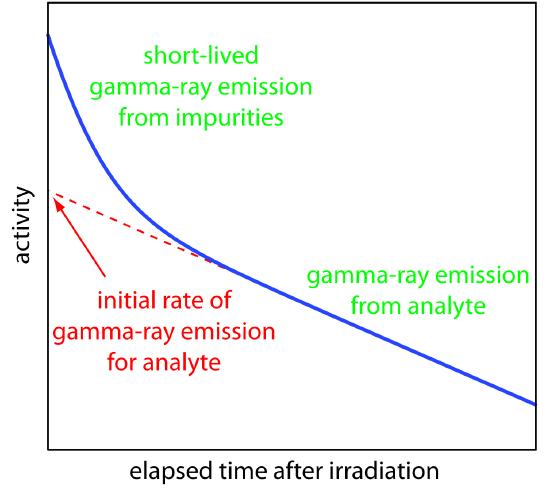
As noted earlier, gamma ray emission is measured following a period during which we allow short-lived interferents to decay into the background. As shown in Figure 13.17, we determine the sample’s and the standard’s initial activity by extrapolating a curve of activity versus time back to t = 0. Alternatively, if we irradiate the sample and the standard simultaneously, and if we measure their activities at the same time, then we can substitute these activities for (A₀)_x and (A₀)_s. This is the strategy used in the following example.

Figure 13.17 Plot of gamma-ray emission as a function of time showing how the analyte’s initial activity is determined.

Example 13.10

The concentration of Mn in steel can be determined by a neutron activation analysis using the method of external standards. A 1.000-g sample of an unknown steel sample and a 0.950-g sample of a standard steel known to contain 0.463% w/w Mn are irradiated with neutrons in a nuclear reactor for 10 h. After a 40-min delay the gamma ray emission is 2542 cpm (counts per minute) for the unknown and 1984 cpm for the external standard. What is the %w/w Mn in the unknown steel sample?

Solution

Combining equation 13.39 and equation 13.40 gives

\[w_x= \dfrac{A_x}{A_s}× w_s\]

The weight of Mn in the external standard is

\[w_\ce{s} = \mathrm{\dfrac{0.00463\: g\: Mn}{g\: steel} × 0.950\: g\: steel = 0.00440\: g\: Mn}\]

Substituting into the above equation gives

\[w_\ce{x}= \mathrm{\dfrac{2542\: cpm}{1984\: cpm} × 0.00440\: g\: Mn = 0.00564\: g\: Mn}\]

Because the original mass of steel is 1.000 g, the %w/w Mn is 0.564%.

Among the advantages of neutron activation are its applicability to almost all elements in the periodic table and that it is nondestructive to the sample. Consequently, NAA is an important technique for analyzing archeological and forensic samples, as well as works of art.

Isotope Dilution

Another important radiochemical method for the analysis of nonradioactive analytes is isotope dilution. An external source of analyte is prepared in a radioactive form with a known activity, A_T, for its radioactive decay—we call this form of the analyte a tracer. To prepare a sample for analysis we add a known mass of the tracer, w_T, to a portion of sample containing an unknown mass, w_x, of analyte. After homogenizing the sample and tracer, we isolate w_A grams of analyte by using a series of appropriate chemical and physical treatments. Because our processing techniques cannot distinguish between radioactive and nonradioactive forms of the analyte, the isolated material contains both. Finally, we measure the activity of the isolated sample, A_A. If we recover all the analyte—both the radioactive tracer and the nonradioactive analyte—then A_A and A_T are equal and w_x = w_A – w_T. Normally, we fail to recover all the analyte. In this case A_A is less than A_T, and

\[A_\ce{A} = A_\ce{T} × \dfrac{w_\ce{A}}{w_\ce{x} + w_\ce{T}}\label{13.41}\]

The ratio of weights in Equation \(\ref{13.41}\) accounts for the loss of the activity resulting from our failure to recover all the analyte. Solving equation 13.41 for w_x gives

\[w_\ce{x} = \dfrac{A_\ce{T}}{A_\ce{A}}w_\ce{A} - w_\ce{T}\label{13.42}\]

How we process the sample depends on the analyte and the sample’s matrix. We might, for example, digest the sample to bring the analyte into solution. After filtering the sample to remove the residual solids, we might precipitate the analyte, isolate it by filtration, dry it in an oven, and obtain its weight.

Given that the goal of an analysis is to determine the amount of nonradioactive analyte in our sample, the thought that we might not recover all the analyte might strike you as unsettling. Recall from Chapter 7.7, that a single liquid–liquid extraction rarely has an extraction efficiency of 100%. One advantage of isotope dilution is that the extraction efficiency for the nonradioactive analyte and the tracer are the same. If we recover 50% of the tracer, then we also recover 50% of the nonradioactive analyte. Because we know how much tracer we added to the sample, we can determine how much of the nonradioactive analyte is in the sample.

Example 13.11

The concentration of insulin in a production vat is determined by isotope dilution. A 1.00-mg sample of insulin labeled with ¹⁴C having an activity of 549 cpm is added to a 10.0-mL sample taken from the production vat. After homogenizing the sample, a portion of the insulin is separated and purified, yielding 18.3 mg of pure insulin. The activity for the isolated insulin is measured at 148 cpm. How many mg of insulin are in the original sample?

Solution

Substituting known values into Equation \(\ref{13.42}\) gives

\[w_\ce{x}= \mathrm{\dfrac{549\: cpm}{148\: cpm} × 18.3\: mg - 1.00\: mg = 66.9\: mg\: insulin}\]

Equation \(\ref{13.41}\) and Equation \(\ref{13.42}\) are valid only if the tracer’s half-life is considerably longer than the time it takes to conduct the analysis. If this is not the case, then the decrease in activity is due both to the incomplete recovery and the natural decrease in the tracer’s activity. Table 13.1 provides a list of several common tracers for isotope dilution.

Table 13.1: Common Tracers for Isotope Dilution

isotope	half-life
^3H	12.5 years
^14C	5730 years
^32P	14.3 days
^35S	87.1 days
^45Ca	152 days
^55Fe	2.91 years
^60Co	5.3 years
^131I	8 days

An important feature of isotope dilution is that it is not necessary to recover all the analyte to determine the amount of analyte present in the original sample. Isotope dilution, therefore, is useful for the analysis of samples with complex matrices, where a complete recovery of the analyte is difficult.

13.3.4 Characterization Applications

One example of a characterization application is the determination of a sample’s age based on the decay of a radioactive isotope naturally present in the sample. The most common example is carbon-14 dating, which is used to determine the age of natural organic materials.

As cosmic rays pass through the upper atmosphere, some of the \(\ce{_7^{14}N}\) atoms in the atmosphere capture high energy neutrons, converting into \(\ce{_6^{14}C}\). The \(\ce{_6^{14}C}\) then migrates into the lower atmosphere where it oxidizes to form C-14 labeled CO₂. Animals and plants subsequently incorporate this labeled CO₂ into their tissues. Because this is a steady-state process, all plants and animals have the same ratio of \(\ce{_6^{14}C}\) to \(\ce{_6^{12}C}\) in their tissues. When an organism dies, the radioactive decay of \(\ce{_6^{14}C}\) to \(\ce{_7^{14}N}\) by \(\ce{_{-1}^0β}\) emission (t_1/2 = 5730 years) leads to predictable reduction in the \(\ce{_6^{14}C}\) to \(\ce{_6^{12}C}\) ratio. We can use the change in this ratio to date samples that are as much as 30 000 years old, although the precision of the analysis is best when the sample’s age is less than 7000 years. The accuracy of carbon-14 dating depends upon our assumption that the \(\ce{_6^{14}C}\) to \(\ce{_6^{12}C}\) ratio is constant over time. Some variation in the ratio has occurred as the result of the increased consumption of fossil fuels and the production of \(\ce{_6^{14}C}\) during the testing of nuclear weapons. A calibration curve prepared using samples of known age—these include tree rings, deep ocean sediments, coral samples, and cave deposits—limits this source of uncertainty.

There is no need to prepare a calibration curve for each analysis. Instead, there is a universal calibration curve known as IntCal. The most recent such curve, IntCal04 is described in the following paper: Reimer, P. J., et. al. “IntCal04 Terrestrial Radiocarbon Age Calibration, 0–26 Cal Kyr BP,” Radiocarbon 2004, 46, 1029–1058. This calibration spans 26 000 years (Cal Kyr) before the present (BP).

Example 13.12

To determine the age of a fabric sample the relative ratio of \(\ce{_6^{14}C}\) to \(\ce{_6^{12}C}\) was measured yielding a result of 80.9% of that found in modern fibers. How old is the fabric?

Solution

Equations 13.36 and 13.37 provide us with a method for converting a change in the ratio of \(\ce{_6^{14}C}\) to \(\ce{_6^{12}C}\) to the fabric’s age. Letting A₀ be the ratio of \(\ce{_6^{14}C}\) to \(\ce{_6^{12}C}\) in modern fibers, we assign it a value of 1.00. The ratio of \(\ce{_6^{14}C}\) to \(\ce{_6^{12}C}\) in the sample, A, is 0.809. Solving gives

\[t = \ln\dfrac{A_0}{A} × \dfrac{t_{1/2}}{0.693} = \mathrm{\ln\dfrac{1.00}{0.809} × \dfrac{5730\: yr}{0.693} = 1750\: yr}\]

Other isotopes can be used to determine a sample’s age. The age of rocks, for example, has been determined from the ratio of the number of radioactive \(\ce{_{92}^{238}U}\) atoms to the number of stable \(\ce{_{82}^{206}Pb}\) atoms produced by radioactive decay. For rocks that do not contain uranium, dating is accomplished by comparing the ratio of radioactive \(\ce{_{19}^{40}K}\) to the stable \(\ce{_{18}^{40}Ar}\). Another example is the dating of sediments collected from lakes by measuring the amount of \(\ce{_{82}^{210}Pb}\) that is present.

13.3.5 Evaluation

Radiochemical methods are routinely used for the analysis of trace analytes in macro and meso samples. The accuracy and precision of radiochemical methods are generally within the range of 1.5%. We can improve the precision.which is limited by the random nature of radioactive decay.by counting the emission of radioactive particles for as long a time as is practical. If the number of counts, M, is reasonably large (M . 100), and the counting period is significantly less than the isotope's half-life, then the percent relative standard deviation for the activity, (σ_A)_rel, is approximately

\[(σ_A)_\ce{rel} = \dfrac{1}{\sqrt{M}} × 100\]

See Figure 3.5 to review the meaning of macro and meso samples.

For example, if we determine the activity by counting 10 000 radioactive particles, then the relative standard deviation is 1%. A radiochemical method’s sensitivity is inversely proportional to (σ_A)_rel, which means we can improve the sensitivity by counting more particles. Selectivity rarely is of concern when using a radiochemical method because most samples have only a single radioactive isotope. When several radioactive isotopes are present, we can determine each isotope’s activity by taking advantage of differences in the energies of their respective radioactive particles or differences in their respective decay rates. In comparison to most other analytical techniques, radiochemical methods are usually more expensive and require more time to complete an analysis. Radiochemical methods also are subject to significant safety concerns due to the analyst’s potential exposure to high energy radiation and the need to safely dispose of radioactive waste.

Contributors

• David Harvey (DePauw University)