11.1: Overview of Electrochemistry

The focus of this chapter is on analytical techniques that use a measurement of potential, charge, or current to determine an analyte’s concentration or to characterize an analyte’s chemical reactivity. Collectively we call this area of analytical chemistry electrochemistry because its originated from the study of the movement of electrons in an oxidation–reduction reaction.

Despite the difference in instrumentation, all electrochemical techniques share several common features. Before we consider individual examples in greater detail, let’s take a moment to consider some of these similarities. As you work through the chapter, this overview will help you focus on similarities between different electrochemical methods of analysis. You will find it easier to understand a new analytical method when you can see its relationship to other similar methods.

11.1.1 Five Important Concepts

To understand electrochemistry we need to appreciate five important and interrelated concepts:

1. the electrode’s potential determines the analyte’s form at the electrode’s surface;
2. the concentration of analyte at the electrode’s surface may not be the same as its concentration in bulk solution;
3. in addition to an oxidation–reduction reaction, the analyte may participate in other reactions;
4. current is a measure of the rate of the analyte’s oxidation or reduction; and
5. we cannot simultaneously control current and potential.

The Electrode’s Potential Determines the Analyte’s Form

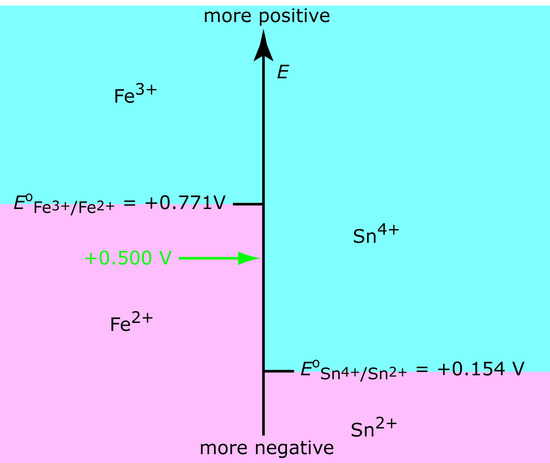
In Chapter 6 we introduced the ladder diagram as a tool for predicting how a change in solution conditions affects the position of an equilibrium reaction. For an oxidation–reduction reaction, the potential determines the reaction’s position. Figure 11.1, for example, shows a ladder diagram for the Fe³⁺/Fe²⁺ and the Sn⁴⁺/Sn²⁺ equilibria. If we place an electrode in a solution of Fe³⁺ and Sn⁴⁺ and adjust its potential to +0.500 V, Fe³⁺ reduces to Fe²⁺, but Sn⁴⁺ remains unchanged.

Note

You may wish to review the earlier treatment of oxidation–reduction reactions in Section 6.4.4 and the development of ladder diagrams for oxidation–reduction reactions in Section 6.6.3.

Figure 11.1 Redox ladder diagram for Fe³⁺/Fe²⁺ and for Sn⁴⁺/ Sn²⁺ redox couples. The areas in blue show the potential range where the oxidized forms are the predominate species; the reduced forms are the predominate species in the areas shown in pink. Note that a more positive potential favors the oxidized forms. At a potential of +0.500 V (green arrow) Fe³⁺ reduces to Fe²⁺, but Sn⁴⁺ remains unchanged.

Interfacial Concentrations May Not Equal Bulk Concentrations

In Chapter 6 we introduced the Nernst equation, which provides a mathematical relationship between the electrode’s potential and the concentrations of an analyte’s oxidized and reduced forms in solution. For example, the Nernst equation for Fe³⁺ and Fe²⁺ is

\[E = E^o − \dfrac{RT}{nF}\log\dfrac{[\ce{Fe^2+}]}{[\ce{Fe^3+}]} =E^o − \dfrac{0.05916}{1}\log\dfrac{[\ce{Fe^2+}]}{[\ce{Fe^3+}]}\tag{11.1}\]

where E is the electrode’s potential and E^o is the standard-state reduction potential for the reaction Fe³⁺ ⇋ Fe²⁺ + e⁻. Because it is the potential of the electrode that determines the analyte’s form at the electrode’s surface, the concentration terms in equation 11.1 are those at the electrode's surface, not the concentrations in bulk solution.

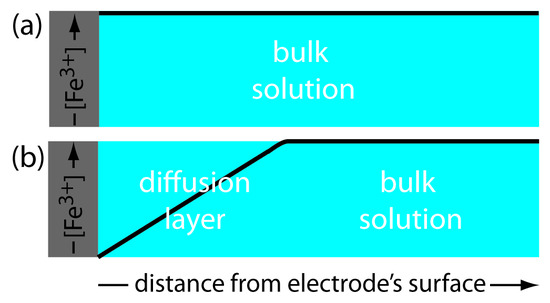
This distinction between surface concentrations and bulk concentrations is important. Suppose we place an electrode in a solution of Fe³⁺ and fix its potential at 1.00 V. From the ladder diagram in Figure 11.1, we know that Fe³⁺ is stable at this potential and, as shown in Figure 11.2a, the concentration of Fe³⁺ remains the same at all distances from the electrode’s surface. If we change the electrode’s potential to +0.500 V, the concentration of Fe³⁺ at the electrode’s surface decreases to approximately zero. As shown in Figure 11.2b, the concentration of Fe³⁺ increases as we move away from the electrode’s surface until it equals the concentration of Fe³⁺ in bulk solution. The resulting concentration gradient causes additional Fe³⁺ from the bulk solution to diffuse to the electrode’s surface.

Note

We call the solution containing this concentration gradient in Fe³⁺ the diffusion layer. We will have more to say about this in Section 11.4.2.

Figure 11.2 Concentration of Fe³⁺ as a function of distance from the electrode’s surface at (a) E = +1.00 V and (b) E = +0.500 V. The electrode is shown in gray and the solution in blue.

The Analyte May Participate in Other Reactions

Figure 11.2 shows how the electrode’s potential affects the concentration of Fe³⁺, and how the concentration of Fe³⁺ varies as a function of distance from the electrode’s surface. The reduction of Fe³⁺ to Fe²⁺, which is governed by equation 11.1, may not be the only reaction affecting the concentration of Fe³⁺ in bulk solution or at the electrode’s surface. The adsorption of Fe³⁺ at the electrode’s surface or the formation of a metal–ligand complex in bulk solution, such as Fe(OH)²⁺, also affects the concentration of Fe³⁺.

Current is a Measure of Rate

The reduction of Fe³⁺ to Fe²⁺ consumes an electron, which is drawn from the electrode. The oxidation of another species, perhaps the solvent, at a second electrode serves as the source of this electron. The flow of electrons between the electrodes provides a measurable current. Because the reduction of Fe³⁺ to Fe²⁺ consumes one electron, the flow of electrons between the electrodes—in other words, the current—is a measure of the rate of the reduction reaction. One important consequence of this observation is that the current is zero when the reaction Fe³⁺ ⇋ Fe²⁺ + e⁻ is at equilibrium.

Note

The rate of the reaction

\[\ce{Fe^3+} ⇋ \ce{Fe^2+} + e^−\]

is the change in the concentration of Fe³⁺ as a function of time.

We Cannot Simultaneously Control Both Current and Potential

If a solution of Fe³⁺ and Fe²⁺ is at equilibrium, the current is zero and the potential is given by equation 11.1. If we change the potential away from its equilibrium position, current flows as the system moves toward its new equilibrium position. Although the initial current is quite large, it decreases over time reaching zero when the reaction reaches equilibrium. The current, therefore, changes in response to the applied potential. Alternatively, we can pass a fixed current through the electrochemical cell, forcing the reduction of Fe³⁺ to Fe²⁺. Because the concentrations of Fe³⁺ and Fe²⁺ are constantly changing, the potential, as given by equation 11.1, also changes over time. In short, if we choose to control the potential, then we must accept the resulting current, and we must accept the resulting potential if we choose to control the current.

11.1.2 Controlling and Measuring Current and Potential

Electrochemical measurements are made in an electrochemical cell consisting of two or more electrodes and the electronic circuitry for controlling and measuring the current and the potential. In this section we introduce the basic components of electrochemical instrumentation.

The simplest electrochemical cell uses two electrodes. The potential of one electrode is sensitive to the analyte’s concentration, and is called the working electrode or the indicator electrode. The second electrode, which we call the counter electrode, completes the electrical circuit and provides a reference potential against which we measure the working electrode’s potential. Ideally the counter electrode’s potential remains constant so that we can assign to the working electrode any change in the overall cell potential. If the counter electrode’s potential is not constant, we replace it with two electrodes: a reference electrode whose potential remains constant and an auxiliary electrode that completes the electrical circuit.

Because we cannot simultaneously control the current and the potential, there are only three basic experimental designs: (1) we can measure the potential when the current is zero, (2) we can measure the potential while controlling the current, and (3) we can measure the current while controlling the potential. Each of these experimental designs relies on Ohm’s law, which states that a current, i, passing through an electrical circuit of resistance, R, generates a potential, E.

\[E = iR\]

Each of these experimental designs uses a different type of instrument. To help us understand how we can control and measure current and potential, we will describe these instruments as if the analyst is operating them manually. To do so the analyst observes a change in the current or the potential and manually adjusts the instrument’s settings to maintain the desired experimental conditions. It is important to understand that modern electrochemical instruments provide an automated, electronic means for controlling and measuring current and potential, and that they do so by using very different electronic circuitry.

Note

For further information about electrochemical instrumentation, see this chapter’s additional resources.

Potentiometers

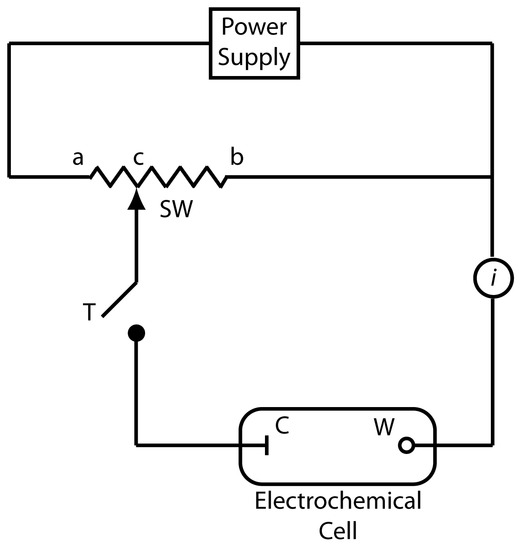
To measure the potential of an electrochemical cell under a condition of zero current we use a potentiometer. Figure 11.3 shows a schematic diagram for a manual potentiometer, consisting of a power supply, an electrochemical cell with a working electrode and a counter electrode, an ammeter for measuring the current passing through the electrochemical cell, an adjustable, slide-wire resistor, and a tap key for closing the circuit through the electrochemical cell. Using Ohm’s law, the current in the upper half of the circuit is

\[i_\ce{up} = \dfrac{E_\ce{PS}}{R_{ab}}\]

where E_PS is the power supply’s potential, and R_ab is the resistance between points a and b of the slide-wire resistor. In a similar manner, the current in the lower half of the circuit is

\[i_\ce{low} = \dfrac{E_\ce{cell}}{R_{cb}}\]

where E_cell is the potential difference between the working electrode and the counter electrode, and R_cb is the resistance between the points c and b of the slide-wire resistor. When i_up = i_low = 0, no current flows through the ammeter and the potential of the electrochemical cell is

\[E_\ce{cell}= \dfrac{R_{cb}}{R_{ab}} × E_\ce{PS}\tag{11.2}\]

To determine E_cell we momentarily press the tap key and observe the current at the ammeter. If the current is not zero, we adjust the slide wire resistor and remeasure the current, continuing this process until the current is zero. When the current is zero, we use equation 11.2 to calculate E_cell.

Using the tap key to momentarily close the circuit containing the electrochemical cell, minimizes the current passing through the cell and limits the change in the composition of the electrochemical cell. For example, passing a current of 10^–9 A through the electrochemical cell for 1 s changes the concentrations of species in the cell by approximately 10^–14 moles. Modern potentiometers use operational amplifiers to create a high-impedance voltmeter capable of measuring the potential while drawing a current of less than 10^–9 A.

Figure 11.3 Schematic diagram of a manual potentiometer: C is the counter electrode; W is the working electrode; SW is a slide-wire resistor; T is a tap key and i is an ammeter for measuring current.

Galvanostats

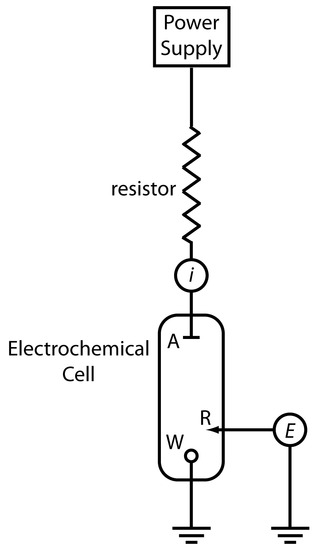
A galvanostat allows us to control the current flowing through an electrochemical cell. A schematic diagram of a constant-current galvanostat is shown in Figure 11.4. The current flowing from the power supply through the working electrode is

\[i = \dfrac{E_\ce{PS}}{R + R_\ce{cell}}\]

where E_PS is the potential of the power supply, R is the resistance of the resistor, and R_cell is the resistance of the electrochemical cell. If R >> R_cell, then the current between the auxiliary and working electrodes is

\[i = \dfrac{E_\ce{PS}}{R} ≈ \ce{constant}\]

To monitor the potential of the working electrode, which changes as the composition of the electrochemical cell changes, we can include an optional reference electrode and a high-impedance potentiometer.

Figure 11.4 Schematic diagram of a galvanostat: A is the auxiliary electrode; W is the working electrode; R is an optional reference electrode, E is a high-impedance potentiometer, and i is an ammeter. The working electrode and the optional reference electrode are connected to a ground.

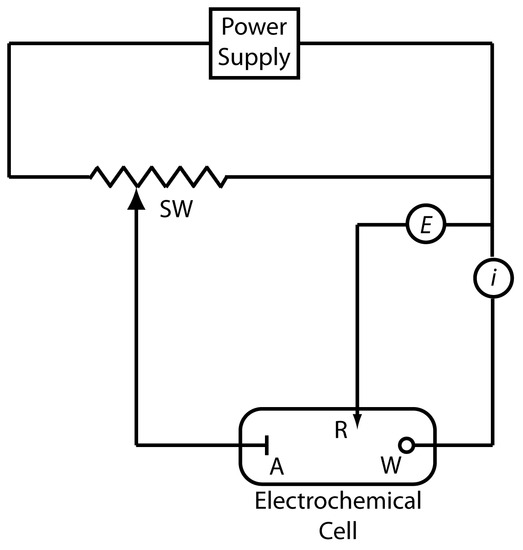
Potentiostats

A potentiostat allows us to control the potential of the working electrode. Figure 11.5 shows a schematic diagram for a manual potentiostat. The potential of the working electrode is measured relative to a constant-potential reference electrode that is connected to the working electrode through a high-impedance potentiometer. To set the working electrode’s potential we adjust the slide wire resistor, which is connected to the auxiliary electrode. If the working electrode’s potential begins to drift, we can adjust the slide wire resistor to return the potential to its initial value. The current flowing between the auxiliary electrode and the working electrode is measured with an ammeter. Modern potentiostats include waveform generators that allow us to apply a time-dependent potential profile, such as a series of potential pulses, to the working electrode.

Figure 11.5 Schematic diagram for a manual potentiostat: W is the working electrode; A is the auxiliary electrode; R is the reference electrode; SW is a slide-wire resistor, E is a high-impendance potentiometer; and i is an ammeter.

11.1.3 Interfacial Electrochemical Techniques

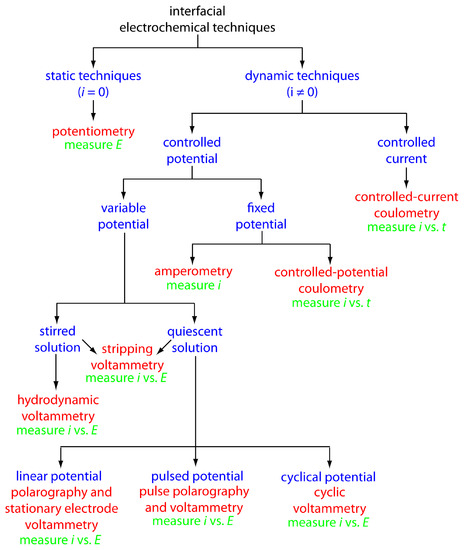
Because this chapter focuses on interfacial electrochemical techniques, let’s classify them into several categories. Figure 11.6 provides one version of a family tree highlighting the experimental conditions, the analytical signal, and the corresponding electrochemical techniques. Among the experimental conditions under our control are the potential or the current, and whether we stir the analyte’s solution.

At the first level, we divide interfacial electrochemical techniques into static techniques and dynamic techniques. In a static technique we do not allow current to pass through the analyte’s solution. Potentiometry, in which we measure the potential of an electrochemical cell under static conditions, is one of the most important quantitative electrochemical methods, and is discussed in detail in section 11.2.

Dynamic techniques, in which we allow current to flow through the analyte’s solution, comprise the largest group of interfacial electrochemical techniques. Coulometry, in which we measure current as a function of time, is covered in Section 11.3. Amperometry and voltammetry, in which we measure current as a function of a fixed or variable potential, is the subject of Section 11.4.

Figure 11.6 Family tree highlighting a number of interfacial electrochemical techniques. The specific techniques are shown in red, the experimental conditions are shown in blue, and the analytical signals are shown in green.

The material in this section—particularly the five important concepts—draws upon a vision for understanding electrochemistry outlined by Larry Faulkner in the article “Understanding Electrochemistry: Some Distinctive Concepts,” J. Chem. Educ. 1983, 60, 262–264. See also, Kissinger, P. T.; Bott, A. W. “Electrochemistry for the Non-Electrochemist,” Current Separations, 2002, 20:2, 51–53.

Contributors

David Harvey (DePauw University)