9.2: Acid–Base Titrations

Before 1800, most acid–base titrations used H₂SO₄, HCl, or HNO₃ as acidic titrants, and K₂CO₃ or Na₂CO₃ as basic titrants. A titration’s end point was determined using litmus as an indicator, which is red in acidic solutions and blue in basic solutions, or by the cessation of CO₂ effervescence when neutralizing CO₃^2–. Early examples of acid–base titrimetry include determining the acidity or alkalinity of solutions, and determining the purity of carbonates and alkaline earth oxides.

Three limitations slowed the development of acid–base titrimetry: the lack of a strong base titrant for the analysis of weak acids, the lack of suitable indicators, and the absence of a theory of acid–base reactivity. The introduction, in 1846, of NaOH as a strong base titrant extended acid–base titrimetry to the determination of weak acids. The synthesis of organic dyes provided many new indicators. Phenolphthalein, for example, was first synthesized by Bayer in 1871 and used as an indicator for acid–base titrations in 1877.

Despite the increasing availability of indicators, the absence of a theory of acid–base reactivity made it difficult to select an indicator. The development of equilibrium theory in the late 19th century led to significant improvements in the theoretical understanding of acid–base chemistry, and, in turn, of acid–base titrimetry. Sørenson’s establishment of the pH scale in 1909 provided a rigorous means for comparing indicators. The determination of acid–base dissociation constants made it possible to calculate a theoretical titration curve, as outlined by Bjerrum in 1914. For the first time analytical chemists had a rational method for selecting an indicator, establishing acid–base titrimetry as a useful alternative to gravimetry.

9.2.1 Acid–Base Titration Curves

In the overview to this chapter we noted that a titration’s end point should coincide with its equivalence point. To understand the relationship between an acid–base titration’s end point and its equivalence point we must know how the pH changes during a titration. In this section we will learn how to calculate a titration curve using the equilibrium calculations from Chapter 6. We also will learn how to quickly sketch a good approximation of any acid–base titration curve using a limited number of simple calculations.

Titrating Strong Acids and Strong Bases

For our first titration curve, let’s consider the titration of 50.0 mL of 0.100 M HCl using a titrant of 0.200 M NaOH. When a strong base and a strong acid react the only reaction of importance is

\[\mathrm{H_3O^+}(aq) + \mathrm{OH^-}(aq) \rightarrow \mathrm{2H_2O}(l) \tag{9.1}\]

Note

Although we have not written reaction 9.1 as an equilibrium reaction, it is at equilibrium; however, because its equilibrium constant is large—it is equal to (K_w)^–1 or 1.00 × 10¹⁴—we can treat reaction 9.1 as though it goes to completion.

Note

Step 1: Calculate the volume of titrant needed to reach the equivalence point.

The first task in constructing the titration curve is to calculate the volume of NaOH needed to reach the equivalence point, V_eq. At the equivalence point we know from reaction 9.1 that

\[\textrm{moles HCl = moles NaOH}\]

\[M_\textrm a \times V_\textrm a = M_\textrm b \times V_\textrm b\]

where the subscript ‘a’ indicates the acid, HCl, and the subscript ‘b’ indicates the base, NaOH. The volume of NaOH needed to reach the equivalence point is

\[V_\textrm{eq}=V_\textrm b=\dfrac{M_\textrm aV_\textrm a}{M_\textrm b}=\dfrac{(0.100\textrm{ M})(50.0\textrm{ mL})}{0.200\textrm{ M}}=25.0\textrm{ mL}\]

Note

Step 2: Calculate pH values before the equivalence point by determining the concentration of unreacted titrand.

Before the equivalence point, HCl is present in excess and the pH is determined by the concentration of unreacted HCl. At the start of the titration the solution is 0.100 M in HCl, which, because HCl is a strong acid, means that the pH is

\[\mathrm{pH = -\log[H_3O^+] = -\log[HCl] = -\log(0.100) = 1.00}\]

After adding 10.0 mL of NaOH the concentration of excess HCl is

\[\begin{align}
[\textrm{HCl}]&=\dfrac{\textrm{initial moles HCl} - \textrm{moles NaOH added}}{\textrm{total volume}}=\dfrac{M_\textrm aV_\textrm a - M_\textrm bV_\textrm b}{V_\textrm a + V_\textrm b}\\
&=\dfrac{(0.100\;\textrm M)(50.0\textrm{ mL}) - (0.200\;\textrm M)(10.0\textrm{ mL})}{50.0\textrm{ mL} + 10.0\textrm{ mL}} = 0.0500\;\textrm M
\end{align}\]

and the pH increases to 1.30.

Note

Step 3: The pH at the equivalence point for the titration of a strong acid with a strong base is 7.00.

At the equivalence point the moles of HCl and the moles of NaOH are equal. Since neither the acid nor the base is in excess, the pH is determined by the dissociation of water.

\[K_\textrm w = \mathrm{1.00\times10^{-14} = [H_3O^+][OH^-] = [H_3O^+]^2}\]

\[\mathrm{[H_3O^+] = 1.00\times10^{-7}\;M}\]

Thus, the pH at the equivalence point is 7.00.

Note

Step 4: Calculate pH values after the equivalence point by determining the concentration of excess titrant.

For volumes of NaOH greater than the equivalence point, the pH is determined by the concentration of excess OH^–. For example, after adding 30.0 mL of titrant the concentration of OH^– is

\[\begin{align}
[\textrm{OH}^-] &= \dfrac{\textrm{moles NaOH added} - \textrm{initial moles HCl}}{\textrm{total volume}}=\dfrac{M_\textrm bV_\textrm b-M_\textrm aV_\textrm a}{V_\textrm a+V_\textrm b}\\
&=\dfrac{(0.200\textrm{ M})(30.0\textrm{ mL}) - (0.100\textrm{ M})(50.0\textrm{ mL})}{50.0\textrm{ mL}+30.0\textrm{ mL}}=0.0125\textrm{ M}
\end{align}\]

To find the concentration of H₃O⁺ we use the K_w expression

\[[\mathrm{H_3O^+}]=\dfrac{K_\textrm w}{[\mathrm{OH^-}]}=\dfrac{1.00\times10^{-14}}{0.0125\textrm{ M}}=8.00\times10^{-13}\textrm{ M}\]

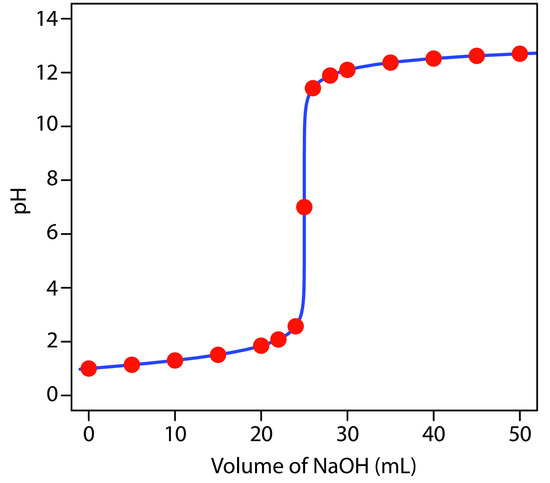
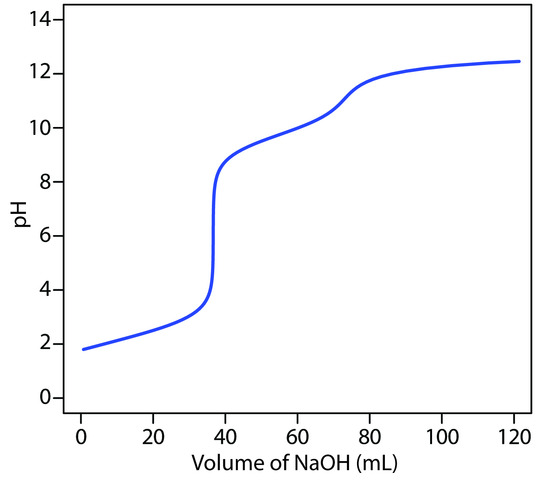
giving a pH of 12.10. Table 9.2 and Figure 9.6 show additional results for this titration curve. You can use this same approach to calculate the titration curve for the titration of a strong base with a strong acid, except the strong base is in excess before the equivalence point and the strong acid is in excess after the equivalence point.

Table 9.2 Titration of 50.0 mL of 0.100 M HCl with 0.200 M NaOH

Volume of NaOH (mL)	pH	Volume of NaOH (mL)	pH
0.00	1.00	26.0	11.42
5.00	1.14	28.0	11.89
10.0	1.30	30.0	12.10
15.0	1.51	35.0	12.37
20.0	1.85	40.0	12.52
22.0	2.08	45.0	12.62
24.0	2.57	50.0	12.70
25.0	7.00

Figure 9.6 Titration curve for the titration of 50.0 mL of 0.100 M HCl with 0.200 M NaOH. The red points correspond to the data in Table 9.2. The blue line shows the complete titration curve.

Practice Exercise 9.1

Construct a titration curve for the titration of 25.0 mL of 0.125 M NaOH with 0.0625 M HCl.

Click here to review your answer to this exercise.

Titrating a Weak Acid with a Strong Base

Note

Step 1: Calculate the volume of titrant needed to reach the equivalence point.

For this example, let’s consider the titration of 50.0 mL of 0.100 M acetic acid, CH₃COOH, with 0.200 M NaOH. Again, we start by calculating the volume of NaOH needed to reach the equivalence point; thus

\[\mathrm{moles\,CH_3COOH = moles\,NaOH}\]

\[M_\textrm a \times V_\textrm a = M_\textrm b \times V_\textrm b\]

\[V_\textrm{eq}= V_\textrm b= \dfrac{M_\textrm aV_\textrm a}{M_\textrm b}=\mathrm{\dfrac{(0.100\,M)(50.0\,mL)}{0.200\,M}}= 25.0\textrm{ mL}\]

Note

Step 2: Before adding the titrant, the pH is determined by the titrand, which in this case is a weak acid.

Before adding NaOH the pH is that for a solution of 0.100 M acetic acid. Because acetic acid is a weak acid, we calculate the pH using the method outlined in Chapter 6.

\[\mathrm{CH_3COOH}(aq)+\mathrm{H_2O}(l)\rightleftharpoons \mathrm{H_3O^+}(aq)+\mathrm{CH_3COO^-}(aq)\]

\[K_\textrm a=\mathrm{\dfrac{[H_3O^+][CH_3COO^-]}{[CH_3COOH]}}=\dfrac{(x)(x)}{0.100-x}=1.75\times10^{-5}\]

\[x=[\mathrm{H_3O^+}]=1.32\times10^{-3}\,\textrm M\]

At the beginning of the titration the pH is 2.88.

Adding NaOH converts a portion of the acetic acid to its conjugate base, CH₃COO^–.

\[\mathrm{CH_3COOH}(aq)+\mathrm{OH^-}(aq)\rightarrow \mathrm{H_2O}(l)+\mathrm{CH_3COO^-}(aq)\tag{9.2}\]

Note

Because the equilibrium constant for reaction 9.2 is quite large

\[K=K_\textrm a/K_\textrm w=1.75\times10^9\]

we can treat the reaction as if it goes to completion.

Any solution containing comparable amounts of a weak acid, HA, and its conjugate weak base, A^–, is a buffer. As we learned in Chapter 6, we can calculate the pH of a buffer using the Henderson–Hasselbalch equation.

\[\textrm{pH}=\textrm pK_\textrm a+\log\dfrac{[\textrm A^-]}{[\textrm{HA}]}\]

Note

Step 3: Before the equivalence point, the pH is determined by a buffer containing the titrand and its conjugate form.

Before the equivalence point the concentration of unreacted acetic acid is

\[\begin{align}
[\mathrm{CH_3COOH}]&=\dfrac{\textrm{initial moles }\mathrm{CH_3COOH} - \textrm{moles NaOH added}}{\textrm{total volume}}\\
&=\dfrac{M_\textrm aV_\textrm a-M_\textrm bV_\textrm b}{V_\textrm a+V_\textrm b}
\end{align}\]

and the concentration of acetate is

\[[\mathrm{CH_3COO^-}]=\dfrac{\textrm{moles NaOH added}}{\textrm{total volume}}=\dfrac{M_\textrm bV_\textrm b}{V_\textrm a+V_\textrm b}\]

For example, after adding 10.0 mL of NaOH the concentrations of CH₃COOH and CH₃COO^– are

\[\begin{align}
[\mathrm{CH_3COOH}]&=\dfrac{(0.100\textrm{ M})(50.0\textrm{ mL}) - (0.200\textrm{ M})(10.0\textrm{ mL})}{50.0\textrm{ mL}+10.0\textrm{ mL}}\\
&=0.0500\,\textrm M
\end{align}\]

\[[\mathrm{CH_3COO^-}]=\dfrac{\textrm{(0.200 M)(10.0 mL)}}{\textrm{50.0 mL + 10.0 mL}}=0.0333\;\textrm M\]

which gives us a pH of

\[\textrm{pH}=4.76+\log\dfrac{0.0333\textrm{ M}}{0.0500\textrm{ M}}=4.58\]

Note

Step 4: The pH at the equivalence point is determined by the titrand’s conjugate form, which in this case is a weak base.

At the equivalence point the moles of acetic acid initially present and the moles of NaOH added are identical. Because their reaction effectively proceeds to completion, the predominate ion in solution is CH₃COO^–, which is a weak base. To calculate the pH we first determine the concentration of CH₃COO^–

\[\begin{align}
[\mathrm{CH_3COO^-}]&=\dfrac{\textrm{moles NaOH added}}{\textrm{total volume}}\\
&=\dfrac{\textrm{(0.200 M)(25.0 mL)}}{\textrm{50.0 mL + 25.0 mL}}=0.0667\textrm{ M}
\end{align}\]

Note

Alternatively, we can calculate acetate’s concentration using the initial moles of acetic acid; thus

\[\begin{align}
[\mathrm{CH_3COO^-}]&=\dfrac{\textrm{initial moles }\mathrm{CH_3COOH}}{\textrm{total volume}}\\
&=\dfrac{(0.100\textrm{ M})(50.0\textrm{ mL})}{50.0\textrm{ mL}+25.0\textrm{ mL}}\\
&=0.0667\textrm{ M}
\end{align}\]

Next, we calculate the pH of the weak base as shown earlier in Chapter 6.

\[\mathrm{CH_3COO^-}(aq)+\mathrm{H_2O}(l)\rightleftharpoons \mathrm{OH^-}(aq)+\mathrm{CH_3COOH}(aq)\]

\[K_\textrm b=\dfrac{[\mathrm{OH^-}][\mathrm{CH_3COOH}]}{[\mathrm{CH_3COO^-}]} = \dfrac{(x)(x)}{0.0667-x} = 5.71\times10^{-10}\]

\[x=[\mathrm{OH^-}]=6.17\times10^{-6}\textrm{ M}\]

\[[\mathrm{H_3O^+}]=\dfrac{K_\textrm w}{[\mathrm{OH^-}]}=\dfrac{1.00\times10^{-14}}{6.17\times10^{-6}}=1.62\times10^{-9}\textrm{ M}\]

The pH at the equivalence point is 8.79.

Note

Step 5: Calculate pH values after the equivalence point by determining the concentration of excess titrant.

After the equivalence point, the titrant is in excess and the titration mixture is a dilute solution of NaOH. We can calculate the pH using the same strategy as in the titration of a strong acid with a strong base. For example, after adding 30.0 mL of NaOH the concentration of OH^– is

\[[\mathrm{OH^-}]=\dfrac{\textrm{(0.200 M)(30.0 mL)}-\textrm{(0.100 M)(50.0 mL)}}{\textrm{50.0 mL + 30.0 mL}}=0.0125\textrm{ M}\]

\[[\mathrm{H_3O^+}] = \dfrac{K_\textrm w}{[\mathrm{OH^-}]}=\dfrac{1.00\times10^{-14}}{0.0125\textrm{ M}} = 8.00\times10^{-13}\textrm{ M}\]

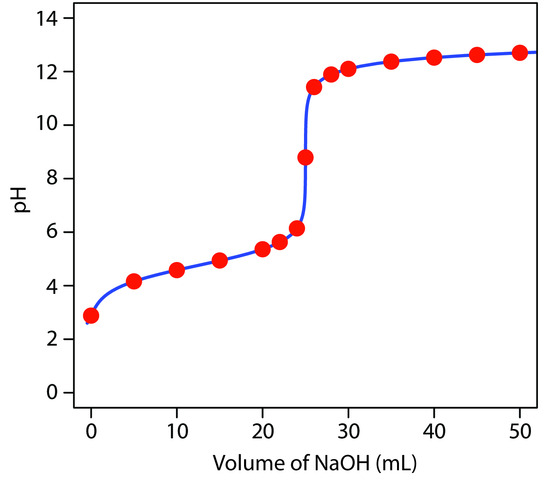
giving a pH of 12.10. Table 9.3 and Figure 9.7 show additional results for this titration. You can use this same approach to calculate the titration curve for the titration of a weak base with a strong acid, except the initial pH is determined by the weak base, the pH at the equivalence point by its conjugate weak acid, and the pH after the equivalence point by excess strong acid.

Table 9.3 Titration of 50.0 mL of 0.100 M Acetic Acid with 0.200 M NaOH

Volume of NaOH (mL)	pH	Volume of NaOH (mL)	pH
0.00	2.88	26.0	11.42
5.00	4.16	28.0	11.89
10.0	4.58	30.0	12.10
15.0	4.94	35.0	12.37
20.0	5.36	40.0	12.52
22.0	5.63	45.0	12.62
24.0	6.14	50.0	12.70
25.0	8.79

Figure 9.7 Titration curve for the titration of 50.0 mL of 0.100 M CH₃COOH with 0.200 M NaOH. The red points correspond to the data in Table 9.3. The blue line shows the complete titration curve.

Practice Exercise 9.2

Construct a titration curve for the titration of 25.0 mL of 0.125 M NH₃ with 0.0625 M HCl.

Click here to review your answer to this exercise.

We can extend our approach for calculating a weak acid–strong base titration curve to reactions involving multiprotic acids or bases, and mixtures of acids or bases. As the complexity of the titration increases, however, the necessary calculations become more time consuming. Not surprisingly, a variety of algebraic¹ and computer spreadsheet² approaches have been described to aid in constructing titration curves.

Sketching An Acid–Base Titration Curve

To evaluate the relationship between a titration’s equivalence point and its end point, we need to construct only a reasonable approximation of the exact titration curve. In this section we demonstrate a simple method for sketching an acid–base titration curve. Our goal is to sketch the titration curve quickly, using as few calculations as possible. Let’s use the titration of 50.0 mL of 0.100 M CH₃COOH with 0.200 M NaOH to illustrate our approach.

Note

This is the same example that we used in developing the calculations for a weak acid–strong base titration curve. You can review the results of that calculation in Table 9.3 and Figure 9.7.

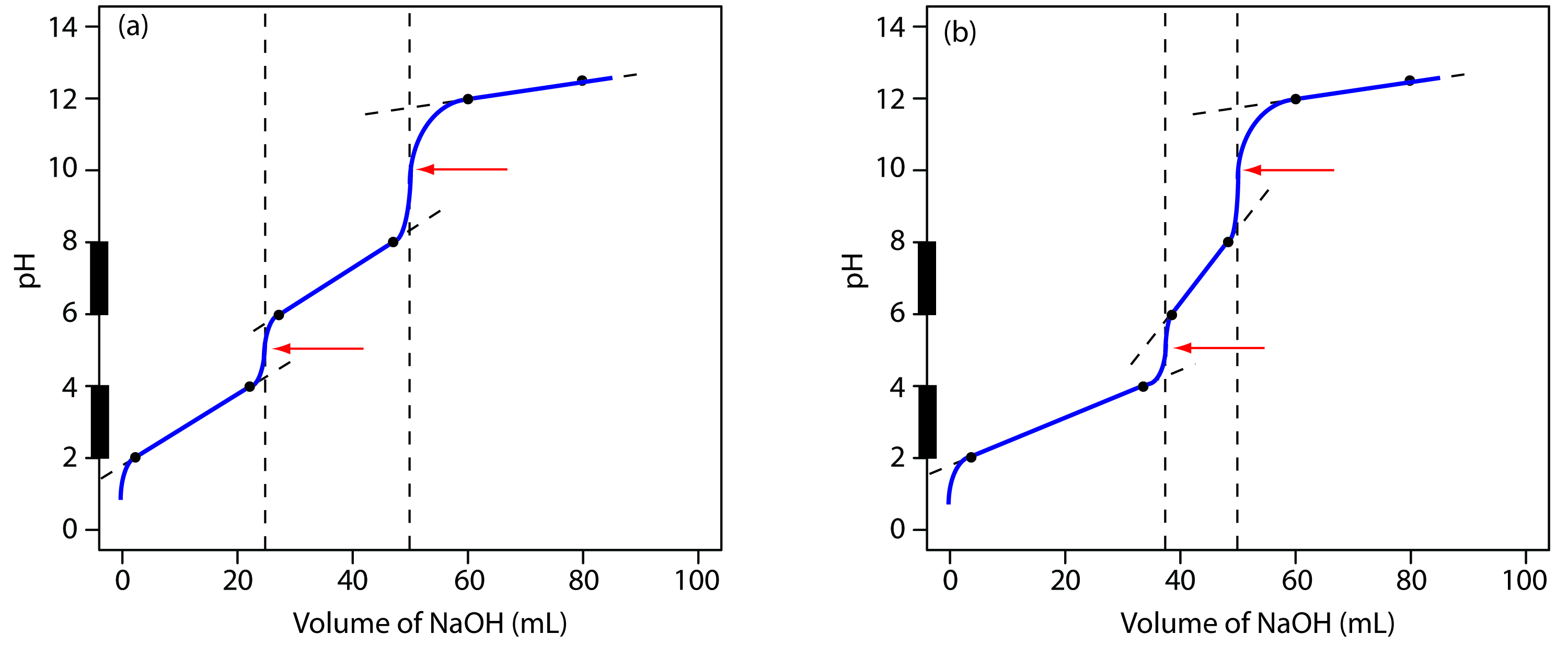
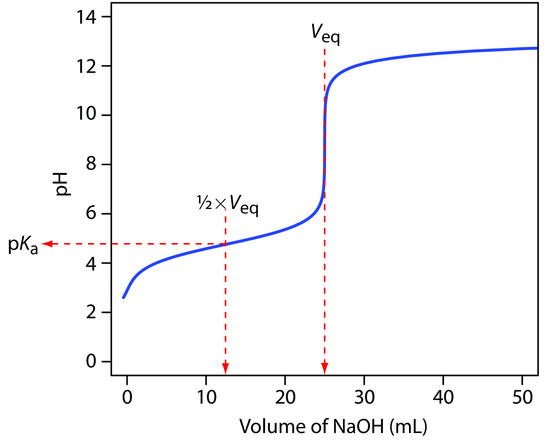
We begin by calculating the titration’s equivalence point volume, which, as we determined earlier, is 25.0 mL. Next we draw our axes, placing pH on the y-axis and the titrant’s volume on the x-axis. To indicate the equivalence point volume, we draw a vertical line corresponding to 25.0 mL of NaOH. Figure 9.8a shows the result of the first step in our sketch.

Figure 9.8 Illustrations showing the steps in sketching an approximate titration curve for the titration of 50.0 mL of 0.100 M CH₃COOH with 0.200 M NaOH: (a) locating the equivalence point volume; (b) plotting two points before the equivalence point; (c) plotting two points after the equivalence point; (d) preliminary approximation of titration curve using straight-lines; (e) final approximation of titration curve using a smooth curve; (f) comparison of approximate titration curve (solid black line) and exact titration curve (dashed red line). See the text for additional details.

Before the equivalence point the titration mixture’s pH is determined by a buffer of acetic acid, CH₃COOH, and acetate, CH₃COO^–. Although we can easily calculate a buffer’s pH using the Henderson–Hasselbalch equation, we can avoid this calculation by making a simple assumption. You may recall from Chapter 6 that a buffer operates over a pH range extending approximately ±1 pH unit on either side of the weak acid’s pK_a value. The pH is at the lower end of this range, pH = pK_a – 1, when the weak acid’s concentration is 10× greater than that of its conjugate weak base. The buffer reaches its upper pH limit, pH = pK_a + 1, when the weak acid’s concentration is 10× smaller than that of its conjugate weak base. When titrating a weak acid or a weak base, the buffer spans a range of volumes from approximately 10% of the equivalence point volume to approximately 90% of the equivalence point volume.

Figure 9.8b shows the second step in our sketch. First, we superimpose acetic acid’s ladder diagram on the y-axis, including its buffer range, using its pK_a value of 4.76. Next, we add points representing the pH at 10% of the equivalence point volume (a pH of 3.76 at 2.5 mL) and at 90% of the equivalence point volume (a pH of 5.76 at 22.5 mL).

Note

The actual values are 9.09% and 90.9%, but for our purpose, using 10% and 90% is more convenient; that is, after all, one advantage of an approximation! Problem 9.4 in the end-of-chapter problems asks you to verify these percentages.

The third step in sketching our titration curve is to add two points after the equivalence point. The pH after the equivalence point is fixed by the concentration of excess titrant, NaOH. Calculating the pH of a strong base is straightforward, as we have seen earlier. Figure 9.8c shows the pH after adding 30.0 mL and 40.0 mL of NaOH.

Note

See Table 9.3 for the values.

Next, we draw a straight line through each pair of points, extending the lines through the vertical line representing the equivalence point’s volume (Figure 9.8d). Finally, we complete our sketch by drawing a smooth curve that connects the three straight-line segments (Figure 9.8e). A comparison of our sketch to the exact titration curve (Figure 9.8f) shows that they are in close agreement.

Practice Exercise 9.3

Sketch a titration curve for the titration of 25.0 mL of 0.125 M NH₃ with 0.0625 M HCl and compare to the result from Practice Exercise 9.2.

Click here to review your answer to this exercise.

As shown by the following example, we can adapt this approach to acid–base titrations, including those involving polyprotic weak acids and bases, or mixtures of weak acids and bases.

Example 9.1

Sketch titration curves for the following two systems: (a) the titration of 50.0 mL of 0.050 M H₂A, a diprotic weak acid with a pK_a1 of 3 and a pK_a2 of 7; and (b) the titration of a 50.0 mL mixture containing 0.075 M HA, a weak acid with a pK_a of 3, and 0.025 M HB, a weak acid with a pK_a of 7. For both titrations the titrant is 0.10 M NaOH.

Solution

Figure 9.9a shows the titration curve for H₂A, including the ladder diagram on the y-axis, the equivalence points at 25.0 mL and 50.0 mL, two points before each equivalence point, two points after the last equivalence point, and the straight-lines that help in sketching the final curve. Before the first equivalence point the pH is controlled by a buffer consisting of H₂A and HA^–. An HA^–/A^2– buffer controls the pH between the two equivalence points. After the second equivalence point the pH reflects the concentration of excess NaOH.

Figure 9.9b shows the titration curve for the mixture of HA and HB. Again, there are two equivalence points. In this case, however, the equivalence points are not equally spaced because the concentration of HA is greater than that for HB. Since HA is the stronger of the two weak acids it reacts first; thus, the pH before the first equivalence point is controlled by a buffer consisting of HA and A^–. Between the two equivalence points the pH reflects the titration of HB and is determined by a buffer consisting of HB and B^–. After the second equivalence point excess NaOH is responsible for the pH.

Figure 9.9 Titration curves for Example 9.1. The red arrows show the locations of the equivalence points.

Practice Exercise 9.4

Sketch the titration curve for 50.0 mL of 0.050 M H₂A, a diprotic weak acid with a pK_a1 of 3 and a pK_a2 of 4, using 0.100 M NaOH as the titrant. The fact that pK_a2 falls within the buffer range of pK_a1 presents a challenge that you will need to consider.
Click here to review your answer to this exercise.

9.2.2 Selecting and Evaluating the End point

Earlier we made an important distinction between a titration’s end point and its equivalence point. The difference between these two terms is important and deserves repeating. An equivalence point, which occurs when we react stoichiometrically equal amounts of the analyte and the titrant, is a theoretical not an experimental value. A titration’s end point is an experimental result, representing our best estimate of the equivalence point. Any difference between an equivalence point and its corresponding end point is a source of determinate error. It is even possible that an equivalence point does not have a useful end point.

Where is The Equivalence Point?

Earlier we learned how to calculate the pH at the equivalence point for the titration of a strong acid with a strong base, and for the titration of a weak acid with a strong base. We also learned to quickly sketch a titration curve with only a minimum of calculations. Can we also locate the equivalence point without performing any calculations. The answer, as you might guess, is often yes!

For most acid–base titrations the inflection point, the point on a titration curve having the greatest slope, very nearly coincides with the equivalence point.³ The red arrows in Figure 9.9, for example, indicate the equivalence points for the titration curves from Example 9.1. An inflection point actually precedes its corresponding equivalence point by a small amount, with the error approaching 0.1% for weak acids or weak bases with dissociation constants smaller than 10^–9, or for very dilute solutions.

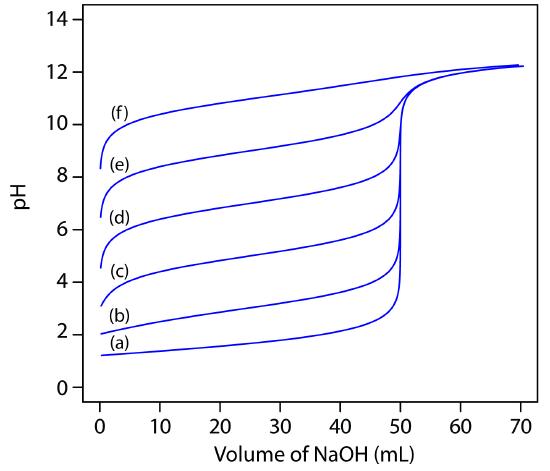
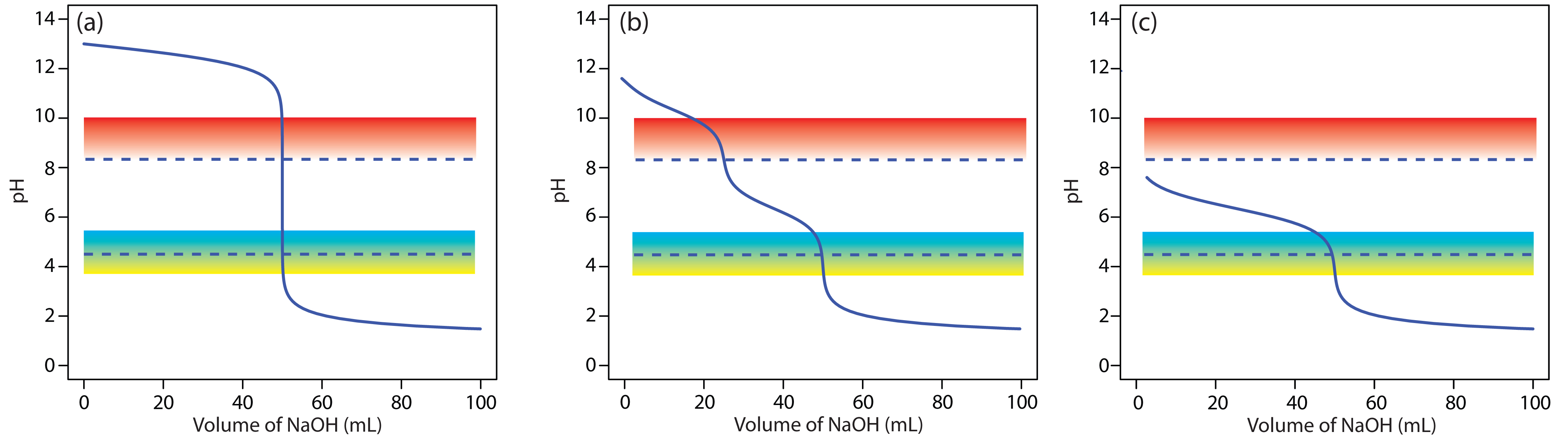
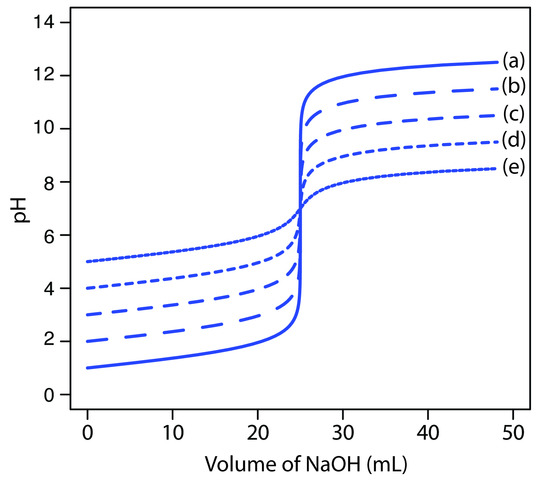
The principal limitation to using an inflection point to locate the equivalence point is that the inflection point must be present. For some titrations the inflection point may be missing or difficult to find. Figure 9.10, for example, demonstrates the affect of a weak acid’s dissociation constant, K_a, on the shape of titration curve. An inflection point is visible, even if barely so, for acid dissociation constants larger than 10^–9, but is missing when K_a is 10^–11.

Figure 9.10 Weak acid–strong base titration curves for the titration of 50.0 mL of 0.100 M HA with 0.100 M NaOH. The pK_a values for HA are (a) 1, (b) 3, (c) 5, (d) 7, (e) 9, and (f) 11.

An inflection point also may be missing or difficult to detect if the analyte is a multiprotic weak acid or weak base with successive dissociation constants that are similar in magnitude. To appreciate why this is true let’s consider the titration of a diprotic weak acid, H₂A, with NaOH. During the titration the following two reactions occur.

\[\mathrm{H_2A}(aq)+\mathrm{OH^-}(aq) \rightarrow \mathrm{HA^-}(aq)+\mathrm{H_2O}(l)\tag{9.3}\]

\[\mathrm{HA^-}(aq)+\mathrm{OH^-}(aq) \rightarrow \mathrm{A^{2-}}(aq)+\mathrm{H_2O}(l)\tag{9.4}\]

To see two distinct inflection points, reaction 9.3 must be essentially complete before reaction 9.4 begins.

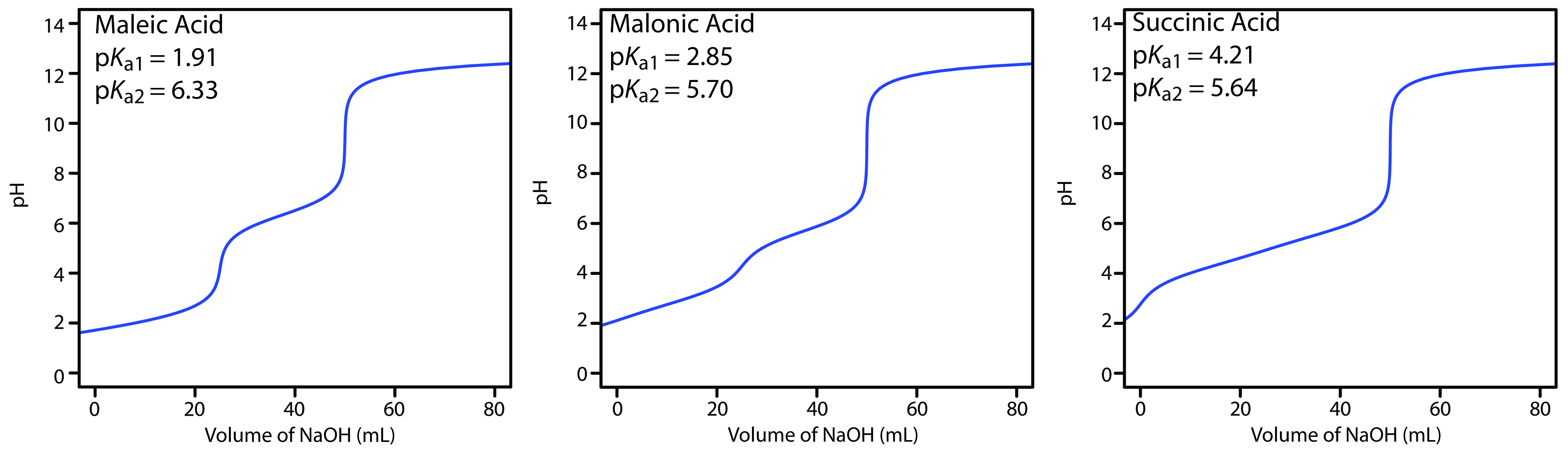
Figure 9.11 shows titration curves for three diprotic weak acids. The titration curve for maleic acid, for which K_a1 is approximately 20,000× larger than K_a2, has two distinct inflection points. Malonic acid, on the other hand, has acid dissociation constants that differ by a factor of approximately 690. Although malonic acid’s titration curve shows two inflection points, the first is not as distinct as that for maleic acid. Finally, the titration curve for succinic acid, for which the two K_a values differ by a factor of only 27, has only a single inflection point corresponding to the neutralization of HC₄H₄O₄^– to C₄H₄O₄^2–. In general, we can detect separate inflection points when successive acid dissociation constants differ by a factor of at least 500 (a ∆pK_a of at least 2.7).

Figure 9.11 Titration curves for the diprotic weak acids maleic acid, malonic acid, and succinic acid. Each titration curve is for 50.0 mL of 0.0500 M weak acid using 0.100 M NaOH. Although each titration curve has equivalence points at 25.0 mL and 50.0 mL of NaOH, the titration curve for succinic acid shows only one inflection point.

Finding the End point with an Indicator

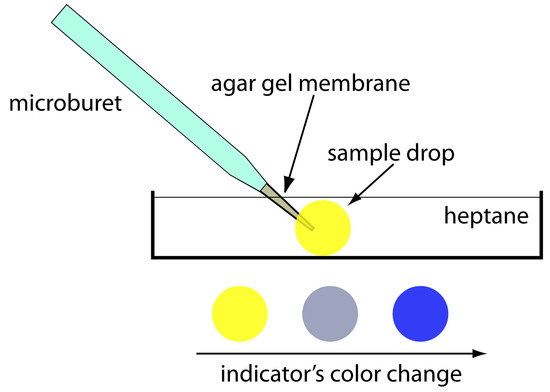
One interesting group of weak acids and weak bases are organic dyes. Because an organic dye has at least one highly colored conjugate acid–base species, its titration results in a change in both pH and color. We can use this change in color to indicate the end point of a titration, provided that it occurs at or near the titration’s equivalence point.

Let’s use an indicator, HIn, to illustrate how an acid–base indicator works. Because the indicator’s acid and base forms have different colors—the weak acid, HIn, is yellow and the weak base, In^–, is red—the color of a solution containing the indicator depends on their relative concentrations. The indicator’s acid dissociation reaction

\[\mathrm{HIn}(aq)+\mathrm{H_2O}(l) \rightleftharpoons \mathrm{H_3O^+}(aq)+\mathrm{In^-}(aq)\]

has an equilibrium constant of

\[K_\textrm a=\dfrac{[\mathrm{H_3O^+}][\mathrm{In^-}]}{[\mathrm{HIn}]}\tag{9.5}\]

Taking the negative log of each side of equation 9.5, and rearranging to solve for pH leaves with a equation

\[\textrm{pH}=\textrm pK_\textrm a+\log\dfrac{[\mathrm{In^-}]}{[\mathrm{HIn}]}\tag{9.6}\]

relating the solution’s pH to the relative concentrations of HIn and In^–.

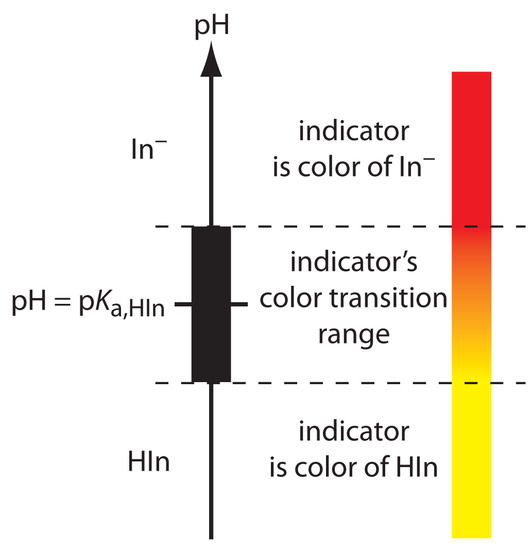
If we can detect HIn and In^– with equal ease, then the transition from yellow to red (or from red to yellow) reaches its midpoint, which is orange, when their concentrations are equal, or when the pH is equal to the indicator’s pK_a. If the indicator’s pK_a and the pH at the equivalence point are identical, then titrating until the indicator turns orange is a suitable end point. Unfortunately, we rarely know the exact pH at the equivalence point. In addition, determining when the concentrations of HIn and In^– are equal may be difficult if the indicator’s change in color is subtle.

We can establish the range of pHs over which the average analyst observes a change in the indicator’s color by making the following assumptions—the indicator’s color is yellow if the concentration of HIn is 10× greater than that of In^–, and its color is red if the concentration of HIn is 10× smaller than that of In^–. Substituting these inequalities into equation 9.6

\[\textrm{pH}=\textrm pK_\textrm a+\log\dfrac{1}{10}=\textrm pK_\textrm a-1\]

\[\textrm{pH}=\textrm pK_\textrm a+\log\dfrac{10}{1}=\textrm pK_\textrm a+1\]

shows that the indicator changes color over a pH range extending ±1 unit on either side of its pK_a. As shown in Figure 9.12, the indicator is yellow when the pH is less than pK_a – 1, and it is red for pHs greater than pK_a + 1. For pHs between pK_a – 1 and pK_a + 1 the indicator’s color passes through various shades of orange. The properties of several common acid–base indicators are shown in Table 9.4.

Figure 9.12 Diagram showing the relationship between pH and an indicator’s color. The ladder diagram defines pH values where HIn and In^– are the predominate species. The indicator changes color when the pH is between pKa – 1 and pKa + 1.

Table 9.4 Properties of Selected Acid–Base Indicators

Indicator	Acid Color	Base Color	pH Range	pKa
cresol red	red	yellow	0.2–1.8	–
thymol blue	red	yellow	1.2–2.8	1.7
bromophenol blue	yellow	blue	3.0–4.6	4.1
methyl orange	red	yellow	3.1–4.4	3.7
Congo red	blue	red	3.0–5.0	–
bromocresol green	yellow	blue	3.8–5.4	4.7
methyl red	red	yellow	4.2–6.3	5.0
bromocresol purple	yellow	purple	5.2–6.8	6.1
litmus	red	blue	5.0–8.0	–
bromothymol blue	yellow	blue	6.0–7.6	7.1
phenol red	yellow	blue	6.8–8.4	7.8
cresol red	yellow	red	7.2–8.8	8.2
thymol blue	yellow	red	8.0–9.6	8.9
phenolphthalein	colorless	red	8.3–10.0	9.6
alizarin yellow R	yellow	orange–red	10.1–12.0	–

Note

You may wonder why an indicator’s pH range, such as that for phenolphthalein, is not equally distributed around its pK_a value. The explanation is simple. Figure 9.12 presents an idealized view of an indicator in which our sensitivity to the indicator’s two colors is equal. For some indicators only the weak acid or the weak base is colored. For other indicators both the weak acid and the weak base are colored, but one form is easier to see. In either case, the indicator’s pH range is skewed in the direction of the indicator’s less colored form. Thus, phenolphthalein’s pH range is skewed in the direction of its colorless form, shifting the pH range to values lower than those suggested by Figure 9.12.

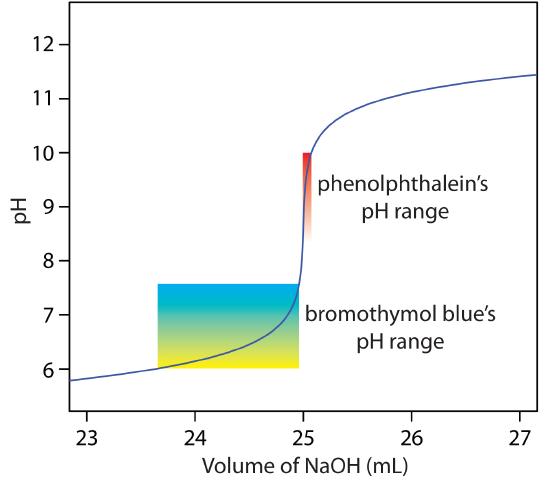
The relatively broad range of pHs over which an indicator changes color places additional limitations on its feasibility for signaling a titration’s end point. To minimize a determinate titration error, an indicator’s entire pH range must fall within the rapid change in pH at the equivalence point. For example, in Figure 9.13 we see that phenolphthalein is an appropriate indicator for the titration of 50.0 mL of 0.050 M acetic acid with 0.10 M NaOH. Bromothymol blue, on the other hand, is an inappropriate indicator because its change in color begins before the initial sharp rise in pH, and, as a result, spans a relatively large range of volumes. The early change in color increases the probability of obtaining inaccurate results, while the range of possible end point volumes increases the probability of obtaining imprecise results.

Figure 9.13 Portion of the titration curve for 50.0 mL of 0.050 M CH₃COOH with 0.10 M NaOH, highlighting the region containing the equivalence point. The end point transitions for the indicators phenolphthalein and bromothymol blue are superimposed on the titration curve.

Practice Exercise 9.5

Suggest a suitable indicator for the titration of 25.0 mL of 0.125 M NH₃ with 0.0625 M NaOH. You constructed a titration curve for this titration in Practice Exercise 9.2 and Practice Exercise 9.3.

Click here to review your answer to this exercise.

Finding the End point by Monitoring pH

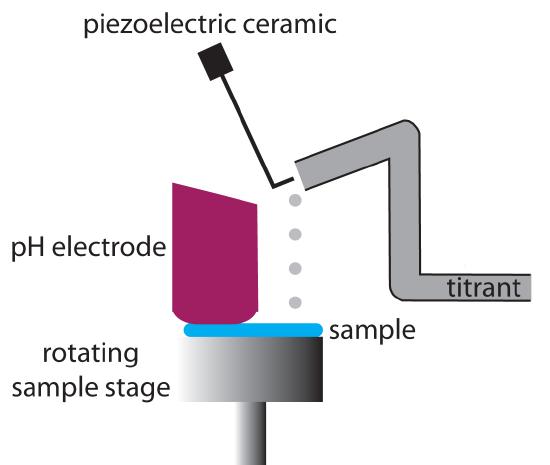
An alternative approach for locating a titration’s end point is to continuously monitor the titration’s progress using a sensor whose signal is a function of the analyte’s concentration. The result is a plot of the entire titration curve, which we can use to locate the end point with a minimal error.

The obvious sensor for monitoring an acid–base titration is a pH electrode and the result is a potentiometric titration curve. (See Chapter 11 for more details about pH electrodes.) For example, Figure 9.14a shows a small portion of the potentiometric titration curve for the titration of 50.0 mL of 0.050 M CH₃COOH with 0.10 M NaOH, focusing on the region containing the equivalence point. The simplest method for finding the end point is to locate the titration curve’s inflection point, as shown by the arrow. This is also the least accurate method, particularly if the titration curve has a shallow slope at the equivalence point.

Figure 9.14 Titration curves for the titration of 50.0 mL of 0.050 M CH₃COOH with 0.10 M NaOH: (a) normal titration curve; (b) first derivative titration curve; (c) second derivative titration curve; (d) Gran plot. The red arrow shows the location of the titration’s end point.

Another method for locating the end point is to plot the titration curve’s first derivative, which gives the titration curve’s slope at each point along the x-axis. Examine Figure 9.14a and consider how the titration curve’s slope changes as we approach, reach, and pass the equivalence point. Because the slope reaches its maximum value at the inflection point, the first derivative shows a spike at the equivalence point (Figure 9.14b).

The second derivative of a titration curve may be more useful than the first derivative because the equivalence point intersects the volume axis. Figure 9.14c shows the resulting titration curve.

Derivative methods are particularly useful when titrating a sample that contains more than one analyte. If we rely on indicators to locate the end points, then we usually must complete separate titrations for each analyte. If we record the titration curve, however, then a single titration is sufficient. The precision with which we can locate the end point also makes derivative methods attractive for an analyte with a poorly defined normal titration curve.

Derivative methods work well only if we record sufficient data during the rapid increase in pH near the equivalence point. This is usually not a problem if we use an automatic titrator, such as that seen earlier in Figure 9.5. Because the pH changes so rapidly near the equivalence point—a change of several pH units with the addition of several drops of titrant is not unusual—a manual titration does not provide enough data for a useful derivative titration curve. A manual titration does contain an abundance of data during the more gently rising portions of the titration curve before and after the equivalence point. This data also contains information about the titration curve’s equivalence point.

Note

Suppose we have the following three points on our titration curve:

volume (mL)	pH
23.65	6.00
23.91	6.10
24.13	6.20

Mathematically, we can approximate the first derivative as ∆pH/∆V, where ∆pH is the change in pH between successive additions of titrant. Using the first two points, the first derivative is

\[\dfrac{\Delta \textrm{pH}}{\Delta V}=\dfrac{6.10 - 6.00}{23.91 - 23.65}=0.385\]

which we assign to the average of the two volumes, or 23.78 mL. For the second and third points, the first derivative is 0.455 and the average volume is 24.02 mL.

volume (mL)	∆pH/∆V
23.78	0.385
24.02	0.455

We can approximate the second derivative as ∆(∆pH/∆V)/∆V, or ∆²pH/∆V². Using the two points from our calculation of the first derivative, the second derivative is

\[\dfrac{\Delta^2 \textrm{pH}}{\Delta V^2}=\dfrac{0.455-0.385}{23.78-24.02}=0.292\]

Note that calculating the first derivative comes at the expense of losing one piece of information (three points become two points), and calculating the second derivative comes at the expense of losing two pieces of information.

Consider again the titration of acetic acid, CH₃COOH, with NaOH. At any point during the titration acetic acid is in equilibrium with H₃O⁺ and CH₃COO^–

\[\mathrm{CH_3COOH}(aq)+\mathrm{H_2O}(l)\rightleftharpoons \mathrm{H_3O^+}(aq)+\mathrm{CH_3COO^-}(aq)\]

for which the equilibrium constant is

\[K_\textrm a=\dfrac{[\mathrm{H_3O^+}][\mathrm{CH_3COO^-}]}{[\mathrm{CH_3COOH}]}\]

Before the equivalence point the concentrations of CH₃COOH and CH₃COO^– are

\[\begin{align}
[\mathrm{CH_3COOH}]&=\dfrac{\textrm{initial moles }\mathrm{CH_3COOH}-\textrm{moles NaOH added}}{\textrm{total volume}}\\
&=\dfrac{M_\textrm aV_\textrm a-M_\textrm bV_\textrm b}{V_\textrm a+V_\textrm b}
\end{align}\]

\[[\mathrm{CH_3COO^-}]=\dfrac{\textrm{moles NaOH added}}{\textrm{total volume}}= \dfrac{M_\textrm bV_\textrm b}{V_\textrm a+V_\textrm b}\]

Substituting these equations into the K_a expression and rearranging leaves us with

\[K_\textrm a=\dfrac{[\mathrm{H_3O^+}](M_\textrm bV_\textrm b)}{M_\textrm aV_\textrm a-M_\textrm bV_\textrm b}\]

\[K_\textrm aM_\textrm aV_\textrm a-K_\textrm aM_\textrm bV_\textrm b=[\mathrm{H_3O^+}](M_\textrm bV_\textrm b)\]

\[\dfrac{K_\textrm aM_\textrm aV_\textrm a}{M_\textrm b}-K_\textrm aV_\textrm b=[\mathrm{H_3O^+}]\times V_\textrm b\]

Finally, recognizing that the equivalence point volume is

\[V_\textrm{eq}=\dfrac{M_\textrm aV_\textrm a}{M_\textrm b}\]

leaves us with the following equation.

\[[\mathrm{H_3O^+}]\times V_\textrm b = K_\textrm aV_\textrm{eq}-K_\textrm aV_\textrm b\]

For volumes of titrant before the equivalence point, a plot of V_b×[H₃O⁺] versus V_b is a straight-line with an x-intercept of V_eq and a slope of –K_a. Figure 9.14d shows a typical result. This method of data analysis, which converts a portion of a titration curve into a straight-line, is a Gran plot.

Finding the End point by Monitoring Tempmperature

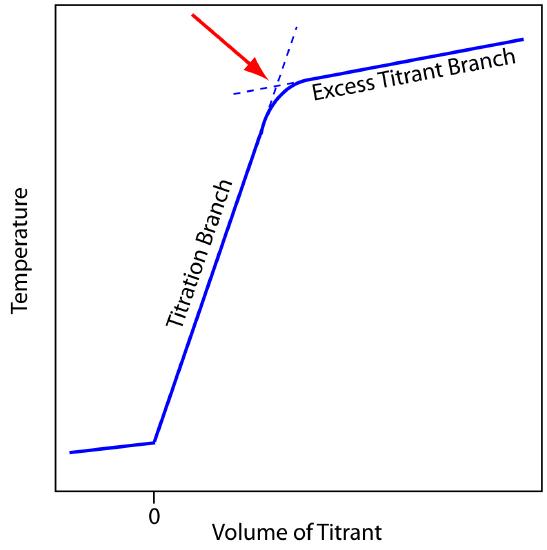
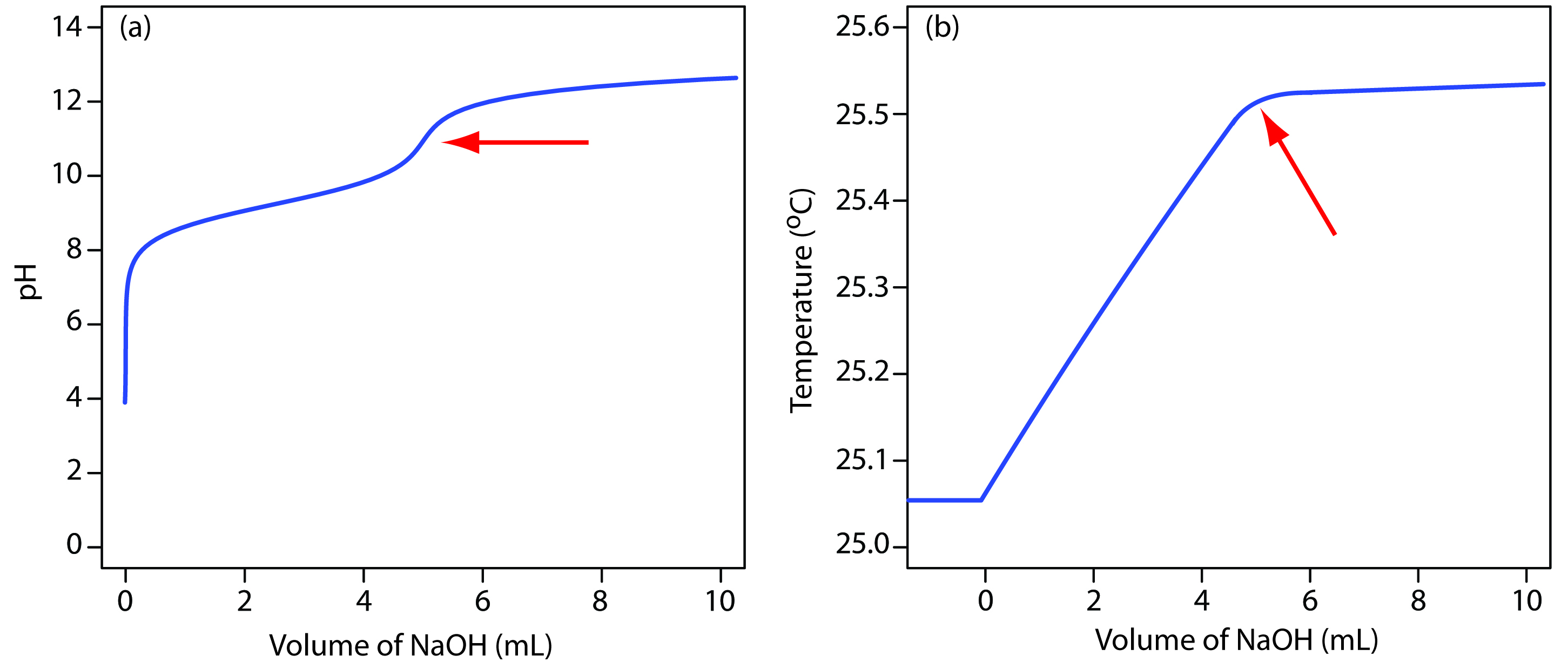
The reaction between an acid and a base is exothermic. Heat generated by the reaction is absorbed by the titrand, increasing its temperature. Monitoring the titrand’s temperature as we add the titrant provides us with another method for recording a titration curve and identifying the titration’s end point (Figure 9.15).

Figure 9.15 Typical thermometric titration curve. The endpoint, shown by the red arrow, is found by extrapolating the titration branch and the excess titration branch.

Before adding titrant, any change in the titrand’s temperature is the result of warming or cooling as it equilibrates with the surroundings. Adding titrant initiates the exothermic acid–base reaction, increasing the titrand’s temperature. This part of a thermometric titration curve is called the titration branch. The temperature continues to rise with each addition of titrant until we reach the equivalence point. After the equivalence point, any change in temperature is due to the titrant’s enthalpy of dilution, and the difference between the temperatures of the titrant and titrand. Ideally, the equivalence point is a distinct intersection of the titration branch and the excess titrant branch. As shown in Figure 9.15, however, a thermometric titration curve usually shows curvature near the equivalence point due to an incomplete neutralization reaction, or to the excessive dilution of the titrand and the titrant during the titration. The latter problem is minimized by using a titrant that is 10–100 times more concentrated than the analyte, although this results in a very small end point volume and a larger relative error. If necessary, the end point is found by extrapolation.

Although not a particularly common method for monitoring acid–base titrations, a thermometric titration has one distinct advantage over the direct or indirect monitoring of pH. As discussed earlier, the use of an indicator or the monitoring of pH is limited by the magnitude of the relevant equilibrium constants. For example, titrating boric acid, H₃BO₃, with NaOH does not provide a sharp end point when monitoring pH because boric acid’s K_a of 5.8 × 10^–10 is too small (Figure 9.16a). Because boric acid’s enthalpy of neutralization is fairly large, –42.7 kJ/mole, however, its thermometric titration curve provides a useful endpoint (Figure 9.16b).

Figure 9.16 Titration curves for the titration of 50.0 mL of 0.050 M H₃BO₃ with 0.50 M NaOH obtained by monitoring (a) pH, and (b) temperature. The red arrows show the end points for the titrations.

9.2.3 Titrations in Nonaqueous Solvents

Thus far we have assumed that the titrant and the titrand are aqueous solutions. Although water is the most common solvent in acid–base titrimetry, switching to a nonaqueous solvent can improve a titration’s feasibility.

For an amphoteric solvent, SH, the autoprotolysis constant, K_s, relates the concentration of its protonated form, SH₂⁺, to that of its deprotonated form, S^–

\[\mathrm{2SH}\rightleftharpoons \mathrm{SH_2^+}+\mathrm{S^-}\]

\[K_\textrm s = [\mathrm{SH_2^+}][\mathrm{S^-}]\]

and the solvent’s pH and pOH are

\[\textrm{pH}=-\log[\mathrm{SH_2^+}]\]

\[\textrm{pOH}=-\log[\mathrm{S^-}]\]

Note

You should recognize that K_w is just specific form of K_s when the solvent is water.

The most important limitation imposed by K_s is the change in pH during a titration. To understand why this is true, let’s consider the titration of 50.0 mL of 1.0×10^–4 M HCl using 1.0×10^–4 M NaOH. Before the equivalence point, the pH is determined by the untitrated strong acid. For example, when the volume of NaOH is 90% of V_eq, the concentration of H₃O⁺ is

\[\begin{align}
[\mathrm{H_3O^+}]&=\dfrac{M_\textrm aV_\textrm a-M_\textrm bV_\textrm b}{V_\textrm a+V_\textrm b}\\
&=\dfrac{\mathrm{(1.0\times10^{-4}\;M)(50.0\;mL)}-(\mathrm{1.0\times10^{-4}\;M)(45.0\;mL)}}{\textrm{50.0 mL + 45.0 mL}}\\
&=5.3\times10^{-6}\textrm{ M}
\end{align}\]

Note

The titration’s equivalence point requires 50.0 mL of NaOH; thus, 90% of V_eq is 45.0 mL of NaOH.

and the pH is 5.3. When the volume of NaOH is 110% of V_eq, the concentration of OH^– is

\[\begin{align}
[\mathrm{OH^-}]&=\dfrac{M_\textrm bV_\textrm b-M_\textrm aV_\textrm a}{V_\textrm a+V_\textrm b}\\
&=\dfrac{(1.0\times10^{-4}\textrm{ M})(55.0\textrm{ mL})-(1.0\times10^{-4} \textrm{ M})(50.0\textrm{ mL})}{\textrm{50.0 mL + 55.0 mL}}\\
&=4.8\times10^{-6}\textrm{ M}
\end{align}\]

Note

The titration’s equivalence point requires 50.0 mL of NaOH; thus, 110% of V_eq is 55.0 mL of NaOH.

and the pOH is 5.3. The titrand’s pH is

\[\textrm{pH}=\textrm pK_\textrm w-\textrm{pOH}=14-5.3=8.7\]

and the change in the titrand’s pH as the titration goes from 90% to 110% of V_eq is

\[\Delta\textrm{pH} = 8.7 - 5.3 = 3.4\]

If we carry out the same titration in a nonaqueous solvent with a K_s of 1.0×10^–20, the pH after adding 45.0 mL of NaOH is still 5.3. However, the pH after adding 55.0 mL of NaOH is

\[\textrm{pH}=\textrm pK_\textrm s-\textrm{pOH}=20-5.3=14.7\]

In this case the change in pH

\[\Delta\mathrm{pH}=14.7-5.3=9.4\]

is significantly greater than that obtained when the titration is carried out in water. Figure 9.17 shows the titration curves in both the aqueous and the nonaqueous solvents.

Figure 9.17 Titration curves for 50.0 mL of 1.0 × 10^–4 M HCl using 1.0 × 10^–4 M NaOH in (a) water, K_w = 1.0 × 10^–14, and (b) a nonaqueous solvent, K_s = 1.0 × 10^–20.

Another parameter affecting the feasibility of an acid–base titration is the titrand’s dissociation constant. Here, too, the solvent plays an important role. The strength of an acid or a base is a relative measure of the ease transferring a proton from the acid to the solvent, or from the solvent to the base. For example, HF, with a K_a of 6.8 × 10^–4, is a better proton donor than CH₃COOH, for which K_a is 1.75 × 10^–5.

The strongest acid that can exist in water is the hydronium ion, H₃O⁺. HCl and HNO₃ are strong acids because they are better proton donors than H₃O⁺ and essentially donate all their protons to H₂O, leveling their acid strength to that of H₃O⁺. In a different solvent HCl and HNO₃ may not behave as strong acids.

If we place acetic acid in water the dissociation reaction

\[\mathrm{CH_3COOH}(aq)+\mathrm{H_2O}(l)\rightleftharpoons \mathrm{H_3O^+}(aq)+\mathrm{CH_3COO^-}(aq)\]

does not proceed to a significant extent because CH₃COO^– is a stronger base than H₂O, and H₃O⁺ is a stronger acid than CH₃COOH. If we place acetic acid in a solvent, such as ammonia, that is a stronger base than water, then the reaction

\[\mathrm{CH_3COOH}+\mathrm{NH_3}\rightleftharpoons \mathrm{NH_4^+}+\mathrm{CH_3COO^-}\]

proceeds to a greater extent. In fact, both HCl and CH₃COOH are strong acids in ammonia.

All other things being equal, the strength of a weak acid increases if we place it in a solvent that is more basic than water, and the strength of a weak base increases if we place it in a solvent that is more acidic than water. In some cases, however, the opposite effect is observed. For example, the pK_b for NH₃ is 4.75 in water and it is 6.40 in the more acidic glacial acetic acid. In contradiction to our expectations, NH₃ is a weaker base in the more acidic solvent. A full description of the solvent’s effect on the pK_a of weak acid or the pK_b of a weak base is beyond the scope of this text. You should be aware, however, that a titration that is not feasible in water may be feasible in a different solvent.

Note

The best way to appreciate the theoretical and practical details discussed in this section is to carefully examine a typical acid–base titrimetric method. Although each method is unique, the following description of the determination of protein in bread provides an instructive example of a typical procedure. The description here is based on Method 13.86 as published in Official Methods of Analysis, 8th Ed., Association of Official Agricultural Chemists: Washington, D. C., 1955.

Representative Method 9.1

Determination of Protein in Bread

Description of the Method

This method is based on a determination of %w/w nitrogen using the Kjeldahl method. The protein in a sample of bread is oxidized to NH₄⁺ using hot concentrated H₂SO₄. After making the solution alkaline, which converts the NH₄⁺ to NH₃, the ammonia is distilled into a flask containing a known amount of HCl. The amount of unreacted HCl is determined by a back titration with standard strong base titrant. Because different cereal proteins contain similar amounts of nitrogen, multiplying the experimentally determined %w/w N by a factor of 5.7 gives the %w/w protein in the sample (on average there are 5.7 g protein for every gram of nitrogen).

Procedure

Transfer a 2.0-g sample of bread, which has previously been air-dried and ground into a powder, to a suitable digestion flask, along with 0.7 g of a HgO catalyst, 10 g of K₂SO₄, and 25 mL of concentrated H₂SO₄. Bring the solution to a boil. Continue boiling until the solution turns clear and then boil for at least an additional 30 minutes. After cooling the solution below room temperature, remove the Hg²⁺ catalyst by adding 200 mL of H₂O and 25 mL of 4% w/v K₂S. Add a few Zn granules to serve as boiling stones and 25 g of NaOH. Quickly connect the flask to a distillation apparatus and distill the NH₃ into a collecting flask containing a known amount of standardized HCl. The tip of the condenser must be placed below the surface of the strong acid. After the distillation is complete, titrate the excess strong acid with a standard solution of NaOH using methyl red as an indicator (Figure 9.18).

Questions

1. Oxidizing the protein converts all of its nitrogen to NH₄⁺. Why is the amount of nitrogen not determined by titrating the NH₄⁺ with a strong base?

There are two reasons for not directly titrating the ammonium ion. First, because NH₄⁺ is a very weak acid (its K_a is 5.6 × 10^–10), its titration with NaOH yields a poorly defined end point. Second, even if the end point can be determined with acceptable accuracy and precision, the solution also contains a substantial larger concentration of unreacted H₂SO₄. The presence of two acids that differ greatly in concentration makes for a difficult analysis. If the titrant’s concentration is similar to that of H₂SO₄, then the equivalence point volume for the titration of NH₄⁺ is too small to measure reliably. On the other hand, if the titrant’s concentration is similar to that of NH₄⁺, the volume needed to neutralize the H₂SO₄ is unreasonably large.

2. Ammonia is a volatile compound as evidenced by the strong smell of even dilute solutions. This volatility is a potential source of determinate error. Is this determinate error negative or positive?

Any loss of NH₃ is loss of nitrogen and, therefore, a loss of protein. The result is a negative determinate error.

3. Discuss the steps in this procedure that minimize this determinate error.

Three specific steps minimize the loss of ammonia: (1) the solution is cooled below room temperature before adding NaOH; (2) after adding NaOH, the digestion flask is quickly connected to the distillation apparatus; and (3) the condenser’s tip is placed below the surface of the HCl to ensure that the NH₃ reacts with the HCl before it can be lost through volatilization.

4. How does K₂S remove Hg²⁺, and why is its removal important?

Adding sulfide precipitates Hg²⁺ as HgS. This is important because NH₃ forms stable complexes with many metal ions, including Hg²⁺. Any NH₃ that reacts with Hg²⁺ is not collected during distillation, providing another source of determinate error.

Figure 9.18 Methyl red’s endpoint for the titration of a strong acid with a strong base; the indicator is: (a) red prior to the end point; (b) orange at the end point; and (c) yellow after the end point.

9.2.4 Q Quantitative Applications

Although many quantitative applications of acid–base titrimetry have been replaced by other analytical methods, a few important applications continue to be relevant. In this section we review the general application of acid–base titrimetry to the analysis of inorganic and organic compounds, with an emphasis on applications in environmental and clinical analysis. First, however, we discuss the selection and standardization of acidic and basic titrants.

Selecting and Standardizing a Titrant

The most common strong acid titrants are HCl, HClO₄, and H₂SO₄. Solutions of these titrants are usually prepared by diluting a commercially available concentrated stock solution. Because the concentrations of concentrated acids are known only approximately, the titrant’s concentration is determined by standardizing against one of the primary standard weak bases listed in Table 9.5.

Note

The nominal concentrations of the concentrated stock solutions are 12.1 M HCl, 11.7 M HClO₄, and 18.0 M H₂SO₄.

Table 9.5 Selected Primary Standards for Standardizing Strong Acid and Strong Base Titrants

Primary Standard	Standardization of Acidic Titrants Titration Reaction	Comment
Na2CO3	Na2CO3 + 2H3O^+ → H2CO3 + 2Na^+ + 2H2O	a
(HOCH2)3CNH2	(HOCH2)3CNH2 + H3O^+ → (HOCH2)3CNH3^+ + H2O	b
Na2B4O7	Na2B4O7 + 2H3O^+ + 3H2O → 2Na^+ + 4H3BO3
Primary Standard	Standardization of Basic Titrants Titration Reaction	Comment
KHC8H4O4	KHC8H4O4 + OH^− → K^+ + C8H4O4^− + H2O	c
C6H5COOH	C6H5COOH + OH^− → C6H5COO^− + H2O	d
KH(IO3)2	KH(IO3)2 + OH^− → K^+ + 2IO3^− + H2O

^a The end point for this titration is improved by titrating to the second equivalence point, boiling the solution to expel CO₂, and retitrating to the second equivalence point. The reaction in this case is
Na₂CO₃ + 2H₃O⁺ → CO₂ + 2Na⁺ + 3K^+
b Tris-(hydroxymethyl)aminomethane often goes by the shorter name of TRIS or THAM.
^c Potassium hydrogen phthalate often goes by the shorter name of KHP.
^d Because it is not very soluble in water, dissolve benzoic acid in a small amount of ethanol before diluting with water.

The most common strong base titrant is NaOH. Sodium hydroxide is available both as an impure solid and as an approximately 50% w/v solution. Solutions of NaOH may be standardized against any of the primary weak acid standards listed in Table 9.5.

Using NaOH as a titrant is complicated by potential contamination from the following reaction between CO₂ and OH^–.

\[\mathrm{CO_2}(aq)+2\mathrm{OH^-}(aq)\rightarrow \mathrm{CO_3^{2-}}(aq)+\mathrm{H_2O}(l)\tag{9.7}\]

Note

Any solution in contact with the atmosphere contains a small amount of CO₂(aq) from the equilibrium

\[\mathrm{CO_2}(g)\rightleftharpoons \mathrm{CO_2}(aq)\]

During the titration, NaOH reacts with both the titrand and CO₂, increasing the volume of NaOH needed to reach the titration’s end point. This is not a problem if end point pH is less than 6. Below this pH the CO₃^2– from reaction 9.7 reacts with H₃O⁺ to form carbonic acid.

\[\mathrm{CO_3^{2-}}(aq) + 2\mathrm{H_3O^+}(aq)\rightarrow \mathrm{H_2CO_3}(aq) + 2\mathrm{H_2O}(l)\tag{9.8}\]

Combining reaction 9.7 and reaction 9.8 gives an overall reaction that does not include OH^–.

\[\mathrm{CO_2}(aq)+\mathrm{H_2O}(l)\rightarrow \mathrm{H_2CO_3}(aq)\]

Under these conditions the presence of CO₂ does not affect the quantity of OH^– used in the titration and is not a source of determinate error.

If the end point pH is between 6 and 10, however, the neutralization of CO₃^2– requires one proton

\[\mathrm{CO_3^{2-}}(aq)+\mathrm{H_3O^+}(aq)\rightarrow \ce{HCO_3^-}(aq) + \mathrm{H_2O}(l)\]

and the net reaction between CO₂ and OH^– is

\[\mathrm{CO_2}(aq)+\mathrm{OH^-}(aq)\rightarrow \ce{HCO_3^-}(aq)\]

Under these conditions some OH^– is consumed in neutralizing CO₂, resulting in a determinate error. We can avoid the determinate error if we use the same end point pH in both the standardization of NaOH and the analysis of our analyte, although this often is not practical.

Solid NaOH is always contaminated with carbonate due to its contact with the atmosphere, and can not be used to prepare a carbonate-free solution of NaOH. Solutions of carbonate-free NaOH can be prepared from 50% w/v NaOH because Na₂CO₃ is insoluble in concentrated NaOH. When CO₂ is absorbed, Na₂CO₃ precipitates and settles to the bottom of the container, allowing access to the carbonate-free NaOH. When preparing a solution of NaOH, be sure to use water that is free from dissolved CO₂. Briefly boiling the water expels CO₂, and after cooling, it may be used to prepare carbonate-free solutions of NaOH. A solution of carbonate-free NaOH is relatively stable f we limit its contact with the atmosphere. Standard solutions of sodium hydroxide should not be stored in glass bottles as NaOH reacts with glass to form silicate; instead, store such solutions in polyethylene bottles.

Inorganic Analysis

Acid–base titrimetry is a standard method for the quantitative analysis of many inorganic acids and bases. A standard solution of NaOH can be used to determine the concentration of inorganic acids, such as H₃PO₄ or H₃AsO₄, and inorganic bases, such as Na₂CO₃ can be analyzed using a standard solution of HCl.

An inorganic acid or base that is too weak to be analyzed by an aqueous acid–base titration can be analyzed by adjusting the solvent, or by an indirect analysis. For example, when analyzing boric acid, H₃BO₃, by titrating with NaOH, accuracy is limited by boric acid’s small acid dissociation constant of 5.8 × 10^–10. (Figure 9.16a shows a typical result for the titration of H₃BO₃ with NaOH.) Boric acid’s K_a value increases to 1.5 × 10^–4 in the presence of mannitol, because it forms a complex with the borate ion. The result is a sharper end point and a more accurate titration. Similarly, the analysis of ammonium salts is limited by the small acid dissociation constant of 5.7 × 10^–10 for NH₄⁺. In this case, we can convert NH₄⁺ to NH₃ by neutralizing with strong base. The NH₃, for which K_b is 1.58 × 10^–5, is then removed by distillation and titrated with HCl.

We can analyze a neutral inorganic analyte if we can first convert it into an acid or base. For example, we can determine the concentration of NO₃^– by reducing it to NH₃ in a strongly alkaline solution using Devarda’s alloy, a mixture of 50% w/w Cu, 45% w/w Al, and 5% w/w Zn.

\[3\ce{NO_3^-}(aq)+8\mathrm{Al}(s)+5\mathrm{OH^-}(aq)+2\mathrm{H_2O}(l)\rightarrow 8\ce{AlO_2^-}(aq)+3\mathrm{NH_3}(aq)\]

The NH₃ is removed by distillation and titrated with HCl. Alternatively, we can titrate NO₃^– as a weak base by placing it in an acidic nonaqueous solvent such as anhydrous acetic acid and using HClO₄ as a titrant.

Acid–base titrimetry continues to be listed as a standard method for the determination of alkalinity, acidity, and free CO₂ in waters and wastewaters. Alkalinity is a measure of a sample’s capacity to neutralize acids. The most important sources of alkalinity are OH^–, HCO₃^–, and CO₃^2–, although other weak bases, such as phosphate, may contribute to the overall alkalinity. Total alkalinity is determined by titrating to a fixed end point pH of 4.5 (or to the bromocresol green end point) using a standard solution of HCl or H₂SO₄. Results are reported as mg CaCO₃/L.

Note

Although a variety of strong bases and weak bases may contribute to a sample’s alkalinity, a single titration cannot distinguish between the possible sources. Reporting the total alkalinity as if CaCO₃ is the only source provides a means for comparing the acid-neutralizing capacities of different samples.

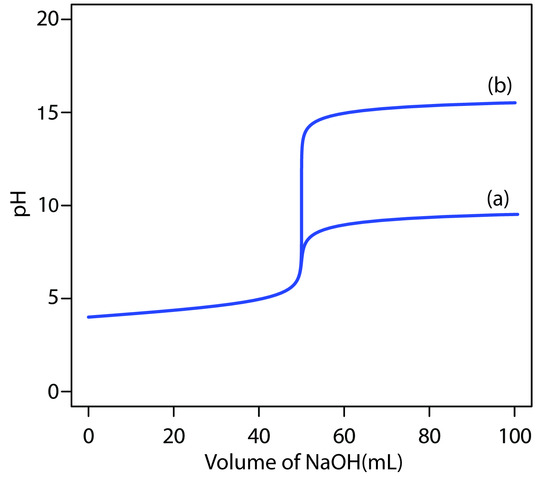
When the sources of alkalinity are limited to OH^–, HCO₃^–, and CO₃^2–, separate titrations to a pH of 4.5 (or the bromocresol green end point) and a pH of 8.3 (or the phenolphthalein end point) allow us to determine which species are present and their respective concentrations. Titration curves for OH^–, HCO₃^–, and CO₃^2– are shown in Figure 9.19. For a solution containing only OH^– alkalinity, the volumes of strong acid needed to reach the two end points are identical (Figure 9.19a). When the only source of alkalinity is CO₃^2–, the volume of strong acid needed to reach the end point at a pH of 4.5 is exactly twice that needed to reach the end point at a pH of 8.3 (Figure 9.19b). If a solution contains only HCO₃^– alkalinity, the volume of strong acid needed to reach the end point at a pH of 8.3 is zero, but that for the pH 4.5 end point is greater than zero (Figure 9.19c).

Figure 9.19 Titration curves for 50.0 mL of (a) 0.10 M NaOH, (b) 0.050 M Na₂CO₃, and (c) 0.10 M NaHCO₃ using 0.10 M HCl. The dashed lines indicate the fixed pH end points of 8.3 and 4.5. The color gradients show the phenolphthalein (red → colorless) and bromocresol green (blue → green) endpoints. When titrating to the phenolphthalein endpoint, the titration continues until the last trace of red is lost.

Mixtures of OH^– and CO₃^2–, or of HCO₃^– and CO₃^2– also are possible. Consider, for example, a mixture of OH^– and CO₃^2–. The volume of strong acid to titrate OH^– is the same whether we titrate to a pH of 8.3 or a pH of 4.5. Titrating CO₃^2– to a pH of 4.5, however, requires twice as much strong acid as titrating to a pH of 8.3. Consequently, when titrating a mixture of these two ions, the volume of strong acid to reach a pH of 4.5 is less than twice that to reach a pH of 8.3. For a mixture of HCO₃^– and CO₃^2– the volume of strong acid to reach a pH of 4.5 is more than twice that to reach a pH of 8.3. Table 9.6 summarizes the relationship between the sources of alkalinity and the volumes of titrant needed to reach the two end points.

Table 9.6 Relationship Between End Point Volumes and Sources of Alkalinity

Source of Alkalinity	Relationship Between End Point Volumes
OH^–	VpH 4.5 = VpH 8.3
CO3^2–	VpH 4.5 = 2×VpH 8.3
HCO3^–	VpH 4.5 > 0; VpH 8.3 = 0
OH^– and CO3^2–	VpH 4.5 < 2×VpH 8.3
CO3^2– and HCO3^–	VpH 4.5 > 2×VpH 8.3

Acidity is a measure of a water sample’s capacity for neutralizing base, and is conveniently divided into strong acid and weak acid acidity. Strong acid acidity, from inorganic acids such as HCl, HNO₃, and H₂SO₄, is common in industrial effluents and acid mine drainage. Weak acid acidity is usually dominated by the formation of H₂CO₃ from dissolved CO₂, but also includes contributions from hydrolyzable metal ions such as Fe³⁺, Al³⁺, and Mn²⁺. In addition, weak acid acidity may include a contribution from organic acids.

Acidity is determined by titrating with a standard solution of NaOH to fixed pH of 3.7 (or the bromothymol blue end point) and a fixed pH 8.3 (or the phenolphthalein end point). Titrating to a pH of 3.7 provides a measure of strong acid acidity, and titrating to a pH of 8.3 provides a measure of total acidity. Weak acid acidity is the difference between the total and strong acid acidities. Results are expressed as the amount of CaCO₃ that can be neutralized by the sample’s acidity. (As is the case with alkalinity, acidity is reported as mg CaCO₃/L.) An alternative approach for determining strong acid and weak acid acidity is to obtain a potentiometric titration curve and use a Gran plot to determine the two equivalence points. This approach has been used, for example, to determine the forms of acidity in atmospheric aerosols.⁴

Water in contact with either the atmosphere, or with carbonate-bearing sediments contains free CO₂ that exists in equilibrium with CO₂(g) and aqueous H₂CO₃, HCO₃^–, and CO₃^2–. (Free CO₂ is the same thing as CO₂(aq).) The concentration of free CO₂ is determined by titrating with a standard solution of NaOH to the phenolphthalein end point, or to a pH of 8.3, with results reported as mg CO₂/L. This analysis is essentially the same as that for the determination of total acidity, and can only be applied to water samples that do not contain strong acid acidity.

Organic Analysis

Acid–base titrimetry continues to have a small, but important role for the analysis of organic compounds in pharmaceutical, biochemical, agricultural, and environmental laboratories. Perhaps the most widely employed acid–base titration is the Kjeldahl analysis for organic nitrogen. Examples of analytes determined by a Kjeldahl analysis include caffeine and saccharin in pharmaceutical products, proteins in foods, and the analysis of nitrogen in fertilizers, sludges, and sediments. Any nitrogen present in a –3 oxidation state is quantitatively oxidized to NH₄⁺. Because some aromatic heterocyclic compounds, such as pyridine, are difficult to oxidize, a catalyst is used to ensure a quantitative oxidation. Nitrogen in other oxidation states, such as nitro and azo nitrogens, may be oxidized to N₂, resulting in a negative determinate error. Including a reducing agent, such as salicylic acid, converts this nitrogen to a –3 oxidation state, eliminating this source of error. Table 9.7 provides additional examples in which an element is quantitative converted into a titratable acid or base.

Note

See Representative Method 9.1 for one application of a Kjeldahl analysis.

Table 9.7 Selected Elemental Analyses Based on an Acid–Base Titration

Element	Convert to...	Reaction Producing Titratable Acid or Base^a	Titration Details
N	NH3(g)	NH3(g) + HCl(aq) → NH4^+(aq) + Cl^−(aq)	add HCl in excess and back titrate with NaOH
S	SO2(g)	SO2(g) + H2O2(aq) → H2SO4(aq)	titrate H2SO4 with NaOH
C	CO2(g)	CO2(g) + Ba(OH)2(aq) → BaCO3(s) + H2O(l)	add excess Ba(OH)2 and back titrate with HCl
Cl	HCl(g)	—	titrate HCl with NaOH
F	SiF4(g)	3SiF4(aq) + 2H2O(l) → 2H2SiF6(aq) + SiO2(s)	titrate H2SiF4 with NaOH

^a The species that is titrated is shown in bold.

Several organic functional groups are weak acids or weak bases. Carboxylic (–COOH), sulfonic (–SO₃H) and phenolic (–C₆H₅OH) functional groups are weak acids that can be successfully titrated in either aqueous or nonaqueous solvents. Sodium hydroxide is the titrant of choice for aqueous solutions. Nonaqueous titrations are often carried out in a basic solvent, such as ethylenediamine, using tetrabutylammonium hydroxide, (C₄H₉)₄NOH, as the titrant. Aliphatic and aromatic amines are weak bases that can be titrated using HCl in aqueous solution, or HClO₄ in glacial acetic acid. Other functional groups can be analyzed indirectly following a reaction that produces or consumes an acid or base. Typical examples are shown in Table 9.8.

Table 9.8 Selected Acid–Base Titrimetric Procedures for Organic Functional Groups Based on the Production or Consumption of Acid or Base

Functional Group	Reaction Producing Titratable Acid or Base^a	Titration Details
ester	RCOOR′(aq) + OH^−(aq) → RCOO^−(aq) + HOR′(aq)	titrate OH^– with HCl
carbonyl	R2C=O(aq) + NH2OHiHCl(aq) → R2C=NOH(aq) + HCl(aq) + H2O(l)	titrate HCl with NaOH
alcohol^b	[1] (CH3CO)2O + ROH → CH3COOR + CH3COOH [2] (CH3CO)2O + H2O → 2CH3COOH	titrate CH3COOH with NaOH; a blank titration of acetic anhydride,(CH3CO)2O, corrects for the contribution of reaction [2]

^a The species that is titrated is shown in bold.
^b The acetylation reaction [1] is carried out in pyridine to prevent the hydrolysis of acetic by water. After the acetylation reaction is complete, water is added to covert any unreacted acetic anhydride to acetic acid [2].

Many pharmaceutical compounds are weak acids or bases that can be analyzed by an aqueous or nonaqueous acid–base titration; examples include salicylic acid, phenobarbital, caffeine, and sulfanilamide. Amino acids and proteins can be analyzed in glacial acetic acid using HClO₄ as the titrant. For example, a procedure for determining the amount of nutritionally available protein uses an acid–base titration of lysine residues.⁵

Quantitative Calculations

The quantitative relationship between the titrand and the titrant is determined by the stoichiometry of the titration reaction. If the titrand is polyprotic, then we must know to which equivalence point we are titrating. The following example illustrates how we can use a ladder diagram to determine a titration reaction’s stoichiometry.

Example 9.2

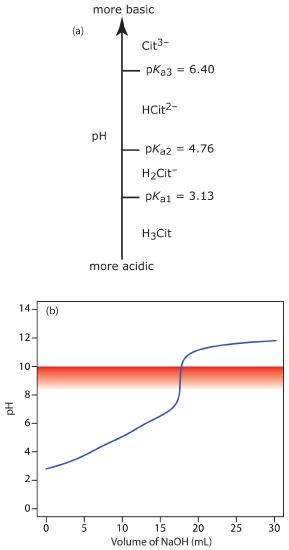
A 50.00 mL sample of a citrus drink requires 17.62 mL of 0.04166 M NaOH to reach the phenolphthalein end point. Express the sample’s acidity as grams of citric acid, C₆H₈O₇, per 100 mL.

Solution

Because citric acid is a triprotic weak acid, we must first determine if the phenolphthalein end point corresponds to the first, second, or third equivalence point. Citric acid’s ladder diagram is shown in Figure 9.20a. Based on this ladder diagram, the first equivalence point is between a pH of 3.13 and a pH of 4.76, the second equivalence point is between a pH of 4.76 and a pH of 6.40, and the third equivalence point is greater than a pH of 6.40. Because phenolphthalein’s end point pH is 8.3–10.0 (see Table 9.4), the titration proceeds to the third equivalence point and the titration reaction is

\[\mathrm{C_6H_8O_7}(aq)+3\mathrm{OH^-}(aq)\rightarrow \mathrm{C_6H_5O_7}^{3-}(aq)+3\mathrm{H_2O}(l)\]

In reaching the equivalence point, each mole of citric acid consumes three moles of NaOH; thus

\[0.04166\textrm{ M NaOH} \times 0.01762\textrm{ L NaOH} = 7.3405\times10^{-5}\textrm{ moles NaOH}\]

\[7.3405\times10^{-5}\textrm{ mol NaOH}\times\dfrac{\mathrm{1\;mol\;C_6H_8O_7}}{\mathrm{3\;mol\;NaOH}}= 2.4468\times10^{-4}\mathrm{\;mol\;C_6H_8O_7}\]

\[2.4468\times10^{-4}\textrm{ mol }\mathrm{C_6H_8O_7}\times\dfrac{192.13\textrm{ g }\mathrm{C_6H_8O_7}}{\textrm{mol }\mathrm{C_6H_8O_7}}= 0.04701\textrm{ g } \mathrm{C_6H_8O_7}\]

Because this is the amount of citric acid in a 50.00 mL sample, the concentration of citric acid in the citrus drink is 0.09402 g/100 mL. The complete titration curve is shown in Figure 9.20b.

Figure 9.20 (a) Ladder diagram for citric acid; (b) Titration curve for the sample in Example 9.2 showing phenolphthalein’s pH transition region.

Practice Exercise 9.6

Your company recently received a shipment of salicylic acid, C₇H₆O₃, to be used in the production of acetylsalicylic acid (aspirin). The shipment can be accepted only if the salicylic acid is more than 99% pure. To evaluate the shipment’s purity, a 0.4208-g sample is dissolved in water and titrated to the phenolphthalein end point, requiring 21.92 mL of 0.1354 M NaOH. Report the shipment’s purity as %w/w C₇H₆O₃. Salicylic acid is a diprotic weak acid with pK_a values of 2.97 and 13.74.

Click here to review your answer to this exercise.

In an indirect analysis the analyte participates in one or more preliminary reactions, one of which produces or consumes acid or base. Despite the additional complexity, the calculations are straightforward.

Example 9.3

The purity of a pharmaceutical preparation of sulfanilamide, C₆H₄N₂O₂S, is determined by oxidizing sulfur to SO₂ and bubbling it through H₂O₂ to produce H₂SO₄. The acid is titrated to the bromothymol blue end point with a standard solution of NaOH. Calculate the purity of the preparation given that a 0.5136-g sample requires 48.13 mL of 0.1251 M NaOH.

Solution

The bromothymol blue end point has a pH range of 6.0–7.6. Sulfuric acid is a diprotic acid, with a pK_a2 of 1.99 (the first K_a value is very large and the acid dissociation reaction goes to completion, which is why H₂SO₄ is a strong acid). The titration, therefore, proceeds to the second equivalence point and the titration reaction is

\[\mathrm{H_2SO_4}(aq)+\mathrm{2OH^-}(aq)\rightarrow \mathrm{2H_2O}(l)+\mathrm{SO_4^{2-}}(aq)\]

Using the titration results, there are

\[0.1251\textrm{ M NaOH}\times0.04813\textrm{ L NaOH}= 6.021\times10^{-3}\textrm{ mol NaOH}\]

\[6.021\times10^{-3}\textrm{ mol NaOH} \times \dfrac{1\textrm{ mol }\mathrm{H_2SO_4}}{2\textrm{ mol NaOH}}= 3.010\times10^{-3}\textrm{ mol }\mathrm{H_2SO_4}\]

produced by bubbling SO₂ through H₂O₂. Because all the sulfur in H₂SO₄ comes from the sulfanilamide, we can use a conservation of mass to determine the amount of sulfanilamide in the sample.

\[3.010\times10^{-3}\textrm{ mol }\mathrm{H_2SO_4}\times\dfrac{\textrm{1 mol S}}{\textrm{ mol }\mathrm{H_2SO_4}}\times\dfrac{\textrm{1 mol }\mathrm{C_6H_4N_2O_2S}}{\textrm{mol S}}\times\dfrac{168.18\textrm{ g }\mathrm{C_6H_4N_2O_2S}}{\textrm{mol }\mathrm{C_6H_4N_2O_2S}}\]

\[=0.5062\textrm{ g }\mathrm{C_6H_4N_2O_2S}\]

\[\dfrac{0.5062\textrm{ g }\mathrm{C_6H_4N_2O_2S}}{0.5136\textrm{ g sample}}\times100 = 98.56\%\textrm{ w/w }\mathrm{C_6H_4N_2O_2S}\]

Practice Exercise 9.7

The concentration of NO₂ in air can be determined by passing the sample through a solution of H₂O₂, which oxidizes NO₂ to HNO₃, and titrating the HNO₃ with NaOH. What is the concentration of NO₂, in mg/L, if a 5.0 L sample of air requires 9.14 mL of 0.01012 M NaOH to reach the methyl red end point

Click here to review your answer to this exercise.

Example 9.4

The amount of protein in a sample of cheese is determined by a Kjeldahl analysis for nitrogen. After digesting a 0.9814-g sample of cheese, the nitrogen is oxidized to NH₄⁺, converted to NH₃ with NaOH, and distilled into a collection flask containing 50.00 mL of 0.1047 M HCl. The excess HCl is back titrated with 0.1183 M NaOH, requiring 22.84 mL to reach the bromothymol blue end point. Report the %w/w protein in the cheese assuming that there are 6.38 grams of protein for every gram of nitrogen in most dairy products.

(For a back titration we must consider two acid–base reactions. Again, the calculations are straightforward.)

Solution

The HCl in the collection flask reacts with two bases

\[\textrm{HCl}(aq)+\mathrm{NH_3}(aq)\rightarrow \mathrm{NH_4^+}(aq)+\mathrm{Cl^-}(aq)\]

\[\mathrm{HCl}(aq)+\mathrm{OH^-}(aq)\rightarrow \mathrm{H_2O}(l)+\mathrm{Cl^-}(aq)\]

The collection flask originally contains

\[0.1047\textrm{ M HCl} \times 0.05000\textrm{ L HCl} = 5.235\times10^{-3}\textrm{ mol HCl}\]

of which

\[\textrm{0.1183 M NaOH}\times\textrm{0.02284 L NaOH} \times\dfrac{\textrm{1 mol HCl}}{\textrm{mol NaOH}}= 2.702\times10^{-3}\textrm{ mol HCl}\]

react with NaOH. The difference between the total moles of HCl and the moles of HCl reacting with NaOH

\[5.235\times10^{-3}\textrm{ mol HCl}-2.702\times10^{-3}\textrm{ mol HCl}=2.533\times10^{-3}\textrm{ mol HCl}\]

is the moles of HCl reacting with NH₃. Because all the nitrogen in NH₃ comes from the sample of cheese, we use a conservation of mass to determine the grams of nitrogen in the sample.

\[2.533\times10^{-3}\textrm{ mol HCl}\times\dfrac{\textrm{1 mol }\mathrm{NH_3}}{\textrm{mol HCl}}\times\dfrac{\textrm{14.01 g N}}{\textrm{mol }\mathrm{NH_3}}=\textrm{0.03549 g N}\]

The mass of protein, therefore, is

\[\textrm{0.03549 g N} \times\dfrac{\textrm{6.38 g protein}}{\textrm{g N}}=\textrm{0.2264 g protein}\]

and the % w/w protein is

\[\dfrac{\textrm{0.2264 g protein}}{\textrm{0.9814 g sample}}\times100=\textrm{23.1% w/w protein}\]

Practice Exercise 9.8

Limestone consists mainly of CaCO₃, with traces of iron oxides and other metal oxides. To determine the purity of a limestone, a 0.5413-g sample is dissolved using 10.00 mL of 1.396 M HCl. After heating to expel CO₂, the excess HCl was titrated to the phenolphthalein end point, requiring 39.96 mL of 0.1004 M NaOH. Report the sample’s purity as %w/w CaCO₃.

Click here to review your answer to this exercise.

Earlier we noted that we can use an acid–base titration to analyze a mixture of acids or bases by titrating to more than one equivalence point. The concentration of each analyte is determined by accounting for its contribution to each equivalence point.

Example 9.5

The alkalinity of natural waters is usually controlled by OH^–, HCO₃^–, and CO₃^2–, which may be present singularly or in combination. Titrating a 100.0-mL sample to a pH of 8.3 requires 18.67 mL of a 0.02812 M HCl. A second 100.0-mL aliquot requires 48.12 mL of the same titrant to reach a pH of 4.5. Identify the sources of alkalinity and their concentrations in milligrams per liter.

Solution

Because the volume of titrant to reach a pH of 4.5 is more than twice that needed to reach a pH of 8.3, we know, from Table 9.6, that the sample’s alkalinity is controlled by CO₃^2– and HCO₃^–. Titrating to a pH of 8.3 neutralizes CO₃^2– to HCO₃^–

\[\mathrm{CO_3^{2-}}(aq)+\textrm{HCl}(aq)\rightarrow \ce{HCO_3^-}(aq)+\mathrm{Cl^-}(aq)\]

but there is no reaction between the titrant and HCO₃^– (see Figure 9.19). The concentration of CO₃^2– in the sample, therefore, is

\[\textrm{0.02812 M HCl} \times \textrm{0.01867 L HCl} \times\dfrac{\textrm{1 mol CO}_3^{2-}}{\textrm{mol HCl}}= 5.250\times10^{-4}\textrm{ mol }\mathrm{CO_3^{2-}}\]

\[\dfrac{5.250\times10^{-4}\textrm{ mol }\mathrm{CO_3^{2-}}}{\textrm{0.1000 L}} \times\dfrac{60.01\textrm{ g }\mathrm{CO_3^{2-}}}{\textrm{mol }\mathrm{CO_3^{2-}}}\times\dfrac{\textrm{1000 mg}}{\textrm g}=\textrm{315.1 mg/L}\]

Titrating to a pH of 4.5 neutralizes CO₃²⁻ to H₂CO₃, and HCO₃^– to H₂CO₃ (see Figures 9.19).

\[\mathrm{CO_3^{2-}}(aq)+\textrm{2HCl}(aq)\rightarrow \mathrm{H_2CO_3}(aq)+\mathrm{2Cl^-}(aq)\]

\[\ce{HCO_3^-}(aq)+\mathrm{HCl}(aq)\rightarrow \mathrm{H_2CO_3}(aq)+\mathrm{2Cl^-}(aq)\]

Because we know how many moles of CO₃^2– are in the sample, we can calculate the volume of HCl it consumes.

\[5.250\times10^{-4}\mathrm{\;mol\;CO_3^{2-}} \times\dfrac{\textrm{2 mol HCl}}{\mathrm{mol\;CO_3^{2-}}}\times\dfrac{\textrm{1 L HCl}}{\textrm{0.02812 mol HCl}}\times\dfrac{\textrm{1000 mL}}{\textrm L}=37.34\textrm{ mL}\]

This leaves 48.12 mL - 37.34 mL, or 10.78 mL of HCl to react with HCO₃^–. The amount of HCO₃^– in the sample is

\[\textrm{0.02812 M HCl}\times\textrm{0.01078 L HCl}\times\dfrac{\ce{1\;mol\;HCO_3^-}}{\textrm{mol HCl}}=3.031\times10^{-4}\mathrm{\;mol\;\ce{HCO_3^-}}\]

\[\dfrac{3.031\times10^{-4}\mathrm{\;mol\;\ce{HCO_3^-}}}{0.1000\textrm{ L}}\times\dfrac{\mathrm{61.02\;g\;\ce{HCO_3^-}}}{\mathrm{mol\;\ce{HCO_3^-}}}\times\dfrac{\textrm{1000 mg}}{\textrm g}=\textrm{185.0 mg/L}\]

Practice Exercise 9.9

Samples containing the monoprotic weak acids 2–methylanilinium chloride (C₇H₁₀NCl, pK_a = 4.447) and 3–nitrophenol (C₆H₅NO₃, pK_a = 8.39) can be analyzed by titrating with NaOH. A 2.006-g sample requires 19.65 mL of 0.200 M NaOH to reach the bromocresol purple end point and 48.41 mL of 0.200 M NaOH to reach the phenolphthalein end point. Report the %w/w of each compound in the sample.

Click here to review your answer to this exercise.

9.2.5 Qualitative Applications

Example 9.5 shows how we can use an acid–base titration to assign the forms of alkalinity in waters. We can easily extend this approach to other systems. For example, by titrating with either a strong acid or a strong base to the methyl orange and phenolphthalein end points we can determine the composition of solutions containing one or two of the following species: H₃PO₄, H₂PO₄^–, HPO₄^2–, PO₄^3–, HCl, and NaOH. As outlined in Table 9.9, each species or mixture of species has a unique relationship between the volumes of titrant needed to reach these two end points.

Table 9.9 Relationship Between End Point Volumes for Mixtures of Phosphate Species with HCl and NaOH

Solution Composition	Relationship Between End Point Volumes with Strong Base Titrant^a	Relationship Between End Point Volumes With Strong Acid Titrant^a
H3PO4	VPH = 2 × VMO	—^b
H2PO4^–	VPH > 0; VMO = 0	—
HPO4^2–	—	VMO > 0; VPH = 0
PO4^3–	—	VMO = 2 × VPH
HCl	VPH = VMO	—
NaOH	—	VMO = VPH
HCl and H3PO4	VPH < 2 × VMO	—
H3PO4 and H2PO4^–	VPH > 2 × VMO	—
H2PO4^– and HPO4^2–	VPH > 0; VMO = 0	VMO > 0; VPH = 0
HPO4^2– and PO4^3–	—	VMO > 2 × VPH
PO4^3– and NaOH	—	VMO < 2 × VPH

^a V_PH and V_MO are, respectively, the volume of titrant at the phenolphthalein and methyl orange end points.
^b When no information is provided, the volume of titrant to each end point is zero.

9.2.6 Characterization Applications

An acid–base titration can be use to characterize the chemical and physical properties of matter. Two useful characterization applications are the determination of a compound’s equivalent weight and its acid or its base dissociation constant.

Equivalent Weights

Suppose we titrate a sample containing an impure weak acid to a well-defined end point using a monoprotic strong base as the titrant. If we assume that the titration involves the transfer of n protons, then the moles of titrant needed to reach the end point is

\[\textrm{moles titrant}=\dfrac{n\textrm{ moles titrant}}{\textrm{moles analyte}}\times{\textrm{moles analyte}}\]

If we know the analyte’s identity, we can use this equation to determine the amount of analyte in the sample

\[\textrm{grams analyte} = \textrm{moles titrant}\times\dfrac{\textrm{1 mole analyte}}{n\textrm{ moles titrant}}\times\textrm{FW analyte}\]

where FW is the analyte’s formula weight.

But what if we do not know the analyte’s identify? If we can titrate a pure sample of the analyte, we can obtain some useful information that may help in establishing its identity. Because we do not know the number of protons being titrated, we let n = 1 and replace the analyte’s formula weight with its equivalent weight (EW)

\[\textrm{grams analyte} = \textrm{moles titrant}\times\dfrac{\textrm{1 equivalent analyte}}{\textrm{1 moles titrant}}\times\textrm{EW analyte}\]

where

\[\textrm{FW}=n\times\textrm{EW}\]

Example 9.6

A 0.2521-g sample of an unknown weak acid is titrated with 0.1005 M NaOH, requiring 42.68 mL to reach the phenolphthalein end point. Determine the compound’s equivalent weight. Which of the following compounds is most likely to be the unknown weak acid?

ascorbic acid	C8H8O6	FW = 176.1	monoprotic
malonic acid	C3H4O4	FW = 104.1	diprotic
succinic acid	C4H6O4	FW = 118.1	diprotic
citric acid	C6H8O7	FW = 192.1	triprotic

Solution

The moles of NaOH needed to reach the end point is

\[\textrm{0.1005 M NaOH} \times \textrm{0.04268 L NaOH} = 4.289\times10^{-3}\textrm{ mol NaOH}\]

which gives the analyte’s equivalent weight as

\[EW=\dfrac{\textrm{g analyte}}{\textrm{equiv. analyte}}=\dfrac{\textrm{0.2521 g}}{4.289\times10^{-3}\textrm{ equiv.}}=\textrm{58.78 g/equivalent}\]

The possible formula weights for the weak acid are

\[n = 1:\hspace{2 mm} \textrm{FW = EW = 58.78 g/equivalent}\]

\[n = 2: \hspace{2 mm} \mathrm{FW = 2\times EW = 117.6\;g/equivalent}\]

\[n = 3: \hspace{2 mm} \mathrm{FW = 3\times EW = 176.3\;g/equivalent}\]

If the analyte is a monoprotic weak acid, then its formula weight is 58.78 g/mol, eliminating ascorbic acid as a possibility. If it is a diprotic weak acid, then the analyte’s formula weight is either 58.78 g/mol or 117.6 g/mol, depending on whether the titration is to the first or second equivalence point. Succinic acid, with a formula weight of 118.1 g/mole is a possibility, but malonic acid is not. If the analyte is a triprotic weak acid, then its formula weight is 58.78 g/mol, 117.6 g/mol, or 176.3 g/mol. None of these values is close to the formula weight for citric acid, eliminating it as a possibility. Only succinic acid provides a possible match.

Practice Exercise 9.10

Figure 9.21 shows the potentiometric titration curve for the titration of a 0.500-g sample an unknown weak acid. The titrant is 0.1032 M NaOH. What is the weak acid’s equivalent weight?

Click here to review your answer to this exercise.

Figure 9.21 Titration curve for Practice Exercise 9.10.

Equilibrium Constants

Another application of acid–base titrimetry is the determination of equilibrium constants. Consider, for example, a solution of acetic acid, CH₃COOH, for which the dissociation constant is

\[K_\textrm a=\dfrac{[\mathrm{H_3O^+}][\mathrm{CH_3COO^-}]}{[\mathrm{CH_3COOH]}}\]

When the concentrations of CH₃COOH and CH₃COO^– are equal, the K_a expression reduces to K_a = [H₃O⁺], or pH = pK_a. If we titrate a solution of acetic acid with NaOH, the pH equals the pK_a when the volume of NaOH is approximately ½V_eq. As shown in Figure 9.22, a potentiometric titration curve provides a reasonable estimate of acetic acid’s pK_a.

Figure 9.22 Estimating acetic acid’s pK_a using its potentiometric titration curve.

This method provides a reasonable estimate of a weak acid’s pK_a if the acid is neither too strong nor too weak. These limitations are easily to appreciate if we consider two limiting cases. For the first case let’s assume that the weak acid, HA, is more than 50% dissociated before the titration begins (a relatively large K_a value). The concentration of HA before the equivalence point is always less than the concentration of A^–, and there is no point on the titration curve where [HA] = [A⁻]. At the other extreme, if the acid is too weak, less than 50% of the weak acid reacts with the titrant at the equivalence point. In this case the concentration of HA before the equivalence point is always greater than that of A^–. Determining the pK_a by the half-equivalence point method overestimates its value if the acid is too strong and underestimates its value if the acid is too weak.

Practice Exercise 9.11

Use the potentiometric titration curve in Figure 9.21 to estimate the pK_a values for the weak acid in Practice Exercise 9.10.

Click here to review your answer to this exercise.

A second approach for determining a weak acid’s pK_a is to use a Gran plot. For example, earlier in this chapter we derived the following equation for the titration of a weak acid with a strong base.

\[[\mathrm{H_3O^+}]\times V_\textrm b=K_\textrm aV_\textrm{eq}-K_\textrm aV_\textrm b\]

A plot of [H₃O⁺] × V_b versus V_b, for volumes less than the equivalence point, yields a straight line with a slope of –K_a. Other linearizations have been developed which use the entire titration curve, or that require no assumptions.⁶ This approach to determining acidity constants has been used to study the acid–base properties of humic acids, which are naturally occurring, large molecular weight organic acids with multiple acidic sites. In one study a humic acid was found to have six titratable sites, three of which were identified as carboxylic acids, two of which were believed to be secondary or tertiary amines, and one of which was identified as a phenolic group.⁷

9.2.7 Evaluation of Acid–Base Titrimetry

Scale of Operation

In an acid–base titration the volume of titrant needed to reach the equivalence point is proportional to the moles of titrand. Because the pH of the titrand or the titrant is a function of its concentration, however, the change in pH at the equivalence point—and thus the feasibility of an acid–base titration—depends on their respective concentrations. Figure 9.23, for example, shows a series of titration curves for the titration of several concentrations of HCl with equimolar solutions NaOH. For titrand and titrant concentrations smaller than 10^–3 M, the change in pH at the end point may be too small to provide accurate and precise results.

Note

Acid–base titrimetry is an example of a total analysis technique in which the signal is proportional to the absolute amount of analyte. See Chapter 3 for a discussion of the difference between total analysis techniques and concentration techniques.

Figure 9.23 Titration curves for 25.0 mL of (a) 10^–1 M HCl, (b) 10^–2 M HCl, (c) 10^–3 M HCl, (d) 10^–4 M HCl, and (e) 10^–5 M HCl. In each case the titrant is an equimolar solution of NaOH.

A minimum concentration of 10^–3 M places limits on the smallest amount of analyte that we can successfully analyze. For example, suppose our analyte has a formula weight of 120 g/mol. To successfully monitor the titration’s end point using an indicator or with a pH probe, the titrand needs an initial volume of approximately 25 mL. If we assume that the analyte’s formula weight is 120 g/mol, then each sample must contain at least 3 mg of analyte. For this reason, acid–base titrations are generally limited to major and minor analytes (see Figure 3.6 in Chapter 3). We can extend the analysis of gases to trace analytes by pulling a large volume of the gas through a suitable collection solution.

One goal of analytical chemistry is to extend analyses to smaller samples. Here we describe two interesting approaches to titrating μL and pL samples. In one experimental design (Figure 9.24), samples of 20–100 μL were held by capillary action between a flat-surface pH electrode and a stainless steel sample stage.⁸ The titrant was added by using the oscillations of a piezoelectric ceramic device to move an angled glass rod in and out of a tube connected to a reservoir containing the titrant. Each time the glass tube was withdrawn an approximately 2 nL microdroplet of titrant was released. The microdroplets were allowed to fall onto the sample, with mixing accomplished by spinning the sample stage at 120 rpm. A total of 450 microdroplets, with a combined volume of 0.81–0.84 μL, was dispensed between each pH measurement. In this fashion a titration curve was constructed. This method was used to titrate solutions of 0.1 M HCl and 0.1 M CH₃COOH with 0.1 M NaOH. Absolute errors ranged from a minimum of +0.1% to a maximum of –4.1%, with relative standard deviations from 0.15% to 4.7%. Sample as small as 20 μL were successfully titrated.

Figure 9.24 Experimental design for a microdroplet titration apparatus.

Another approach carries out the acid–base titration in a single drop of solution.⁹ The titrant is delivered using a microburet fashioned from a glass capillary micropipet (Figure 9.25). The microburet has a 1-2 μm tip filled with an agar gel membrane. The tip of the microburet is placed within a drop of the sample solution, which is suspended in heptane, and the titrant is allowed to diffuse into the sample. The titration’s progress is monitored using an acid–base indicator, and the time needed to reach the end point is measured. The rate of the titrant’s diffusion from the microburet is determined by a prior calibration. Once calibrated the end point time can be converted to an end point volume. Samples usually consisted of picoliter volumes (10^–12 liters), with the smallest sample being 0.7 pL. The precision of the titrations was usually about 2%.

Figure 9.25 Experimental set-up for a diffusional microtitration. The indicator is a mixture of bromothymol blue and bromocresol purple.

Titrations conducted with microliter or picoliter sample volumes require a smaller absolute amount of analyte. For example, diffusional titrations have been successfully conducted on as little as 29 femtomoles (10^–15 moles) of nitric acid. Nevertheless, the analyte must still be present in the sample at a major or minor level for the titration to be performed accurately and precisely.

Accuracy

When working with a macro–major or a macro–minor sample, an acid–base titration can achieve a relative error of 0.1–0.2%. The principal limitation to accuracy is the difference between the end point and the equivalence point.

Note

See Figure 3.5 in Chapter 3 to review the characteristics of macro–major and macro–minor samples.

Precision

An acid–base titration’s relative precision depends primarily on the precision with which we can measure the end point volume and the precision in detecting the end point. Under optimum conditions, an acid–base titration has a relative precision of 0.1–0.2%. We can improve the relative precision by using the largest possible buret and ensuring that we use most of its capacity in reaching the end point. A smaller volume buret is a better choice when using costly reagents, when waste disposal is a concern, or when the titration must be completed quickly to avoid competing chemical reactions. Automatic titrators are particularly useful for titrations requiring small volumes of titrant because they provide significantly better precision (typically about ±0.05% of the buret’s volume).

The precision of detecting the end point depends on how it is measured and the slope of the titration curve at the end point. With an indicator the precision of the end point signal is usually ±0.03–0.10 mL. Potentiometric end points usually are more precise.

Sensitivity

For an acid–base titration we can write the following general analytical equation relating the titrant’s volume to the absolute amount of titrand

\[\textrm{volume of titrant} = k \times \textrm{moles of titrand}\]

where k, the sensitivity, is determined by the stoichiometry between the titrand and the titrant. Consider, for example, the determination of sulfurous acid, H₂SO₃, by titrating with NaOH to the first equivalence point

\[\mathrm{H_2SO_3}(aq)+\mathrm{OH^-}(aq)\rightarrow \mathrm{H_2O}(l)+\ce{HSO_3^-}(aq)\]

At the equivalence point the relationship between the moles of NaOH and the moles of H₂SO₃ is

\[\textrm{mol NaOH = mol }\mathrm{H_2SO_3}\]

Substituting the titrant’s molarity and volume for the moles of NaOH and rearranging

\[M_\textrm{NaOH} \times V_\textrm{NaOH} =\textrm{ mol }\mathrm{H_2SO_3}\]

\[V_\textrm{NaOH}=\dfrac{1}{M_\textrm{NaOH}}\times\mathrm{mol\;H_2SO_3}\]

we find that k is

\[k=\dfrac{1}{M_\textrm{NaOH}}\]

There are two ways in which we can improve a titration’s sensitivity. The first, and most obvious, is to decrease the titrant’s concentration because it is inversely proportional to the sensitivity, k.

The second approach, which only applies if the titrand is multiprotic, is to titrate to a later equivalence point. If we titrate H₂SO₃ to the second equivalence point

\[\mathrm{H_2SO_3}(aq)+\mathrm{2OH^-}(aq)\rightarrow \mathrm{2H_2O}(l)+\mathrm{SO_3^{2-}}(aq)\]

then each mole of H₂SO₃ consumes two moles of NaOH

\[\textrm{mol NaOH}= 2 \times\mathrm{mol\;H_2SO_3}\]

and the sensitivity becomes

\[k=\dfrac{2}{M_\textrm{NaOH}}\]

In practice, however, any improvement in sensitivity is offset by a decrease in the end point’s precision if the larger volume of titrant requires us to refill the buret. Consequently, standard acid–base titrimetric procedures are written to ensure that titrations require 60–100% of the buret’s volume.

Selectivity

Acid–base titrants are not selective. A strong base titrant, for example, reacts with all acids in a sample, regardless of their individual strengths. If the titrand contains an analyte and an interferent, then selectivity depends on their relative acid strengths. Two limiting situations must be considered.

If the analyte is a stronger acid than the interferent, then the titrant will react with the analyte before it begins reacting with the interferent. The feasibility of the analysis depends on whether the titrant’s reaction with the interferent affects the accurate location of the analyte’s equivalence point. If the acid dissociation constants are substantially different, the end point for the analyte can be accurately determined. Conversely, if the acid dissociation constants for the analyte and interferent are similar, then an accurate end point for the analyte may not be found. In the latter case a quantitative analysis for the analyte is not possible.

In the second limiting situation the analyte is a weaker acid than the interferent. In this case the volume of titrant needed to reach the analyte’s equivalence point is determined by the concentration of both the analyte and the interferent. To account for the interferent’s contribution to the end point, an end point for the interferent must be present. Again, if the acid dissociation constants for the analyte and interferent are significantly different, then the analyte’s determination is possible. If the acid dissociation constants are similar, however, there is only a single equivalence point and the analyte’s and interferent’s contributions to the equivalence point volume can not be separated.

Time, Cost, and Equipment

Acid–base titrations require less time than most gravimetric procedures, but more time than many instrumental methods of analysis, particularly when analyzing many samples. With an automatic titrator, however, concerns about analysis time are less significant. When performing a titration manually our equipment needs—a buret and, perhaps, a pH meter—are few in number, inexpensive, routinely available, and easy to maintain. Automatic titrators are available for between $3000 and $10 000.

Contributors

David Harvey (DePauw University)