9.3: Complexation Titrations

The earliest examples of metal–ligand complexation titrations are Liebig’s determinations, in the 1850s, of cyanide and chloride using, respectively, Ag⁺ and Hg²⁺ as the titrant. Practical analytical applications of complexation titrimetry were slow to develop because many metals and ligands form a series of metal–ligand complexes. Liebig’s titration of CN^– with Ag⁺ was successful because they form a single, stable complex of Ag(CN)₂^–, giving a single, easily identified end point. Other metal–ligand complexes, such as CdI₄^2–, are not analytically useful because they form a series of metal–ligand complexes (CdI⁺, CdI₂(aq), CdI₃^– and CdI₄^2–) that produce a sequence of poorly defined end points.

Note

Recall that an acid–base titration curve for a diprotic weak acid has a single end point if its two K_a values are not sufficiently different. See Figure 9.11 for an example.

In 1945, Schwarzenbach introduced aminocarboxylic acids as multidentate ligands. The most widely used of these new ligands—ethylenediaminetetraacetic acid, or EDTA—forms strong 1:1 complexes with many metal ions. The availability of a ligand that gives a single, easily identified end point made complexation titrimetry a practical analytical method.

9.3.1 Chemistry and Properties of EDTA

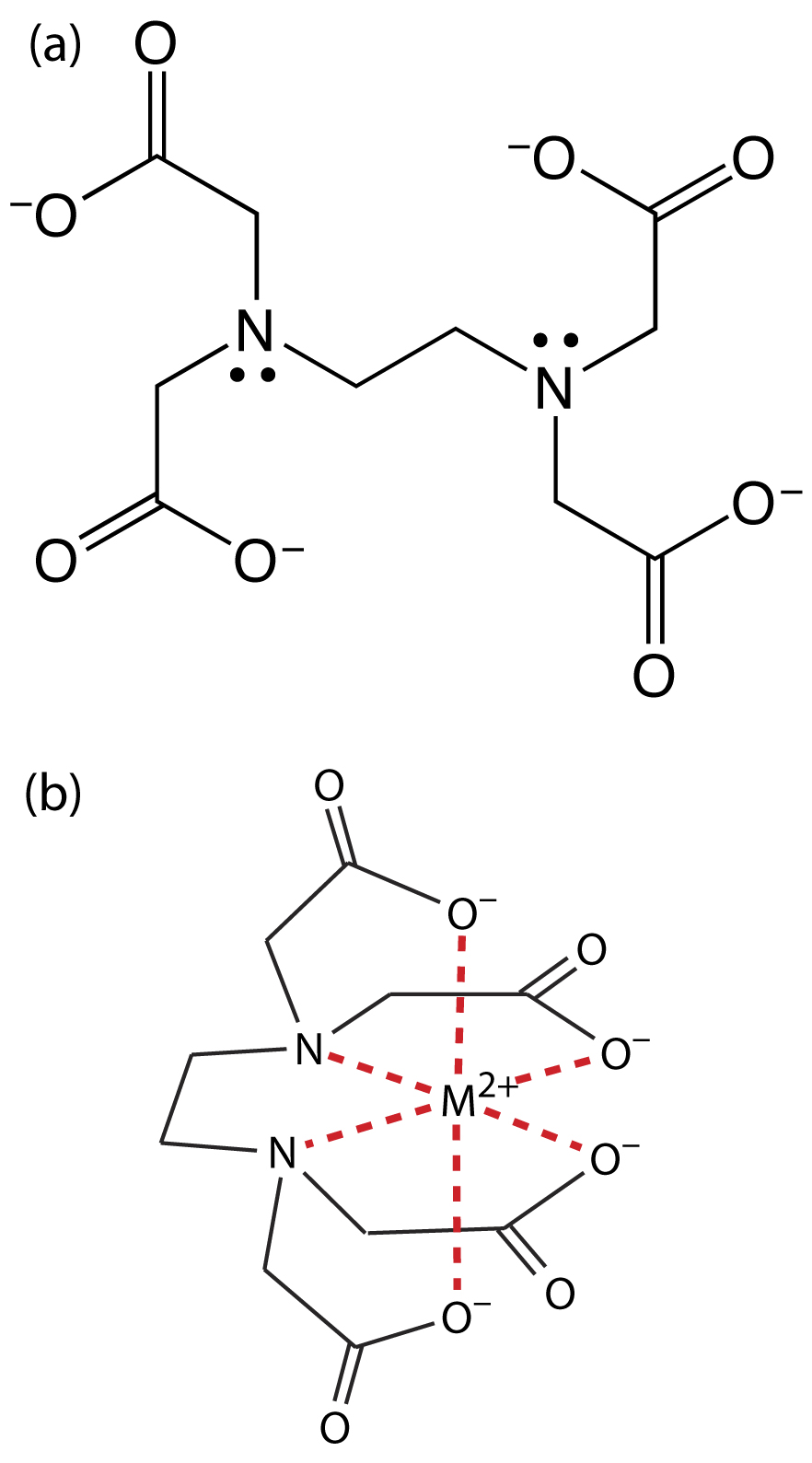
Ethylenediaminetetraacetic acid, or EDTA, is an aminocarboxylic acid. EDTA, which is shown in Figure 9.26a in its fully deprotonated form, is a Lewis acid with six binding sites—four negatively charged carboxylate groups and two tertiary amino groups—that can donate six pairs of electrons to a metal ion. The resulting metal–ligand complex, in which EDTA forms a cage-like structure around the metal ion (Figure 9.26b), is very stable. The actual number of coordination sites depends on the size of the metal ion, however, all metal–EDTA complexes have a 1:1 stoichiometry.

Figure 9.26 Structures of (a) EDTA, in its fully deprotonated form, and (b) in a six-coordinate metal–EDTA complex with a divalent metal ion.

Metal–ED TA Formation Constants

To illustrate the formation of a metal–EDTA complex, let’s consider the reaction between Cd²⁺ and EDTA

\[\mathrm{Cd^{2+}}(aq)+\mathrm{Y^{4-}}(aq)\rightleftharpoons \mathrm{CdY^{2-}}(aq)\tag{9.9}\]

where Y^4– is a shorthand notation for the fully deprotonated form of EDTA shown in Figure 9.26a. Because the reaction’s formation constant

\[K_\textrm f=\dfrac{[\textrm{CdY}^{2-}]}{[\textrm{Cd}^{2+}][\textrm{Y}^{4-}]}=2.9\times10^{16}\tag{9.10}\]

is large, its equilibrium position lies far to the right. Formation constants for other metal–EDTA complexes are found in Table E4.

EDTA is a Weak Acid

In addition to its properties as a ligand, EDTA is also a weak acid. The fully protonated form of EDTA, H₆Y²⁺, is a hexaprotic weak acid with successive pK_a values of

\(\textrm pK_{\textrm a1} = 0.0\) \(\textrm pK_{\textrm a4} = 2.66\)

\(\textrm pK_{\textrm a2} = 1.5\) \(\textrm pK_{\textrm a5} = 6.16\)

\(\textrm pK_{\textrm a3} = 2.0\) \(\textrm pK_{\textrm a6} = 10.24\)

The first four values are for the carboxylic acid protons and the last two values are for the ammonium protons. Figure 9.27 shows a ladder diagram for EDTA. The specific form of EDTA in reaction 9.9 is the predominate species only at pH levels greater than 10.17.

Figure 9.27 Ladder diagram for EDTA.

Conditional Metal–Ligand Formation Constants

The formation constant for CdY^2– in equation 9.10 assumes that EDTA is present as Y^4–. Because EDTA has many forms, when we prepare a solution of EDTA we know it total concentration, C_EDTA, not the concentration of a specific form, such as Y^4–. To use equation 9.10, we need to rewrite it in terms of C_EDTA.

At any pH a mass balance on EDTA requires that its total concentration equal the combined concentrations of each of its forms.

\[C_\textrm{EDTA}=[\mathrm{H_6Y^{2+}}]+[\mathrm{H_5Y^+}]+[\mathrm{H_4Y}]+[\mathrm{H_3Y^-}]+[\mathrm{H_2Y^{2-}}]+[\mathrm{HY^{3-}}]+[\mathrm{Y^{4-}}]\]

To correct the formation constant for EDTA’s acid–base properties we need to calculate the fraction, α_Y^4–, of EDTA present as Y^4–.

\[\alpha_{\textrm Y^{4-}} \dfrac{[\textrm Y^{4-}]}{C_\textrm{EDTA}}\tag{9.11}\]

Table 9.10 Values of α_Y^4- for Selected pH Levels

pH	αY^4–	pH	αY^4–
1	1.9×10^–18	8	5.6×10^–3
2	3.4×10^–14	9	5.4×10^–2
3	2.6×10^–11	10	0.37
4	3.8×10^–9	11	0.85
5	3.7×10^–7	12	0.98
6	2.4×10^–5	13	1.00
7	5.0×10^–4	14	1.00

Note

Problem 9.42 from the end of chapter problems asks you to verify the values in Table 9.10 by deriving an equation for α_Y^4-.

Table 9.10 provides values of α_Y^4– for selected pH levels. Solving equation 9.11 for [Y⁴⁻] and substituting into equation 9.10 for the CdY^2– formation constant

\[K_\textrm f =\dfrac{[\textrm{CdY}^{2-}]}{[\textrm{Cd}^{2+}]\alpha_{\textrm Y^{4-}}C_\textrm{EDTA}}\]

and rearranging gives

\[K_f'=K_f\times \alpha_{\textrm Y^{4-}}=\dfrac{[\mathrm{CdY^{2-}}]}{[\mathrm{Cd^{2+}}]C_\textrm{EDTA}}\tag{9.12}\]

where K_f´ is a pH-dependent conditional formation constant. As shown in Table 9.11, the conditional formation constant for CdY^2– becomes smaller and the complex becomes less stable at more acidic pHs.

Table 9.11 Conditional Formation Constants for CdY^2-

pH	Kf´	pH	Kf´
1	5.5 × 10^–2	8	1.6 × 10^14
2	1.0 × 10^3	9	1.6 × 10^15
3	7.7 × 10^5	10	1.1× 10^16
4	1.1 × 10^8	11	2.5 × 10^16
5	1.1 × 10^10	12	2.9 × 10^16
6	6.8 × 10^11	13	2.9 × 10^16
7	1.5 × 10^13	14	2.9 × 10^16

EDTA Competes With Other Ligands

To maintain a constant pH during a complexation titration we usually add a buffering agent. If one of the buffer’s components is a ligand that binds Cd²⁺, then EDTA must compete with the ligand for Cd²⁺. For example, an NH₄⁺/NH₃ buffer includes NH₃, which forms several stable Cd²⁺–NH₃ complexes. Because EDTA forms a stronger complex with Cd²⁺ it will displace NH₃, but the stability of the Cd²⁺–EDTA complex decreases.

We can account for the effect of an auxiliary complexing agent, such as NH₃, in the same way we accounted for the effect of pH. Before adding EDTA, the mass balance on Cd²⁺, C_Cd, is

\[C_\textrm{Cd}=[\mathrm{Cd^{2+}}]+[\mathrm{Cd(NH_3)^{2+}}]+[\mathrm{Cd(NH_3)_2^{2+}}]+[\mathrm{Cd(NH_3)_3^{2+}}]+[\mathrm{Cd(NH_3)_4^{2+}}]\]

and the fraction of uncomplexed Cd²⁺, α_Cd²⁺, is

\[\alpha_{\textrm{Cd}^{2+}}=\dfrac{[\mathrm{Cd^{2+}}]}{C_\textrm{Cd}}\tag{9.13}\]

Note

The value of α_Cd²⁺ depends on the concentration of NH₃. Contrast this with α_Y^4-, which depends on pH.

Solving equation 9.13 for [Cd²⁺] and substituting into equation 9.12 gives

\[K_\textrm f' =K_\textrm f \times \alpha_{\textrm Y^{4-}} = \dfrac{[\mathrm{CdY^{2-}}]}{\alpha_\mathrm{Cd^{2+}}C_\textrm{Cd}C_\textrm{EDTA}}\]

Because the concentration of NH₃ in a buffer is essentially constant, we can rewrite this equation

\[K_\textrm f''=K_\textrm f\times\alpha_\mathrm{Y^{4-}}\times\alpha_\mathrm{Cd^{2+}}=\dfrac{[\mathrm{CdY^{2-}}]}{C_\textrm{Cd}C_\textrm{EDTA}}\tag{9.14}\]

to give a conditional formation constant, K_f´´, that accounts for both pH and the auxiliary complexing agent’s concentration. Table 9.12 provides values of α_M²⁺ for several metal ion when NH₃ is the complexing agent.

Table 9.12 Values of α_M²⁺ for Selected Concentrations of Ammonia

[NH3](M)	αCa^2^+	αCd^2^+	αCo^2^+	αCu^2^+	αMg^2^+	αNi^2^+	αZn^2^+
1	5.50×10^–1	6.09×10^–8	1.00×10^–6	3.79×10^–14	1.76×10^–1	9.20×10^–10	3.95×10^–10
0.5	7.36×10^–1	1.05×10^–6	2.22×10^–5	6.86×10^–13	4.13×10^–1	3.44×10^–8	6.27×10^–9
0.1	9.39×10^–1	3.51×10^–4	6.64×10^–3	4.63×10^–10	8.48×10^–1	5.12×10^–5	3.68×10^–6
0.05	9.69×10^–1	2.72×10^–3	3.54×10^–2	7.17×10^–9	9.22×10^–1	6.37×10^–4	5.45×10^–5
0.01	9.94×10^–1	8.81×10^–2	3.55×10^–1	3.22×10^–6	9.84×10^–1	4.32×10^–2	1.82×10^–2
0.005	9.97×10^–1	2.27×10^–1	5.68×10^–1	3.62×10^–5	9.92×10^–1	1.36×10^–1	1.27×10^–1
0.001	9.99×10^–1	6.09×10^–1	8.84×10^–1	4.15×10^–3	9.98×10^–1	5.76×10^–1	7.48×10^–1

9.3.2 Complexometric EDTA Titration Curves

Now that we know something about EDTA’s chemical properties, we are ready to evaluate its usefulness as a titrant. To do so we need to know the shape of a complexometric EDTA titration curve. In section 9B we learned that an acid–base titration curve shows how the titrand’s pH changes as we add titrant. The analogous result for a complexation titration shows the change in pM, where M is the metal ion, as a function of the volume of EDTA. In this section we will learn how to calculate a titration curve using the equilibrium calculations from Chapter 6. We also will learn how to quickly sketch a good approximation of any complexation titration curve using a limited number of simple calculations.

Calculating the Titration Curve

Let’s calculate the titration curve for 50.0 mL of 5.00 × 10^–3 M Cd²⁺ using a titrant of 0.0100 M EDTA. Furthermore, let’s assume that the titrand is buffered to a pH of 10 with a buffer that is 0.0100 M in NH₃.

Note

Step 1: Calculate the conditional formation constant for the metal–EDTA complex.

Because the pH is 10, some of the EDTA is present in forms other than Y^4–. In addition, EDTA must compete with NH₃ for the Cd²⁺. To evaluate the titration curve, therefore, we first need to calculate the conditional formation constant for CdY^2–. From Table 9.10 and Table 9.11 we find that α_Y^4– is 0.35 at a pH of 10, and that α_Cd²⁺ is 0.0881 when the concentration of NH₃ is 0.0100 M. Using these values, the conditional formation constant is

\[K_\textrm f''=K_\textrm f \times \alpha_\mathrm{Y^{4-}}\times\alpha_\mathrm{Cd^{2+}}=(2.9\times10^{16})(0.37)(0.0881)=9.5\times10^{14}\]

Because K_f´´ is so large, we can treat the titration reaction

\[\textrm{Cd}^{2+}(aq)+\textrm Y^{4-}(aq)\rightarrow \textrm{CdY}^{2-}(aq)\]

as if it proceeds to completion.

Note

Step 2: Calculate the volume of EDTA needed to reach the equivalence point.

The next task in calculating the titration curve is to determine the volume of EDTA needed to reach the equivalence point. At the equivalence point we know that

\[\textrm{moles EDTA = moles Cd}^{2+}\]

\[M_\textrm{EDTA}\times V_\textrm{EDTA}=M_\textrm{Cd}\times V_\textrm{Cd}\]

Substituting in known values, we find that it requires

\[V_\textrm{eq}=V_\textrm{EDTA}=\dfrac{M_\textrm{Cd}V_\textrm{Cd}}{M_\textrm{EDTA}}=\dfrac{(5.00\times10^{-3}\;\textrm M)(\textrm{50.0 mL})}{\textrm{0.0100 M}}=\textrm{25.0 mL}\]

of EDTA to reach the equivalence point.

Note

Step 3: Calculate pM values before the equivalence point by determining the concentration of unreacted metal ions.

Before the equivalence point, Cd²⁺ is present in excess and pCd is determined by the concentration of unreacted Cd²⁺. Because not all the unreacted Cd²⁺ is free—some is complexed with NH₃—we must account for the presence of NH₃. For example, after adding 5.0 mL of EDTA, the total concentration of Cd²⁺ is

\[\begin{align}
C_\textrm{Cd}&=\dfrac{\textrm{initial moles Cd}^{2+} - \textrm{moles EDTA added}}{\textrm{total volume}}=\dfrac{M_\textrm{Cd}V_\textrm{Cd}-M_\textrm{EDTA}V_\textrm{EDTA}}{V_\textrm{Cd}+V_\textrm{EDTA}}\\
&=\dfrac{(5.00\times10^{-3}\textrm{ M})(\textrm{50.0 mL}) - (\textrm{0.0100 M})(\textrm{5.0 mL})}{\textrm{50.0 mL + 5.0 mL}}=3.64\times10^{-3}\textrm{ M}
\end{align}\]

To calculate the concentration of free Cd²⁺ we use equation 9.13

\[[\mathrm{Cd^{2+}}] = \alpha_\mathrm{Cd^{2+}} \times C_\textrm{Cd} = (0.0881)(3.64\times10^{-4}\textrm{ M})=3.21\times10^{-4}\textrm{ M}\]

which gives a pCd of

\[\textrm{pCd}=-\log[\mathrm{Cd^{2+}}]=-\log(3.21\times10^{-4}) = 3.49\]

Note

Step 4: Calculate pM at the equivalence point using the conditional formation constant.

At the equivalence point all the Cd²⁺ initially in the titrand is now present as CdY^2–. The concentration of Cd²⁺, therefore, is determined by the dissociation of the CdY^2– complex. First, we calculate the concentration of CdY^2–.

\[\begin{align}
[\mathrm{CdY^{2-}}]&=\dfrac{\textrm{initial moles Cd}^{2+}}{\textrm{total volume}}=\dfrac{M_\textrm{Cd}V_\textrm{Cd}}{V_\textrm{Cd}+V_\textrm{EDTA}}\\
&=\dfrac{(5.00\times10^{-3}\textrm{ M})(\textrm{50.0 mL})}{\textrm{50.0 mL + 25.0 mL}}=3.33\times10^{-3}\textrm{ M}
\end{align}\]

Next, we solve for the concentration of Cd²⁺ in equilibrium with CdY^2–.

\[K_\textrm f''=\dfrac{[\mathrm{CdY^{2-}}]}{C_\textrm{Cd}C_\textrm{EDTA}}=\dfrac{3.33\times10^{-3}-x}{(x)(x)}= 9.5\times10^{14}\]

\[x=C_\textrm{Cd}=1.9\times10^{-9}\textrm{ M}\]

Note

At the equivalence point the initial moles of Cd²⁺ and the moles of EDTA added are equal. The total concentrations of Cd²⁺, C_Cd, and the total concentration of EDTA, C_EDTA, are equal.

Once again, to find the concentration of uncomplexed Cd²⁺ we must account for the presence of NH₃; thus

\[[\mathrm{Cd^{2+}}]=\alpha_\mathrm{Cd^{2+}}\times C_\textrm{Cd}=(0.0881)(1.9\times10^{-9}\textrm{ M}) = 1.70\times10^{-10}\textrm{ M}\]

and pCd is 9.77 at the equivalence point.

Note

Step 5: Calculate pM after the equivalence point using the conditional formation constant.

After the equivalence point, EDTA is in excess and the concentration of Cd²⁺ is determined by the dissociation of the CdY^2– complex. First, we calculate the concentrations of CdY^2– and of unreacted EDTA. For example, after adding 30.0 mL of EDTA

\[\begin{align}
[\mathrm{CdY^{2-}}]&=\dfrac{\textrm{initial moles Cd}^{2+}}{\textrm{total volume}}=\dfrac{M_\textrm{Cd}V_\textrm{Cd}}{V_\textrm{Cd}+V_\textrm{EDTA}}\\
&=\dfrac{(5.00\times10^{-3}\textrm{ M})(\textrm{50.0 mL})}{\textrm{50.0 mL + 30.0 mL}}=3.13\times10^{-3}\textrm{ M}
\end{align}\]

\[\begin{align}
C_\textrm{EDTA}&=\dfrac{M_\textrm{EDTA}V_\textrm{EDTA}-M_\textrm{Cd}V_\textrm{Cd}}{V_\textrm{Cd}+V_\textrm{EDTA}}\\
&=\dfrac{\textrm{(0.0100 M)(30.0 mL)} - (5.00\times10^{-3}\textrm{ M})(\textrm{50.0 mL})}{\textrm{50.0 mL + 30.0 mL}}\\
&=6.25\times10^{-4}\textrm{ M}
\end{align}\]

Substituting into equation 9.14 and solving for [Cd²⁺] gives

\[\dfrac{[\mathrm{CdY^{2-}}]}{C_\textrm{Cd}C_\textrm{EDTA}} = \dfrac{3.13\times10^{-3}\textrm{ M}}{C_\textrm{Cd}(6.25\times10^{-4}\textrm{ M})} = 9.5\times10^{14}\]

\[C_\textrm{Cd}=5.4\times10^{-15}\textrm{ M}\]

\[[\mathrm{Cd^{2+}}] = \alpha_\mathrm{Cd^{2+}} \times C_\textrm{Cd} = (0.0881)(5.4\times10^{-15}\textrm{ M}) = 4.8\times10^{-16}\textrm{ M}\]

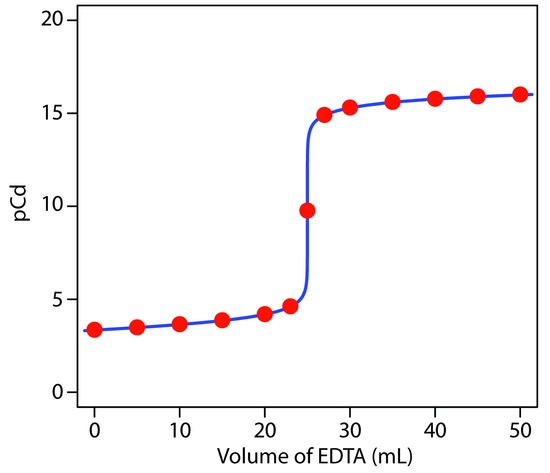
a pCd of 15.32. Table 9.13 and Figure 9.28 show additional results for this titration.

Note

After the equilibrium point we know the equilibrium concentrations of CdY^2- and EDTA. We can solve for the equilibrium concentration of C_Cd using K_f´´ and then calculate [Cd²⁺] using α_Cd²⁺. Because we use the same conditional formation constant, K_f´´, for all calculations, this is the approach shown here.

There is a second method for calculating [Cd²⁺] after the equivalence point. Because the calculation uses only [CdY²⁻] and C_EDTA, we can use K_f´ instead of K_f´´; thus

\[\dfrac{[\mathrm{CdY^{2-}}]}{[\mathrm{Cd^{2+}}]C_\textrm{EDTA}}=\alpha_\mathrm{Y^{4-}}\times K_\textrm f\]

\[\dfrac{3.13\times10^{-3}\textrm{ M}}{[\mathrm{Cd^{2+}}](6.25\times10^{-4}\textrm{ M})} = (0.37)(2.9\times10^{16})\]

Solving gives [Cd²⁺] = 4.7×10^–16 M and a pCd of 15.33. We will use this approach when learning how to sketch a complexometric titration curve.

Table 9.13 Titration of 50.0 mL of 5.00x10^-3 M Cd²⁺ with 0.0100 M EDTA at a pH of 10 and in the Presence of 0.0100 M NH₃

Volume of EDTA (mL)	pCd	Volume of EDTA (mL)	pCd
0.00	3.36	27.0	14.95
5.00	3.49	30.0	15.33
10.0	3.66	35.0	15.61
15.0	3.87	40.0	15.76
20.0	4.20	45.0	15.86
23.0	4.62	50.0	15.94

Figure 9.28 Titration curve for the titration of 50.0 mL of 5.00×10^–3 M Cd²⁺ with 0.0100 M EDTA at a pH of 10 and in the presence of 0.0100 M NH₃. The red points correspond to the data in Table 9.13. The blue line shows the complete titration curve.

Practice Exercise 9.12

Calculate titration curves for the titration of 50.0 mL of 5.00×10^–3 M Cd²⁺ with 0.0100 M EDTA (a) at a pH of 10 and (b) at a pH of 7. Neither titration includes an auxiliary complexing agent. Compare your results with Figure 9.28 and comment on the effect of pH and of NH₃ on the titration of Cd²⁺ with EDTA.

Click here to review your answer to this exercise.

Sketching an EDTA Titration Curve

To evaluate the relationship between a titration’s equivalence point and its end point, we need to construct only a reasonable approximation of the exact titration curve. In this section we demonstrate a simple method for sketching a complexation titration curve. Our goal is to sketch the titration curve quickly, using as few calculations as possible. Let’s use the titration of 50.0 mL of 5.00×10^–3 M Cd²⁺ with 0.0100 M EDTA in the presence of 0.0100 M NH₃ to illustrate our approach.

Note

This is the same example that we used in developing the calculations for a complexation titration curve. You can review the results of that calculation in Table 9.13 and Figure 9.28.

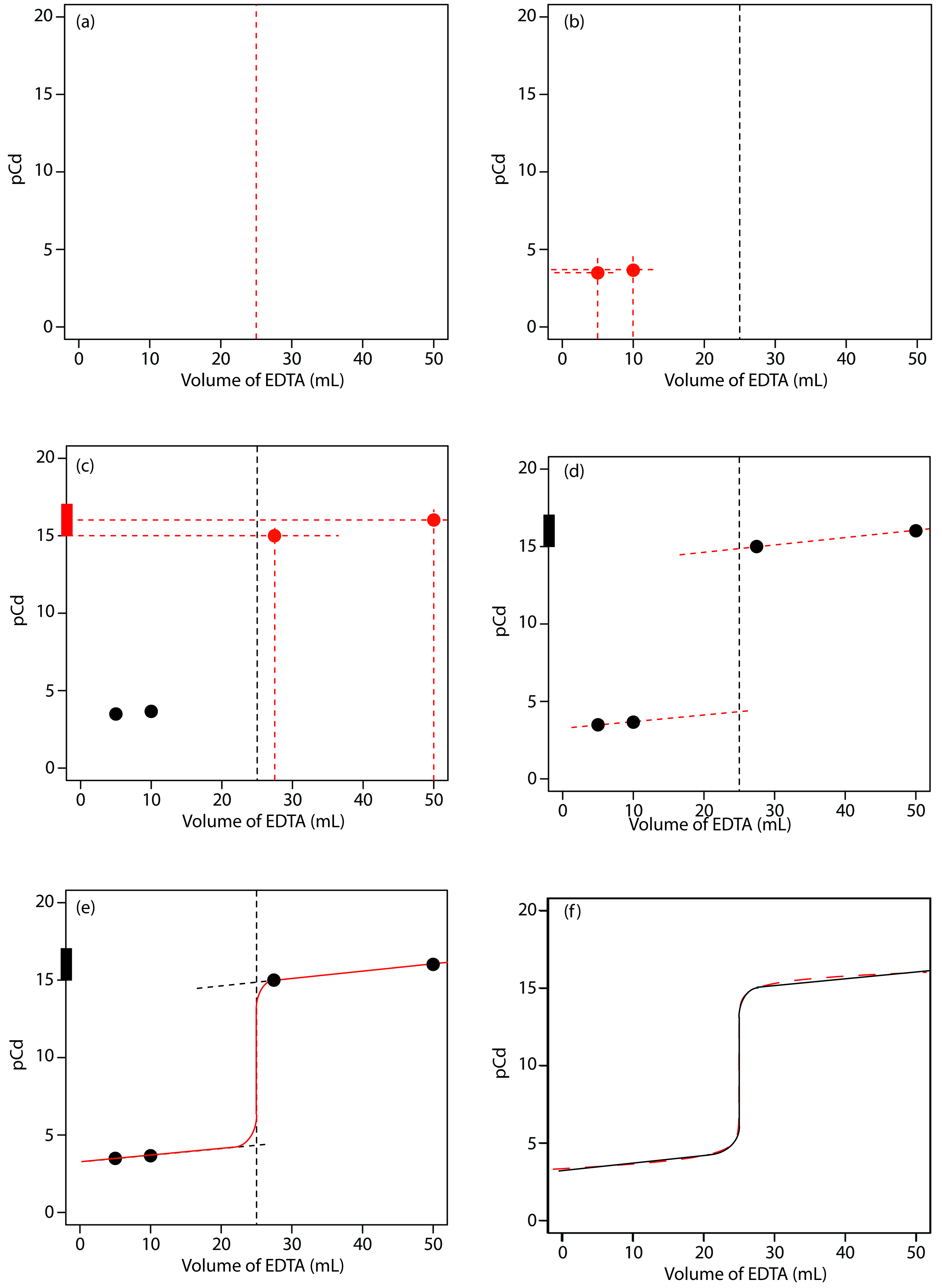
We begin by calculating the titration’s equivalence point volume, which, as we determined earlier, is 25.0 mL. Next, we draw our axes, placing pCd on the y-axis and the titrant’s volume on the x-axis. To indicate the equivalence point’s volume, we draw a vertical line corresponding to 25.0 mL of EDTA. Figure 9.29a shows the result of the first step in our sketch.

Before the equivalence point, Cd²⁺ is present in excess and pCd is determined by the concentration of unreacted Cd²⁺. Because not all the unreacted Cd²⁺ is free—some is complexed with NH₃—we must account for the presence of NH₃. The calculations are straightforward, as we saw earlier. Figure 9.29b shows the pCd after adding 5.00 mL and 10.0 mL of EDTA.

Note

See Table 9.13 for the values.

Figure 9.29 Illustrations showing the steps in sketching an approximate titration curve for the titration of 50.0 mL of 5.00 × 10^–3 M Cd²⁺ with 0.0100 M EDTA in the presence of 0.0100 M NH₃: (a) locating the equivalence point volume; (b) plotting two points before the equivalence point; (c) plotting two points after the equivalence point; (d) preliminary approximation of titration curve using straight-lines; (e) final approximation of titration curve using a smooth curve; (f) comparison of approximate titration curve (solid black line) and exact titration curve (dashed red line). See the text for additional details.

The third step in sketching our titration curve is to add two points after the equivalence point. Here the concentration of Cd²⁺ is controlled by the dissociation of the Cd²⁺–EDTA complex. Beginning with the conditional formation constant

\[K_\textrm f'=\dfrac{[\mathrm{CdY^{2-}}]}{[\mathrm{Cd^{2+}}]C_\textrm{EDTA}}=\alpha_\mathrm{Y^{4-}} \times K_\textrm f = (0.37)(2.9\times10^{16})=1.1\times10^{16}\]

we take the log of each side and rearrange, arriving at

\[\log K_\textrm f'=-\log[\mathrm{Cd^{2+}}]+\log\dfrac{[\mathrm{CdY^{2-}}]}{C_\textrm{EDTA}}\]

\[\textrm{pCd}=\log K_\textrm f'+\log\dfrac{C_\textrm{EDTA}}{[\mathrm{CdY^{2-}}]}\]

Note

See the final side comment in the previous section for an explanation of why we are ignoring the effect of NH₃ on the concentration of Cd²⁺.

Note that after the equivalence point, the titrand’s solution is a metal–ligand complexation buffer, with pCd determined by C_EDTA and [CdY^2–]. The buffer is at its lower limit of pCd = logK_f´ – 1 when

\[\dfrac{C_\textrm{EDTA}}{[\mathrm{CdY^{2-}}]}=\dfrac{\textrm{moles EDTA added} - \textrm{initial moles }\mathrm{Cd^{2+}}}{\textrm{initial moles }\mathrm{Cd^{2+}}}=\dfrac{1}{10}\]

Making appropriate substitutions and solving, we find that

\[\dfrac{M_\textrm{EDTA}V_\textrm{EDTA}-M_\textrm{Cd}V_\textrm{Cd}}{M_\textrm{Cd}V_\textrm{Cd}}=\dfrac{1}{10}\]

\[M_\textrm{EDTA}V_\textrm{EDTA}-M_\textrm{Cd}V_\textrm{Cd}=0.1 \times M_\textrm{Cd}V_\textrm{Cd}\]

\[V_\textrm{EDTA}=\dfrac{1.1 \times M_\textrm{Cd}V_\textrm{Cd}}{M_\textrm{EDTA}}=1.1\times V_\textrm{eq}\]

Thus, when the titration reaches 110% of the equivalence point volume, pCd is logK_f´ – 1. A similar calculation should convince you that pCd = logK_f´ when the volume of EDTA is 2×V_eq.

Note

Our derivation here is general and applies to any complexation titration using EDTA as a titrant.

Figure 9.29c shows the third step in our sketch. First, we add a ladder diagram for the CdY^2– complex, including its buffer range, using its logK_f´ value of 16.04. Next, we add points representing pCd at 110% of V_eq (a pCd of 15.04 at 27.5 mL) and at 200% of V_eq (a pCd of 16.04 at 50.0 mL).

Next, we draw a straight line through each pair of points, extending the line through the vertical line representing the equivalence point’s volume (Figure 9.29d). Finally, we complete our sketch by drawing a smooth curve that connects the three straight-line segments (Figure 9.29e). A comparison of our sketch to the exact titration curve (Figure 9.29f) shows that they are in close agreement.

Practice Exercise 9.13

Sketch titration curves for the titration of 50.0 mL of 5.00×10^–3 M Cd²⁺ with 0.0100 M EDTA (a) at a pH of 10 and (b) at a pH of 7. Compare your sketches to the calculated titration curves from Practice Exercise 9.12.

Click here to review your answer to this exercise.

9.3.3 Selecting and Evaluating the End point

The equivalence point of a complexation titration occurs when we react stoichiometrically equivalent amounts of titrand and titrant. As is the case with acid–base titrations, we estimate the equivalence point of a complexation titration using an experimental end point. A variety of methods are available for locating the end point, including indicators and sensors that respond to a change in the solution conditions.

Finding the End point with an Indicator

Most indicators for complexation titrations are organic dyes—known as metallochromic indicators—that form stable complexes with metal ions. The indicator, In^m–, is added to the titrand’s solution where it forms a stable complex with the metal ion, MIn^n–. As we add EDTA it reacts first with free metal ions, and then displaces the indicator from MIn^n–.

\[\textrm{MIn}^{n-}+\textrm Y^{4-}\rightarrow\textrm{MY}^{2-}+\textrm{In}^{m-}\]

If MIn^n– and In^m– have different colors, then the change in color signals the end point.

The accuracy of an indicator’s end point depends on the strength of the metal–indicator complex relative to that of the metal–EDTA complex. If the metal–indicator complex is too strong, the change in color occurs after the equivalence point. If the metal–indicator complex is too weak, however, the end point occurs before we reach the equivalence point.

Most metallochromic indicators also are weak acids. One consequence of this is that the conditional formation constant for the metal–indicator complex depends on the titrand’s pH. This provides some control over an indicator’s titration error because we can adjust the strength of a metal–indicator complex by adjusted the pH at which we carry out the titration. Unfortunately, because the indicator is a weak acid, the color of the uncomplexed indicator also changes with pH. Figure 9.30, for example, shows the color of the indicator calmagite as a function of pH and pMg, where H₂In^–, HIn^2–, and In^3– are different forms of the uncomplexed indicator, and MgIn^– is the Mg²⁺–calmagite complex. Because the color of calmagite’s metal–indicator complex is red, its use as a metallochromic indicator has a practical pH range of approximately 8.5–11 where the uncomplexed indicator, HIn^2–, has a blue color.

Note

Figure 9.30 is essentially a two-variable ladder diagram. The solid lines are equivalent to a step on a conventional ladder diagram, indicating conditions where two (or three) species are equal in concentration.

Figure 9.30 (a) Predominance diagram for the metallochromic indicator calmagite showing the most important form and color of calmagite as a function of pH and pMg, where H₂In^–, HIn^2–, and In^3– are uncomplexed forms of calmagite, and MgIn^– is its complex with Mg²⁺. Conditions to the right of the dashed line, where Mg²⁺ precipitates as Mg(OH)₂, are not analytically useful for a complexation titration. A red to blue end point is possible if we maintain the titrand’s pH in the range 8.5–11. (b) Diagram showing the relationship between the concentration of Mg²⁺ (as pMg) and the indicator’s color. The ladder diagram defines pMg values where MgIn^– and HIn^– are predominate species. The indicator changes color when pMg is between logK_f – 1 and logK_f + 1.

Table 9.14 provides examples of metallochromic indicators and the metal ions and pH conditions for which they are useful. Even if a suitable indicator does not exist, it is often possible to complete an EDTA titration by introducing a small amount of a secondary metal–EDTA complex, if the secondary metal ion forms a stronger complex with the indicator and a weaker complex with EDTA than the analyte. For example, calmagite gives poor end points when titrating Ca²⁺ with EDTA. Adding a small amount of Mg²⁺–EDTA to the titrand gives a sharper end point. Because Ca²⁺ forms a stronger complex with EDTA, it displaces Mg²⁺, which then forms the red-colored Mg²⁺–calmagite complex. At the titration’s end point, EDTA displaces Mg²⁺ from the Mg²⁺–calmagite complex, signaling the end point by the presence of the uncomplexed indicator’s blue form.

Table 9.14 Selected Metallochromic Indicators

Indicator	pH Range	Metal Ions^a
calmagite	8.5–11	Ba, Ca, Mg, Zn
eriochrome Black T	7.5–10.5	Ba, Ca, Mg, Zn
eriochrome Blue Black R	8–12	Ca, Mg, Zn, Cu
murexide	6–13	Ca, Ni, Cu
PAN	2–11	Cd, Cu, Zn
salicylic acid	2–3	Fe

^a metal ions in italic font have poor end points

Finding the End point by Monitoring Absorbance

Note

Two other methods for finding the end point of a complexation titration are a thermometric titration, in which we monitor the titrand’s temperature as we add the titrant, and a potentiometric titration in which we use an ion selective electrode to monitor the metal ion’s concentration as we add the titrant. The experimental approach is essentially identical to that described earlier for an acid–base titration, to which you may refer.

See Chapter 11 for more details about ion selective electrodes.

An important limitation when using an indicator is that we must be able to see the indicator’s change in color at the end point. This may be difficult if the solution is already colored. For example, when titrating Cu²⁺ with EDTA, ammonia is used to adjust the titrand’s pH. The intensely colored Cu(NH₃)₄²⁺ complex obscures the indicator’s color, making an accurate determination of the end point difficult. Other absorbing species present within the sample matrix may also interfere. This is often a problem when analyzing clinical samples, such as blood, or environmental samples, such as natural waters.

If at least one species in a complexation titration absorbs electromagnetic radiation, we can identify the end point by monitoring the titrand’s absorbance at a carefully selected wavelength. For example, we can identify the end point for a titration of Cu²⁺ with EDTA, in the presence of NH₃ by monitoring the titrand’s absorbance at a wavelength of 745 nm, where the Cu(NH₃)₄²⁺ complex absorbs strongly. At the beginning of the titration the absorbance is at a maximum. As we add EDTA, however, the reaction

\[\mathrm{Cu(NH_3)_4^{2+}}(aq)+\textrm Y^{4-}(aq)\rightarrow\textrm{CuY}^{2-}(aq)+4\mathrm{NH_3}(aq)\]

decreases the concentration of Cu(NH₃)₄²⁺ and decreases the absorbance until we reach the equivalence point. After the equivalence point the absorbance remains essentially unchanged. The resulting spectrophotometric titration curve is shown in Figure 9.31a. Note that the titration curve’s y-axis is not the actual absorbance, A, but a corrected absorbance, A_corr

\[A_\textrm{corr}=A\times\dfrac{V_\textrm{EDTA}+V_\textrm{Cu}}{V_\textrm{Cu}}\]

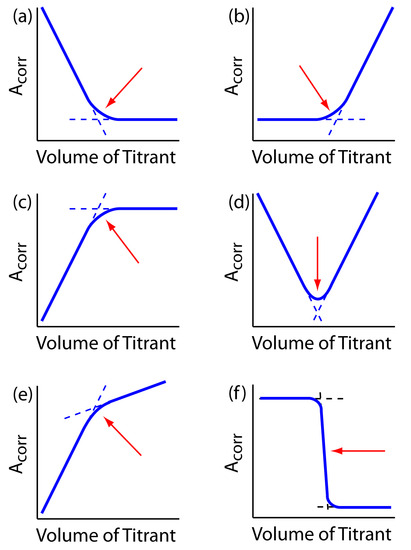
where V_EDTA and V_Cu are, respectively, the volumes of EDTA and Cu. Correcting the absorbance for the titrand’s dilution ensures that the spectrophotometric titration curve consists of linear segments that we can extrapolate to find the end point. Other common spectrophotometric titration curves are shown in Figures 9.31b-f.

Figure 9.31 Examples of spectrophotometric titration curves: (a) only the titrand absorbs; (b) only the titrant absorbs; (c) only the product of the titration reaction absorbs; (d) both the titrand and the titrant absorb; (e) both the titration reaction’s product and the titrant absorb; (f) only the indicator absorbs. The red arrows indicate the end points for each titration curve.

Note

The best way to appreciate the theoretical and practical details discussed in this section is to carefully examine a typical complexation titrimetric method. Although each method is unique, the following description of the determination of the hardness of water provides an instructive example of a typical procedure. The description here is based on Method 2340C as published in Standard Methods for the Examination of Water and Wastewater, 20th Ed., American Public Health Association: Washington, D. C., 1998.

Representative Method 9.2

Determination of Hardness of Water and Wastewater

Description of the Method

The operational definition of water hardness is the total concentration of cations in a sample capable of forming insoluble complexes with soap. Although most divalent and trivalent metal ions contribute to hardness, the most important are Ca²⁺ and Mg²⁺. Hardness is determined by titrating with EDTA at a buffered pH of 10. Calmagite is used as an indicator. Hardness is reported as mg CaCO₃/L.

Procedure

Select a volume of sample requiring less than 15 mL of titrant to keep the analysis time under 5 minutes and, if necessary, dilute the sample to 50 mL with distilled water. Adjust the sample’s pH by adding 1–2 mL of a pH 10 buffer containing a small amount of Mg²⁺–EDTA. Add 1–2 drops of indicator and titrate with a standard solution of EDTA until the red-to-blue end point is reached (Figure 9.32).

Questions

1. Why is the sample buffered to a pH of 10? What problems might you expect at a higher pH or a lower pH?

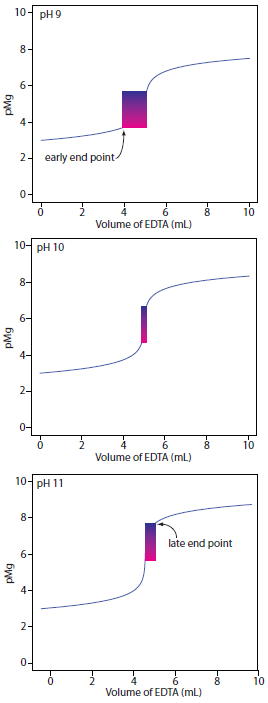
Of the cations contributing to hardness, Mg²⁺ forms the weakest complex with EDTA and is the last cation to be titrated. Calmagite is a useful indicator because it gives a distinct end point when titrating Mg²⁺. Because of calmagite’s acid–base properties, the range of pMg values over which the indicator changes color is pH–dependent (Figure 9.30). Figure 9.33 shows the titration curve for a 50-mL solution of 10^–3 M Mg²⁺ with 10^–2 M EDTA at pHs of 9, 10, and 11. Superimposed on each titration curve is the range of conditions for which the average analyst will observe the end point. At a pH of 9 an early end point is possible, leading to a negative determinate error. A late end point and a positive determinate error are possible if we use a pH of 11.

2. Why is a small amount of the Mg²⁺–EDTA complex added to the buffer?

The titration’s end point is signaled by the indicator calmagite. The indicator’s end point with Mg²⁺ is distinct, but its change in color when titrating Ca²⁺ does not provide a good end point. If the sample does not contain any Mg²⁺ as a source of hardness, then the titration’s end point is poorly defined, leading to inaccurate and imprecise results.

Adding a small amount of Mg²⁺–EDTA to the buffer ensures that the titrand includes at least some Mg²⁺. Because Ca²⁺ forms a stronger complex with EDTA, it displaces Mg²⁺ from the Mg²⁺–EDTA complex, freeing the Mg²⁺ to bind with the indicator. This displacement is stoichiometric, so the total concentration of hardness cations remains unchanged. The displacement by EDTA of Mg²⁺ from the Mg²⁺–indicator complex signals the titration’s end point.

3. Why does the procedure specify that the titration take no longer than 5 minutes?

A time limitation suggests that there is a kinetically controlled interference, possibly arising from a competing chemical reaction. In this case the interference is the possible precipitation of CaCO₃ at a pH of 10.

Figure 9.32 End point for the titration of hardness with EDTA using calmagite as an indicator; the indicator is: (a) red prior to the end point due to the presence of the Mg²⁺–indicator complex; (b) purple at the titration’s end point; and (c) blue after the end point due to the presence of uncomplexed indicator.

Figure 9.33 Titration curves for 50 mL of 10^–3 M Mg²⁺ with 10^–3 M EDTA at pHs 9, 10, and 11 using calmagite as an indicator. The range of pMg and volume of EDTA over which the indicator changes color is shown for each titration curve.

9.3.4 Quantitative Applications

Although many quantitative applications of complexation titrimetry have been replaced by other analytical methods, a few important applications continue to be relevant. In the section we review the general application of complexation titrimetry with an emphasis on applications from the analysis of water and wastewater. First, however, we discuss the selection and standardization of complexation titrants.

Selection and Standardization of Titrants

EDTA is a versatile titrant that can be used to analyze virtually all metal ions. Although EDTA is the usual titrant when the titrand is a metal ion, it cannot be used to titrate anions. In the later case, Ag⁺ or Hg²⁺ are suitable titrants.

Solutions of EDTA are prepared from its soluble disodium salt, Na₂H₂Y•2H₂O and standardized by titrating against a solution made from the primary standard CaCO₃. Solutions of Ag⁺ and Hg²⁺ are prepared using AgNO₃ and Hg(NO₃)₂, both of which are secondary standards. Standardization is accomplished by titrating against a solution prepared from primary standard grade NaCl.

Inorganic Analysis

Complexation titrimetry continues to be listed as a standard method for the determination of hardness, Ca²⁺, CN^–, and Cl^– in waters and wastewaters. The evaluation of hardness was described earlier in Representative Method 9.2. The determination of Ca²⁺ is complicated by the presence of Mg²⁺, which also reacts with EDTA. To prevent an interference the pH is adjusted to 12–13, precipitating Mg²⁺ as Mg(OH)₂. Titrating with EDTA using murexide or Eriochrome Blue Black R as the indicator gives the concentration of Ca²⁺.

Cyanide is determined at concentrations greater than 1 mg/L by making the sample alkaline with NaOH and titrating with a standard solution of AgNO₃, forming the soluble Ag(CN)₂^– complex. The end point is determined using p-dimethylaminobenzalrhodamine as an indicator, with the solution turning from a yellow to a salmon color in the presence of excess Ag⁺.

Chloride is determined by titrating with Hg(NO₃)₂, forming HgCl₂(aq). The sample is acidified to a pH of 2.3–3.8 and diphenylcarbazone, which forms a colored complex with excess Hg²⁺, serves as the indicator. A pH indicator—xylene cyanol FF—is added to ensure that the pH is within the desired range. The initial solution is a greenish blue, and the titration is carried out to a purple end point.

Quantitative Calculations

The quantitative relationship between the titrand and the titrant is determined by the stoichiometry of the titration reaction. For a titration using EDTA, the stoichiometry is always 1:1.

Example 9.7

The concentration of a solution of EDTA was determined by standardizing against a solution of Ca²⁺ prepared using a primary standard of CaCO₃. A 0.4071-g sample of CaCO₃ was transferred to a 500-mL volumetric flask, dissolved using a minimum of 6 M HCl, and diluted to volume. After transferring a 50.00-mL portion of this solution to a 250-mL Erlenmeyer flask, the pH was adjusted by adding 5 mL of a pH 10 NH₃–NH₄Cl buffer containing a small amount of Mg²⁺–EDTA. After adding calmagite as an indicator, the solution was titrated with the EDTA, requiring 42.63 mL to reach the end point. Report the molar concentration of EDTA in the titrant.

(Note that in this example, the analyte is the titrant.)

Solution

The primary standard of Ca²⁺ has a concentration of

\[\dfrac{0.4071\textrm{ g CaCO}_3}{\textrm{0.5000 L}}\times\dfrac{\textrm{1 mol Ca}^{2+}}{100.09\textrm{ g CaCO}_3}=8.135\times10^{-3}\textrm{ M Ca}^{2+}\]

The moles of Ca²⁺ in the titrand is

\[8.135\times10^{-3}\textrm{ M Ca}^{2+}\times0.05000\textrm{ L Ca}^{2+} = 4.068\times10^{-4}\textrm{ mol Ca}^{2+}\]

which means that 4.068×10^–4 moles of EDTA are used in the titration. The molarity of EDTA in the titrant is

\[\mathrm{\dfrac{4.068\times10^{-4}\;mol\;EDTA}{0.04263\;L\;EDTA} = 9.543\times10^{-3}\;M\;EDTA}\]

Practice Exercise 9.14

A 100.0-mL sample is analyzed for hardness using the procedure outlined in Representative Method 9.2, requiring 23.63 mL of 0.0109 M EDTA. Report the sample’s hardness as mg CaCO₃/L.

Click here to review your answer to this exercise.

As shown in the following example, we can easily extended this calculation to complexation reactions using other titrants.

Example 9.8

The concentration of Cl^– in a 100.0-mL sample of water from a freshwater aquifer was tested for the encroachment of sea water by titrating with 0.0516 M Hg(NO₃)₂. The sample was acidified and titrated to the diphenylcarbazone end point, requiring 6.18 mL of the titrant. Report the concentration of Cl^–, in mg/L, in the aquifer.

Solution

The reaction between Cl^– and Hg²⁺ produces a metal–ligand complex of HgCl₂(aq). Each mole of Hg²⁺ reacts with 2 moles of Cl^–; thus

\[\mathrm{\dfrac{0.0516\;mol\;Hg(NO_3)_2}{L}\times0.00618\;L\;Hg(NO_3)_2\times\dfrac{2\;mol\;Cl^-}{mol\;Hg(NO_3)_2}\times\dfrac{35.453\;g\;Cl^-}{mol\;Cl^-}=0.0226\;g\;Cl^-}\]

are in the sample. The concentration of Cl^– in the sample is

\[\dfrac{0.0226\textrm{ g Cl}^-}{0.1000\textrm{ L}}\times\dfrac{\textrm{1000 mg}}{\textrm g}=226\textrm{ mg/L}\]

Practice Exercise 9.15

A 0.4482-g sample of impure NaCN is titrated with 0.1018 M AgNO₃, requiring 39.68 mL to reach the end point. Report the purity of the sample as %w/w NaCN.

Click here to review your answer to this exercise.

Finally, complex titrations involving multiple analytes or back titrations are possible.

Example 9.9

An alloy of chromel containing Ni, Fe, and Cr was analyzed by a complexation titration using EDTA as the titrant. A 0.7176-g sample of the alloy was dissolved in HNO₃ and diluted to 250 mL in a volumetric flask. A 50.00-mL aliquot of the sample, treated with pyrophosphate to mask the Fe and Cr, required 26.14 mL of 0.05831 M EDTA to reach the murexide end point. A second 50.00-mL aliquot was treated with hexamethylenetetramine to mask the Cr. Titrating with 0.05831 M EDTA required 35.43 mL to reach the murexide end point. Finally, a third 50.00-mL aliquot was treated with 50.00 mL of 0.05831 M EDTA, and back titrated to the murexide end point with 6.21 mL of 0.06316 M Cu²⁺. Report the weight percents of Ni, Fe, and Cr in the alloy.

Solution

The stoichiometry between EDTA and each metal ion is 1:1. For each of the three titrations, therefore, we can easily equate the moles of EDTA to the moles of metal ions that are titrated.

Titration 1: moles Ni = moles EDTA

Titration 2: moles Ni + moles Fe = moles EDTA

Titration 3: moles Ni + moles Fe + moles Cr + moles Cu = moles EDTA

We can use the first titration to determine the moles of Ni in our 50.00-mL portion of the dissolved alloy. The titration uses

\[\mathrm{\dfrac{0.05831\;mol\;EDTA}{L}\times 0.02614\;L\;EDTA=1.524\times10^{-3}\;mol\;EDTA}\]

which means the sample contains 1.524×10^–3 mol Ni.

Having determined the moles of EDTA reacting with Ni, we can use the second titration to determine the amount of Fe in the sample. The second titration uses

\[\mathrm{\dfrac{0.05831\;mol\;EDTA}{L}\times0.03543\;L\;EDTA=2.066\times10^{-3}\;mol\;EDTA}\]

of which 1.524×10^–3 mol are used to titrate Ni. This leaves 5.42×10^–4 mol of EDTA to react with Fe; thus, the sample contains 5.42×10^–4 mol of Fe.

Finally, we can use the third titration to determine the amount of Cr in the alloy. The third titration uses

\[\mathrm{\dfrac{0.05831\;mol\;EDTA}{L}\times0.05000\;L\;EDTA=2.916\times10^{-3}\;mol\;EDTA}\]

of which 1.524×10^–3 mol are used to titrate Ni and 5.42×10^–4 mol are used to titrate Fe. This leaves 8.50×10^–4 mol of EDTA to react with Cu and Cr. The amount of EDTA reacting with Cu is

\[\mathrm{\dfrac{0.06316\;mol\;Cu^{2+}}{L}\times0.00621\;L\;Cu^{2+}\times\dfrac{1\;mol\;EDTA}{mol\;Cu^{2+}}=3.92\times10^{-4}\;mol\;EDTA}\]

leaving 4.58×10^–4 mol of EDTA to react with Cr. The sample, therefore, contains 4.58×10^–4 mol of Cr.

Having determined the moles of Ni, Fe, and Cr in a 50.00-mL portion of the dissolved alloy, we can calculate the %w/w of each analyte in the alloy.

\[\mathrm{\dfrac{1.524\times10^{-3}\;mol\;Ni}{50.00\;mL}\times250.0\;mL\times\dfrac{58.69\;g\;Ni}{mol\;Ni}=0.4472\;g\;Ni}\]

\[\mathrm{\dfrac{0.4472\;g\;Ni}{0.7176\;g\;sample}\times100=62.32\%\;w/w\;Ni}\]

\[\mathrm{\dfrac{5.42\times10^{-4}\;mol\;Fe}{50.00\;mL}\times250.0\;mL\times\dfrac{55.847\;g\;Fe}{mol\;Fe}=0.151\;g\;Fe}\]

\[\mathrm{\dfrac{0.151\;g\;Fe}{0.7176\;g\;sample}\times100=21.0\%\;w/w\;Fe}\]

\[\mathrm{\dfrac{4.58\times10^{-4}\;mol\;Cr}{50.00\;mL}\times250.0\;mL\times\dfrac{51.996\;g\;Cr}{mol\;Cr}=0.119\;g\;Cr}\]

\[\mathrm{\dfrac{0.119\;g\;Cr}{0.7176\;g\;sample}\times100=16.6\%\;w/w\;Fe}\]

Practice Exercise 9.16

A indirect complexation titration with EDTA can be used to determine the concentration of sulfate, SO₄^2–, in a sample. A 0.1557-g sample is dissolved in water, any sulfate present is precipitated as BaSO₄ by adding Ba(NO₃)₂. After filtering and rinsing the precipitate, it is dissolved in 25.00 mL of 0.02011 M EDTA. The excess EDTA is then titrated with 0.01113 M Mg²⁺, requiring 4.23 mL to reach the end point. Calculate the %w/w Na₂SO₄ in the sample.

Click here to review your answer to this exercise.

9.3.5 Evaluation of Complexation Titrimetry

The scale of operations, accuracy, precision, sensitivity, time, and cost of a complexation titration are similar to those described earlier for acid–base titrations. Complexation titrations, however, are more selective. Although EDTA forms strong complexes with most metal ion, by carefully controlling the titrand’s pH we can analyze samples containing two or more analytes. The reason we can use pH to provide selectivity is shown in Figure 9.34a. A titration of Ca²⁺ at a pH of 9 gives a distinct break in the titration curve because the conditional formation constant for CaY^2– of 2.6 × 10⁹ is large enough to ensure that the reaction of Ca²⁺ and EDTA goes to completion. At a pH of 3, however, the conditional formation constant of 1.23 is so small that very little Ca²⁺ reacts with the EDTA.

Suppose we need to analyze a mixture of Ni²⁺ and Ca²⁺. Both analytes react with EDTA, but their conditional formation constants differ significantly. If we adjust the pH to 3 we can titrate Ni²⁺ with EDTA without titrating Ca²⁺ (Figure 9.34b). When the titration is complete, we adjust the titrand’s pH to 9 and titrate the Ca²⁺ with EDTA.

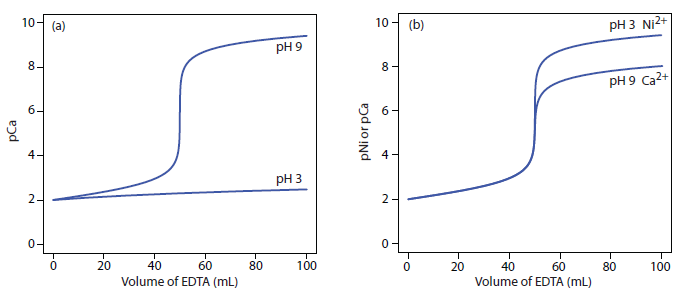
Figure 9.34 Titration curves illustrating how we can use the titrand’s pH to control EDTA’s selectivity. (a) Titration of 50.0 mL of 0.010 M Ca²⁺ at a pH of 3 and a pH of 9 using 0.010 M EDTA. At a pH of 3 the CaY^2– complex is too weak to successfully titrate. (b) Titration of a 50.0 mL mixture of 0.010 M Ca²⁺ and 0.010 M Ni²⁺ at a pH of 3 and a pH of 9 using 0.010 M EDTA. At a pH of 3 EDTA reacts only with Ni²⁺. When the titration is complete, raising the pH to 9 allows for the titration of Ca²⁺.

A spectrophotometric titration is a particularly useful approach for analyzing a mixture of analytes. For example, as shown in Figure 9.35, we can determine the concentration of a two metal ions if there is a difference between the absorbance of the two metal-ligand complexes.

Figure 9.35 Spectrophotometric titration curve for the complexation titration of a mixture of two analytes. The red arrows indicate the end points for each analyte.

Contributors

David Harvey (DePauw University)