6.E: Equilibrium Chemistry (Exercises)

Most of the problems that follow require one or more equilibrium constants or standard state potentials. For your convenience, here are hyperlinks to the appendices containing these constants

• Appendix 10: Solubility Products
• Appendix 11: Acid Dissociation Constants
• Appendix 12: Metal-Ligand Formation Constants
• Appendix 13: Standard State Reduction Potentials

1. Write equilibrium constant expressions for the following reactions. What is the value for each reaction’s equilibrium constant?

1. NH₃(aq) + HCl(aq) ⇋ NH₄⁺(aq) + Cl⁻(aq)
2. PbI₂(s) + S²⁻(aq) ⇋ PbS(s) + 2I⁻(aq)
3. Cd(EDTA)²⁻(aq) + 4CN⁻(aq) ⇋ Cd(CN)₄²⁻(aq) + EDTA⁴⁻(aq)
4. AgCl(s) + 2NH₃(aq) ⇋ Ag(NH₃)₂⁺(aq) + Cl⁻(aq)
5. BaCO₃(s) + H₃O⁺(aq) ⇋ Ba²⁺(aq) + H₂CO₃(aq) + H₂O(l)

2. Using a ladder diagram, explain why the first reaction is favorable and the second reaction is unfavorable.

\[\mathrm{H_3PO_4}(aq)+\mathrm{F^-}(aq)\rightleftharpoons\mathrm{HF}(aq)+\ce{H_2PO_4^-}(aq)\]

\[\mathrm{H_3PO_4}(aq)+\mathrm{2F^-}(aq)\rightleftharpoons\mathrm{2HF}(aq)+\mathrm{HPO_4^{2-}}(aq)\]

Determine the equilibrium constant for these reactions and verify that they are consistent with your ladder diagram.

3. Calculate the potential for the following redox reaction for a solution in which [Fe³⁺] = 0.050 M, [Fe²⁺] = 0.030 M, [Sn²⁺] = 0.015 M and [Sn⁴⁺] = 0.020 M.

\[\mathrm{2Fe^{3+}}(aq)+\mathrm{Sn^{2+}}(aq)\rightleftharpoons\mathrm{Sn^{4+}}(aq)+\mathrm{2Fe^{2+}}(aq)\]

4. Calculate the standard state potential and the equilibrium constant for each of the following redox reactions. Assume that [H₃O⁺] is 1.0 M for acidic solutions, and that [OH⁻] is 1.0 M for basic solutions.

1. MnO₄⁻(aq) + H₂SO₃(aq) ⇋ Mn²⁺(aq) + SO₄²⁻ acidic solution
2. IO₃⁻(aq) + I⁻(aq) ⇋ I₂(s) acidic solution
3. ClO⁻(aq) + I⁻(aq) ⇋ IO₃⁻(aq) + Cl⁻(aq) basic solution

These redox reactions in this problem are not balanced. You will need to balance the reactions before calculating their standard state potentials. Although you may recall how to do this from another course, there is a much easier approach that you can use here. Identify the oxidizing agent and the reducing agent and divide the reaction into two unbalanced half-reactions. Using Appendix 13, find the appropriate balanced half-reactions. Add the two half-reactions together and simplify the stoichiometry to arrive at the balanced redox reaction.

As an example, in (a) the oxidizing agent is MnO₄⁻ and its unbalanced half-reaction is

\[\ce{MnO_4^-}(aq)+5e^-\rightleftharpoons\mathrm{Mn^{2+}}(aq)\]

The corresponding balanced half-reaction from Appendix 13 is

\[\ce{MnO_4^-}(aq)+\mathrm{8H^+}(aq)+5e^-\rightleftharpoons\mathrm{Mn^{2+}}(aq)+\mathrm{4H_2O}(l)\]

5. One analytical method for determining the concentration of sulfur is to oxidize it to SO₄^2- and then precipitate it as BaSO₄ by adding BaCl₂. The mass of the resulting precipitate is proportional to the amount of sulfur in the original sample. The accuracy of this method depends on the solubility of BaSO₄, the reaction for which is shown here.

\[\mathrm{BaSO_4}(s)\rightleftharpoons\mathrm{Ba^{2+}}(aq)+\mathrm{SO_4^{2-}}(aq)\]

How do the following affect the solubility of BaSO₄ and, therefore, the accuracy of the analytical method?

a. decreasing the solution’s pH
b. adding more BaCl₂
c. increasing the volume of the solution by adding H₂O

6. Write a charge balance equation and mass balance equations for the following solutions. Some solutions may have more than one mass balance equation.

a. 0.10 M NaCl
b. 0.10 M HCl
c. 0.10 M HF
d. 0.10 M NaH₂PO₄
e. MgCO₃ (saturated solution)
f. 0.10 M Ag(CN)₂^–
g. 0.10 M HCl and 0.050 M NaNO₂

7. Using the systematic approach to equilibrium problems, calculate the pH of the following solutions. Be sure to state and justify any assumptions you make in solving the problems.

a. 0.050 M HClO₄
b. 1.00 × 10^–7 M HCl
c. 0.025 M HClO
d. 0.010 M HCOOH
e. 0.050 M Ba(OH)₂
f. 0.010 M C₅H₅N

8. Construct ladder diagrams for the following diprotic weak acids (H₂L) and estimate the pH of 0.10 M solutions of H₂L, HL^– and L^2–.

a. maleic acid
b. malonic acid
c. succinic acid

9. Using the systematic approach to solving equilibrium problems, calculate the pH of the diprotic weak acid in problem 8. Be sure to state and justify any assumptions you make in solving the problems.

10. Ignoring activity effects, calculate the concentration of Hg₂²⁺ in the following solutions. Be sure to state and justify any assumption you make in solving the problems.

a. a saturated solution of Hg₂Br₂
b. 0.025 M Hg₂(NO₃)₂ saturated with Hg₂Br₂
c. 0.050 M NaBr saturated with Hg2Br2

11. The solubility of CaF₂ is controlled by the following two reactions

\[\mathrm{CaF_2}(s)\rightleftharpoons\mathrm{Ca^{2+}}(aq)+\mathrm{2F^-}(aq)\]

\[\mathrm{HF}(aq)+\mathrm{H_2O}(l)\rightleftharpoons\mathrm{H_3O^+}(aq)+\mathrm{F^-}(aq)\]

Calculate the solubility of CaF₂ in a solution buffered to a pH of 7.00. Use a ladder diagram to help simplify the calculations. How would your approach to this problem change if the pH is buffered to 2.00? What is the solubility of CaF₂ at this pH? Be sure to state and justify any assumptions you make in solving the problems.

12. Calculate the solubility of Mg(OH)₂ in a solution buffered to a pH of 7.00. How does this compare to its solubility in unbuffered deionized water? Be sure to state and justify any assumptions you make in solving the problem.

13. Calculate the solubility of Ag₃PO₄ in a solution buffered to a pH of 7.00. Be sure to state and justify any assumptions you make in solving the problem.

14. Determine the equilibrium composition of saturated solution of AgCl. Assume that the solubility of AgCl is influenced by the following reactions.

\[\mathrm{AgCl}(s)\rightleftharpoons\mathrm{Ag^+}(aq)+\mathrm{Cl^-}(aq)\]

\[\mathrm{Ag^+}(aq)+\mathrm{Cl^-}(aq)\rightleftharpoons\mathrm{AgCl}(aq)\]

\[\mathrm{AgCl}(aq)+\mathrm{Cl^-}(aq)\rightleftharpoons\ce{AgCl_2^-}(aq)\]

Be sure to state and justify any assumptions you make in solving the problem.

15. Calculate the ionic strength of the following solutions

a. 0.050 M NaCl
b. 0.025 M CuCl₂
c. 0.10 M Na₂SO₄

16. Repeat the calculations in problem 10, this time correcting for the effect of ionic strength. Be sure to state and justify any assumptions you make in solving the problems.

17. Over what pH range do you expect Ca₃(PO₄)₂ to have its minimum solubility?

18. Construct ladder diagrams for the following systems, each consisting of two or three equilibria. Using your ladder diagrams, what reactions are likely to occur in each system?

a. HF and H₃PO₄
b. Ag(CN)₂^–, Ni(CN)₄^2– and Fe(CN)₆^3–
c. Cr₂O₇^2–/Cr³⁺ and Fe³⁺/Fe²⁺

19. Calculate the pH of the following acid–base buffers. Be sure to state and justify any assumptions you make in solving the problems.

a. 100 mL of 0.025 M formic acid and 0.015 M sodium formate
b. 50.00 mL of 0.12 M NH₃ and 5.30 mL of 1.0 M HCl
c. 5.00 g of Na₂CO₃ and 5.00 g of NaHCO₃ diluted to 100 mL

20. Calculate the pH of the buffers in problem 19 after adding 5.0 mL of 0.10 M HCl. Be sure to state and justify any assumptions you make in solving the problems.

21. Calculate the pH of the buffers in problem 19 after adding 5.0 mL of 0.10 M NaOH. Be sure to state and justify any assumptions you make in solving the problems.

22. Consider the following hypothetical complexation reaction between a metal, M, and a ligand, L

\[\mathrm{M}(aq)+\mathrm{L}(aq)\rightleftharpoons\mathrm{ML}(aq)\]

with a formation constant of 1.5 × 10⁸. Derive an equation, similar to the Henderson–Hasselbalch equation, relating pM to the concentrations of L and ML. What is the pM for a solution containing 0.010 mol of M and 0.020 mol of L? What is pM be if you add 0.002 mol of M to this solution? Be sure to state and justify any assumptions you make in solving the problem.

23. A redox buffer contains an oxidizing agent and its conjugate reducing agent. Calculate the potential of a solution containing 0.010 mol of Fe³⁺ and 0.015 mol of Fe²⁺. What is the potential if you add sufficient oxidizing agent to convert 0.002 mol of Fe²⁺ to Fe³⁺? Be sure to state and justify any assumptions you make in solving the problem.

24. Use either Excel or R to solve the following problems. For these problems, make no simplifying assumptions.
a. the solubility of CaF₂ in deionized water
b. the solubility of AgCl in deionized water (see Problem 14 for the relevant equilibria)
c. the pH of 0.10 M fumaric acid

25. Beginning with the relevant equilibrium reactions, derive equation 6.64 for the rigorous solution to the pH of 0.1 M HF.

6.12.3 Solutions to Practice Exercises

Practice Exercise 6.1

The overall reaction is equivalent to

\[\mathrm{Rxn\;4-2\times Rxn\;1}\]

Subtracting a reaction is equivalent to adding the reverse reaction; thus, the overall equilibrium constant is

\[K=\dfrac{K_4}{(K_1)^2}=\dfrac{5.0}{(0.40)^2}=31.25\approx31\]

Click here to return to the chapter.

Practice Exercise 6.2

The K_b for hydrogen oxalate is

\[K_\mathrm{b,HC_2O_4^-}{}=\dfrac{K_\mathrm w}{K_\mathrm{a,H_2C_2O_4}}=\dfrac{1.00\times10^{-14}}{5.60\times10^{-2}}=1.79\times10^{-13}\]

and the K_b for oxalate is

\[K_\mathrm{b,C_2O_4^{2-}}=\dfrac{K_\mathrm w}{K_\mathrm{a,HC_2O_4^-}}=\dfrac{1.00\times10^{-14}}{5.42\times10^{-5}}=1.85\times10^{-10}\]

As we expect, the K_b value for C₂O₄^2– is larger than that for HC₂O₄^–.

Click here to return to the chapter.

Practice Exercise 6.3

We can write the reaction as a sum of three other reactions. The first reaction is the solubility of AgCl(s), which we characterize by its K_sp.

\[\mathrm{AgBr}(s)\rightleftharpoons\mathrm{Ag^+}(aq)+\mathrm{Br^-}(aq)\]

The remaining two reactions are the stepwise formation of Ag(S₂O₃)₂^3–, which we characterize by K₁ and K₂.

\[\mathrm{Ag^+}(aq)+\mathrm{S_2O_3^{2-}}(aq)\rightleftharpoons\mathrm{Ag(S_2O_3)^-}(aq)\]

\[\mathrm{Ag(S_2O_3)^-}(aq)+\mathrm{S_2O_3^{2-}}(aq)\rightleftharpoons\mathrm{Ag(S_2O_3)_2^{3-}}(aq)\]

Using values for K_sp, K₁, and K₂ from Appendix 10 and Appendix 11, we find that the equilibrium constant for our reaction is

\[K=K_\mathrm{sp}\times K_1\times K_2=(5.0\times10^{-13})(6.6\times10^8)(7.1\times10^4)=23\]

Click here to return to the chapter.

Practice Exercise 6.4

The two half-reactions are the oxidation of Fe²⁺ and the reduction of MnO₄^–.

\[\mathrm{Fe^{2+}}(aq)\rightleftharpoons\mathrm{Fe^{3+}}(aq)+e^-\]

\[\ce{MnO_4^-}(aq)+\mathrm{8H^+}(aq)+5e^-\rightleftharpoons\mathrm{Mn^{2+}}(aq)+\mathrm{4H_2O}(l)\]

From Appendix 13, the standard state reduction potentials for these half-reactions are

\[E^\circ_\mathrm{Fe^{3+}/Fe^{2+}}=0.771 \textrm{ V} \hspace{10mm}E^\circ_\mathrm{MnO_4^-/Mn^{2+}}=1.51\textrm{ V}\]

(a) The standard state potential for the reaction is

\[E^\circ=E^\circ_\mathrm{MnO_4^-/Mn^{2+}}-E^\circ_\mathrm{Fe^{3+}/Fe^{2+}}=\mathrm{1.51\;V-0.771\;V=0.74\;V}\]

(b) To calculate the equilibrium constant we substitute appropriate values into equation 6.25.

\[E^\circ=0.74\;\mathrm V=\dfrac{0.05916}{5}\log K\]

Solving for K gives its value as

\[\log K=62.5\hspace{10mm}K=3.2\times10^{62}\]

(c) To calculate the potential under these non-standard state conditions, we make appropriate substitutions into the Nernst equation.

\[E=E^\circ-\dfrac{RT}{nF}\ln\mathrm{\dfrac{[Mn^{2+}][Fe^{3+}]^5}{[\ce{MnO_4^-}][Fe^{2+}]^5[H^+]^8}}\]

\[E=0.74-\dfrac{0.05916}{5}\log\dfrac{(0.015)(0.10)^5}{(0.025)(0.50)^5(1\times10^{-7})^8}\]

\[E=0.74-\dfrac{0.05916}{5}\log\dfrac{(0.015)(0.10)^5}{(0.025)(0.50)^5(1\times10^{-7})^8}=0.12\textrm{ V}\]

Click here to return to the chapter.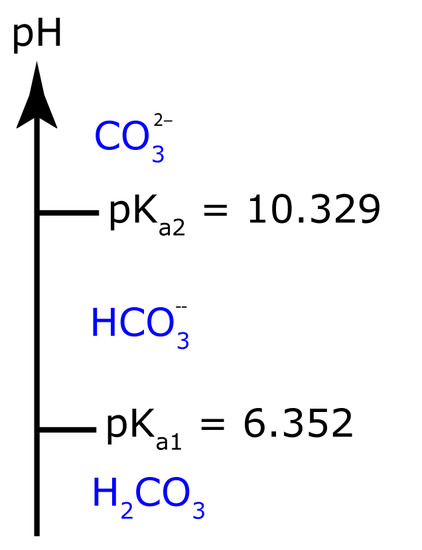

Practice Exercise 6.5

From Appendix 11, the pK_a values for H₂CO₃ are 6.352 and 10.329. The ladder diagram for H₂CO₃ is shown to the side. The predominate form at a pH of 7.00 is HCO₃^–.

Click here to return to the chapter.

Practice Exercise 6.6

The ladder diagram in Figure 6.5 indicates that the reaction between acetic acid and p-nitrophenolate is favorable. Because p-nitrophenolate is in excess, we assume that the reaction of acetic acid to acetate is complete. At equilibrium essentially no acetic acid remains and there are 0.040 moles of acetate. Converting acetic acid to acetate consumes 0.040 moles of p-nitrophenolate; thus

\[\textrm{moles }p\textrm{-nitrophenolate}=0.090-0.040=0.050\textrm{ mol}\]

\[\textrm{moles }p\textrm{-nitrophenol = 0.040 mol}\]

According to the ladder diagram for this system, the pH is 7.15 when there are equal concentrations of p-nitrophenol and p-nitrophenolate. Because we have slightly more p-nitrophenolate than we have p-nitrophenol, the pH is slightly greater than 7.15.

Click here to return to the chapter.

Practice Exercise 6.7

As Hg₂Cl₂ dissolves, two Cl^– are produced for each ion of Hg₂²⁺. If we assume that x is the change in the molar concentration of Hg₂²⁺, then the change in the molar concentration of Cl^– is 2x. The following table helps us keep track of our solution to this problem.

Concentrations	Hg2Cl2(s)	⇋	Hg2^2+(aq)	+	2Cl^–(aq)
Initial Change	solid solid		0 +x		0 +2x
Equilibrium	solid		x		2x

Substituting the equilibrium concentrations into the K_sp expression for Hg₂Cl₂ gives

\[K_\textrm{sp}=\mathrm{[Hg_2^{2+}][Cl^-]^2}=(x)(2x)^2=4x^3=1.2\times10^{-18}\]

\[x=6.69\times10^{-7}\]

Substituting x back into the equilibrium expressions for Hg₂²⁺ and Cl^– gives their concentrations as

\[\mathrm{[Hg_2^{2+}]}=x=6.7\times10^{-7}\textrm{ M}\hspace{10mm}\mathrm{[Cl^-]}=2x=1.3\times10^{-6}\textrm{ M}\]

The molar solubility is equal to [Hg₂²⁺], or 6.7 × 10^–7 mol/L.

Click here to return to the chapter.

Practice Exercise 6.8

We begin by setting up a table to help us keep track of the concentrations of Hg₂²⁺ and Cl^– as this system moves toward and reaches equilibrium.

Concentrations	Hg2Cl2(s)	⇋	Hg2^2+(aq)	+	2Cl^–(aq)
Initial Change	solid solid		0 +x		0.10 +2x
Equilibrium	solid		x		0.10 + 2x

Substituting the equilibrium concentrations into the K_sp expression for Hg₂Cl₂ leaves us with a difficult to solve cubic equation.

\[K_\mathrm{sp}=\mathrm{[Hg_2^{2+}][Cl^-]^2}=(x)(0.10)^2=4x^3+0.40x^2+0.10x\]

Let’s make an assumption to simplify this problem. Because we expect the value of x to be small, let’s assume that

\[\mathrm{[Cl^-]}=0.10+x\approx0.10\textrm{ M}\]

This simplifies our problems to

\[K_\mathrm{sp}=\mathrm{[Hg_2^{2+}][Cl^-]^2}=(x)(0.10)^2=0.010x=1.2\times10^{-18}\]

which gives the value of x as

\[x=1.2\times10^{-16}\textrm{ M}\]

The difference between the actual concentration of Cl^–, which is (0.10 + x) M, and our assumption that it is 0.10 M introduces an error of 1.2 × 10^–14 %. This is a negligible error. The molar solubility of Hg₂Cl₂ is the same as the concentration of Hg₂²⁺, or 1.2 × 10^–16 M. As expected, the molar solubility in 0.10 M NaCl is less than 6.7 × 10^–7 mol/L, which is its solubility in water (see solution to Practice Exercise 6.7).

Click here to return to the chapter.

Practice Exercise 6.9

To help us in determining what ions are in solution, let’s write down all the reaction leading to the preparation of the solutions and the equilibria within the solutions. These reactions are the dissolution of two soluble salts

\[\mathrm{KH_2PO_4}(s)\rightarrow\mathrm{K^+}(aq)+\ce{H_2PO_4^-}(aq)\]

\[\mathrm{Na_2HPO_4}(s)\rightarrow\mathrm{2Na^+}(aq)+\mathrm{HPO_4^{2-}}(aq)\]

and the acid–base dissociation reactions for H₂PO₄^–, HPO₄^2–, and H₂O.

\[\ce{H_2PO_4^-}(aq)+\mathrm{H_2O}(l)\rightleftharpoons\mathrm{H_3O^+}(aq)+\mathrm{HPO_4^{2-}}(aq)\]

\[\ce{H_2PO_4^-}(aq)+\mathrm{H_2O}(l)\rightleftharpoons\mathrm{OH^-}(aq)+\mathrm{H_3PO_4}(aq)\]

\[\mathrm{HPO_4^{2-}}(aq)+\mathrm{H_2O}(l)\rightleftharpoons\mathrm{H_3O^+}(aq)+\mathrm{PO_4^{3-}}(aq)\]

\[\mathrm{2H_2O}(l)\rightleftharpoons\mathrm{H_3O^+}(aq)+\mathrm{OH^-}(aq)\]

Note that we did not include the base dissociation reaction for HPO₄^2– because we already have accounted for its product, H₂PO₄^–, in another reaction. The mass balance equations for K⁺ and Na⁺ are straightforward

\[\mathrm{[K^+]=0.10\;M\hspace{8mm}[Na^+]=0.10\;M}\]

but the mass balance equation for the phosphate takes a little bit of thought. Both H₂PO₄^– and HPO₄^2– produce the same ions in solution. We can, therefore, imagine that the solution initially contains 0.15 M KH₂PO₄, which gives the following mass balance equation.

\[\mathrm{0.15\;M=[H_3PO_4]+[\ce{H_2PO_4^-}]+[HPO_4^{2-}]+[PO_4^{3-}]}\]

The charge balance equation is

\[\mathrm{[H_3O^+]+[K^+]+[Na^+]=[\ce{H_2PO_4^-}]+2\times[HPO_4^{2-}]+3\times[PO_4^{3-}]+[OH^-]}\]

Click here to return to the chapter.

Practice Exercise 6.10

In determining the pH of 0.050 M NH₃, we need to consider two equilibrium reactions—the base dissociation reaction for NH₃

\[\mathrm{NH_3}(aq)+\mathrm{H_2O}(l)\rightleftharpoons\mathrm{OH^-}(aq)+\mathrm{NH_4^+}(aq)\]

and water’s dissociation reaction.

\[\mathrm{2H_2O}(l)\rightleftharpoons\mathrm{H_3O^+}(aq)+\mathrm{OH^-}(aq)\]

These two reactions contain four species whose concentrations we need to consider: NH₃, NH₄⁺, H₃O⁺, and OH^–. We need four equations to solve the problem—these equations are the K_b equation for NH₃

\[K_\mathrm b=\mathrm{\dfrac{[OH^-][NH_4^+]}{[NH_3]}}=1.75\times10^{-5}\]

the K_w equation for H₂O

\[K_\mathrm w=\mathrm{[H_3O^+][OH^-]}=1.00\times10^{-14}\]

a mass balance on ammonia

\[C_\mathrm{NH_3}=\mathrm{0.050\;M=[NH_3]+[NH_4^+]}\]

and a charge balance equation

\[\mathrm{[H_3O^+]+[NH_4^+]=[OH^-]}\]

To solve this problem, we will make two assumptions. Because NH₃ is a base, our first assumption is

\[\mathrm{[OH^-]>>[H_3O^+]}\]

which simplifies the charge balance equation to

\[\mathrm{[NH_4^+]=[OH^-]}\]

Because NH₃ is a weak base, our second assumption is

\[\mathrm{[NH_3]>>[NH_4^+]}\]

which simplifies the mass balance equation to

\[C_\mathrm{NH_3}=\mathrm{0.050\;M=[NH_3]}\]

Substituting the simplified charge balance equation and mass balance equation into the K_b equation leave us with

\[K_\mathrm b=\dfrac{\mathrm{[OH^-][OH^-]}}{C_\mathrm{NH_3}}=\dfrac{\mathrm{[OH^-]^2}}{C_\mathrm{NH_3}}=1.75\times10^{-5}\]

\[\mathrm{[OH^-]}=\sqrt{K_\mathrm bC_\mathrm{NH_3}}=\sqrt{(1.75\times10^{-5})(0.050)}=9.35\times10^{-4}\]

Before accepting this answer, we must verify our two assumptions. The first assumption is that the concentration of OH^– is significantly greater than the concentration of H₃O⁺. Using K_w, we find that

\[\mathrm{[H_3O^+]}=\dfrac{K_\mathrm w}{\mathrm{[OH^-]}}=\dfrac{1.00\times10^{-14}}{9.35\times10^{-4}}=1.07\times10^{-11}\]

Clearly this assumption is acceptable. Our second assumption is that the concentration of NH₃ is scientifically greater than the concentration of NH₄⁺. Using our simplified charge balance equation, we find that

\[\mathrm{[NH_4^+]=[OH^-]=9.35\times10^{-4}}\]

Because the concentration of NH₄⁺ is 1.9% of C_NH3, our second assumption also is reasonable. Given that [H₃O⁺] is 1.07 × 10^–11, the pH is 10.97.

Click here to return to the chapter.

Practice Exercise 6.11

In solving for the pH of 0.10 M alanine, we made the following three assumptions.

\[\textrm{Assumption One: }\mathrm{[HL]>>[H_2L^+]+[L^-]}\]

\[\textrm{Assumption Two: }K_\mathrm{a1}K_\mathrm w << K_\mathrm{a1}K_\mathrm{a2}C_\mathrm{HL}\]

\[\textrm{Assumption Three: }K_\mathrm{a1}<<C_\mathrm{HL}\]

The second and third assumptions are easy to check. The value for K_a1 (4.487 × 10^–3) is 0.45% of C_HL (0.10), and K_a1 × K_w (4.487 × 10^–17) is 0.074% of K_a1 × K_a2 × C_HL (6.093 × 10^–14). Each assumption introduces an error of less than ±5%.

To test the first assumption, we need to calculate the concentrations of H₂L⁺ and L^–, which we accomplish using the equations for K_a1 and K_a2.

\[\mathrm{[H_2L^+]=\dfrac{[H_3O^+][HL]}{\mathit K_{a1}}=\dfrac{(7.807\times10^{-7})(0.10)}{4.487\times10^{-3}}=1.74\times10^{-5}}\]

\[\mathrm{[L^-]=\dfrac{\mathit K_{a2}[HL]}{[H_3O^+]}=\dfrac{(1.358\times10^{-10})(0.10)}{7.807\times10^{-7}}=1.74\times10^{-5}}\]

Because these concentrations are less than ±5% of C_HL, the first assumption also is acceptable.

Click here to return to the chapter.

Practice Exercise 6.12

The acid dissociation constant for H₂PO₄^– is 6.32 × 10^–8, or a pK_a of 7.199. Substituting the initial concentrations of H₂PO₄^– and HPO₄^2– into equation 6.60 and solving gives the buffer’s pH as

\[\mathrm{pH=7.199+\log\dfrac{[HPO_4^{2-}]}{[\ce{H_2PO_4^-}]}=7.199+\log\dfrac{0.050}{0.10}=6.898\approx6.90}\]

Adding HCl converts a portion of HPO₄^2– to H₂PO₄^– as a result of the following reaction

\[\mathrm{HPO_4^{2-}}(aq)+\mathrm{H_3O^+}(aq)\rightleftharpoons\mathrm{H_2O}(l)+\ce{H_2PO_4^-}(aq)\]

Because this reaction’s equilibrium constant is so large (it is 1.59 × 10⁷), we may treat the reaction as if it goes to completion. The new concentrations of H₂PO₄^– and HPO₄^2– are

\[\begin{align}
C_\mathrm{H_2PO_4^-} &=\dfrac{\mathrm{mol\;\ce{H_2PO_4^-}+mol\;HCl}}{V_\mathrm{total}}\\
&\mathrm{=\dfrac{(0.10\;M)(010\;L)+(0.20\;M)(5.0\times10^{-3}\;L)}{0.10\;L+5.0\times10^{-3}\;L}=0.105\;M}\\
C_\mathrm{HPO_4^{2-}}&=\dfrac{\mathrm{mol\;HPO_4^{2-}-mol\;HCl}}{V_\mathrm{total}}\\
&\mathrm{=\dfrac{(0.05\;M)(010\;L)-(0.20\;M)(5.0\times10^{-3}\;L)}{0.10\;L+5.0\times10^{-3}\;L}=0.0381\;M}
\end{align}\]

Substituting these concentrations into equation 6.60 gives a pH of

\[\mathrm{pH=7.199+\log\dfrac{[HPO_4^{2-}]}{[\ce{H_2PO_4^-}]}=7.199+\log\dfrac{0.0381}{0.105}=6.759\approx6.76}\]

As we expect, adding HCl decreases the buffer’s pH by a small amount, dropping from 6.90 to 6.76.

Click here to return to the chapter.

Practice Exercise 6.13

We begin by calculating the solution’s ionic strength. Because NaCl is a 1:1 ionic salt, the ionic strength is the same as the concentration of NaCl; thus μ = 0.10 M. This assumes, of course, that we can ignore the contributions of Hg₂²⁺ and Cl^– from the solubility of Hg₂Cl₂.

Next we use equation 6.63 to calculate the activity coefficients for Hg₂²⁺ and Cl^–.

\[\begin{align}
\log\gamma_\mathrm{Hg_2^{2+}}&=\dfrac{-0.51\times(+2)^2\times\sqrt{0.10}}{1+3.3\times0.40\times\sqrt{0.10}}=-0.455\\
\gamma_\mathrm{Hg_2^{2+}}&=0.351\\
\log\gamma_\mathrm{Cl^-}&=\dfrac{-0.51\times(-1)^2\times\sqrt{0.10}}{1+3.3\times0.3\times\sqrt{0.10}}=-0.12\\
\gamma_\mathrm{Cl^-}&=0.75
\end{align}\]

Defining the equilibrium concentrations of Hg₂²⁺ and Cl^– in terms of the variable x

Concentrations	Hg2Cl2(s)	⇋	Hg2^2^+(aq)	+	2Cl^–(aq)
Initial Change	solid solid		0 +x		0.10 +2x
Equilibrium	solid		x		0.10 + 2x

and substituting into the thermodynamic solubility product for Hg₂Cl₂, leave us with

\[K_\mathrm{sp}=a_\mathrm{Hg_2^{2+}}a_\mathrm{Cl^-}^2=\mathrm{\gamma_{Hg_2^{2+}}[Hg_2^{2+}]\gamma_{Cl^-}^2[Cl^-]^2=1.2\times10^{-18}}\]

\[1.2\times10^{-18}=(0.351)(x)(0.75)^2(0.10+x)^2\]

Because the value of x is likely to be small, let’s simplify this equation to

\[1.2\times10^{-18}=(0.351)(x)(0.75)^2(0.10)^2\]

Solving for x gives its value as 6.1 × 10^–16. Because x is the concentration of Hg₂²⁺ and 2x is the concentration of Cl^–, our decision to ignore their contributions to the ionic strength is reasonable. The molar solubility of Hg₂Cl₂ in 0.10 M NaCl is 6.1 × 10^–16 mol/L. In Practice Exercise 6.8, where we ignored ionic strength, we determined that the molar solubility of Hg₂Cl₂ is 1.2 × 10^–16 mol/L, a result that is 5× smaller than the its actual value.

Click here to return to the chapter.

Practice Exercise 6.14

To solve this problem, let’s set up the following spreadsheet

copying the contents of cells B1-B9 into several additional columns. See our earlier treatment of this problem for the relevant equilibrium reactions and equilibrium constants. The initial guess for pI in cell B1 gives the concentration of I^– in cell B2. Cells B3–B8 calculate the remaining concentrations, using the K_sp to obtain [Ag⁺], using the mass balance on iodide and silver to obtain [Ag(NH₃)₂⁺], using β₂ to calculate [NH₃], using the mass balance on ammonia to find [NH₄⁺], using K_b to calculate [OH⁻], and using K_w to calculate [H₃O⁺]. The system’s charge balance equation provides a means for determining the calculation’s error.

\[\mathrm{[Ag^+]+[Ag(NH_3)_2^+]+[NH_4^+]+[H_3O^+]-[I^-]-[OH^-]=0}\]

The largest possible value for pI—corresponding to the smallest concentration of I^– and the lowest possible solubility—occurs for a simple, saturated solution of AgI. When [Ag⁺] = [I⁻], the concentration of iodide is

\[\mathrm{[I^-]}=\sqrt{K_\mathrm{sp}}=\sqrt{8.3\times10^{-17}}=9.1\times10^{-9}\textrm{ M}\]

corresponding to a pI of 8.04. Entering initial guesses for pI of 4, 5, 6, 7, and 8 shows that the error changes sign between a pI of 5 and 6. Continuing in this way to narrow down the range for pI, we find that the error function is closest to zero at a pI of 5.42. The concentration of I^– at equilibrium, and the molar solubility of AgI, is 3.8 × 10^–6 mol/L, which agrees with our earlier solution to this problem.

Click here to return to the chapter.

Practice Exercise 6.15

To solve this problem, let’s use the following function

> eval=function(pI){

+ I=10^–pI

+ Ag=8.3e–17/I

+ AgNH3=Ag–I

+ NH3=(AgNH3/(1.7e7*Ag))^0.5

+ NH4=0.10‑NH3–2*AgNH3

+ OH=1.75e–5*NH3/NH4

+ H3O=1e–14/OH

+ error=Ag+AgNH3+NH4+H3O–OH–I

+ output=data.frame(pI,error)

+ print(output)

+ }

The function accepts an initial guess for pI and calculates the concentrations of species in solution using the definition of pI to calculate [I⁻], using the K_sp to obtain [Ag⁺], using the mass balance on iodide and silver to obtain [Ag(NH₃)₂⁺], using β₂ to calculate [NH₃], using the mass balance on ammonia to find [NH₄⁺], using K_b to calculate [OH⁻], and using K_w to calculate [H₃O⁺]. The system’s charge balance equation provides a means for determining the calculation’s error.

\[\mathrm{[Ag^+]+[Ag(NH_3)_2^+]+[NH_4^+]+[H_3O^+]-[I^-]-[OH^-]=0}\]

The largest possible value for pI—corresponding to the smallest concentration of I^– and the lowest possible solubility—occurs for a simple, saturated solution of AgI. When [Ag⁺] = [I⁻], the concentration of iodide is

\[\mathrm{[I^-]}=\sqrt{K_\mathrm{sp}}=\sqrt{8.3\times10^{-17}}=9.1\times10^{-9}\textrm{ M}\]

corresponding to a pI of 8.04. The following session shows the function in action.

> pI =c(4, 5, 6, 7, 8)
> eval(pI)
pI error
1 4 -2.56235615
2 5 -0.16620930
3 6 0.07337101
4 7 0.09734824
5 8 0.09989073
> pI =c(5.1, 5.2, 5.3, 5.4, 5.5, 5.6, 5.7, 5.8, 5.9, 6.0)
> eval(pI)
pI error
1 5.1 -0.11144658
2 5.2 -0.06794105
3 5.3 -0.03336475
4 5.4 -0.00568116
5 5.5 0.01571549
6 5.6 0.03308929
7 5.7 0.04685937
8 5.8 0.05779214
9 5.9 0.06647475
10 6.0 0.07337101
> pI =c(5.40, 5.41, 5.42, 5.43, 5.44, 5.45, 5.46, 5.47, 5.48, 5.49, 5.50)
> eval(pI)
pI error
1 5.40 -0.0056811605
2 5.41 -0.0030715484
3 5.42 0.0002310369
4 5.43 -0.0005134898
5 5.44 0.0028281878
6 5.45 0.0052370980
7 5.46 0.0074758181
8 5.47 0.0096260370
9 5.48 0.0117105498
10 5.49 0.0137387291
11 5.50 0.0157154889

The error function is closest to zero at a pI of 5.42. The concentration of I^– at equilibrium, and the molar solubility of AgI, is 3.8 × 10^–6 mol/L, which agrees with our earlier solution to this problem.

Click here to return to the chapter

References

1. Quilez, J. Chem. Educ. Res. Pract. 2004, 5, 69–87 (www.uoi.gr/cerp).
2. lthough not specifically on the topic of ladder diagrams as developed in this section, the following sources provide appropriate background information: (a) Runo, J. R.; Peters, D. G. J. Chem. Educ. 1993, 70, 708–713; (b) Vale, J.; Fernández-Pereira, C.; Alcalde, M. J. Chem. Educ. 1993, 70, 790–795; (c) Fernández-Pereira, C.; Vale, J. Chem. Educator 1996, 6, 1–18; (d) Fernández-Pereira, C.; Vale, J.; Alcalde, M. Chem. Educator 2003, 8, 15–21; (e) Fernández-Pereira, C.; Alcalde, M.; Villegas, R.; Vale, J. J. Chem. Educ. 2007, 84, 520–525.
3. See, for example, (a) Bower, V. E.; Bates, R. G. J. Res. Natl. Bur. Stand. (U. S.) 1955, 55, 197–200; (b) Bates, R. G. Ann. N. Y. Acad. Sci. 1961, 92, 341–356; (c) Bates, R. G. Determination of pH, 2nd ed.; Wiley-Interscience: New York, 1973.
4. (a) Lambert, W. J. J. Chem. Educ. 1990, 67, 150–153; (b) http://www.bioinformatics.org/JaMBW/5/4/index.html.
5. Lister, M. W.; Rivington, D. E. Can. J. Chem. 1995, 33, 1572–1590.
6. Davies, C. W. Ion Association, Butterworth: London, 1962.

Contributors and Attributions

David Harvey (DePauw University)