14: Linear combination of atomic orbitals

Linear combination of atomic orbitals (LCAO) is a simple method of quantum chemistry that yields a qualitative picture of the molecular orbitals (MOs) in a molecule. Let us consider \(H_{2}^{+}\) again. The approximation embodied in the LCAO approach is based on the notion that when the two protons are very far apart, the electron in its ground state will be a \(1s\) orbital of one of the protons. Of course, we do not know which one, so we end up with a Schrödinger cat-like state in which it has some probability to be on one or the other.

As with the HF method, we propose a guess of the true wave function for the electron

\[\psi_g (r)=C_{A} \psi_{1s}^{A}(r)+C_B \psi_{1s}^{B}(r)\]

where \(\psi_{1s}^{A}(r)=\psi_{1s}(r-R_A)\) is a \(1s\) hydrogen orbital centered on proton A and \(\psi_{1s}^{B}(r)=\psi_{1s}(r-R_B)\) is a \(1s\) hydrogen orbital centered on proton B. Recall \(\psi_{1s}(r)=\psi_{100}(r,\phi ,\theta)\). The positions \(R_A\) and \(R_B\) are given simply by the vectors

\[R_A =(0,0,R/2)\;\;\;\;R_B =(0,0,-R/2)\]

The explicit forms of \(\psi_{1s}^{A}(r)\) and \(\psi_{1s}^{B}(r)\) are

\[\begin{align*}\psi_{1s}^{A}(r) &= \frac{1}{(\pi a_{0}^{3})^{1/2}}e^{-|r-R_A|/a_0}\\ \psi_{1s}^{B}(r) &= \frac{1}{(\pi a_{0}^{3})^{1/2}}e^{-|r-R_B|/a_0}\end{align*}\]

Now, unlike the HF approach, in which we try to optimize the shape of the orbitals themselves, in the LCAO approach, the shape of the \(\psi_{1s}\) orbital is already given. What we try to optimize here are the coefficients \(C_A\) and \(C_B\) that determine the amplitude for the electron to be found on proton A or proton B.

The guess wave function \(\psi_g (r)\) is not normalized as we have written down. Thus, our guess of the ground-state energy is given by

\[E_g =\frac{\int \psi_g \hat{H}_{elec} \psi_g dV}{\int \psi_{g}^{2}dV}\]

where \(dV\) is the electron's volume element, and \(\hat{H}_{elec}\) is the electronic Hamiltonian (minus the nuclear-nuclear repulsion \(ke^2 /R\):

\[\hat{H}_{elec}=\hat{K}_e -ke^2\left ( \frac{1}{|r-R_A|}+\frac{1}{|r-R_B|} \right )\]

(we will account for the nuclear-nuclear repulsion later when we consider the energies). Consider the denominator first:

\[\int \psi_{g}^{2}dV=C_{A}^{2}\int \psi_{1s}^{2}(r-R_A)dV +C_{B}^{2}\int \psi_{1s}^{2}(r-r_B)dV+2C_A C_B \int \psi_{1s}(r-R_A)\psi_{1s}(r-R_B)dV\]

Now, the \(1s\) wave function of hydrogen is normalized so

\[\int\psi_{1s}^{2}(r-R_A)=\int \psi_{1s}^{2}(r-R_B)=1\]

In the cross term, however, the integral

\[\int \psi_{1s}(r-R_A)\psi_{1s}(r-R_B)dV\]

is not 1 because the orbitals are centered on different protons (it is only one if the two protons sit right on top of each other, which is not possible). It is also not 0 unless the protons are very far apart. We can calculate the integral analytically, however, it is not that important to do so since there is no dependence on \(C_A\) or \(C_B\). Let us just denote this integral as \(S\). We know that \(0 \leq S\leq 1\) and this is good enough for now. Thus, the denominator is simply

\[\int \psi_{g}^{2}dV=C_{A}^{2}+C_{B}^{2}+2SC_A C_B\]

As for the numerator

\[\int \psi_g \hat{H}_{elec}\psi_g dV=C_{A}^{2}H_{AA}+C_{B}^{2}H_{BB}+2C_A C_B H_{AB}\]

where we have defined a bunch of integrals I'm too lazy to do as

\[\begin{align*}H_{AA} &=\int \psi_{1s}^{A}(r)\hat{H}_{elec}\psi_{1s}^{A}(r)dV\\ H_{BB} &=\int \psi_{1s}^{B}(r)\hat{H}_{elec}\psi_{1s}^{B}(r)dV\\ H_{AB} &= \int \psi_{1s}^{A}(r)\hat{H}_{elec}\psi_{1s}^{B}(r)dV\end{align*}\]

Again, these are integrals we can do, but it is not that important, so we will just keep the shorthand notation. Note that since the two nuclei are the same (they are both protons), we expect \(H_{AA}=H_{BB}\). Since these are equal, we will just call them both \(H_{AA}\). Hence, the guess energy becomes

\[E_g =\frac{H_{AA}(C_{A}^{2}+C_{B}^{2})+2H_{AB}C_A C_B}{C_{A}^{2}+C_{B}^{2}+2SC_A C_B}\]

which is just a ratio of two simple polynomials. Since we know that \(E_g >E_0\), where \(E_0\) is the true ground-state energy, we can minimize \(E_g\) with respect to the two coefficients \(C_A\) and \(C_B\). Thus, we need to take two derivatives and set them both to 0:

\[\frac{dE_g}{dC_A}=0 \;\;\;\; \frac{dE_g}{dC_B}=0\]

Defining the denominator simply as \(D\), where \(D=C_{A}^{2}+C_{B}^{2}+2SC_A C_B\), the two derivatives are

\[\begin{align*}\frac{dE_g}{dC_A} &= \frac{2C_A H_{AA}+2C_B H_{AB}}{D}-\frac{H_{AA}(C_{A}^{2}+C_{B}^{2})+2C_A C_B H_{AB}}{D^2}(2C_A +2SC_B)=0\\ \frac{dE_g}{dC_B} &= \frac{2C_B H_{AA}+2C_A H_{AB}}{D}-\frac{H_{AA}(C_{A}^{2}+C_{B}^{2})+2C_A C_B H_{AB}}{D^2}(2C_B +2SC_A)=0\end{align*}\]

Thus, we have two algebraic equations in two unknowns \(C_A\) and \(C_B\). In fact, these will not determine \(C_A\) and \(C_B\) uniquely because they are redundant. However, we also have the normalization of \(\psi_g\) as a third condition, so we have enough information to determine the coefficients absolutely.

The equations can be solved as follows: First we write them as

\[\begin{align*}\frac{2C_A H_{AA}+2C_B H_{AB}}{D} &=\frac{H_{AA}(C_{A}^{2}+C_{B}^{2})+2C_A C_B H_{AB}}{D^2}(2C_A +2SC_B)\\ \frac{2C_B H_{AA}+2C_A H_{AB}}{D} &= \frac{H_{AA}(C_{A}^{2}+C_{B}^{2})+2C_A C_B H_{AB}}{D^2}(2C_B 2SC_A)\end{align*}\]

We now divide one equation by the other, which yields

\[\frac{C_A H_{AA}+C_B H_{AB}}{C_B H_{AA}+2C_A H_{AB}}=\frac{C_A +SC_B}{C_B + SC_A}\]

Since we cannot solve for \(C_A\) and \(C_B\) independently, we choose, instead, to solve for the ratio \(r=C_A /C_B\). Dividing both sides of the above by equation by \(C_B\) yields

\[\frac{rH_{AA}+H_{AB}}{H_{AA}+rH_{AB}}=\frac{r+S}{1+rS}\]

To solve for \(r\), we cross multiply:

\[(rH_{AA}+H_{AB})(1+rS)=(H_{AA}+rH_{AB})(r+S)\]

Multiplying this out, we obtain

\[\begin{align*}rH_{AA}+r^2 SH_{AA}+H_{AB}+rSH_{AB} &= rH_{AA}+r^2 H_{AB}+SH_{AA}+rSH_{AB}\\ r^2(SH_{AA}-H_{AB}) &= SH_{AA}-H_{AB}\\r^2 &=1\end{align*}\]

which implies \(r=\pm 1\).

Thus, we have two solutions: \(C_A =C_B\) or \(C_A =-C_B\). So, to simplify the notation, Let \(C_A =C\) (drop the A subscript). We, therefore, have two possible guess wave functions:

\[\begin{align*}\psi_+ (r) &= C[\psi_{1s}^{A}(r)+\psi_{1s}^{B}(r)]\\ \psi_- (r) &= C[\psi_{1s}^{A}(r)-\psi_{1s}^{B}(r)]\end{align*}\]

The constant \(C\) can be determined for each guess wave function by imposing the normalization condition. For \(\psi_+\), we have

\[\begin{align*} \int \psi_{+}^{2}(r)dV &= C^2 \left [ \int \psi_{1s}^{2}(r-R_A)dV+\int \psi_{1s}^{2}(r-R_B)dV+2\psi_{1s}(r-R_A)\psi_{1s}(r-R_B)dV \right ] =1\\ & C^2[1+1+2S]=1\\ & C=\frac{1}{\sqrt{2(1+S)}}\end{align*}\]

Similarly, one can show that for \(\psi_-\), \(C=1\sqrt{2(1-S)}\).

Let us now see how the two approximate solutions lead to bonding and antibonding orbitals. Consider first \(\psi_+ (r)\). We will add these two wave functions pictorally, keeping in mind that \(\psi_{1s}\) is a spherically symmetric orbital with an exponential decay. Thus,

\[\begin{align*}\psi_{1s}^{A}(r) &\propto e^{-|r-R_A|/a_0}\\ \psi_{1s}^{B}(r) &\propto e^{-|r-R_B|/a_0}\end{align*}\]

The figure below shows the orbitals that result from the addition or subtraction for \(\psi_+\) or \(\psi_-\).

Figure: LCAO approximation to the ground \((1\sigma_g)\) and first excited \((1\sigma_{u}^{*})\) orbitals in \(H_{2}^{+}\).

In the bottom left panel, we show the two \(1s\) orbitals centered on protons A and B in \(\psi_+\). In the center on the left, the result of adding them together is shown. It should be clear from the figure that \(\psi_+\) is a bonding orbital that is an approximation to the true \(1\sigma_g\) orbital that is the true ground state. This approximation is often denoted \(\sigma_{g1s}\). On the other hand, the orbital \(\psi_-\) is the difference between \(\psi_{1s}(r-r_A)\) and \(\psi_{1s}(r-r_B)\), which is depicted in the top left panel. This orbital has a node between the two nuclei and the amplitude between the two nuclei is generally low. This is clearly an anti-bonding orbital corresponding to \(1\sigma_{u}^{*}\). This approximate orbital is often denoted \(\sigma_{u1s}^{*}\). Since this orbital has a node, we expect that its energy will be higher than the approximate ground-state energy \(\sigma_{g1s}\).

Concerning the energies, the figure below shows the two lowest energies curves as functions of \(R\), comparing the results from the exact solution for \(H_{2}^{+}\) and the LCAO approximation. Note, in particular, that, in accordance with the variational principle, the exact energy curve for the ground state is always lower than the LCAO approximation.

Energies in the LCAO method

The LCAO approach for \(H_{2}^{+}\) yields two wave functions we called \(\psi_+ (r)\) and \(\psi_- (r)\). The corresponding energies are

\[E_+ (R)=\frac{H_{AA}(R)+H_{AB}(R)}{1+S(R)}+\frac{ke^2}{R}\;\;\;\;E_- (R)=\frac{H_{AA}(R)-H_{AB}(R)}{1-S(R)}+\frac{ke^2}{R}\]

where \(E_+ (R)<E_- (R)\), and we have indicated the explicit dependence of \(H_{AA}\), \(H_{AB}\), and \(S\) on the internuclear distance \(R\). Do not for get that both of these energies depend on the internuclear separation \(R\). The figure below shows the two energies (adjusted to go to zero as \(R \rightarrow \infty\)) as a function of \(\rho =R/a_0\):

As with the exact treatment, we see that the surface \(E_+\) (or \(\Delta E_+\) in the figure) has a minimum at the equilibrium bond length, which is consistent with the fact that \(\psi_+ (r)\) is a bonding orbital. \(E_-\) (or \(\Delta E_-\) in the figure) has no such minimum and decreases monotonically, consistent with the fact that \(\psi_- (r)\) is an antibonding orbital. Since \(\psi_+ (r)\) is an approximation to the true \(1\sigma_g\) orbital, we will use the notation \(\sigma_{g1s}\) for this orbital. Here, the "g" designator indicates that it is an even function, while the \(1s\) tells us that it is generated from a linear combination of \(1s\) orbitals. Similarly, the orbital \(\psi_- (r)\) is denoted \(\sigma_{u1s}^{*}\), where the asterisk indicates antibonding character, and the "u" designator tells us that it is an odd function.

The following figure shows LCAO energies compare to the energies obtained by solving the Schrödinger equation exactly:

Quantitatively, the LCAO predicts a bond length of \(1.32 \ \stackrel{\circ}{A}\) while experiment and the exact solution give \(1.06 \ \stackrel{\circ}{A}\). The dissociation energy \(\Delta E_d\) (also denoted \(D_e\)) from LCAO is \(1.76 \ eV=0.13 \ Ry\), while the exact value is 2.791 eV = \(2.791 \ eV=0.21 \ eV\). This level of agreement is less than wonderful, but at the very least, LCAO gives us a correct qualitative picture that is useful for rationalizing chemical bonding situations.

The \(\sigma_{g1s}\) orbital is lower in energy than the \(\sigma_{u1s}^{*}\). We can show this on an energy level diagram as well as the placement of the electron into the appropriate orbital for \(H_{2}^{+}\). Such a diagram is called a correlation diagram. For \(H_{2}^{+}\), the diagram appears as shown below:

Figure 2: \(H_{2}^{+}\) correlation diagram.

The diagram shows the two atomic orbitals (AOs) that were used to generate the corresponding MOs. These are both \(1s\) orbitals, so these are shown at the extremes of the diagram as well as the electronic configurations of each atom. Here, just one electron occupies a single \(1s\) orbital. The two MOs generated from the two AOs are also shown. Note that the \(\sigma_{g1s}\) orbital has a lower energy than the \(1s\) orbital because it has a minimum and leads to a stable bond (\(1s\), by contrast, is monotonically decreasing). That the \(\sigma_{g1s}\) orbital is lower in energy can also be proved by comparing its energy \((H_{AA}+H_{AB})/(1+S)\) to the energy of the \(1s\) orbital of hydrogen. Similarly, the orbital \(\sigma_{u1s}^{*}\) is shown as having a higher energy because of its antibonding or destabilizing effect. That is has a higher energy than 1s of hydrogen can also be seen by comparing its energy \((H_{AA}-H_{AB})/(1-S)\) to the energy of a \(1s\) orbital of hydrogen. In \(H_{2}^{+}\), the electron in the \(1s\) orbital occupies the \(\sigma_{g1s}\) MO, which is also shown in the diagram.

LCAO and the aufbau principle for molecules

The ``aufbau'' concept applied to the MOs produced from LCAO follows the same rules as for atoms. That is, we have to obey the Pauli exclusion principle and apply Hund's rule. Thus, for the molecule \(H_2\), we have two electrons: Each \(H_2\) donates one in a \(1s\) orbital to the LCAO procedure. We already know that combining two \(1s\) orbitals gives us the \(\sigma_{g1s}\) and \(\sigma_{u1s}^{*}\) MOs, and since they are different in energy, we do not need to worry about Hund's rule. We simply place both electrons (in opposite spin configurations) into the \(\sigma_{g1s}\) orbital as the correlation diagram below illustrates:

Figure 3: \(H_2\) correlation diagram

For the molecule \(He_{2}^{+}\), we have three electrons. On one of the \(He\) atoms, there are two electrons both in a \(1s\) orbital, while on the \(He^+\) atom, there will be one electron in a \(1s\) orbital. Note, however, that these \(1s\) orbitals are only hydrogen-like but have a \(Z\) value of \(Z=2\). That is, the \(1s\) orbital is

\[\psi_{100}(r, \phi ,\theta)=\left ( \frac{8}{\pi a_{0}^{3}} \right )^{1/2}e^{-2r/a_0}\]

Hence, if the He nuclei are at positions \(r_A\) and \(r_B\), the guess wave function for the LCAO procedure would take the form

\[\psi_g (r)=C_A \psi_{1s(Z=2)}(r-r_A)+C_B \psi_{1s(Z=2)}(r-r_B)\]

The procedure would still yield \(\psi_+ (r)\) and \(\psi_- (r)\) orbitals, but these would also use \(Z=2\) rather than \(Z=1\) in their construction. Now, since only two electrons can occupy the \(\psi_+ (r)\) or \(\sigma_{g1s}\) orbital that LCAO gives, the third electron must be placed in the \(\psi_- (r)\) or \(\sigma_{u1s}^{*}\) orbital. This gives a correlation diagram that appears as shown below:

Figure 4: \(He_{2}^{+}\) correlation diagram

The fact that an electron must be placed in an antibonding orbitals means that there will be some destabilization of the bond, and indeed, we find that \(He_{2}^{+}\) is more weakly bonded than \(H_2\). Moreover, the bonding orbital \(\sigma_{g2s}\) has less electron density between the two nuclei because the decay of the \(1s(Z=2)\) wave function is faster than that of the \(1s(Z=1)\) wave function used to construct the MOs for \(H_{2}^{+}\) and \(H_2\). In order to give a sense of this, consider that the bond lengths of \(H_{2}^{+}\) and \(He_{2}^{+}\) are \(1.06 \ \stackrel{\circ}{A}\) and \(1.08 \ \stackrel{\circ}{A}\), which are very similar, yet the dissociation energies of these two molecules are \(276 \ kJ/mol\) and \(230 \ kJ/mol\), so \(He_{2}^{+}\) is more weakly bound that \(H_{2}^{+}\). By comparison, \(H_2\), which has two bonding electrons has a bond length of \(0.74 \ \stackrel{\circ}{A}\), and a dissociation energy of \(432 \ kJ/mol\).

For the helium dimer \(He_2\), there are four electrons, each He atom contributing 2 electrons in \(1s\) orbitals. When placing these electrons into the \(\sigma_{g1s}\) and \(\sigma_{u1s}^{*}\) MOs, we are forced to place two electrons into each, which means two electrons in the bonding orbital and two in the antibonding orbital. LCAO predicts that two electrons in an antibonding orbital generates as much destabilization of the bond as there is stabilization from the two bonding electrons. Thus, LCAO would predict that \(He_2\) cannot form a stable bond. In fact, a very weak bond stabilization of roughly \(10^{-8} \ Ry\) exists between to helium atoms, resulting in a very weak \(He_2\) dimer with a bond length of approximately \(52 \ \stackrel{\circ}{A}\)! (see Grisenti et al. Phys. Rev. Lett. 85, 2284 (2000)). Of course, LCAO cannot predict this. Nevertheless, LCAO gives us an easy way to estimate the stability of a chemical bond which is qualitatively reasonable (even if it misses exotic objects like the weak \(He_2\) dimer). Within LCAO, we can define a bond order

\[Bond \ order=\frac{1}{2}[\# electrons \ in \ bonding \ orbitals-\#electrons \ in \ antibonding \ orbitals]\]

Applying this formula, we can obtain bond orders for the molecules we have considered thus far:

\[\begin{align*}For \ H_{2}^{+}: \ Bond \ order &= \frac{1}{2}[1-0]=\frac{1}{2}\\ For \ H_2 : \ Bond \ order &= \frac{1}{2}[2-0]=1\\ For \ He_{2}^{+}: \ Bond \ order &= \frac{1}{2}[2-1]=\frac{1}{2}\\ For \ He_{2}: \ Bond \ Order &= \frac{1}{2}[2-2]=0\end{align*}\]

As expected, the weaker bonds have lower bond orders.

The electronic configurations of \(H_{2}^{+}\), \(H_2\) and \(He_{2}^{+}\) are written in an manner analogous to the atomic case:

\[\begin{align*}For \ H_{2}^{+} &: (\sigma_{g1s})^1\\ For \ H_2 &: (\sigma_{g1s})^2\\ For \ He_{2}^{+} &: (\sigma_{g1s})^2(\sigma_{u1s}^{*})^1\end{align*}\]

At this point, we state the general rules for constructing MOs from AOs in the LCAO procedure:

1. Form linear combinations of the minimum number of AOs to generate MOs. The number of MOs must equal the number of AOs from which they are generated.
2. Arrange the MOs in order from lowest to highest in energy.
3. Occupy or place electrons in MOs starting from MOs of lowest energy following the Pauli exclusion principle (at most 2 electrons per MO) and Hund's rule for MOs of similar energy.

Contrasting LCAO with other quantum chemistry methods

Before we move onto atoms in the second period of the periodic table, let us pause briefly to contrast the LCAO approach with other methods of quantum chemistry. As we have already seen, the LCAO approach is very approximate, yielding only qualitative results.

It should be noted that the Hartree-Fock method we introduced in Chapter 5 can also be used for molecules. For example, the molecule \(He_{2}^{+}\) has three electrons, and the Li atom also has three electrons. Thus, the guess wave function that you wrote down for the \(Li\) atom in the last problem set can also be used as a guess wave function for \(He_{2}^{+}\)! As usual with Hartree-Fock, the idea is to optimize the shapes of the single-electron orbitals \(\psi_1 (r)\), \(\psi_2 (r)\) and \(\psi_3 (r)\) by minimizing the guess to the ground state energy \(E_g\). Of course, we will not get the same answer as for \(Li\) because there is a different \(V_{en}\) energy for \(He_{2}^{+}\) due to the presence of two positively charge nuclei \((charge=+2e)\) separated by a distance \(R\) in contrast to the single \(+3e\) charged nucleus for \(Li\). When the shapes of the orbitals are optimized, we also obtain three energy \(\varepsilon_1\), \(\varepsilon_2\) and \(\varepsilon_3\). Not unexpectedly, we find that two of the HF orbitals resemble \(1\sigma_g\) while the third resembles \(1\sigma_{u}^{*}\) and the first two energies \(\varepsilon_1\) and \(\varepsilon_2\) will be nearly equal, while the third \(\varepsilon_3\) will be noticeably higher. To contrast with the LCAO approach, in LCAO, we do not optimize the shapes of the orbitals (these are assumed a priori to be \(1s\) shaped). All we do is choose the mixing coefficients so as to minimize the guess to the ground-state energy \(E_g\).

We note, finally, that the density functional theory alluded to earlier can also be used for molecules. It is often the case that density functional theory yields a more accurate description than Hartree-Fock, but this depends on the molecule. In any case, both are more accurate than LCAO. There is also a hierarchy of methods called post Hartree-Fock methods, all of which are based on the wave function rather than the electron density, that can be used to improve upon the HF approximation systematically. The greater the accuracy that is desired for the calculation, the more costly computationally the post HF methods become, so quantum chemistry is often a trade-off between accuracy and efficiency, an issue that becomes more critical to take into account when calculations on large molecules must be carried out!

LCAO for second-period atoms in homonuclear diatomic molecules

A homonuclear diatmoic is of the form XX, i.e. the two nuclei are the same. In this section we will consider homonuclear diatomics formed from the second period (\(Z=3\) through \(Z=10\)) atoms.

In the LCAO approach, the most general guess wave function we could imagine constructing would be a general linear combination including \(1s\), \(2s\), and \(2p\) orbitals on nuclei A and B. Fortunately, we do not need to make things so complex due to a few simple rules that we can easily understand from the quantum mechanical concepts we have developed so far.

Let us briefly consider \(H_{2}^{+}\) again and the \(\sigma_{g1s}\) orbital, which takes the form

\[\psi_+ (r)=\psi_{\sigma_{g1s}}(r)=\frac{1}{\sqrt{2(1+S)}}[\psi_{1s}(r-r_A)+\psi_{1s}(r-r_B)]\]

Note that this is a Schrödinger cat type of state in which the electron is simultaneously in a \(1s\) orbital on nucleus A and in a \(1s\) orbital on nucleus B, and this remains the case unless somebody comes alongs and measures the position of the electron! Let us suppose, for simplicity, that the nuclei are far enough apart that we can safely set \(S=0\) (recall that \(S\) is the integral of the product of \(\psi_{1s}(r-r_A)\psi_{1s}(r-r_B)\). Then, \(\psi_+ (r)\) becomes

\[\psi_+ (r)\approx \frac{1}{\sqrt{2}}[\psi_{1s}(r-r_A)+\psi_{1s}(r-r_B)]\]

When written in this approximation, we easily see that the probability of finding the electron in the \(1s\) orbital of atom A is \(1/2\), and the probability of finding the electron in the \(1s\) orbital of atom B is \(1/2\). This makes physical sense because both \(1s\) orbitals have the same energy.

Now suppose we try a guess wave function that mixes \(1s\) and \(2s\) orbitals, e.g.

\[\psi_g (r)=C_A \psi_{1s}(r-r_A)+C_B \psi_{2s}(r-r_B)\]

The \(1s\) and \(2s\) orbitals have very different energies. Thus, while we might be able to prepare a state like this under special laboratory conditions, a molecule in its equilibrium state would be very unlikely to be in a state of this character because of the disparity in energies. We would, therefore, expect that the probabilities for finding the electron in the \(1s\) and \(2s\) states would behave like \(|C_A|^2 \gg |C_B|^2\) rather than \(|C_A|^2=|C_B|^2\), as is the case when the energies are equal. Without significant amplitude from the \(\psi_{2s}\)orbital, we cannot expect a bond to form. So, unless the contributions from atom A and atom B are nearly equal, no bonding occurs.

Based on this consideration, we can state the following rule:

1. Two AOs contribute significantly to bond formation only if their atomic energy levels are close to one another.

Another important rule is one to which we have already alluded:

2. Two AOs contribute signifcantly to bond formation only if they overlap significantly. This means that they must combine in such a way as to have substantial overlap in the region between the two nuclei.

A rule such as this means that we do not need to consider the mixing of \(2p_x\) and \(2p_y\) orbitals, for example. These two rules greatly simplifies the construction of MOs within the LCAO scheme. A mixture of \(2p_x\) and \(2p_y\) orbitals have neither bonding nor antibonding character, and they do not resemble either exact solutions for \(H_{2}^{+}\) nor do they resemble any of the HF orbitals for other diatomics.

The MOs we can create, following the pattern for \(\psi_{\sigma_{g1s}}\) and \(\psi_{\sigma_{u1s}^{*}}\) start with the MO generated from \(2s\) AOs:

\[\begin{align*}\psi_{\sigma_{g2s}} &= \frac{1}{\sqrt{2(1+S)}}[\psi_{2s}(r-r_A)+\psi_{2s}(r-r_B)]\\ \psi_{\sigma_{u2s}^{*}}(r)&=\frac{1}{\sqrt{2(1-S)}}[\psi_{2s}(r-r_A)-\psi_{2s}(r-r_B)]\end{align*}\]

Note that the definition of \(S\) is a different here. It is the overlap between the \(2s\) orbitals

\[S= \int \psi_{2s}(r-r_A)\psi_{2s}(r-r_B)dV\]
For the \(2p\) orbitals, we can generate MOs of \(\sigma\) character by combining the \(2p_z\) orbitals, for which the \(L_z\) quantum number \(m=0\). Consider first the orbital

\[\frac{1}{\sqrt{2(1-S)}}[\psi_{2p_z}(r-r_A)-\psi_{2p_z}(r-r_B)]\]

Because the \(p_z\) orbital peaks on the z-axis and is positive along the positive z-axis and negative along the negative z-axis, the difference enhances the amplitude in the region between the nuclei (see figure below - top panel):

Figure 5: MOs generated from \(2p_z\) AOs using the LCAO scheme

This orbital is clearly a bonding orbital and is an even function. Hence we denote at as a \(\sigma_{g2p_z}\) orbital and write:

\[\psi_{\sigma_{g2p_z}}(r)=\frac{1}{\sqrt{2(1-S)}}[\psi_{2p_z}(r-r_A)-\psi_{2p_z}(r-r_B)]\]

Here, the definition of \(S\) is:

\[S=\int \psi_{2p_z}(r-r_A)\psi_{2p_z}(r-r_B)dV\]

and clearly

\[\psi_{\sigma_{g2p_z}}(-r)=\psi_{\sigma_{g2p_z}}(r)\]

The other construction

\[\frac{1}{\sqrt{2(1+S)}}[\psi_{2p_z}(r-r_A)+\psi_{2p_z}(r-r_B)]\]

has very little amplitude in the region between the nuclei because the negative lobe of one of the \(2p_z\) orbitals cancels the positive lobe of the other (see the figure above - bottom panel). This orbital is, therefore, an antibonding orbital that is odd. We, therefore, designate it as a \(\sigma_{u2p_z}^{*}\) orbital and write

\[\psi_{\sigma_{u2p_z}^{*}}(r)=\frac{1}{\sqrt{2(1+S)}}[\psi_{2p_z}(r-r_A)+\psi_{2p_z}(r-r_B)]\]
For the \(2p_x\) orbitals, consider the combination

\[\frac{1}{\sqrt{2(1+S)}}[\psi_{2p_x}(r-r_A)+\psi_{2p_x}(r-r_B)]\]

This combination is pictured in the top panel of the figure below:

Figure 6: MOs generated from \(2p_x\) AOs using the LCAO scheme

This turns out to be a bonding orbital because there is significant amplitude between the nuclei, however, the orbital is an odd function. So, we have to designate it as \(\pi_{u2p_x}\). Note that it is a \(\pi\) orbital because \(m=\pm 1\). Thus, we have

\[\psi_{\pi_{u2p_x}}(r)=\frac{1}{\sqrt{2(1+S)}}[\psi_{2p_x}(r-r_A)+\psi_{2p_x}(r-r_B)]\]

The different orbital becomes an antibonding orbital (see above figure - bottom panel) that happens to be an even function and is, therefore, a \(\pi_{g2p_x}^{*}\) orbital:

\[\psi_{\pi_{g2p_x}^{*}}(r)=\frac{1}{\sqrt{2(1-S)}}[\psi_{2p_x}(r-r_A)-\psi_{2p_x}(r-r_B)]\]

The same applies to the MOs constructed from \(2p_y\) AOs.

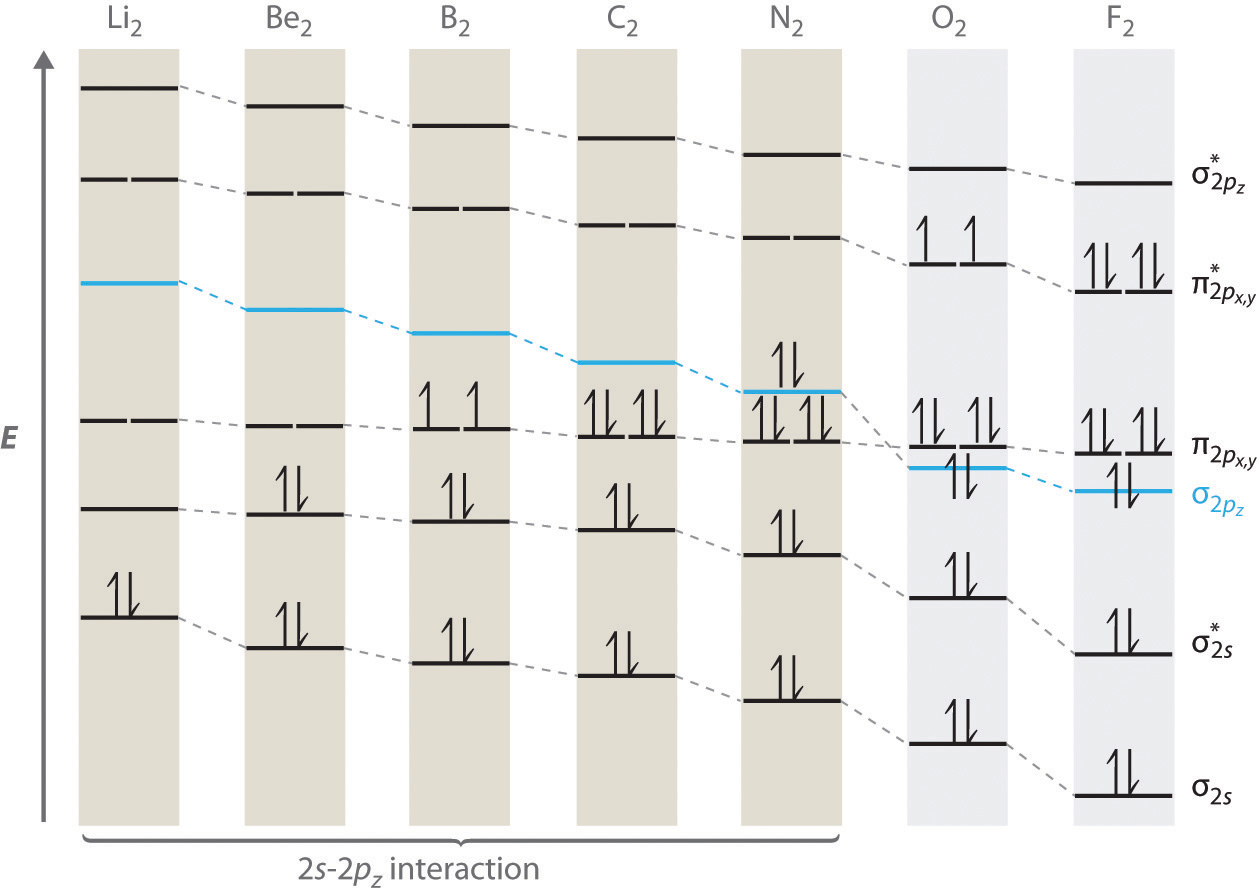
The energetic ordering of these orbitals is \(\sigma_{g2s}\), \(\sigma_{u2s}^{*}\), \((\pi_{u2p_x},\pi_{u2p_y})\) (these two \(\pi\) orbitals have the same energy), \(\sigma_{g2p_z}\), \((\pi_{g2p_x}^{*},\pi_{g2p_y}^{*})\), \(\sigma_{u2p_z}^{*}\) for atoms \(Li\) through \(N\). For \(O\), \(F\) and \(Ne\), the ordering is \(\sigma_{g2s}\), \(\sigma_{u2s}^{*}\), \(\sigma_{g2p_z}\), \((\pi_{u2p_x},\pi_{u2p_y})\) (these two \(\pi\) orbitals have the same energy), \((\pi_{g2p_x}^{*},\pi_{g2p_y}^{*})\), \(\sigma_{u2p_z}^{*}\). The reason for this difference between the \(Z \leq 5\) and \(Z \geq 6\) elements can be understood roughly as follows: The \(\sigma_{g2p_z}\) orbital has considerable electron density along the z-axis. For \(Z \leq 5\), the contributing \(2p_z\) orbitals are sufficiently delocalized along this axis that electrons occupying them overlap and, therefore, contribute significant Coulomb repulsion to the total energy, which raises the energy of the \(\sigma_{g2p_z}\) orbital above the orbitals, for which the Coulomb repulsion is considerably less, as they do not peak along the z-axis. For \(Z \geq 6\), however, the nuclear charge is sufficiently high that the \(2p_z\) orbitals decay more quickly, are more localized, and this reduces the overlap and Coulomb repulsion to such an extent that the energy of the \(\sigma_{g2p_z}\) orbital is now below that of the \(\pi\) orbitals. Only high level calculations could predict that this change occurs between \(Z=5\) and \(Z=6\). Note that, generally, as the number of nodes in the wave function increases, so does the energy. The ordering and shapes of the orbitals are shown in the figure below, together with some example correlation diagrams for \(N_2\) and \(F_2\):

\[\frac{1}{\sqrt{2(1+S)}}[\psi_{2p_x}(r-r_A)+\psi_{2p_x}(r-r_B)]\]

This combination is pictured in the top panel of the figure below:

Figure 7: MOs and their ordering

Following Pauli's exclusion principle and Hund's rule, the electronic configurations for the second-period diatomics are shown in the figure below:

Note the special cases of \(B_2\) and \(O_2\), both of which contains unpaired spins because of Hund's rule. Because of these unpaired spins, these molecules interact strongly with a magnetic field and can be made to align with such a field. For this reason, these molecules are called paramagnetic. This type of behavior can only be predicted within quantum mechanics. The classical theory of chemical bonding from Chapter 3 misses this entirely. The paramagnetic behavior of \(O_2\) means that liquid oxygen pored between the poles of a magnet will not flow through but will stick to the poles due to the ability of spins to align with a magnetic field and the forces exerted by the magnet on these spins. This is illustrated in the figure below:

Contributors and Attributions

• Mark Tuckerman (New York University)