8.5: Mixtures of Gases
- Page ID
- 96305
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- To determine the contribution of each component gas to the total pressure of a mixture of gases
In our use of the ideal gas law thus far, we have focused entirely on the properties of pure gases with only a single chemical species. But what happens when two or more gases are mixed? In this section, we describe how to determine the contribution of each gas present to the total pressure of the mixture.
Partial Pressures
The ideal gas law assumes that all gases behave identically and that their behavior is independent of attractive and repulsive forces. If volume and temperature are held constant, the ideal gas equation can be rearranged to show that the pressure of a sample of gas is directly proportional to the number of moles of gas present:
\[P=n \bigg(\dfrac{RT}{V}\bigg) = n \times \rm const. \label{6.6.1}\]
Nothing in the equation depends on the nature of the gas—only the amount.
With this assumption, let’s suppose we have a mixture of two ideal gases that are present in equal amounts. What is the total pressure of the mixture? Because the pressure depends on only the total number of particles of gas present, the total pressure of the mixture will simply be twice the pressure of either component. More generally, the total pressure exerted by a mixture of gases at a given temperature and volume is the sum of the pressures exerted by each gas alone. Furthermore, if we know the volume, the temperature, and the number of moles of each gas in a mixture, then we can calculate the pressure exerted by each gas individually, which is its partial pressure, the pressure the gas would exert if it were the only one present (at the same temperature and volume).
To summarize, the total pressure exerted by a mixture of gases is the sum of the partial pressures of component gases. This law was first discovered by John Dalton, the father of the atomic theory of matter. It is now known as Dalton’s law of partial pressures. We can write it mathematically as
\[P_{tot}= P_1+P_2+P_3+P_4 \; ... = \sum_{i=1}^n{P_i} \label{6.6.2}\]
where \(P_{tot}\) is the total pressure and the other terms are the partial pressures of the individual gases (up to \(n\) component gases).
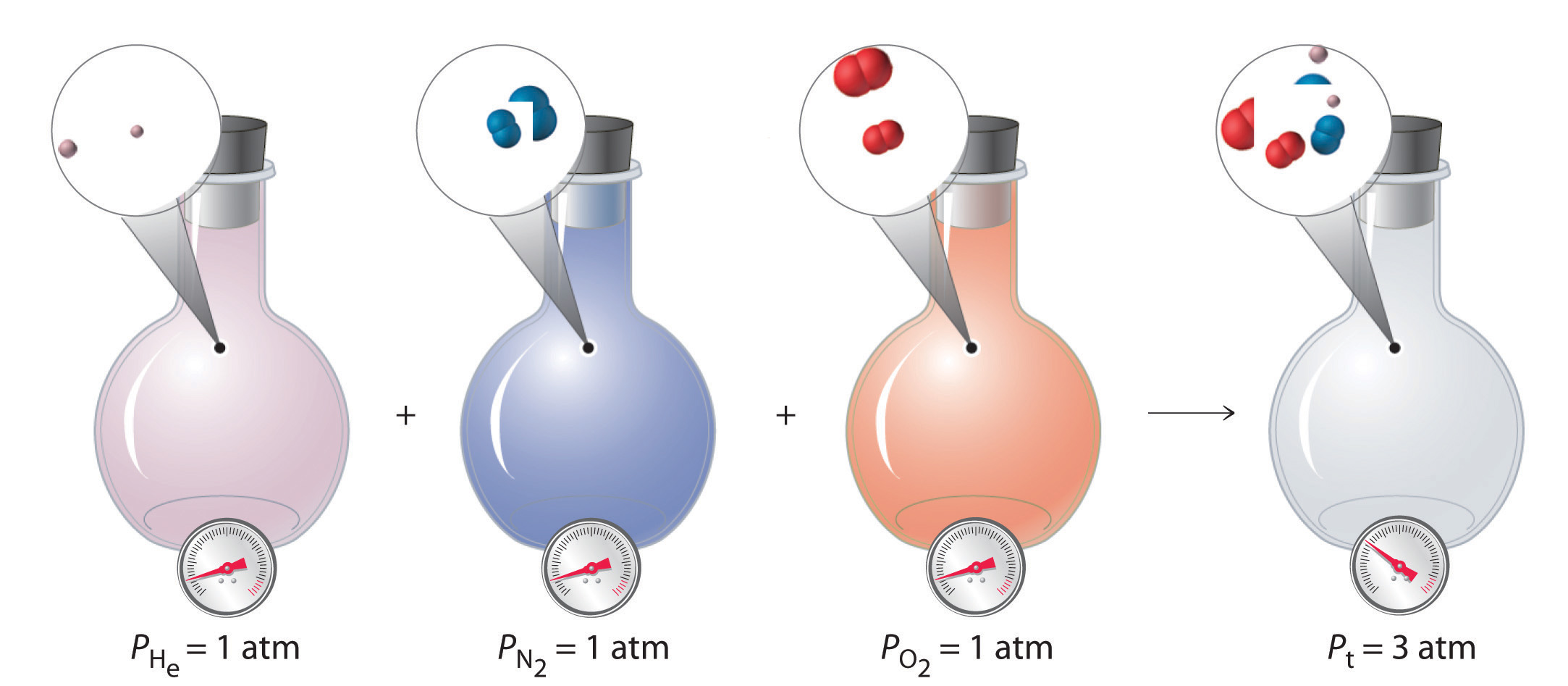
For a mixture of two ideal gases, \(A\) and \(B\), we can write an expression for the total pressure:
\[P_{tot}=P_A+P_B=n_A\bigg(\dfrac{RT}{V}\bigg) + n_B\bigg(\dfrac{RT}{V}\bigg)=(n_A+n_B)\bigg(\dfrac{RT}{V}\bigg) \label{6.6.3}\]
More generally, for a mixture of \(n\) component gases, the total pressure is given by
\[P_{tot}=(P_1+P_2+P_3+ \; \cdots +P_n)\bigg(\dfrac{RT}{V}\bigg)\label{6.6.2a}\]
\[P_{tot}=\sum_{i=1}^n{n_i}\bigg(\dfrac{RT}{V}\bigg)\label{6.6.2b}\]
Equation 6.6.4 restates Equation 6.6.3 in a more general form and makes it explicitly clear that, at constant temperature and volume, the pressure exerted by a gas depends on only the total number of moles of gas present, whether the gas is a single chemical species or a mixture of dozens or even hundreds of gaseous species. For Equation 6.6.4 to be valid, the identity of the particles present cannot have an effect. Thus an ideal gas must be one whose properties are not affected by either the size of the particles or their intermolecular interactions because both will vary from one gas to another. The calculation of total and partial pressures for mixtures of gases is illustrated in Example \(\PageIndex{1}\).
Deep-sea divers must use special gas mixtures in their tanks, rather than compressed air, to avoid serious problems, most notably a condition called “the bends.” At depths of about 350 ft, divers are subject to a pressure of approximately 10 atm. A typical gas cylinder used for such depths contains 51.2 g of \(O_2\) and 326.4 g of He and has a volume of 10.0 L. What is the partial pressure of each gas at 20.00°C, and what is the total pressure in the cylinder at this temperature?
Given: masses of components, total volume, and temperature
Asked for: partial pressures and total pressure
Strategy:
- Calculate the number of moles of \(He\) and \(O_2\) present.
- Use the ideal gas law to calculate the partial pressure of each gas. Then add together the partial pressures to obtain the total pressure of the gaseous mixture.
Solution:
A The number of moles of \(He\) is
\[n_{\rm He}=\rm\dfrac{326.4\;g}{4.003\;g/mol}=81.54\;mol\]
The number of moles of \(O_2\) is
\[n_{\rm O_2}=\rm \dfrac{51.2\;g}{32.00\;g/mol}=1.60\;mol\]
B We can now use the ideal gas law to calculate the partial pressure of each:
\[P_{\rm He}=\dfrac{n_{\rm He}RT}{V}=\rm\dfrac{81.54\;mol\times0.08206\;\dfrac{atm\cdot L}{mol\cdot K}\times293.15\;K}{10.0\;L}=196.2\;atm\]
\[P_{\rm O_2}=\dfrac{n_{\rm O_2} RT}{V}=\rm\dfrac{1.60\;mol\times0.08206\;\dfrac{atm\cdot L}{mol\cdot K}\times293.15\;K}{10.0\;L}=3.85\;atm\]
The total pressure is the sum of the two partial pressures:
\[P_{\rm tot}=P_{\rm He}+P_{\rm O_2}=\rm(196.2+3.85)\;atm=200.1\;atm\]
A cylinder of compressed natural gas has a volume of 20.0 L and contains 1813 g of methane and 336 g of ethane. Calculate the partial pressure of each gas at 22.0°C and the total pressure in the cylinder.
Answer: \(P_{CH_4}=137 \; atm\); \(P_{C_2H_6}=13.4\; atm\); \(P_{tot}=151\; atm\)
Mole Fractions of Gas Mixtures
The composition of a gas mixture can be described by the mole fractions of the gases present. The mole fraction (\(X\)) of any component of a mixture is the ratio of the number of moles of that component to the total number of moles of all the species present in the mixture (\(n_{tot}\)):
\[x_A=\dfrac{\text{moles of A}}{\text{total moles}}= \dfrac{n_A}{n_{tot}} =\dfrac{n_A}{n_A+n_B+\cdots}\label{6.6.5}\]
The mole fraction is a dimensionless quantity between 0 and 1. If \(x_A = 1.0\), then the sample is pure \(A\), not a mixture. If \(x_A = 0\), then no \(A\) is present in the mixture. The sum of the mole fractions of all the components present must equal 1.
To see how mole fractions can help us understand the properties of gas mixtures, let’s evaluate the ratio of the pressure of a gas \(A\) to the total pressure of a gas mixture that contains \(A\). We can use the ideal gas law to describe the pressures of both gas \(A\) and the mixture: \(P_A = n_ART/V\) and \(P_{tot} = n_tRT/V\). The ratio of the two is thus
\[\dfrac{P_A}{P_{tot}}=\dfrac{n_ART/V}{n_{tot}RT/V} = \dfrac{n_A}{n_{tot}}=x_A \label{6.6.6}\]
Rearranging this equation gives
\[P_A = x_AP_{tot} \label{6.6.7}\]
That is, the partial pressure of any gas in a mixture is the total pressure multiplied by the mole fraction of that gas. This conclusion is a direct result of the ideal gas law, which assumes that all gas particles behave ideally. Consequently, the pressure of a gas in a mixture depends on only the percentage of particles in the mixture that are of that type, not their specific physical or chemical properties. By volume, Earth’s atmosphere is about 78% \(N_2\), 21% \(O_2\), and 0.9% \(Ar\), with trace amounts of gases such as \(CO_2\), \(H_2O\), and others. This means that 78% of the particles present in the atmosphere are \(N_2\); hence the mole fraction of \(N_2\) is 78%/100% = 0.78. Similarly, the mole fractions of \(O_2\) and \(Ar\) are 0.21 and 0.009, respectively. Using Equation 6.6.7, we therefore know that the partial pressure of N2 is 0.78 atm (assuming an atmospheric pressure of exactly 760 mmHg) and, similarly, the partial pressures of \(O_2\) and \(Ar\) are 0.21 and 0.009 atm, respectively.
We have just calculated the partial pressures of the major gases in the air we inhale. Experiments that measure the composition of the air we exhale yield different results, however. The following table gives the measured pressures of the major gases in both inhaled and exhaled air. Calculate the mole fractions of the gases in exhaled air.
| Inhaled Air / mmHg | Exhaled Air / mmHg | |
| \(P_{\rm N_2}\) | 597 | 568 |
| \(P_{\rm O_2}\) | 158 | 116 |
| \(P_{\rm H_2O}\) | 0.3 | 28 |
| \(P_{\rm CO_2}\) | 5 | 48 |
| \(P_{\rm Ar}\) | 8 | 8 |
| \(P_{tot}\) | 767 | 767 |
Given: pressures of gases in inhaled and exhaled air
Asked for: mole fractions of gases in exhaled air
Strategy:
Calculate the mole fraction of each gas using Equation 6.6.7.
Solution:
The mole fraction of any gas \(A\) is given by
\[x_A=\dfrac{P_A}{P_{tot}}\]
where \(P_A\) is the partial pressure of \(A\) and \(P_{tot}\) is the total pressure. For example, the mole fraction of \(CO_2\) is given as:
\[x_{\rm CO_2}=\rm\dfrac{48\;mmHg}{767\;mmHg}=0.063\]
The following table gives the values of \(x_A\) for the gases in the exhaled air.
| Gas | Mole Fraction |
| \({\rm N_2}\) | 0.741 |
| \({\rm O_2}\) | 0.151 |
| \({\rm H_2O}\) | 0.037 |
| \({\rm CO_2}\) | 0.063 |
| \({\rm Ar}\) | 0.010 |
Venus is an inhospitable place, with a surface temperature of 560°C and a surface pressure of 90 atm. The atmosphere consists of about 96% CO2 and 3% N2, with trace amounts of other gases, including water, sulfur dioxide, and sulfuric acid. Calculate the partial pressures of CO2 and N2.
Answer
\(P_{\rm CO_2}=\rm86\; atm\), \(P_{\rm N_2}=\rm2.7\;atm\)
Dalton’s Law of Partial Pressures: https://youtu.be/y5-SbspyvBA
Summary
- The partial pressure of each gas in a mixture is proportional to its mole fraction.
The pressure exerted by each gas in a gas mixture (its partial pressure) is independent of the pressure exerted by all other gases present. Consequently, the total pressure exerted by a mixture of gases is the sum of the partial pressures of the components (Dalton’s law of partial pressures). The amount of gas present in a mixture may be described by its partial pressure or its mole fraction. The mole fraction of any component of a mixture is the ratio of the number of moles of that substance to the total number of moles of all substances present. In a mixture of gases, the partial pressure of each gas is the product of the total pressure and the mole fraction of that gas.

