9.3: Concentration

 Learning Objectives

• Calculate percentage concentration (m/m, v/v, m/v), ppm and ppb.
• Calculate the molarity of a solution.
• Use concentration units to calculate the amount of solute in a solution.
• Use molarity to determine quantities in chemical reactions.
• Determine the resulting concentration of a diluted solution.

To define a solution precisely, we need to state its concentration: how much solute is dissolved in a certain amount of solvent. Words such as dilute or concentrated are used to describe solutions that have a little or a lot of dissolved solute, respectively, but these are relative terms whose meanings depend on various factors.

Solubility

There is usually a limit to how much solute will dissolve in a given amount of solvent. This limit is called the solubility of the solute. Some solutes have a very small solubility, while other solutes are soluble in all proportions. Table \(\PageIndex{1}\) lists the solubilities of various solutes in water. Solubilities vary with temperature, so Table \(\PageIndex{1}\) includes the temperature at which the solubility was determined.

Table \(\PageIndex{1}\): Solubilities of Various Solutes in Water at 25°C (Except as Noted)

Substance	Solubility (g in 100 mL of H2O)
AgCl(s)	0.019
C6H6(ℓ) (benzene)	0.178
CH4(g)	0.0023
CO2(g)	0.150
CaCO3(s)	0.058
CaF2(s)	0.0016
Ca(NO3)2(s)	143.9
C6H12O6 (glucose)	120.3 (at 30°C)
KBr(s)	67.8
MgCO3(s)	2.20
NaCl(s)	36.0
NaHCO3(s)	8.41
C12H22O11 (sucrose)	204.0 (at 20°C)

If a solution contains so much solute that its solubility limit is reached, the solution is said to be saturated, and its concentration is known from information contained in Table \(\PageIndex{1}\). If a solution contains less solute than the solubility limit, it is unsaturated. Under special circumstances, more solute can be dissolved even after the normal solubility limit is reached; such solutions are called supersaturated and are not stable. If the solute is solid, excess solute can easily recrystallize. If the solute is a gas, it can bubble out of solution uncontrollably, like what happens when you shake a soda can and then immediately open it.

Precipitation from Supersaturated Solutions

Recrystallization of excess solute from a supersaturated solution usually gives off energy as heat. Commercial heat packs containing supersaturated sodium acetate (NaC₂H₃O₂) take advantage of this phenomenon. You can probably find them at your local drugstore.

Video \(\PageIndex{1}\): Watered-down sodium acetate trihydrate. Needle crystal is truly wonderful structures

Most solutions we encounter are unsaturated, so knowing the solubility of the solute does not accurately express the amount of solute in these solutions. There are several common ways of specifying the concentration of a solution.

Percent Composition

There are several ways of expressing the concentration of a solution by using a percentage. The mass/mass percent (% m/m) is defined as the mass of a solute divided by the mass of a solution times 100:

\[\mathrm{\% \:m/m = \dfrac{mass\: of\: solute}{mass\: of\: solution}\times100\%} \nonumber \]

If you can measure the masses of the solute and the solution, determining the mass/mass percent is easy. Each mass must be expressed in the same units to determine the proper concentration.

Example \(\PageIndex{1}\)

A saline solution with a mass of 355 g has 36.5 g of NaCl dissolved in it. What is the mass/mass percent concentration of the solution?

Solution

We can substitute the quantities given in the equation for mass/mass percent:

\(\mathrm{\%\: m/m=\dfrac{36.5\: g}{355\: g}\times100\%=10.3\%}\)

Exercise \(\PageIndex{1}\)

A dextrose (also called D-glucose, C₆H₁₂O₆) solution with a mass of 2.00 × 10² g has 15.8 g of dextrose dissolved in it. What is the mass/mass percent concentration of the solution?

Answer

7.90%

For gases and liquids, volumes are relatively easy to measure, so the concentration of a liquid or a gas solution can be expressed as a volume/volume percent (% v/v): the volume of a solute divided by the volume of a solution times 100:

\[\mathrm{\%\: v/v = \dfrac{volume\: of\: solute}{volume\: of\: solution}\times100\%} \nonumber \]

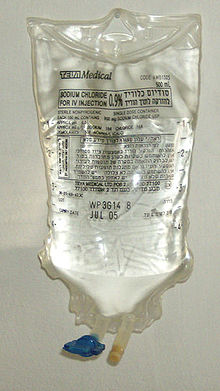
Again, the units of the solute and the solution must be the same. A hybrid concentration unit, mass/volume percent (% m/v), is commonly used for intravenous (IV) fluids (Figure \(\PageIndex{1}\)). It is defined as the mass in grams of a solute, divided by volume in milliliters of solution times 100:

\[\mathrm{\%\: m/v = \dfrac{mass\: of\: solute\: (g)}{volume\: of\: solution\: (mL)}\times100\%} \nonumber \]

Figure \(\PageIndex{1}\): Mass/Volume Percent.The 0.9% NaCl concentration on this IV bag is mass/volume percent (left). Such solution is used for other purposes and available in bottles (right). Figures used with permission from Wikipedia

Using Percent Composition in Calculations

The percent concentration can be used to produce a conversion factor between the amount of solute and the amount of solution. As such, concentrations can be useful in a variety of stoichiometry problems as discussed in Chapter 6. In many cases, it is best to use the original definition of the concentration unit; it is that definition that provides the conversion factor.

As an example, if the given concentration is 5% v/v solution of alcohol, this means that there are 5 mL of alcohol dissolved in every 100 mL solution.

5 mL alcohol = 100 mL solution

The two possible conversion factors are written as follows:

\(\mathrm{\dfrac{5\: mL\: alcohol}{100\: mL\: solution}}\) or \(\mathrm{\dfrac{100\: mL\: solution}{5\: mL\: alcohol}}\)

Use the first conversion factor to convert from a given amount of solution to amount of solute. The second conversion factor is used to convert from a given amount of solute to amount of solution. Given any two quantities in any percent composition, the third quantity can be calculated, as the following example illustrates.

Example \(\PageIndex{2}\)

A sample of 45.0% v/v solution of ethanol (C₂H₅OH) in water has a volume of 115 mL. What volume of ethanol solute does the sample contain?

Solution

A percentage concentration is simply the number of parts of solute per 100 parts of solution. Thus, the percent concentration of 45.0% v/v implies the following:

\(\mathrm{45.0\%\: v/v \rightarrow \dfrac{45\: mL\: C_2H_5OH}{100\: mL\: solution}}\)

That is, there are 45 mL of C₂H₅OH for every 100 mL of solution. We can use this fraction as a conversion factor to determine the amount of C₂H₅OH in 115 mL of solution:

\(\mathrm{115\: mL\: solution\times\dfrac{45\: mL\: C_2H_5OH}{100\: mL\: solution}=51.8\: mL\: C_2H_5OH}\)

Exercise \(\PageIndex{2}\)

What volume of a 12.75% m/v solution of glucose (C₆H₁₂O₆) in water is needed to obtain 50.0 g of C₆H₁₂O₆?

Answer

\(\mathrm{50.0\: g\: C_6H_12O_6\times\dfrac{100\: mL\: solution}{12.75\: g\: C_6H_12O_6}=392\: mL\: solution}\)

Example \(\PageIndex{3}\)

A normal saline IV solution contains 9.0 g of NaCl in every liter of solution. What is the mass/volume percent of normal saline?

Solution

We can use the definition of mass/volume percent, but first we have to express the volume in milliliter units:

1 L = 1,000 mL

Because this is an exact relationship, it does not affect the significant figures of our result.

\(\mathrm{\%\: m/v = \dfrac{9.0\: g\: NaCl}{1,000\: mL\: solution}\times100\%=0.90\%\: m/v}\)

Exercise \(\PageIndex{3}\)

The chlorine bleach that you might find in your laundry room is typically composed of 27.0 g of sodium hypochlorite (NaOCl), dissolved to make 500.0 mL of solution. What is the mass/volume percent of the bleach?

Answer

\(\mathrm{\%\: m/v = \dfrac{27.0\: g\: NaOCl}{500.0\: mL\: solution}\times100\%=5.40\%\: m/v}\)

In addition to percentage units, the units for expressing the concentration of extremely dilute solutions are parts per million (ppm) and parts per billion (ppb). Both of these units are mass based and are defined as follows:

\[\mathrm{ppm=\dfrac{mass\: of\: solute}{mass\: of\: solution}\times1,000,000} \nonumber \]

\[\mathrm{ppb=\dfrac{mass\: of\: solute}{mass\: of\: solution}\times1,000,000,000} \nonumber \]

Similar to parts per million and parts per billion, related units include parts per thousand (ppth) and parts per trillion (ppt).

Concentrations of trace elements in the body—elements that are present in extremely low concentrations but are nonetheless necessary for life—are commonly expressed in parts per million or parts per billion. Concentrations of poisons and pollutants are also described in these units. For example, cobalt is present in the body at a concentration of 21 ppb, while the State of Oregon’s Department of Agriculture limits the concentration of arsenic in fertilizers to 9 ppm.

In aqueous solutions, 1 ppm is essentially equal to 1 mg/L, and 1 ppb is equivalent to 1 µg/L.

Example \(\PageIndex{4}\)

If the concentration of cobalt in a human body is 21 ppb, what mass in grams of Co is present in a body having a mass of 70.0 kg?

Solution

A concentration of 21 ppb means “21 g of solute per 1,000,000,000 g of solution.” Written as a conversion factor, this concentration of Co is as follows:

\(\mathrm{21\: ppb\: Co \rightarrow \dfrac{21\: g\: Co}{1,000,000,000\: g\: solution}}\)

We can use this as a conversion factor, but first we must convert 70.0 kg to gram units:

\(\mathrm{70.0\: kg\times\dfrac{1,000\: g}{1\: kg}=7.00\times10^4\: g}\)

Now we determine the amount of Co:

\(\mathrm{7.00\times10^4\: g\: solution\times\dfrac{21\: g\: Co}{1,000,000,000\: g\: solution}=0.0015\: g\: Co}\)

This is only 1.5 mg.

Exercise \(\PageIndex{4}\)

An 85 kg body contains 0.012 g of Ni. What is the concentration of Ni in parts per million?

Answer

0.14 ppm

Molarity

Another way of expressing concentration is to give the number of moles of solute per unit volume of solution. Such concentration units are useful for discussing chemical reactions in which a solute is a product or a reactant. Molar mass can then be used as a conversion factor to convert amounts in moles to amounts in grams.

Molarity is defined as the number of moles of a solute dissolved per liter of solution:

\[\mathrm{molarity=\dfrac{number\: of\: moles\: of\: solute}{number\: of\: liters\: of\: solution}} \nonumber \]

Molarity is abbreviated M (often referred to as “molar”), and the units are often abbreviated as mol/L. It is important to remember that “mol” in this expression refers to moles of solute and that “L” refers to liters of solution. For example, if you have 1.5 mol of NaCl dissolved in 0.500 L of solution, its molarity is therefore

\[\mathrm{\dfrac{1.5\: mol\: NaCl}{0.500\: L\: solution}=3.0\: M\: NaCl} \nonumber \]

which is read as “three point oh molar sodium chloride.” Sometimes (aq) is added when the solvent is water, as in “3.0 M NaCl(aq).”

Before a molarity concentration can be calculated, the amount of the solute must be expressed in moles, and the volume of the solution must be expressed in liters.

If the quantity of the solute is given in mass units, you must convert mass units to mole units before using the definition of molarity to calculate concentration. For example, what is the molar concentration of a solution of 22.4 g of HCl dissolved in 1.56 L?

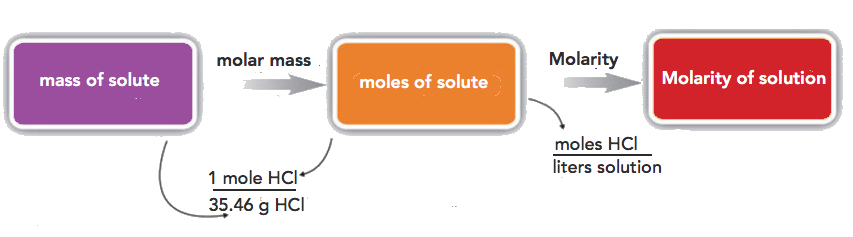
Step 1: convert the mass of solute to moles using the molar mass of HCl (36.46 g/mol):

\[22.4\cancel{gHCl}\times \dfrac{1\: mol\: HCl}{36.46\cancel{gHCl}}=0.614\, mol\; HCl \nonumber \]

Step 2: use the definition of molarity to determine the concentration:

\[M \: =\: \dfrac{0.614\: mol\: HCl}{1.56L\: solution}=0.394\, M HCl \nonumber \]

Example \(\PageIndex{5}\)

What is the molarity of an aqueous solution of 25.0 g of NaOH in 750 mL?

Solution

Before we substitute these quantities into the definition of molarity, we must convert them to the proper units. The mass of NaOH must be converted to moles of NaOH. The molar mass of NaOH is 40.00 g/mol:

\(\mathrm{25.0\: g\: NaOH\times\dfrac{1\: mol\: NaOH}{40.00\: g\: NaOH}=0.625\: mol\: NaOH}\)

Next, we convert the volume units from milliliters to liters:

\(\mathrm{750\: mL\times\dfrac{1\: L}{1,000\: mL}=0.750\: L}\)

Now that the quantities are expressed in the proper units, we can substitute them into the definition of molarity:

\(\mathrm{M=\dfrac{0.625\: mol\: NaOH}{0.750\: L}=0.833\: M\: NaOH}\)

Exercise \(\PageIndex{5}\)

If a 350 mL cup of coffee contains 0.150 g of caffeine (C₈H₁₀N₄O₂), what is the molarity of this caffeine solution?

Answer

0.00221 M

Using Molarity in Calculations

The definition of molarity can also be used to calculate a needed volume of solution, given its concentration and the number of moles desired, or the number of moles of solute (and subsequently, the mass of the solute), given its concentration and volume. As in the percent concentration, molarity can also be expressed as a conversion factor.

Molarity is defined as moles solute per liter solution. There is an understood 1 in the denominator of the conversion factor. For example, a 3.0 M solution of sucrose means that there are three moles of sucrose dissolved in every liter of solution. Mathematically, this is stated as follows:

3.0 moles sucrose = 1 L solution

Dividing both sides of this expression by either side, we generate two possible conversion factors:

\(\mathrm{\dfrac{3.0\: mol\: sucrose}{1\: L\: solution}}\) or \(\mathrm{\dfrac{1\: L\: solution}{3.0\: mol\: sucrose}}\)

The first conversion factor can be used to convert from volume (L) of solution to moles solute, and the second converts from moles of solute to volume (L) of solution.

For example, suppose we are asked how many moles of sucrose are present in 0.108 L of a 3.0 M sucrose solution. The given volume (0.108 L) is multiplied by the first conversion factor to cancel the L units, and find that 0.32 moles of sucrose are present.

\[0.108\cancel{L\, solution}\times \dfrac{3.0\, mol\, sucrose}{\cancel{1L\, solution}}=0.32\, mol\, sucrose \nonumber \]

How many liters of 3.0 M sucrose solution are needed to obtain 4.88 mol of sucrose? In such a conversion, we multiply the given (4.88 moles sucrose) with the second conversion factor. This cancels the moles units and converts it to liters of solution.

\[4.88\cancel{mol\, sucrose}\times \dfrac{1\, L\, solution}{\cancel{3.0\, mol\, sucrose}}=1.63\, L\, solution \nonumber \]

Example \(\PageIndex{6}\)

1. What volume of a 0.0753 M solution of dimethylamine [(CH₃)₂NH] is needed to obtain 0.450 mol of the compound?
2. Ethylene glycol (C₂H₆O₂) is mixed with water to make auto engine coolants. How many grams of C₂H₆O₂ are in 5.00 L of a 6.00 M aqueous solution?

Solution

1. To solve for the volume, multiply the "given" (0.450 mol of dimethylamine) with the molarity conversion factor (0.0753 M). Use the proper conversion factor to cancel the unit "mol" and get the unit volume (L) of solution:

\(\mathrm{0.450\: mol\: dimethylamine\times\dfrac{1\: L\: solution}{0.0753\: mol\: dimethylamine}=5.98\: L\: solution}\)

2. The strategy in solving this problem is to convert the given volume (5.00 L) using the 6.00 M (conversion factor) to solve for moles of ethylene glycol, which can then be converted to grams.

Step 1: Convert the given volume (5.00 L) to moles ethylene glycol.

\(\mathrm{5.00\: L\: solution\times\dfrac{6.00\: mol\: C_2H_6O_2}{1\: L\: solution}=30.0\: mol\: C_2H_6O_2}\)

Step 2: Convert 30.0 mols C₂H₆O₂ to grams C₂H₆O₂. Molar mass of C₂H₆O₂= 62.08 g/mol

\(\mathrm{30.0\: mol\: C_2H_6O_2\times\dfrac{62.08\: g\: C_2H_6O_2}{1\: mol\: C_2H_6O_2}=1,860\: g\: C_2H_6O_2}\)

The same two-step problem can also be worked out in a single line, rather than as two separate steps, as follows:

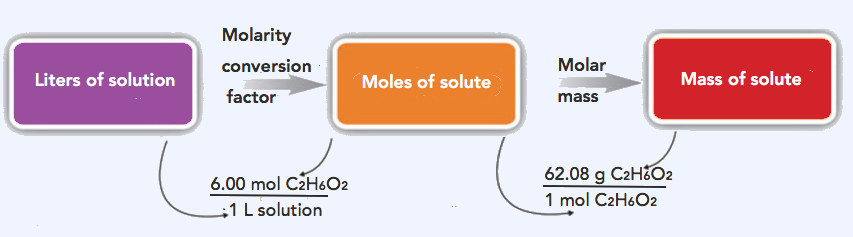
\(\mathrm{5.00\: L\: solution\times\dfrac{6.00\: mol\: C_2H_6O_2}{1\: L\: solution}\times\dfrac{62.08\: g\: C_2H_6O_2}{1\: mol\: C_2H_6O_2}=1,860\: g\: C_2H_6O_2}\)

The final answer is rounded off to 3 significant figures. Thus, there are 1,860 g of C₂H₆O₂ in the specified amount of engine coolant.

Note: Dimethylamine has a “fishy” odor. In fact, organic compounds called amines cause the odor of decaying fish.

Example \(\PageIndex{6A}\)

1. What volume of a 0.0753 M solution of dimethylamine [(CH₃)₂NH] is needed to obtain 0.450 mol of the compound?
2. Ethylene glycol (C₂H₆O₂) is mixed with water to make auto engine coolants. How many grams of C₂H₆O₂ are in 5.00 L of a 6.00 M aqueous solution?

Solution

This is an alternative method in case you don't want to use the conversion factor for molarity. In both parts, we will use the definition of molarity to solve for the desired quantity.

1. \(\mathrm{0.0753\: M=\dfrac{0.450\: mol\: (CH_3)_2NH}{volume\: of\: solution}}\)

To solve for the volume of solution, we multiply both sides by volume of solution and divide both sides by the molarity value to isolate the volume of solution on one side of the equation:

\(\mathrm{volume\:of\:solution = \dfrac{0.450\:mol\:(CH_3)_2NH}{0.0753\:M}=5.98\:L}\)

Note that because the definition of molarity is mol/L, the division of mol by M yields L, a unit of volume.

2. The molar mass of C₂H₆O₂ is 62.08 g/mol., so

\(\mathrm{6.00\: M=\dfrac{moles\: of\: solute}{5.00\: L}}\)

To solve for the number of moles of solute, we multiply both sides by the volume:

moles of solute = (6.00 M)(5.00 L) = 30.0 mol

Note that because the definition of molarity is mol/L, the product M × L gives mol, a unit of amount. Now, using the molar mass of C₃H₈O₃, we convert mol to g:

\(\mathrm{30.0\: mol\times\dfrac{62.08\: g}{mol}=1,860\: g}\)

Thus, there are 1,860 g of C₂H₆O₂ in the specified amount of engine coolant.

Exercise \(\PageIndex{6}\)

1. What volume of a 0.0902 M solution of formic acid (HCOOH) is needed to obtain 0.888 mol of HCOOH?
2. Acetic acid (HC₂H₃O₂) is the acid in vinegar. How many grams of HC₂H₃O₂ are in 0.565 L of a 0.955 M solution?

Answer

a. 9.84 L

b. 32.4 g

Using Molarity in Stoichiometry Problems

Of all the ways of expressing concentration, molarity is the one most commonly used in stoichiometry problems because it is directly related to the mole unit. Consider the following chemical equation:

HCl(aq) + NaOH(s) → H₂O(ℓ) + NaCl(aq)

Suppose we want to know how many liters of aqueous HCl solution will react with a given mass of NaOH. A typical approach to answering this question is as follows:

Figure \(\PageIndex{2}\): Typical approach to solving Molarity problems

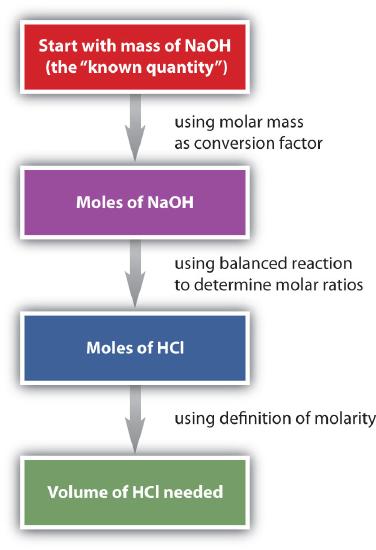
In itself, each step is a straightforward conversion. It is the combination of the steps that is a powerful quantitative tool for problem solving.

Example \(\PageIndex{7}\)

How many milliliters of a 2.75 M HCl solution are needed to react with 185 g of NaOH? The balanced chemical equation for this reaction is as follows:

HCl(aq) + NaOH(s) → H₂O(ℓ) + NaCl(aq)

Solution

We will follow the flowchart to answer this question. First, we convert the mass of NaOH to moles of NaOH using its molar mass, 40.00 g/mol:

\(\mathrm{185\: g\: NaOH\times\dfrac{1\: mol\: NaOH}{40.00\: g\: NaOH}=4.63\: mol\: NaOH}\)

Using the balanced chemical equation, we see that there is a one-to-one ratio of moles of HCl to moles of NaOH. We use this to determine the number of moles of HCl needed to react with the given amount of NaOH:

\(\mathrm{4.63\: mol\: NaOH\times\dfrac{1\: mol\: HCl}{1\: mol\: NaOH}=4.63\: mol\: HCl}\)

Finally, we use the definition of molarity to determine the volume of 2.75 M HCl needed:

\(\mathrm{2.75\: M\: HCl=\dfrac{4.63\: mol\: HCl}{volume\: of\: HCl\: solution}}\)

\(\mathrm{volume\: of\: HCl=\dfrac{4.63\: mol\: HCl}{2.75\: M\: HCl}=1.68\: L\times\dfrac{1,000\: mL}{1\: L}=1,680\: mL}\)

We need 1,680 mL of 2.75 M HCl to react with the NaOH.

The same multi-step problem can also be worked out in a single line, rather than as separate steps, as follows:

\(\mathrm{185\: g\: NaOH\times\dfrac{1\: mol\: NaOH}{40.00\: g\: NaOH}\times\dfrac{1\: mol\: HCl}{1\: mol\: NaOH}\times\dfrac{1\: L\: HCl\: solution}{2.75\: mol\: HCl}\times\dfrac{1000\: mL\: HCl\: solution}{1\: L\: HCl\: solution}=1,680\: mL\: HCl\: solution}\)

Our final answer (rounded off to three significant figures) is 1,680 mL HCl solution.

Exercise \(\PageIndex{7}\)

How many milliliters of a 1.04 M H₂SO₄ solution are needed to react with 98.5 g of Ca(OH)₂? The balanced chemical equation for the reaction is as follows:

\[H_2SO_{4(aq)} + Ca(OH)_{2(s)} \rightarrow 2H_2O_{(ℓ)} + CaSO_{4(aq)} \nonumber \]

Answer

1,280 mL

The general steps for performing stoichiometry problems such as this are shown in Figure \(\PageIndex{3}\). You may want to consult this figure when working with solutions in chemical reactions. The double arrows in Figure \(\PageIndex{3}\) indicate that you can start at either end of the chart and, after a series of simple conversions, determine the quantity at the other end.

Figure \(\PageIndex{3}\): Diagram of Steps for Using Molarity in Stoichiometry Calculations. When using molarity in stoichiometry calculations, a specific sequence of steps usually leads you to the correct answer.

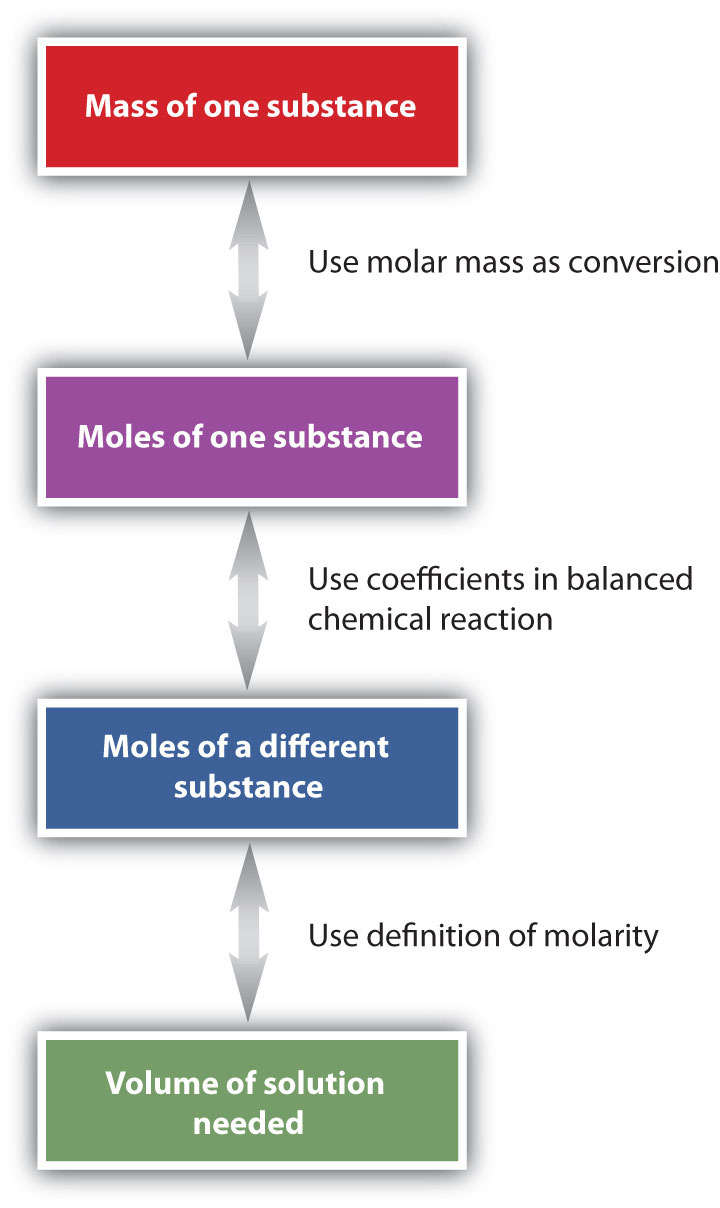
Many of the fluids found in our bodies are solutions. The solutes range from simple ionic compounds to complex proteins. Table \(\PageIndex{2}\) lists the typical concentrations of some of these solutes.

Table \(\PageIndex{2}\): Approximate Concentrations of Various Solutes in Some Solutions in the Body*

Solution	Solute	Concentration (M)
blood plasma	Na^+	0.138
	K^+	0.005
	Ca^2^+	0.004
	Mg^2^+	0.003
	Cl^−	0.110
	HCO3^−	0.030
stomach acid	HCl	0.10
urine	NaCl	0.15
	PO4^3^−	0.05
	NH2CONH2 (urea)	0.30
*Note: Concentrations are approximate and can vary widely.

Looking Closer: The Dose Makes the Poison

Why is it that we can drink 1 qt of water when we are thirsty and not be harmed, but if we ingest 0.5 g of arsenic, we might die? There is an old saying: the dose makes the poison. This means that what may be dangerous in some amounts may not be dangerous in other amounts.

Take arsenic, for example. Some studies show that arsenic deprivation limits the growth of animals such as chickens, goats, and pigs, suggesting that arsenic is actually an essential trace element in the diet. Humans are constantly exposed to tiny amounts of arsenic from the environment, so studies of completely arsenic-free humans are not available; if arsenic is an essential trace mineral in human diets, it is probably required on the order of 50 ppb or less. A toxic dose of arsenic corresponds to about 7,000 ppb and higher, which is over 140 times the trace amount that may be required by the body. Thus, arsenic is not poisonous in and of itself. Rather, it is the amount that is dangerous: the dose makes the poison.

Similarly, as much as water is needed to keep us alive, too much of it is also risky to our health. Drinking too much water too fast can lead to a condition called water intoxication, which may be fatal. The danger in water intoxication is not that water itself becomes toxic. It is that the ingestion of too much water too fast dilutes sodium ions, potassium ions, and other salts in the bloodstream to concentrations that are not high enough to support brain, muscle, and heart functions. Military personnel, endurance athletes, and even desert hikers are susceptible to water intoxication if they drink water but do not replenish the salts lost in sweat. As this example shows, even the right substances in the wrong amounts can be dangerous!

Equivalents

Concentrations of ionic solutes are occasionally expressed in units called equivalents (Eq). One equivalent equals 1 mol of positive or negative charge. Thus, 1 mol/L of Na⁺(aq) is also 1 Eq/L because sodium has a 1+ charge. A 1 mol/L solution of Ca²⁺(aq) ions has a concentration of 2 Eq/L because calcium has a 2+ charge. Dilute solutions may be expressed in milliequivalents (mEq)—for example, human blood plasma has a total concentration of about 150 mEq/L. (For more information about the ions present in blood plasma, see Chapter 3, Section 3.3.)

Dilutions

When additional water is added to an aqueous solution, the concentration of that solution decreases. This is because the number of moles of the solute does not change, while the volume of the solution increases. We can set up an equality between the moles of the solute before the dilution (1) and the moles of the solute after the dilution (2).

\[\text{mol}_1 = \text{mol}_2 \nonumber \]

Since the moles of solute in a solution is equal to the molarity multiplied by the liters, we can set those equal.

\[M_1 \times L_1 = M_2 \times L_2 \nonumber \]

Finally, because the two sides of the equation are set equal to one another, the volume can be in any units we choose, as long as that unit is the same on both sides. Our equation for calculating the molarity of a diluted solution becomes:

\[M_1 \times V_1 = M_2 \times V_2 \nonumber \]

Suppose that you have \(100. \: \text{mL}\) of a \(2.0 \: \text{M}\) solution of \(\ce{HCl}\). You dilute the solution by adding enough water to make the solution volume \(500. \: \text{mL}\). The new molarity can easily be calculated by using the above equation and solving for \(M_2\).

\[M_2 = \frac{M_1 \times V_1}{V_2} = \frac{2.0 \: \text{M} \times 100. \: \text{mL}}{500. \: \text{mL}} = 0.40 \: \text{M} \: \ce{HCl} \nonumber \]

The solution has been diluted by one-fifth since the new volume is five times as great as the original volume. Consequently, the molarity is one-fifth of its original value.

Figure \(\PageIndex{1}\): Figure \(\PageIndex{4}\): Diluting a solution by adding more solvent. Through the dilution process, the volume increases and the concentrations of the solutes decrease. As a consequence, there is more solution in the beaker after dilution, and the color of the solution becomes fainter. The inset shows that at the particular level (picometer to nanometer scale), there are less solute particles (red triangles) per volume. The content in the central box shows the dilution law, i.e. that the product of concentration and volume stays constant upon dilution. CC BY-SA 4.0.

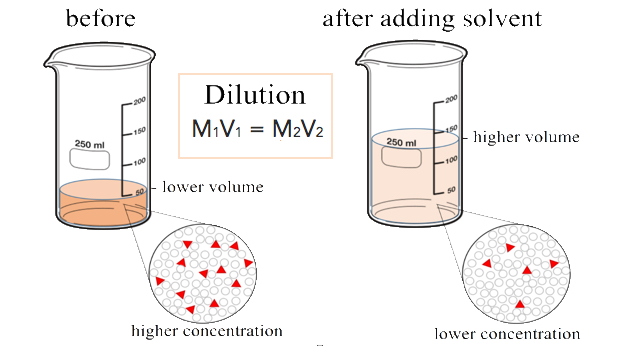
Dilution Equations

Any units of concentration and volume can be used, as long as both concentrations and both volumes have the same unit. For example, if we are using M (molarity), then we can express the equation as follows:

Molarity_initial × volume_{initial =} Molarity_final × volume_final or

M₁V₁ = M₂V₂

If we are using percent, the dilution equation is as follows:

%_initial × volume_{initial =} %_final × volume_final or

%₁V₁ = %₂V₂

Example \(\PageIndex{8}\)

A 125 mL sample of 0.900 M NaCl is diluted to 1,125 mL. What is the final concentration of the diluted solution?

Solution

Because the volume units are the same, and we are looking for the molarity of the final solution, we can use (concentration × volume)_initial = (concentration × volume)_final:

(0.900 M × 125 mL) = (concentration × 1,125 mL)

We solve by isolating the unknown concentration by itself on one side of the equation. Dividing by 1,125 mL gives

\(\mathrm{concentration = \dfrac{0.900\: M\times125\: mL}{1,125\: mL}=0.100\: M}\)

as the final concentration.

Exercise \(\PageIndex{8}\)

a. A nurse uses a syringe to inject 5.00 mL of 0.550 M heparin solution (heparin is an anticoagulant drug) into a 250 mL IV bag, for a final volume of 255 mL. What is the concentration of the resulting heparin solution?

b. A 0.885 M solution of KBr whose initial volume is 76.5 mL has more water added until its concentration is 0.500 M. What is the new volume of the solution?

Answer

a. 0.0108 M

b. 135.4 mL

Preparing IV Solutions

In a hospital emergency room, a physician orders an intravenous (IV) delivery of 100 mL of 0.5% KCl for a patient suffering from hypokalemia (low potassium levels). Does an aide run to a supply cabinet and take out an IV bag containing this concentration of KCl?

Not likely. It is more probable that the aide must make the proper solution from an IV bag of sterile solution and a more concentrated, sterile solution, called a stock solution, of KCl. The aide is expected to use a syringe to draw up some stock solution and inject it into the waiting IV bag and dilute it to the proper concentration. Thus the aide must perform a dilution calculation.

Figure \(\PageIndex{5}\):Preparing IV Solution © Thinkstock. Medical personnel commonly must perform dilutions for IV solutions.

If the stock solution is 10.0% KCl and the final volume and concentration need to be 100 mL and 0.50%, respectively, then it is an easy calculation to determine how much stock solution to use:

(10%)V₁ = (0.50%)(100 mL)

V₁ = 5 mL

Of course, the addition of the stock solution affects the total volume of the diluted solution, but the final concentration is likely close enough even for medical purposes.

Medical and pharmaceutical personnel are constantly dealing with dosages that require concentration measurements and dilutions. It is an important responsibility: calculating the wrong dose can be useless, harmful, or even fatal!

Key Takeaways

• Various concentration units are used to express the amounts of solute in a solution.
• Concentration units can be used as conversion factors in stoichiometry problems.
• New concentrations can be easily calculated if a solution is diluted.