2.1: Measuring Matter
- Page ID
- 204161
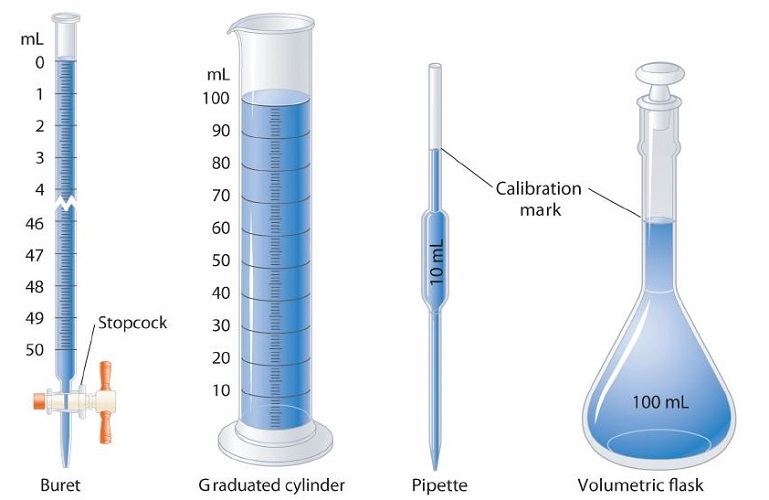
A variety of instruments are available for making direct measurements of the macroscopic properties of a chemical substance. For example, we usually measure the volume of a liquid sample with pipettes, burets, graduated cylinders, and volumetric flasks (Figure \(\PageIndex{1}\)), whereas we usually measure the mass of a solid or liquid substance with a balance (Figure \(\PageIndex{2}\)).
Instruments that Measure Volume
Many academic scientists report their volume measurements with the milliliter unit. On the other hand, analytical chemists tend to work with much smaller volumes, and they would use nanoliter and microliter samples in their laboratory. When considering the industrial realm, scientists work with larger volumes and would thus employ the liter unit of measurement.
Instruments that Measure Mass
Balances are utilized to measure the mass of matter. Typically, high school and middle schools will use triple beam balances for laboratory activities. Colleges will rely on digital balances. For larger quantities of materials, top-loading digital balances for employed. For higher sensitivity and accuracy, some chemists use analytical balances.

In the academic laboratory (like Furman University's), a chemist will commonly use the gram, or the even smaller unit, of the milligram. Industrial chemists making larger quantities of material would work with kilograms of materials. Analytical chemists (industrial or academic), environmental scientists, and toxicologists are typically more concerned with the smaller units of the metric system. For example, many chemicals found in drinking water and air are regulated in concentrations like nanograms and or micrograms.
Tools that Measure Length
Length is measured using a metric stick or a metric ruler marked in millimeters and centimeters. Most devices used to measure length (in the United States) contain both English and metric markings.

SI Units
All reported measurements must include an appropriate unit of measurement. To say that a substance has “a mass of 10” does not tell whether the mass was measured in grams, pounds, tons, or some other unit. For example, a nurse giving morphine to a patient needs to be specific in the unit dosages. A volume of liters would kill a patient quickly while a milliliter amount would provide sufficient pain relief. To establish worldwide standards for the consistent measurement of significant physical and chemical properties, an international body called the General Conference on Weights and Measures devised the Système Internationale d’unités (or SI). The International System of Units is based on metric units and requires that measurements be expressed in decimal form. Table \(\PageIndex{1}\) lists the seven base units of the SI system; all other SI units of measurement are derived from them.
| Base Quantity | Unit Name | Abbreviation |
|---|---|---|
| mass | kilogram | kg |
| length | meter | m |
| time | second | s |
| temperature | Kelvin | K |
The Metric System
| Prefix | Symbol | Value | Power of 10 | Meaning |
|---|---|---|---|---|
| tera | T | 1,000,000,000,000 | 1012 | trillion |
| giga | G | 1,000,000,000 | 109 | billion |
| mega | M | 1,000,000 | 106 | million |
| kilo | k | 1000 | 103 | thousand |
| hecto | h | 100 | 102 | hundred |
| deca | da | 10 | 101 | ten |
| — | — | 1 (this is base unit which could be gram, liter, or meter) | 100 | one |
| deci | d | 0.1 | 10−1 | tenth |
| centi | c | 0.01 | 10−2 | hundredth |
| milli | m | 0.001 | 10−3 | thousandth |
| micro | μ (medical community uses mcg) | 0.000001 | 10−6 | millionth |
| nano | n | 0.000000001 | 10−9 | billionth |
| pico | p | 0.000000000001 | 10−12 | trillionth |
| femto | f | 0.000000000000001 | 10−15 | quadrillionth |
Two methods of Memorization for the Metric System
Using negative exponents (see above) is the traditional way to memorize the metric system. Many students who have been taught outside of the United States approach the metric system this way. For their conversion factors, students who have been taught the metric system in the United States tend to use positive exponents. Either method is fine, pick one method and use it consistently.
Two different ways to memorize the metric systems (be sure to know all bolded conversion factors listed in section 2.1 of this OER)
- 1 gigabase = 1 x109 base
- 1 megabase = 1x106 base
- 1 kilobase = 1x103base
- 1 decibase = 1x10-1base or 1x101 decibase = 1 base
- 1 centibase = 1x10-2base or 1x102 centibase = 1 base
- 1 millibase = 1x10-3base or 1x103 millibase = 1 base
- 1 microbase = 1x10-6base or 1x106 microbase = 1 base
- 1 nanobase = 1x10-9base or 1x109 nanobase = 1 base
- 1 picobase = 1x10-12 base or 1x1012 picobase = 1 base
Note: A base unit can be gram, liter, or meter
Additional Units
When traveling to different regions of the globe, it is helpful to be able to convert from English to Metric units. The bolded conversions below may be helpful in travel and other situations. You may want to memorize them.
| Unit Conversion |
| 2.21 pounds = 1.00 kilograms |
| 1 mile = 1.61 kilometers |
| 1.00 inch = 2.54 centimeters |
| 1.00 mL = 1.00 cc (cubic centimeters) = 1.00 cm3 |
| 1 teaspoon (tsp) = 5.00 mL |
| 12 in = 1.00 ft. |
| 16 oz. = 1.00 pounds |
Scientific Notation
Chemists often work with numbers that are exceedingly large or small. For example, entering the mass in grams of a hydrogen atom into a calculator requires a display with at least 24 decimal places. A system called scientific notation avoids much of the tedium and awkwardness of manipulating numbers with large or small magnitudes. In scientific notation, these numbers are expressed in the form
\[ N \times 10^n\]
where N is greater than or equal to 1 and less than 10 (1 ≤ N < 10), and n is a positive or negative integer (100 = 1). The number 10 is called the base because it is this number that is raised to the power n. Although a base number may have values other than 10, the base number in scientific notation is always 10.
A simple way to convert numbers to scientific notation is to move the decimal point as many places to the left or right as needed to give a number between 1 to 10 (N). The magnitude of n is then determined as follows:
- If the decimal point is moved to the left n places, n is positive.
- If the decimal point is moved to the right n places, n is negative.
Another way to remember this is to recognize that as the number N decreases in magnitude, the exponent increases, and vice versa. The application of this rule is illustrated in Example \(\PageIndex{1}\).
Example \(\PageIndex{1}\): scientific notation
Convert each number to scientific notation.
- 637.8
- 0.0479
- 7.86
- 12,378
- 0.00032
- 61.06700
- 2002.080
- 0.01020
SOLUTION
| Explanation | Solution |
|---|---|
|
To convert 637.8 to a number from 1 to 10, we move the decimal point two places to the left: 6.378 Because the decimal point was moved two places to the left, n = 2. |
637.8 = 6.378 × 102 |
|
To convert 0.0479 to a number from 1 to 10, we move the decimal point two places to the right: 4.79 Because the decimal point was moved two places to the right, n = −2. |
0.0479 = 4.79 × 10−2 |
| This is usually expressed simply as 7.86. (Recall that 100 = 1). | 7.86 × 100 |
| Move the decimal point four places to the left and note a positive exponent. | 1.2378 × 104 |
| Move the decimal place four places to the right a note a negative exponent. | 3.2 × 10−4 |
| Move the decimal place one space to the left and note a positive exponent. | 6.106700 × 101 |
| Move the decimal place three places to the left and note a positive exponent. | 2.002080 × 103 |
| Move the decimal place two places to the right and note a negative exponent. | 1.020 × 10−2 |
Using the Scientific Calculator
Please be sure to obtain a calculator that has an exponent button on it. It will either say "exp" or have an "ee" key indicating this function. This key represents the function of 10x. You do not need to enter a 10 for an exponent when using this particular function. Read the steps below and practice on your calculator.
Use of Calculator
To input powers of ten:
- Locate the ee or exp button on your calculator. Do not use the carrot (looks like the ^ button).
- Put the coefficient number in and then hit "ee" or "exp."
- If you need to have a negative "exp," then locate the +/- button.
- Lastly, input your power of ten. You do not need to put the actual number ten in for the exponent.
Suggested Calculators
This is an image of calculators you could use in this class. You will need a non-programmable, scientific calculator that does not have metric conversion functions. In this picture, you will see the correct way to input one of the numbers shown in the example above. Please take time to practice with your calculator.

Contributors
- Hayden Cox (Furman University)


