18.4: Molar Reaction Enthalpy
- Page ID
- 238265
Recall that \(\Delta \overline{H}_\text{rxn}\) is a molar integral reaction enthalpy equal to \(\Delta H_\text{rxn}/\Delta \xi\), and that \(\Delta _rH\) is a molar differential reaction enthalpy defined by \(\sum_{i} \nu_{i} \ \overline{H}_{i}\) and equal to \((\partial H / \partial \xi)_{T, P}\).
Molar reaction enthalpy and heat
During a process in a closed system at constant pressure with expansion work only, the enthalpy change equals the energy transferred across the boundary in the form of heat: \(\mathrm{d} H=\mathrm{d} q\). Thus for the molar reaction enthalpy \(\Delta_{\mathrm{r}} H=(\partial H / \partial \xi)_{T, P}\), which refers to a process not just at constant pressure but also at constant temperature, we can write
\[\Delta_{\mathrm{r}} H=\left(\frac{\mathrm{d} q}{\mathrm{d} \xi}\right)_{T, P,w'}\label{1}\]
Note that when there is nonexpansion work (\(w'\)), such as electrical work, the enthalpy change is not equal to the heat. For example, if we compare a reaction taking place in a galvanic cell with the same reaction in a reaction vessel, the heats at constant \(T\) and \(P\) for a given change of \(\xi\) are different, and may even have opposite signs. The value of \( \Delta_{\mathrm{r}} H \) is the same in both systems, but the ratio of heat to extent of reaction, \(\mathrm{d} q / \mathrm{d} \xi\), is different.
An exothermic reaction is one for which \(\Delta_{\mathrm{r}} H\) is negative, and an endothermic reaction is one for which \(\Delta_{\mathrm{r}} H\) is positive. Thus in a reaction at constant temperature and pressure with expansion work only, heat is transferred out of the system during an exothermic process and into the system during an endothermic process. If the process takes place at constant pressure in a system with thermally-insulated walls, the temperature increases during an exothermic process and decreases during an endothermic process.
These comments apply not just to chemical reactions, but to the other chemical processes at constant temperature and pressure discussed in this chapter.
Standard molar enthalpies of reaction and formation
A standard molar reaction enthalpy, \(\Delta_{\mathrm{r}} H^{\circ}\), is the same as the molar integral reaction enthalpy \(\Delta \bar{H}_{\mathrm{rxn}}\) for the reaction taking place under standard state conditions (each reactant and product at unit activity) at constant temperature.
At constant temperature, partial molar enthalpies depend only mildly on pressure. It is therefore usually safe to assume that unless the experimental pressure is much greater than \(P^{\circ}\), the reaction is exothermic if \(\Delta_{\mathrm{r}} H^{\circ}\) is negative and endothermic if \(\Delta_{\mathrm{r}} H^{\circ}\) is positive.
The formation reaction of a substance is the reaction in which the substance, at a given temperature and in a given physical state, is formed from the constituent elements in their reference states at the same temperature. The reference state of an element is usually chosen to be the standard state of the element in the allotropic form and physical state that is stable at the given temperature and the standard pressure. For instance, at 298.15 K and 1 bar the stable allotrope of carbon is crystalline graphite rather than diamond.
Phosphorus is an exception to the rule regarding reference states of elements. Although red phosphorus is the stable allotrope at 298.15 K, it is not well characterized. Instead, the reference state is white phosphorus (crystalline P\(_4\)) at 1 bar.
At 298.15 K, the reference states of the elements are the following:
- For H\(_2\), N\(_2\), O\(_2\), F\(_2\), Cl\(_2\), and the noble gases, the reference state is the ideal gas at 1 bar.
- For Br\(_2\) and Hg, the reference state is the liquid at 1 bar.
- For P, as mentioned above, the reference state is crystalline white phosphorus at 1 bar.
- For all other elements, the reference state is the stable crystalline allotrope at 1 bar.
The standard molar enthalpy of formation (or standard molar heat of formation), \(\Delta_{f} H^{\circ}\), of a substance is the enthalpy change per amount of substance produced in the formation reaction of the substance in its standard state. Thus, the standard molar enthalpy of formation of gaseous methyl bromide at 298.15 K is the molar reaction enthalpy of the reaction
\[\mathrm{C}\left(\mathrm{s}, \text { graphite }, P^{\circ}\right)+\frac{3}{2} \mathrm{H}_{2}\left(\text { ideal gas, } P^{\circ}\right)+\frac{1}{2} \mathrm{Br}_{2}\left(1, P^{\circ}\right) \rightarrow \mathrm{CH}_{3} \mathrm{Br}\left(\text { ideal gas, } P^{\circ}\right)\nonumber\]
The value of \(\Delta_{f} H^{\circ}\) for a given substance depends only on \(T\). By definition, \(\Delta_{f} H^{\circ}\) for the reference state of an element is zero.
A principle called Hess’s law can be used to calculate the standard molar enthalpy of formation of a substance at a given temperature from standard molar reaction enthalpies at the same temperature, and to calculate a standard molar reaction enthalpy from tabulated values of standard molar enthalpies of formation. The principle is an application of the fact that enthalpy is a state function. Therefore, \(\Delta H\) for a given change of the state of the system is independent of the path and is equal to the sum of \(\Delta H\) values for any sequence of changes whose net result is the given change. (We may apply the same principle to a change of any state function.)
For example, the following combustion reactions can be carried out experimentally in a bomb calorimeter, yielding the values shown below of standard molar reaction enthalpies (at \(T = 298.15 \text{ K}\), \(P = P^{\circ} = 1 \text{ bar}\)):
\[\begin{aligned}
\mathrm{C}(\mathrm{s}, \text { graphite })+\mathrm{O}_{2}(\mathrm{g}) & \rightarrow \mathrm{CO}_{2}(\mathrm{g}) & \Delta_{\mathrm{r}} H^{\circ} &=-393.51 \text{ kJ} \text{ mol}^{-1} \\
\mathrm{CO}(\mathrm{g})+\frac{1}{2} \mathrm{O}_{2}(\mathrm{g}) & \rightarrow \mathrm{CO}_{2}(\mathrm{g}) & \Delta_{\mathrm{r}} H^{\circ} &=-282.98 \text{ kJ} \text{ mol}^{-1}
\end{aligned}\nonumber\]
(Note that the first reaction, in addition to being the combustion reaction of graphite, is also the formation reaction of carbon dioxide.) The change resulting from the first reaction followed by the reverse of the second reaction is the formation reaction of carbon monoxide:
\[\mathrm{C}(\mathrm{s}, \text { graphite })+\frac{1}{2} \mathrm{O}_{2}(\mathrm{g}) \rightarrow \mathrm{CO}(\mathrm{g})\nonumber\]
It would not be practical to measure the molar enthalpy of this last reaction by allowing graphite to react with oxygen in a calorimeter, because it would be difficult to prevent the formation of some CO\(_2\). From Hess’s law, the standard molar enthalpy of formation of CO is the sum of the standard molar enthalpies of the reactions that have the formation reaction as the net result:
\[\begin{aligned}
\Delta_{\mathrm{f}} H^{\circ}(\mathrm{CO}, \mathrm{g}, 298.15 \text{ K}) &=(-393.51+282.98) \text{ kJ} \text{ mol}^{-1} \\
&=-110.53 \text{ kJ} \text{ mol}^{-1}
\end{aligned}\]
This value is one of the many standard molar enthalpies of formation to be found in compilations of thermodynamic properties of individual substances. We may use the tabulated values to evaluate the standard molar reaction enthalpy \(\Delta_{\mathrm{r}} H^{\circ}\) of a reaction using a formula based on Hess’s law. Imagine the reaction to take place in two steps: First each reactant in its standard state changes to the constituent elements in their reference states (the reverse of a formation reaction), and then these elements form the products in their standard states. The resulting formula is:
\[\Delta_{\mathrm{r}} H^{\circ}=\sum_{i} \nu_{i} \Delta_{\mathrm{f}} H^{\circ}_i\label{2}\]
where \(\Delta_{\mathrm{f}} H^{\circ}_i\) is the standard molar enthalpy of formation of substance \(i\). Recall that the stoichiometric number \(\nu_i\) of each reactant is negative and that of each product is positive, so according to Hess’s law the standard molar reaction enthalpy is the sum of the standard molar enthalpies of formation of the products minus the sum of the standard molar enthalpies of formation of the reactants. Each term is multiplied by the appropriate stoichiometric coefficient from the reaction equation.
A standard molar enthalpy of formation can be defined for a solute in solution to use in \(\ref{2}\). For instance, the formation reaction of aqueous sucrose is:
\[12 \mathrm{C}(\mathrm{s}, \text { graphite })+11 \mathrm{H}_{2}(\mathrm{g})+\frac{11}{2} \mathrm{O}_{2}(\mathrm{g}) \rightarrow \mathrm{C}_{12} \mathrm{H}_{22} \mathrm{O}_{11}(\mathrm{aq})\nonumber\]
and \(\Delta_{\mathrm{f}} H^{\circ}_i\) for C\(_{12}\)H\(_{22}\)O\(_{11}\)(aq) is the enthalpy change per amount of sucrose formed when the reactants and product are in their standard states. Note that this formation reaction does not include the formation of the solvent H\(_2\)O from H\(_2\) and O\(_2\). Instead, the solute once formed combines with the amount of pure liquid water needed to form the solution. If the aqueous solute is formed in its standard state, the amount of water needed is very large so as to have the solute exhibit infinite-dilution behavior.
There is no ordinary reaction that would produce an individual ion in solution from its element or elements without producing other species as well. We can, however, prepare a consistent set of standard molar enthalpies of formation of ions by assigning a value to a single reference ion. We can use these values for ions in \(\ref{2}\) just like values of \(\Delta_{\mathrm{f}} H^{\circ}_i\) for substances and nonionic solutes. Aqueous hydrogen ion is the usual reference ion, to which is assigned the arbitrary value
\[\Delta_{\mathrm{f}} H^{\circ}\left(\mathrm{H}^{+}, \mathrm{aq}\right)=0 \quad \text { (at all temperatures) }\nonumber\]
To see how we can use this reference value, consider the reaction for the formation of aqueous HCl (hydrochloric acid):
\[\frac{1}{2} \mathrm{H}_{2}(\mathrm{g})+\frac{1}{2} \mathrm{Cl}_{2}(\mathrm{g}) \rightarrow \mathrm{H}^{+}(\mathrm{aq})+\mathrm{Cl}^{-}(\mathrm{aq})\nonumber\]
The standard molar reaction enthalpy at 298.15 K for this reaction is known, from reaction calorimetry, to have the value \(\Delta_{\mathrm{r}} H^{\circ}=-167.08 \text{ kJ} \text{ mol}^{-1}\). The standard states of the gaseous H\(_2\) and Cl\(_2\) are, of course, the pure gases acting ideally at pressure \(P^{\circ}\), and the standard state of each of the aqueous ions is the ion at the standard molality and standard pressure, acting as if its activity coefficient on a molality basis were \(1\). From \(ref{1}\), we equate the value of \(\Delta_{\mathrm{r}} H^{\circ}t\) to the sum
\[-\frac{1}{2} \Delta_{\mathrm{f}} H^{\circ}\left(\mathrm{H}_{2}, \mathrm{g}\right)-\frac{1}{2} \Delta_{\mathrm{f}} H^{\circ}\left(\mathrm{Cl}_{2}, \mathrm{g}\right)+\Delta_{\mathrm{f}} H^{\circ}\left(\mathrm{H}^{+}, \mathrm{aq}\right)+\Delta_{\mathrm{f}} H^{\circ}\left(\mathrm{Cl}^{-}, \mathrm{aq}\right)\]
But the first three terms of this sum are zero. Therefore, the value of \(\Delta_{\mathrm{f}} H^{\circ}\)(Cl\(^-\), aq) is \(-167.08 \text{ kJ mol}^{-1}\).
Next we can combine this value of \(\Delta_{\mathrm{f}} H^{\circ}\)(Cl\(^-\), aq) with the measured standard molar enthalpy of formation of aqueous sodium chloride
\[\mathrm{Na}(\mathrm{s})+\frac{1}{2} \mathrm{Cl}_{2}(\mathrm{g}) \rightarrow \mathrm{Na}^{+}(\mathrm{aq})+\mathrm{Cl}^{-}(\mathrm{aq})\nonumber\]
to evaluate the standard molar enthalpy of formation of aqueous sodium ion. By continuing this procedure with other reactions, we can build up a consistent set of \(\Delta_{\mathrm{f}} H^{\circ}\) values of various ions in aqueous solution.
Molar reaction heat capacity
The molar reaction enthalpy \(\Delta_\mathrm{r} \overline{H}\) is in general a function of \(T\), \(P\), and \(\xi\). Using the relations \(\Delta_\mathrm{r}H=\sum_i\!\nu_i H_i\) and \(C_{P, i}=\left(\partial H_{i} / \partial T\right)_{P, \xi}\), we can write
\[\left(\frac{\partial \Delta_{\mathrm{r}} H}{\partial T}\right)_{p, \xi}=\left(\frac{\partial \sum_{i} \nu_{i} H_{i}}{\partial T}\right)_{p, \xi}=\sum_{i} \nu_{i} C_{p, i}=\Delta_{\mathrm{r}} C_{p}\label{3}\]
where \(\Delta_\mathrm{r}C_P\) is the molar reaction heat capacity at constant pressure, equal to the rate at which the heat capacity \(C_P\) changes with \(\xi\) at constant \(T\) and \(P\).
Under standard state conditions, \(\ref{3}\) becomes
\[\mathrm{d} \Delta_{\mathrm{r}} H^{\circ} / \mathrm{d} T=\Delta_{\mathrm{r}} C_{p}^{\circ}\]
Effect of temperature on reaction enthalpy
Consider a reaction occurring with a certain finite change of the extent of reaction in a closed system at temperature \(T'\) and at constant pressure. The reaction is characterized by a change of the extent of reaction from \(\xi_1\) to \(\xi_2\), and the integral reaction enthalpy at this temperature is denoted \(\Delta H_{\mathrm{rxn}}\left(T^{\prime}\right)\). We wish to find an expression for the reaction enthalpy \(\Delta H_{\mathrm{rxn}}\left(T^{\prime \prime}\right)\) for the same values of \(\xi_1\) and \(\xi_2\) at the same pressure but at a different temperature, \(T''\).
The heat capacity of the system at constant pressure is related to the enthalpy: \(C_{P}=(\partial H / \partial T)_{P, \xi}\). We integrate \(\mathrm{d} H=C_{p} \mathrm{d} T\) from \(T'\) to \(T''\) at constant \(P\) and \(\xi\), for both the final and initial values of the extent of reaction:
\[H\left(\xi_{2}, T^{\prime \prime}\right)=H\left(\xi_{2}, T^{\prime}\right)+\int_{T^{\prime}}^{T^{\prime \prime}} C_{p}\left(\xi_{2}\right) \mathrm{d} T\label{4}\]
\[H\left(\xi_{1}, T^{\prime \prime}\right)=H\left(\xi_{1}, T^{\prime}\right)+\int_{T^{\prime}}^{T^{\prime \prime}} C_{p}\left(\xi_{1}\right) \mathrm{d} T\label{5}\]
Subtracting \(\ref{5}\) from \(\ref{4}\), we obtain
\[\Delta H_{\mathrm{rxn}}\left(T^{\prime \prime}\right)=\Delta H_{\mathrm{rxn}}\left(T^{\prime}\right)+\int_{T^{\prime}}^{T^{\prime \prime}} \Delta C_{p} \mathrm{d} T\label{6}\]
where \(\Delta C_P\) is the difference between the heat capacities of the system at the final and initial values of \(\xi\), a function of \(T\): \(\Delta C_{p}=C_{p}\left(\xi_{2}\right)-C_{p}\left(\xi_{1}\right)\). \(\ref{6}\) is the Kirchhoff equation.
When \(\Delta C_P\) is essentially constant in the temperature range from \(T'\) to \(T''\), the Kirchhoff equation becomes
\[\Delta H_{\mathrm{rxn}}\left(T^{\prime \prime}\right)=\Delta H_{\mathrm{rxn}}\left(T^{\prime}\right)+\Delta C_{p}\left(T^{\prime \prime}-T^{\prime}\right)\label{7}\]
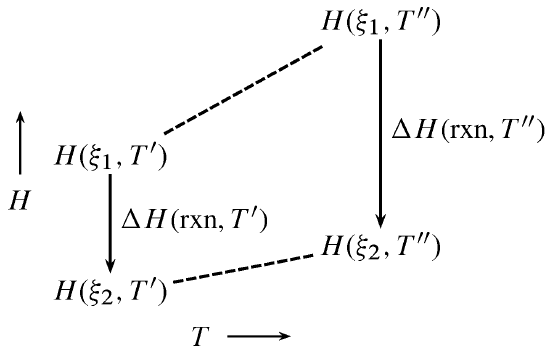
Figure \(\PageIndex{1}\): Dependence of reaction enthalpy on temperature at constant pressure.
Figure \(\PageIndex{1}\) illustrates the principle of the Kirchhoff equation as expressed by \(\ref{7}\). \(\Delta C_{P}\) equals the difference in the slopes of the two dashed lines in the figure, and the product of \(\Delta C_{P}\) and the temperature difference \(T''-T'\) equals the change in the value of \(\Delta H_\mathrm{rxn}\). The figure illustrates an exothermic reaction with negative \(\Delta C_{P}\), resulting in a more negative value of \(\Delta H_\mathrm{rxn}\) at the higher temperature.
We can also find the effect of temperature on the molar differential reaction enthalpy \(\Delta_\mathrm{r}H\). From \(\ref{3}\), we have \(C_{P}=(\partial H / \partial T)_{P, \xi}\). Integration from temperature \(T'\) to temperature \(T''\) yields the relation
\[\Delta_{\mathrm{r}} H\left(T^{\prime \prime}, \xi\right)=\Delta_{\mathrm{r}} H\left(T^{\prime}, \xi\right)+\int_{T^{\prime}}^{T^{\prime \prime}} \Delta_{\mathrm{r}} C_{p}(T, \xi) \mathrm{d} T\]
This relation is analogous to \(\ref{6}\), using molar differential reaction quantities in place of integral reaction quantities.
Contributors
- Howard DeVoe, Associate Professor Emeritus, University of Maryland from Thermodynamics and Chemistry

