14.16: Reading- The Collusion Model
- Page ID
- 249432
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The Collusion Model
There is no single model of profit-maximizing oligopoly behavior that corresponds to economists’ models of perfect competition, monopoly, and monopolistic competition. Uncertainty about the interaction of rival firms makes specification of a single model of oligopoly impossible. Instead, economists have devised a variety of models that deal with the uncertain nature of rivals’ responses in different ways. In this section we review one type of oligopoly model, the collusion model. After examining this traditional approach to the analysis of oligopoly behavior, we shall turn to another method of examining oligopolistic interaction: game theory.
Firms in any industry could achieve the maximum profit attainable if they all agreed to select the monopoly price and output and to share the profits. One approach to the analysis of oligopoly is to assume that firms in the industry collude, selecting the monopoly solution.
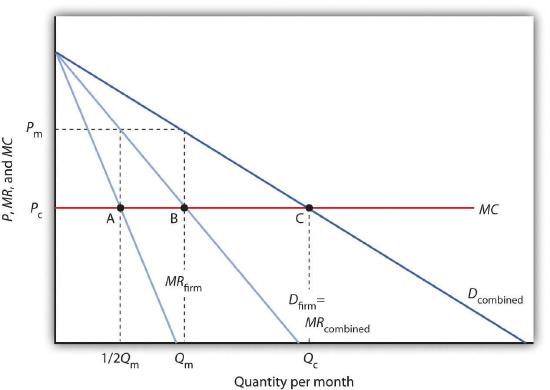
Suppose an industry is a duopoly, an industry with two firms. Figure 11.3 “Monopoly Through Collusion” shows a case in which the two firms are identical. They sell identical products and face identical demand and cost conditions. To simplify the analysis, we will assume that each has a horizontal marginal cost curve, MC. The demand and marginal revenue curves are the same for both firms. We find the combined demand curve for the two firms, Dcombined, by adding the individual demand curves together. Because one firm’s demand curve, Dfirm, represents one-half of market demand, it is the same as the combined marginal revenue curve for the two firms. If these two firms act as a monopoly, together they produce Qm and charge a price Pm. This result is achieved if each firm selects its profit-maximizing output, which equals 1/2 Qm. This solution is inefficient; the efficient solution is price Pc and output Qc, found where the combined market demand curveDcombined and the marginal cost curve MC intersect.
In the simplest form of collusion, overt collusion, firms openly agree on price, output, and other decisions aimed at achieving monopoly profits. Firms that coordinate their activities through overt collusion and by forming collusive coordinating mechanisms make up a cartel.
Firms form a cartel to gain monopoly power. A successful cartel can earn large profits, but there are several problems with forming and maintaining one. First, in many countries, including the United States, cartels are generally illegal.One legal cartel is the NCAA, which many economists regard as a successful device through which member firms (colleges and universities) collude on a wide range of rules through which they produce sports. They are banned, because their purpose is to raise prices and restrict output. Second, the cartel may not succeed in inducing all firms in the industry to join. Firms that remain outside the cartel can compete by lowering price, and thus they prevent the cartel from achieving the monopoly solution. Third, there is always an incentive for individual members to cheat on cartel agreements. Suppose the members of a cartel have agreed to impose the monopoly price in their market and to limit their output accordingly. Any one firm might calculate that it could charge slightly less than the cartel price and thus capture a larger share of the market for itself. Cheating firms expand output and drive prices down below the level originally chosen.
The Organization of Petroleum Exporting Countries (OPEC), perhaps the best-known cartel, is made up of 13 oil-producing countries. In the 1970s, OPEC successfully acted like a monopoly by restricting output and raising prices. By the mid-1980s, however, the monopoly power of the cartel had been weakened by expansion of output by nonmember producers such as Mexico and Norway and by cheating among the cartel members.
An alternative to overt collusion is tacit collusion, an unwritten, unspoken understanding through which firms agree to limit their competition. Firms may, for example, begin following the price leadership of a particular firm, raising or lowering their prices when the leader makes such a change. The price leader may be the largest firm in the industry, or it may be a firm that has been particularly good at assessing changes in demand or cost. At various times, tacit collusion has been alleged to occur in a wide range of industries, including steel, cars, and breakfast cereals.
It is difficult to know how common tacit collusion is. The fact that one firm changes its price shortly after another one does cannot prove that a tacit conspiracy exists. After all, we expect to see the prices of all firms in a perfectly competitive industry moving together in response to changes in demand or production costs.
Self Check: Collusion
Answer the question(s) below to see how well you understand the topics covered in the previous section. This short quiz does not count toward your grade in the class, and you can retake it an unlimited number of times.
You’ll have more success on the Self Check if you’ve completed the two Readings in this section.
Use this quiz to check your understanding and decide whether to (1) study the previous section further or (2) move on to the next section.
- Principles of Microeconomics Chapter 11.2. Authored by: OpenStax College. Located at: http://cnx.org/contents/ea2f225e-6063-41ca-bcd8-36482e15ef65@10.31:24/Microeconomics. License: CC BY: Attribution. License Terms: Download for free at http://cnx.org/content/col11627/latest

