Many nuclei are radioactive; that is, they decompose by emitting particles and in doing so, become a different nucleus. In our studies up to this point, atoms of one element were unable to change into different elements. That is because in all other types of changes discussed, only the electrons were changing. In these changes, the nucleus, which contains the protons that dictate which element an atom is, is changing. All nuclei with 84 or more protons are radioactive, and elements with less than 84 protons have both stable and unstable isotopes. All of these elements can go through nuclear changes and turn into different elements.
In natural radioactive decay, three common emissions occur. When these emissions were originally observed, scientists were unable to identify them as some already known particles and so named them:
These particles were named using the first three letters of the Greek alphabet. Some later time, alpha particles were identified as helium-4 nuclei, beta particles were identified as electrons, and gamma rays as a form of electromagnetic radiation like x-rays, except much higher in energy and even more dangerous to living systems.
The Ionizing and Penetration Power of Radiation
With all the radiation from natural and man-made sources, we should quite reasonably be concerned about how all the radiation might affect our health. The damage to living systems is done by radioactive emissions when the particles or rays strike tissue, cells, or molecules and alter them. These interactions can alter molecular structure and function; cells no longer carry out their proper function and molecules, such as DNA, no longer carry the appropriate information. Large amounts of radiation are very dangerous, even deadly. In most cases, radiation will damage a single (or very small number) of cells by breaking the cell wall or otherwise preventing a cell from reproducing.
The ability of radiation to damage molecules is analyzed in terms of what is called ionizing power. When a radiation particle interacts with atoms, the interaction can cause the atom to lose electrons and thus become ionized. The greater the likelihood that damage will occur by an interaction is the ionizing power of the radiation.
Much of the threat from radiation is involved with the ease or difficulty of protecting oneself from the particles. How thick of a wall do you need to hide behind to be safe? The ability of each type of radiation to pass through matter is expressed in terms of penetration power. The more material the radiation can pass through, the greater the penetration power and the more dangerous it is. In general, the greater mass present, the greater the ionizing power, and the lower the penetration power.
Comparing only the three common types of ionizing radiation, alpha particles have the greatest mass. Alpha particles have approximately four times the mass of a proton or neutron and approximately 8,000 times the mass of a beta particle. Because of the large mass of the alpha particle, it has the highest ionizing power and the greatest ability to damage tissue. That same large size of alpha particles, however, makes them less able to penetrate matter. They collide with molecules very quickly when striking matter, add two electrons, and become a harmless helium atom. Alpha particles have the least penetration power and can be stopped by a thick sheet of paper or even a layer of clothes. They are also stopped by the outer layer of dead skin on people. This may seem to remove the threat from alpha particles, but it is only from external sources. In a nuclear explosion or some sort of nuclear accident, where radioactive emitters are spread around in the environment, the emitters can be inhaled or taken in with food or water and once the alpha emitter is inside you, you have no protection at all.
Beta particles are much smaller than alpha particles and therefore, have much less ionizing power (less ability to damage tissue), but their small size gives them much greater penetration power. Most resources say that beta particles can be stopped by a one-quarter inch thick sheet of aluminum. Once again, however, the greatest danger occurs when the beta emitting source gets inside of you.
Gamma rays are not particles, but a high energy form of electromagnetic radiation (like x-rays, except more powerful). Gamma rays are energy that has no mass or charge. Gamma rays have tremendous penetration power and require several inches of dense material (like lead) to shield them. Gamma rays may pass all the way through a human body without striking anything. They are considered to have the least ionizing power and the greatest penetration power.
Table \(\PageIndex{1}\) Comparison of Penetrating Power,Ionizing Power and Shielding of Alpha and Beta Particles, and Gamma Rays.
| Alpha |
\(\alpha\) |
\(4 \mathrm{amu}\) |
Very Low |
Very High |
Paper Skin |
| Beta |
\(\beta\) |
\(1 / 2000 \mathrm{amu}\) |
Intermediate |
Intermediate |
Aluminum |
| Gamma |
\(\gamma\) |
0 (energy only) |
Very High |
Very Low |
2 inches lead |
The safest amount of radiation to the human body is zero. It is impossible to completely avoid ionizing radiation, so the next best goal is to be exposed to as little as possible. The two best ways to minimize exposure are to limit time of exposure, and to increase distance from the source.
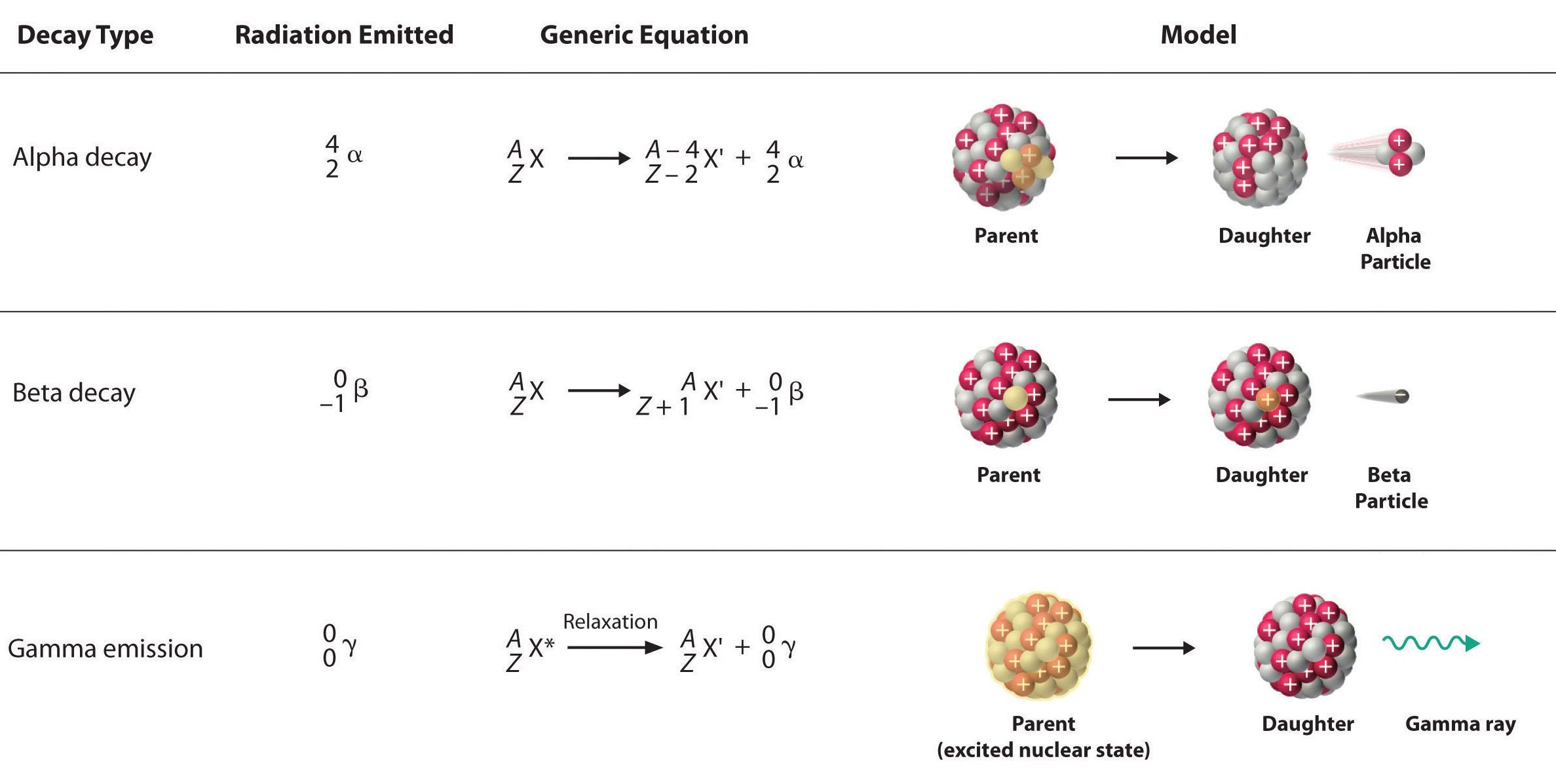
Alpha Decay
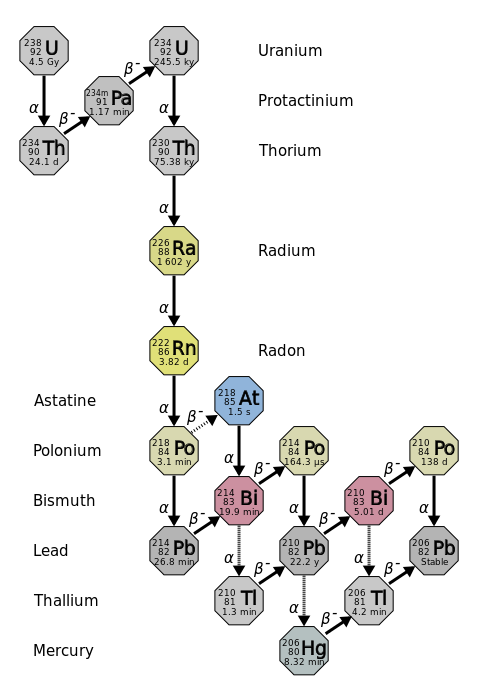
The nuclear disintegration process that emits alpha particles is called alpha decay. An example of a nucleus that undergoes alpha decay is uranium-238. The alpha decay of \(\ce{U}\)-238 is
\[\ce{_{92}^{238}U} \rightarrow \ce{_2^4He} + \ce{_{90}^{234}Th} \label{alpha1} \]
In this nuclear change, the uranium atom \(\left( \ce{_{92}^{238}U} \right)\) transmuted into an atom of thorium \(\left( \ce{_{90}^{234}Th} \right)\) and, in the process, gave off an alpha particle. Look at the symbol for the alpha particle: \(\ce{_2^4He}\). Where does an alpha particle get this symbol? The bottom number in a nuclear symbol is the number of protons. That means that the alpha particle has two protons in it that were lost by the uranium atom. The two protons also have a charge of \(+2\). The top number, 4, is the mass number or the total of the protons and neutrons in the particle. Because it has two protons, and a total of four protons and neutrons, alpha particles must also have two neutrons. Alpha particles always have this same composition: two protons and two neutrons.
Another alpha particle producer is thorium-230.
\[\ce{_{90}^{230}Th} \rightarrow \ce{_2^4He} + \ce{_{88}^{226}Ra} \label{alpha2} \]
These types of equations are called nuclear equations and are similar to the chemical equivalent discussed through the previous chapters.
Beta Decay
Another common decay process is beta particle emission, or beta decay. A beta particle is simply a high energy electron that is emitted from the nucleus. It may occur to you that we have a logically difficult situation here. Nuclei do not contain electrons and yet during beta decay, an electron is emitted from a nucleus. At the same time that the electron is being ejected from the nucleus, a neutron is becoming a proton. It is tempting to picture this as a neutron breaking into two pieces with the pieces being a proton and an electron. That would be convenient for simplicity, but unfortunately that is not what happens (more on this subject will be explained at the end of this section). For convenience, we will treat beta decay as a neutron splitting into a proton and an electron. The proton stays in the nucleus, increasing the atomic number of the atom by one. The electron is ejected from the nucleus and is the particle of radiation called beta.
To insert an electron into a nuclear equation and have the numbers add up properly, an atomic number and a mass number had to be assigned to an electron. The mass number assigned to an electron is zero (0), which is reasonable since the mass number is the number of protons plus neutrons, and an electron contains no protons and no neutrons. The atomic number assigned to an electron is negative one (-1), because that allows a nuclear equation containing an electron to balance atomic numbers. Therefore, the nuclear symbol representing an electron (beta particle) is
\(\ce{_{-1}^0e}\) or \(\ce{_{-1}^0\beta} \label{beta1}\)
Thorium-234 is a nucleus that undergoes beta decay. Here is the nuclear equation for this beta decay:
\[\ce{_{90}^{234}Th} \rightarrow \ce{_{-1}^0e} + \ce{_{91}^{234}Pa} \label{beta2} \]
Gamma Radiation
Frequently, gamma ray production accompanies nuclear reactions of all types. In the alpha decay of \(\ce{U}\)-238, two gamma rays of different energies are emitted in addition to the alpha particle.
\[\ce{_{92}^{238}U} \rightarrow \ce{_2^4He} + \ce{_{90}^{234}Th} + 2 \ce{_0^0\gamma} \nonumber \]
Virtually all of the nuclear reactions in this chapter also emit gamma rays, but for simplicity the gamma rays are generally not shown. Nuclear reactions produce a great deal more energy than chemical reactions. Chemical reactions release the difference between the chemical bond energy of the reactants and products, and the energies released have an order of magnitude of \(1 \times 10^3 \: \text{kJ/mol}\). Nuclear reactions release some of the binding energy and may convert tiny amounts of matter into energy. The energy released in a nuclear reaction has an order of magnitude of \(1 \times 10^{18} \: \text{kJ/mol}\). That means that nuclear changes involve almost one million times more energy per atom than chemical changes!
Note
Virtually all of the nuclear reactions in this chapter also emit gamma rays, but for simplicity the gamma rays are generally not shown.
The essential features of each reaction are shown in Figure 17.3.2
"Nuclear Accounting"
When writing nuclear equations, there are some general rules that will help you:
- The sum of the mass numbers (top numbers) on the reactant side equal the sum of the mass numbers on the product side.
- The atomic numbers (bottom numbers) on the two sides of the reaction will also be equal.
In the alpha decay of \(\ce{^{238}U}\) (Equation \(\ref{alpha1}\)), both atomic and mass numbers are conserved:
- mass number: \(238 = 4 + 234\)
- atomic number: \(92 = 2 + 90\)
Confirm that this equation is correctly balanced by adding up the reactants' and products' atomic and mass numbers. Also, note that because this was an alpha reaction, one of the products is the alpha particle, \(\ce{_2^4He}\).
Note that both the mass numbers and the atomic numbers add up properly for the beta decay of thorium-234 (Equation \(\ref{beta2}\)):
- mass number: \(234 = 0 + 234\)
- atomic number: \(90 = -1 + 91\)
The mass numbers of the original nucleus and the new nucleus are the same because a neutron has been lost, but a proton has been gained, and so the sum of protons plus neutrons remains the same. The atomic number in the process has been increased by one since the new nucleus has one more proton than the original nucleus. In this beta decay, a thorium-234 nucleus has one more proton than the original nucleus. In this beta decay, a thorium-234 nucleus has become a protactinium-234 nucleus. Protactinium-234 is also a beta emitter and produces uranium-234.
\[\ce{_{91}^{234}Pa} \rightarrow \ce{_{-1}^0e} + \ce{_{92}^{234}U} \label{nuke1} \]
Once again, the atomic number increases by one and the mass number remains the same; this confirms that the equation is correctly balanced.
What About Balancing Charge?
Both alpha and beta particles are charged, but nuclear reactions in Equations \(\ref{alpha1}\), \(\ref{beta2}\), and most of the other nuclear reactions above, are not balanced with respect to charge, as discussed when balancing redox reactions. When studying nuclear reactions in general, there is typically little information or concern about the chemical state of the radioactive isotopes, because the electrons from the electron cloud are not directly involved in the nuclear reaction (in contrast to chemical reactions).
So it is acceptable to ignore charge in balancing nuclear reactions, and concentrate on balancing mass and atomic numbers only.
Example \(\PageIndex{1}\)
Complete the following nuclear reaction by filling in the missing particle.
\[\ce{_{86}^{210}Rn} \rightarrow \ce{_2^4He} + ? \nonumber \]
Solution
This reaction is an alpha decay. We can solve this problem one of two ways:
Solution 1: When an atom gives off an alpha particle, its atomic number drops by 2 and its mass number drops by 4, leaving: \(\ce{_{84}^{206}Po}\). We know the symbol is \(\ce{Po}\), for polonium, because this is the element with 84 protons on the periodic table.
Solution 2: Remember that the mass numbers on each side must total up to the same amount. The same is true of the atomic numbers.
- Mass numbers: \(210 = 4 + ?\)
- Atomic numbers: \(86 = 2 + ?\)
We are left with \(\ce{_{84}^{206}Po}\).
Example \(\PageIndex{2}\)
Write each of the following nuclear reactions.
a) Carbon-14, used in carbon dating, decays by beta emission.
b) Uranium-238 decays by alpha emission.
Solution
a) Beta particles have the symbol \(\ce{_{-1}^0e}\). Emitting a beta particle causes the atomic number to increase by 1 and the mass number to not change. We get atomic numbers and symbols for elements using our periodic table. We are left with the following reaction:
\[\ce{_6^{14}C} \rightarrow \ce{_{-1}^0e} + \ce{_7^{14}N} \nonumber \]
b) Alpha particles have the symbol \(\ce{_2^4He}\). Emitting an alpha particle causes the atomic number to decrease by 2 and the mass number to decrease by 4. We are left with:
\[\ce{_{92}^{238}U} \rightarrow \ce{_2^4He} + \ce{_{90}^{234}Th} \nonumber \]



.svg.png?revision=1)