6.3: Thermochemistry
- Last updated
- Save as PDF
- Page ID
- 275979
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)In this section, we will discuss the use of experimentally-determined enthalpy changes to predict the enthalpy changes in chemical reactions and physical changes that are of interest to us. As noted in previous sections, any process that releases energy is called an exothermic process. For example, when methane or propane is oxidized by \(O_2\), the heat released causes the gas to expand, releasing heat and light, and doing work at the same time. If the process is carried out at constant pressure, this loss of energy represents a decrease in enthalpy (\(\Delta H < 0\)). An endothermic process absorbs energy, and in all cases, the energy is supplied from another source so that the enthalpy of the system increases (\(\Delta H > 0\)).
Standard Enthalpy Changes
In order to make the tabulated enthalpy data useful for scientific and engineering applications, there is a general agreement to report the enthalpy changes for a mole of a process at a set of standard conditions. For the vast majority of calculations, the accepted standard states, all at 1 bar pressure are:
- solids: pure solid
- liquids: pure liquid
- gases: pure gas
- solutes: 1 molal concentration \(\dfrac{1 \, mole \, solute}{kg \, solvent}\)
There is no specific temperature associated with standard conditions. You must specify the temperature for the process of interest. For example, the standard state for water at 298 K is pure liquid water at 1 bar and 298 K. The standard state for water at 398 K is pure gas at 1 bar and 398 K. The conventional temperature for standard state enthalpy values that are found in reference tables is 298.15 K, but there are certainly tables of enthalpy values for different temperatures.
The standard enthalpy change for a process, \(\Delta H^o\), is defined as the change in enthalpy when the pure, separate reactants, in their standard states, change to the pure, separate products, in their standard states, at a specified temperature. This definition holds for physical changes and for chemical reactions.
The standard enthalpy change for a process, \(\Delta H^o\), has the units of \(\dfrac{kJ}{mole \,process}\), where a process is a physical change or a chemical reaction. This is often a confusing concept because the word "process" is often left out of the units. As will become clear later, the presence or absence of the word "process" depends on the context of the statement or question.
The following are examples of thermochemical equations, each of which is a combination of a process and its corresponding change in standard enthalpy:
\(H_2O(l) \rightarrow H_2O(g)\) \(\Delta H^o = 44.016 \, kJ\)
\(H_2O(l) \rightarrow H_2O(g)\) \(\Delta H^o = 40.656 \, kJ \, (373K)\)
\(2H_2(g) + O_2(g) \rightarrow 2H_2O(l)\) \(\Delta H^o = -571.66 \, kJ\)
The reactions might more clearly be written as
\( 44.016 \, kJ \, + \, H_2O(l) \rightarrow H_2O(g)\)
\( 40.656 \, kJ \, + \, H_2O(l) \rightarrow H_2O(g) \, @ (373K)\)
\(2H_2(g) + O_2(g) \rightarrow 2H_2O(l) \, + \, 571.66 \, kJ\)
Physical Changes
When a pure liquid vaporizes, or when a solid changes from one polymorph to another, a change in state occurs. These changes in state involve changes in enthalpy that are classified as enthalpies of transition. It is common practice to list standard enthalpies of transition as the enthalpy change per 1 mole of particles undergoing the transition at 1 bar pressure. For example, the standard enthalpy of fusion (\(\Delta H^o_{fus}\)) for 1 mole of benzene at 278.6 K is written as
\(C_6H_6(s) \rightarrow C_6H_6(l)\)
with
\(\Delta H^o_{fus} = 10.59 \, \dfrac{kJ}{mole} \, (278.6 K)\)
Chemical Changes
A chemical change can be thought of as a process in which bonds between atoms in existing substances are broken and these atoms rearrange and/or reorganize to form the new bonds of different substances. To describe the enthalpy change of such a process it is common practice to list the standard enthalpy of reaction, \(\Delta H^o_r\) which has the units of \(\dfrac{kJ}{mole \, reaction}\).
\(3H_2(g) \, + \, N_2(g) \, \rightarrow 2NH_3(g)\)
with
\(\Delta H^o_r = -92.22 \dfrac{kJ}{mole}\)
is interpreted as 92.22 kJ of heat are given off per every 3 moles of \(H_2\) consumed, every 1 mole of \(N_2\) consumed, and every 2 moles of \(NH_3\) produced.
A Few Rules
At 298 K, the combustion of 1.0 mole hydrogen with 0.5 moles of oxygen to form 1.0 mole of H_2O releases 285.8 kJ of energy. We represent the reaction:
\(\mathrm{H_{2\large{(g)}} + \dfrac{1}{2} O_2 \rightarrow H_2O_{\large{(l)}}}, \hspace{20px} \Delta H^o_r = \mathrm{-285.8\: kJ/mole}\)
For the reverse reaction, 285.8 kJ/mol is required, thus the sign for \(\Delta H^o_r\) changes
\(\mathrm{H_2O_{\large{(l)}} \rightarrow H_{2\large{(g)}} + \dfrac{1}{2} O_2}, \hspace{20px} \Delta H^o_r = \mathrm{+285.8\: kJ/mole}\)
It is also true that the amount of energy released in a chemical reaction is related to the amount of reactants. For example, when the amount of reactants is doubled, so is the amount of energy released.
\(\mathrm{2 H_{2\large{(g)}} + O_2 \rightarrow 2 H_2O_{\large{(l)}}}, \hspace{20px} \Delta H^o_r = \mathrm{-571.66\: kJ/mole}\)
Example \(\PageIndex{1}\): Standard Enthalpy of Reaction
The standard enthalpy for the combustion of methane is -890. kJ per mole,
\(CH_4\, (g) + 2 O_2\, (g) \rightarrow CO_2\, (g) + 2 H_2O \, (g) \hspace{20px} \Delta H^o_r = \, -890.\, kJ\)
Calculate the standard enthalpy change when 3.50 moles of oxygen are consumed during the conversion of methane to the gaseous products at 298 K.
Solution
When 2.00 moles of \(O_2\), at 298 K and 1.00 bar, reacts with \(CH_4\) according to the given equation, the standard enthalpy change is 890. kJ. Thus, the standard change of enthalpy when 3.50 moles of \(O_2\) are used is
\(\Delta H^o_r = 3.50 \, moles \, O_2 \times \dfrac{890.\, kJ}{2.00 \, mole \, O_2} = - 1560 \, kJ \).
Exercise \(\PageIndex{1}\)
Calculate the standard change in enthalpy when 75.0 grams of Al are completely used up in the following reaction:
\( 2Al(s) + Fe_2O_3(s) \rightarrow 2Fe(s) + Al_2O_3 + 850 kJ\)
Answer: \(\Delta H^o_r\) = -1180 kJ
Standard Heats of Formation
Another way to look at \(\Delta H^o_r\) is to state that
\[\Delta H^o_r = \sum_{products} \, vH^o_m \, - \, \sum_{reactants} \, vH^o_m \label{2.3.1}\]
where \(v\) is the stoichiometric coefficient of each substance with the units of \(\dfrac{moles \, substance}{moles \, reaction}\).
Equation \(\ref{2.3.1}\) is of no use for practical applications because the values of absolute \(H^o_m\) are unknown. This inconvenience can be overcome by creating a self-consistent system in which definitions that are demonstrably incorrect can nevertheless be used to calculate \(\Delta H^o_m\) values known as standard enthalpies of formation, \(\Delta H^o_f\). By definition, the \(\Delta H^o_f\) of a substance is the enthalpy change the accompanies the formation of exactly 1 mole of the substance when the starting materials are the pure elements in their most stable form at the given set of conditions. The demonstrably incorrect aspect is that the \(\Delta H^o_f\) of pure elements in their most stable allotrope under the given conditions is defined to be 0 \(\dfrac{kJ}{mole}\), a tactic that will be explained later. A similar definition, instituted to allow for the determination of \(\Delta H^o_f\) for ions in aqueous solutions, is that \(\Delta H^o_f\) = 0 kJ for the hydrogen ion, H+ (aq).
For example, at 298 K, the combustion of 1.0 mole hydrogen with 0.5 moles of oxygen to form 1.0 mole of \(H_2O\) releases 286 kJ of energy. We represent the reaction:
\(\mathrm{H_{2\large{(g)}} + \dfrac{1}{2} O_2 \rightarrow H_2O_{\large{(l)}}}, \hspace{20px} \Delta H^o_f = \mathrm{-286\: kJ/mol}\)
The following table shows several reactions that fit into the category of standard enthalpy of formation reactions:
\(\begin{align}
&\mathrm{Mg_{\large{(s)}} + \dfrac{1}{8}S_{8\large{(s)}} \rightarrow MgS_{\large{(s)}}}
&&\Delta H^\circ_{\mathrm f} = \mathrm{-598\: kJ/mol}\\
&\mathrm{P_{\large{(s)}} + \dfrac{3}{2} Cl_{2\large{(g)}} \rightarrow PCl_{3\large{(g)}}}
&&\Delta H^\circ_{\mathrm f} = \mathrm{-320\: kJ/mol}\\
&\mathrm{P_{\large{(s)}} + \dfrac{5}{2} Cl_{2\large{(g)}} \rightarrow PCl_{5\large{(g)}}}
&&\Delta H^\circ_{\mathrm f} = \mathrm{- 440\: kJ/mol}\\
&\mathrm{H_{2\large{(g)}} + \dfrac{1}{2} O_{2\large{(g)}} \rightarrow H_2O_{\large{(l)}}}
&&\Delta H^\circ_{\mathrm f} = \mathrm{-286\: kJ/mol}\\
&\mathrm{\dfrac{1}{2}N_{2\large{(g)}} + O_{2\large{(g)}} \rightarrow NO_{2\large{(g)}}}
&&\Delta H^\circ_{\mathrm f} = \mathrm{+ 34\: kJ/mol}\\
&\mathrm{Cu_{\large{(s)}} + \dfrac{1}{2} O_{2\large{(g)}} \rightarrow CuO_{\large{(s)}}}
&&\Delta H^\circ_{\mathrm f} = \mathrm{-157\: kJ/mol}\\
&\mathrm{Mg_{\large{(s)}} + \dfrac{1}{2} O_{2\large{(g)}} \rightarrow MgO_{\large{(s)}}}
&&\Delta H^\circ_{\mathrm f} = \mathrm{-602\: kJ/mol}\\
&\mathrm{C_{\large{(graphite)}} + O_{2\large{(g)}} \rightarrow CO_{2\large{(g)}}}
&&\Delta H^\circ_{\mathrm f} = \mathrm{-394\: kJ/mol}\\
&\mathrm{C_{\large{(graphite)}} + 4 H_{2\large{(g)}} \rightarrow CH_{4\large{(g)}}}
&&\Delta H^\circ_{\mathrm f} = \mathrm{-75\: kJ/mol}
\end{align}\)
In all the above equations of reaction, the right hand side has only one product and its coefficient is 1. To obtain a balanced equation, it is often necessary to use fractional coefficients for the pure element reactants, which is allowed because all of the reactions are taking place on the molar scale. (Thermodynamics is a study of macroscopic systems.) Because all standard enthalpy of formation reactions are, by definition, the formation of 1 mole of a pure substance from its component elements in their most stable form under the reaction conditions, we often do not write out the entire equation, but instead simply write
\(\Delta H^o_f \, MgS(s) = -598\, \dfrac{kJ}{mole \, MgS}\)
Note
The use of \(\Delta H^o_f\) values to calculate \(\Delta H^o_r\) values is made possible by assuming that any chemical reaction can be broken down into two distinct , hypothetical steps:
Step 1) All of the reactants decompose ("unform") to produce the pure elements of which they are composed.
Step 2) All of the pure elements created in Step 1 react to form the products of the overall reaction.
If these hypothetical steps are assumed to occur, it is perfectly legitimate (although absolutely incorrect) to assign all of the pure elements a \(\Delta H^o_f\) = 0 kJ. For example, even though we know that 436 kJ is released when 2 moles of H atoms react to form 1 mole of H2 , we can proceed with the erroneous assumption that the \(\Delta H^o_f\) of \(H_2 \) = 0 kJ because the \(\Delta H^o_f\) of every hydrogen-containing compound will incorporate this erroneous value of \(\Delta H^0_f\) of \(H_2 \). Thus, the \(\Delta H^o_f\) of \(H_2O\) incorporates not only the enthalpy change associated with the formation of the bonds in \(H_2O\), but also the enthalpy change associated with the breaking of bonds in H2 and in O2.
When calculating both the change in enthalpy for Step 1 and the change in enthalpy for Step 2 of any reaction, the incorrect assignment of a value of 0 kJ will be canceled out as we first "unform" reactants and then form products. (Two wrongs make a right in this case!) The following calculation will show this point:
Calculate the \(\Delta H^o_r\) for the reaction \(CH_4 \, (g) \, + \, 2 \, O_2 \, (g) \rightarrow 2 \, H_2O \, (g) \, + \, CO_2 \, (g)\), given the data: \(\Delta H^o_f\) \(H_2O\) = -286 \(\dfrac{kJ}{mole}\); \(\Delta H^o_f\) \(CO_2\) = -394 \(\dfrac{kJ}{mole}\); \(\Delta H^o_f\) \(CH_4\) = -75 \(\dfrac{kJ}{mole}\).
Step 1: Unforming reactants \(CH_4 \, (g) \, + \, 2 \, O_2 \, (g) \rightarrow C \, (graphite) \, + \, 2 H_2 \, (g) \, + \, 2 \, O_2 \, (g) \)
Step 2: Forming products \(C \, (graphite) \, + \, 2 H_2 \, (g) \, + \, 2 \, O_2 \, (g) \rightarrow 2\, H_2O \, (g) \, + \, CO_2 \, (g) \)
It is not possible to obtain a thermodynamically precise value of \(\Delta H^o_f)\ for a substance by adding up the contribution of each of the bonds in the substance. For instance, the \(\Delta H^o_f)\ for CH4 can not be precisely approximated by adding up the energy released by the formation of 4 C - H bonds. The attempts fails because the \(\Delta H\) of a C - H bond differs from compound to compound, and even within a compound. (For instance, the energy needed to break the first C - H bond in CH4 is different from the energy needed to break the second C - H bond in the remaining CH3 particle.) Molecular modeling with computers has improved the approximated bond energies, but experimentation is still the most reliable technique to determine precise values for \(\Delta H^o_f)\.
Given the concept of \(\Delta H^o_f\), it is possible to re-write equation \(\ref{2.3.1}\) as
\[\Delta H^o_r = \sum_{products} \, v\Delta H^o_f \, - \, \sum_{reactants} \, v\Delta H^o_f \label{2.3.11}\]
in which we use the standard enthalpies of formation to calculate the standard enthalpy of reaction.
To demonstrate the use of tabulated ΔHοf values, we will use them to calculate ΔHrxn for the combustion of glucose:
\[ C_{6}H_{12}O_{6} \left ( s \right ) + O_{2}\left ( g \right ) \rightarrow CO_{2}\left ( g \right ) + 6H_{2}O\left ( l \right ) \label{2.3.12} \]
Using Equation \(\ref{2.3.11}\), we write
\[ \Delta H_{r}^{o} =\left \{ 6\Delta H_{f}^{o}\left [ CO_{2}\left ( g \right ) \right ] + 6\Delta H_{f}^{o}\left [ H_{2}O\left ( g \right ) \right ] \right \} - \left \{ 6\Delta H_{f}^{o}\left [ C_{6}H_{12}O_{6}\left ( s \right ) \right ] + 6\Delta H_{f}^{o}\left [ O_{2}\left ( g \right ) \right ] \right \} \label{2.3.13} \]
The relevant ΔHοf values are ΔHοf [CO2(g)] = -393.5 kJ/mol, ΔHοf [H2O(l)] = -285.8 kJ/mol, and ΔHοf [C6H12O6(s)] = -1273.3 kJ/mol. Because O2(g) is a pure element in its standard state, ΔHοf [O2(g)] = 0 kJ/mol. Inserting these values into Equation \(\ref{2.3.13}\) and changing the subscript to indicate that this is a combustion reaction, we obtain
\[ \begin{matrix} \Delta H_{comb}^{o} = \left [ 6\left ( -393.5 \; kJ/mol \right ) + 6 \left ( -285.8 \; kJ/mol \right ) \right ] \\ - \left [-1273.3 + 6\left ( 0 \; kJ\;mol \right ) \right ] = -2802.5 \; kJ/mol \end{matrix} \label{2.3.14} \]
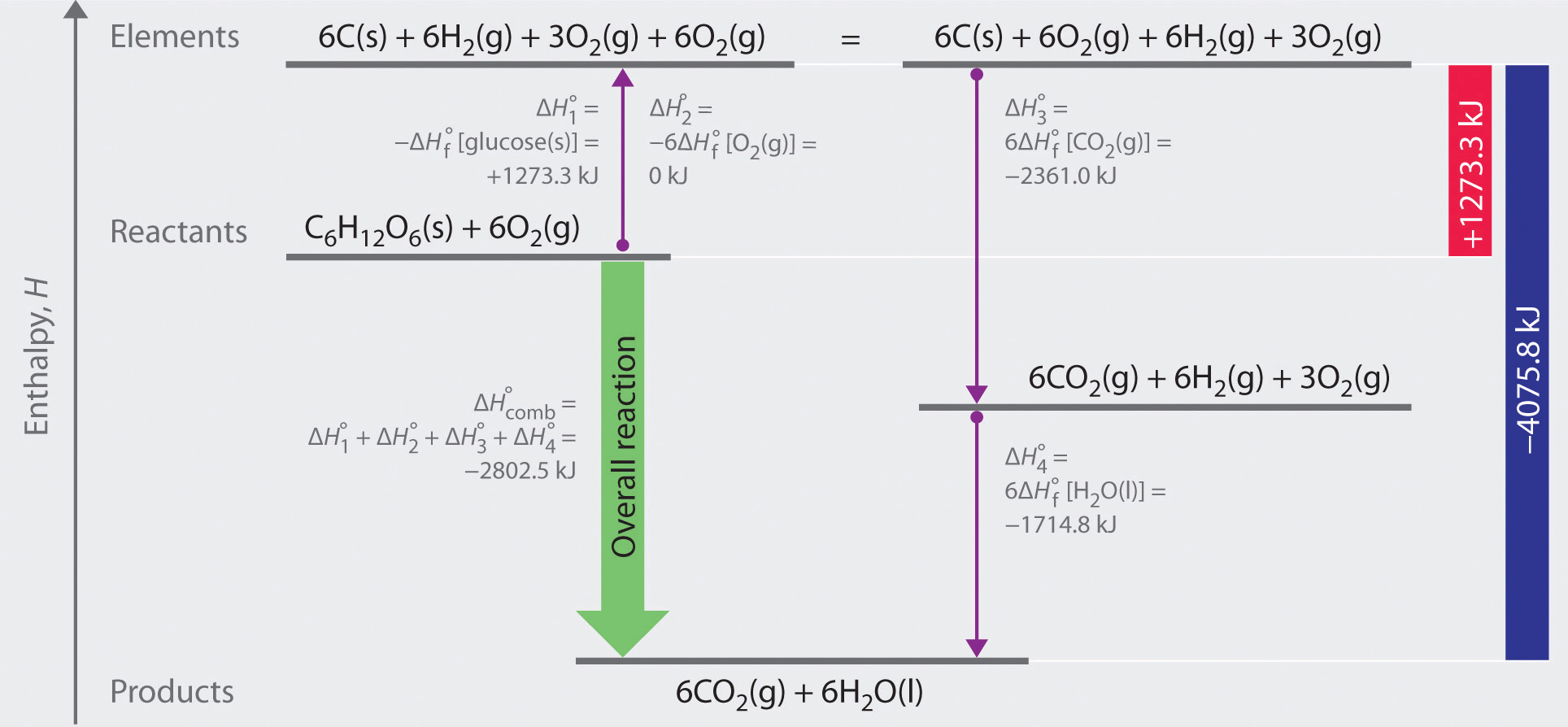
As illustrated in Figure \(\PageIndex{1}\), we can use Equation \(\ref{2.3.11}\) to calculate ΔHοf for glucose because enthalpy is a state function. The figure shows two pathways from reactants (middle left) to products (bottom). The more direct pathway is the downward green arrow labeled ΔHοcomb The alternative hypothetical pathway consists of four separate reactions that convert the reactants to the elements in their standard states (upward purple arrow at left) and then convert the elements into the desired products (downward purple arrows at right). The reactions that convert the reactants to the elements are the reverse of the equations that define the ΔHοf values of the reactants. Consequently, the enthalpy changes are
\[ \begin{matrix} \Delta H_{1}^{o} = \Delta H_{f}^{o} \left [ glucose \left ( s \right ) \right ] = -1 \; \cancel{mol \; glucose}\left ( \frac{1273.3 \; kJ}{1 \; \cancel{mol \; glucose}} \right ) = +1273.3 \; kJ \\ \Delta H_{2}^{o} = 6 \Delta H_{f}^{o} \left [ O_{2} \left ( g \right ) \right ] = 6 \; \cancel{mol \; O_{2}}\left ( \frac{0 \; kJ}{1 \; \cancel{mol \; O_{2}}} \right ) = 0 \; kJ \end{matrix} \label{2.3.15} \]
(Recall that when we reverse a reaction, we must also reverse the sign of the accompanying enthalpy change.) The overall enthalpy change for conversion of the reactants (1 mol of glucose and 6 mol of O2) to the elements is therefore +1273.3 kJ.
Figure \(\PageIndex{1}\): A Thermochemical Cycle for the Combustion of Glucose. Two hypothetical pathways are shown from the reactants to the products. The green arrow labeled ΔHοcomb indicates the combustion reaction. Alternatively, we could first convert the reactants to the elements via the reverse of the equations that define their standard enthalpies of formation (the upward arrow, labeled ΔHο1 and ΔHο2 ). Then we could convert the elements to the products via the equations used to define their standard enthalpies of formation (the downward arrows, labeled ΔHο3 and ΔHο4 ). Because enthalpy is a state function, ΔHοcomb is equal to the sum of the enthalpy changes ΔHο1 + ΔHο2 + ΔHο3 + ΔHο4.
The reactions that convert the elements to final products (downward purple arrows in Figure 2.3.1) are identical to those used to define the ΔHοf values of the products. Consequently, the enthalpy changes are
\[ \begin{matrix} \Delta H_{3}^{o} = \Delta H_{f}^{o} \left [ CO_{2} \left ( g \right ) \right ] = 6 \; \cancel{mol \; CO_{2}}\left ( \dfrac{393.5 \; kJ}{1 \; \cancel{mol \; CO_{2}}} \right ) = -2361.0 \; kJ \\ \Delta H_{4}^{o} = 6 \Delta H_{f}^{o} \left [ H_{2}O \left ( l \right ) \right ] = 6 \; \cancel{mol \; H_{2}O}\left ( \dfrac{-285.8 \; kJ}{1 \; \cancel{mol \; H_{2}O}} \right ) = -1714.8 \; kJ \end{matrix} \]
The overall enthalpy change for the conversion of the elements to products (6 mol of carbon dioxide and 6 mol of liquid water) is therefore −4075.8 kJ. Because enthalpy is a state function, the difference in enthalpy between an initial state and a final state can be computed using any pathway that connects the two. Thus the enthalpy change for the combustion of glucose to carbon dioxide and water is the sum of the enthalpy changes for the conversion of glucose and oxygen to the elements (+1273.3 kJ) and for the conversion of the elements to carbon dioxide and water (−4075.8 kJ):
\[ \Delta H_{comb}^{o} = +1273.3 \; kJ +\left ( -4075.8 \; kJ \right ) = -2802.5 \; kJ \label{2.3.16} \]
This is the same result we obtained using the “products minus reactants” rule (Equation \(\ref{2.3.11}\)) and ΔHοf values. The two results must be the same because Equation \(\ref{2.3.16}\) is just a more compact way of describing the thermochemical cycle shown in Figure \(\ref{2.3.1}\).
Example \(\PageIndex{2}\)
Long-chain fatty acids such as palmitic acid [CH3(CH2)14CO2H] are one of the two major sources of energy in our diet (ΔHοf =−891.5 kJ/mol). Use the appropriate data to calculate ΔHοr for the combustion of 1 mole of palmitic acid.
Given: compound and ΔHοf values
Asked for: ΔHοr per mole
Strategy:
- After writing the balanced chemical equation for the reaction, use Equation \(\ref{2.3.11}\) and the ΔHοf values for H2O(l) and CO2 (g) to calculate ΔHοr, the energy released by the combustion of 1 mol of palmitic acid.
Solution:
A To determine the energy released by the combustion of palmitic acid, we need to calculate its ΔHοr. As always, the first requirement is a balanced chemical equation:
\[C_{16}H_{32}O_{2(s)} + 23O_{2(g)} \rightarrow 16CO_{2(g)} + 16H_2O_{(l)}\]
Using Equation \(\ref{2.3.11}\) with ΔHοf values (and omitting the physical states of the reactants and products to save space) gives
\( \Delta H_{r}^{o} = \sum m \Delta {H^o}_f\left( {products} \right) - \sum n \Delta {H^o}_f\left( {reactants} \right) \)
\( = \left [ 16\left ( -393.5 \; kJ/mol \; CO_{2} \right ) + 16\left ( -285.8 \; kJ/mol \; H_{2}O \; \right ) \right ] \)
\( - \left [ -891.5 \; kJ/mol \; C_{16}H_{32}O_{2} + 23\left ( 0 \; kJ/mol \; O_{2} \; \right ) \right ] \)
\( = -9977.3 \; kJ/mol \)
This is the energy released by the combustion of 1 mol of palmitic acid.
Exercise \(\PageIndex{2}\)
Calculate ΔHοr for the water–gas shift reaction, which is used industrially on an enormous scale to obtain H2(g):
\( \begin{pmatrix}
CO\left ( g \right )+H_{2}O\left ( g \right )\rightarrow CO_{2} \left ( g \right )+H_{2}\left ( g \right ) \\
water-gas \; shift \; reaction
\end{pmatrix} \)
Answer:
−41.2 kJ/mol
Hess's Law
Hess's Law of Constant Heat Summation (or just Hess's Law) states that regardless of the multiple stages or steps of a reaction, the total enthalpy change for the reaction is the sum of all changes. This law is a manifestation of enthalpy as a state function, which allows us to calculate the overall change in enthalpy by simply summing up the changes for each step of the way, until the desired product is formed. All steps have to proceed under the same reaction conditions and the equations for the individual steps must balance out. The principle underlying Hess's law does not just apply to enthalpy and can be used to calculate other state functions like changes in Gibbs' free energy and entropy.
Definition: Hess's Law
The heat of any reaction \(\Delta{H^°_r}\) for a specific reaction is equal to the sum of the heats of reaction for any set of reactions which in sum are equivalent to the overall reaction:
Application
Hydrogen gas, which is of potential interest nationally as a clean fuel, can be generated by the reaction of carbon (coal) and water:
\[C_{(s)} + 2 H_2O_{(g)} \rightarrow CO_{2\, (g)} + 2 H_{2\, (g)} \label{2.3.19}\]
Calorimetry reveals that this reaction requires the input of 90.1 kJ of heat for every mole of \(C_{(s)}\) consumed. By convention, when heat is absorbed during a reaction, we consider the quantity of heat to be a positive number: in chemical terms, \(q > 0\) for an endothermic reaction. When heat is evolved, the reaction is exothermic and \(q < 0\) by convention.
It is interesting to ask where this input energy goes when the reaction occurs. One way to answer this question is to consider the fact that the reaction converts one fuel, \(C_{(s)}\), into another, \(H_{2(g)}\). To compare the energy available in each fuel, we can measure the heat evolved in the combustion of each fuel with one mole of oxygen gas. We observe that
\[C_{(s)}+O_{2(g)} \rightarrow CO_{2(g)} \label{2.3.20}\]
produces \(393.5\, kJ\) for one mole of carbon burned; hence \(q=-393.5\, kJ\). The reaction
\[2 H_{2(g)} + O_{2(g)} \rightarrow 2 H_2O_{(g)} \label{2.3.21}\]
produces 483.6 kJ for two moles of hydrogen gas burned, so q=-483.6 kJ. It is evident that more energy is available from combustion of the hydrogen fuel than from combustion of the carbon fuel, so it is not surprising that conversion of the carbon fuel to hydrogen fuel requires the input of energy. Of considerable importance is the observation that the heat input in equation \(\ref{2.3.19}\), 90.1 kJ, is exactly equal to the difference between the heat evolved, -393.5 kJ, in the combustion of carbon and the heat evolved, -483.6 kJ, in the combustion of hydrogen. This is not a coincidence: if we take the combustion of carbon and add to it the reverse of the combustion of hydrogen, we get
\(C_{(s)}+O_{2(g)} \rightarrow CO_{2(g)}\)
\(2 H_2O_{(g)} \rightarrow 2 H_{2(g)} + O_{2(g)}\)
\[C_{(s)} + O_{2(g)} + 2 H_2O_{(g)} \rightarrow CO_{2(g)} + 2 H_{2(g)} + O_{2(g)} \label{2.3.22}\]
Canceling the \(O_{2(g)}\) from both sides, since it is net neither a reactant nor product, equation \(\ref{2.3.22}\) is equivalent to equation \(\ref{2.3.19}\). Thus, taking the combustion of carbon and "subtracting" the combustion of hydrogen (or more accurately, adding the reverse of the combustion of hydrogen) yields equation \(\ref{2.3.19}\). And, the heat of the combustion of carbon minus the heat of the combustion of hydrogen equals the heat of equation \(\ref{2.3.19}\). By studying many chemical reactions in this way, we discover that this result, known as Hess's Law, is general.
Why it works
A pictorial view of Hess's Law as applied to the heat of equation \(\ref{2.3.19}\) is illustrative. In figure 2.3.1, the reactants C(s) + 2 H2O(g) are placed together in a box, representing the state of the materials involved in the reaction prior to the reaction. The products CO2(g) + 2 H2(g) are placed together in a second box representing the state of the materials involved after the reaction. The reaction arrow connecting these boxes is labeled with the heat of this reaction. Now we take these same materials and place them in a third box containing C(s), O2(g), and 2 H2(g). This box is connected to the reactant and product boxes with reaction arrows, labeled by the heats of reaction in equation \(\ref{2.3.20}\) and equation \(\ref{2.3.21}\).
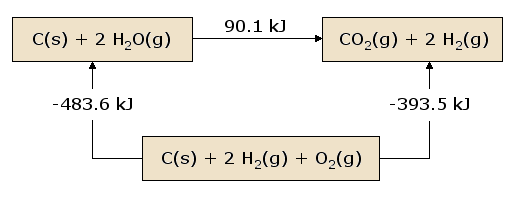
Figure 1: A Pictorial View of Hess's Law.
This picture of Hess's Law reveals that the heat of reaction along the "path" directly connecting the reactant state to the product state is exactly equal to the total heat of reaction along the alternative "path" connecting reactants to products via the intermediate state containing \(C_{(s)}\), \(O_{2(g)}\), and 2 \(H_{2(g)}\). A consequence of our observation of Hess's Law is therefore that the net heat evolved or absorbed during a reaction is independent of the path connecting the reactant to product (this statement is again subject to our restriction that all reactions in the alternative path must occur under constant pressure conditions).
Extensive tables of ΔH°r values have been compiled that allow us to calculate the heat of reaction for any reaction of interest, even including hypothetical reactions which may be difficult to perform or impossibly slow to react. The following reactions are examples of such ΔH°r reactions:
\(\begin{align}
&\mathrm{2 H_{\large{(g)}} \rightarrow H_{2\large{(g)}}} &&\Delta H^\circ = \mathrm{-436\: kJ/mol}\\
&\mathrm{2 O_{\large{(g)}} \rightarrow O_{2\large{(g)}}} &&\Delta H^\circ = \mathrm{-498\: kJ/mol}\\
&\mathrm{H_2O_{\large{(l)}} \rightarrow H_2O_{\large{(g)}}} &&\Delta H^\circ = \mathrm{44\: kJ/mol\: at\: 298\: K}\\
&\mathrm{H_2O_{\large{(l)}} \rightarrow H_2O_{\large{(g)}}} &&\Delta H = \mathrm{41\: kJ/mol\: at\: 373\: K,\: \textrm{non-standard}\: condition}\\
&\mathrm{Mg_{\large{(s)}} + S_{\large{(s)}} \rightarrow MgS_{\large{(s)}}} &&\Delta H^\circ = \mathrm{-598\: kJ/mol}\\
&\mathrm{2 H_{\large{(g)}} + O_{\large{(g)}} \rightarrow H_2O_{\large{(g)}}} &&\Delta H^\circ =\mathrm{-847\: kJ/mol}\\
&\mathrm{Cu_{\large{(s)}} + \dfrac{1}{2}O_{2\large{(g)}} \rightarrow CuO_{\large{(s)}}} &&\Delta H^\circ = \mathrm{-157\: kJ/mol}\\
&\mathrm{\dfrac{1}{2}N_{2\large{(g)}} + O_{2\large{(g)}} \rightarrow NO_{2\large{(g)}}} &&\Delta H^\circ = \mathrm{34\: kJ/mol}\\
&\mathrm{Mg_{\large{(s)}} + \dfrac{1}{2}O_{2\large{(g)}} \rightarrow MgO_{\large{(s)}}} &&\Delta H^\circ = \mathrm{-602\: kJ/mol}\\
&\mathrm{2 P_{\large{(s)}} + 3 Cl_{2\large{(g)}} \rightarrow 2 PCl_{3\large{(s)}}} &&\Delta H^\circ = \mathrm{-640\: kJ/mol}\\
&\mathrm{2 P_{\large{(s)}} + 5 Cl_{2\large{(g)}} \rightarrow 2 PCl_{5\large{(s)}}} &&\Delta H^\circ = \mathrm{-880\: kJ/mol}\\
&\mathrm{C_{\large{(graphite)}} + 2 O_{\large{(g)}} \rightarrow CO_{2\large{(g)}}} &&\Delta H^\circ = \mathrm{-643\: kJ/mol}\\
&\mathrm{C_{\large{(graphite)}} + O_{2\large{(g)}} \rightarrow CO_{2\large{(g)}}} &&\Delta H^\circ = \mathrm{-394\: kJ/mol}\\
&\mathrm{C_{\large{(graphite)}} + 2 H_{2\large{(g)}} \rightarrow CH_{4\large{(g)}}} &&\Delta H^\circ = \mathrm{-75\: kJ/mol}\\
&\mathrm{2 Al_{\large{(s)}} + Fe_2O_{3\large{(s)}} \rightarrow Al_2O_{3\large{(s)}} + 2Fe_{\large{(s)}}} &&\Delta H^\circ = \mathrm{-850\: kJ/mol}
\end{align}\)
Example \(\PageIndex{3}\): Solving for Standard Enthalpy of Reaction Using Hess's Law
QUESTION
Calculate the standard enthalpy of combustion of the transition of C(s, graphite) → C(s, diamond), given
\[\ce{C(s, graphite) + O_2 -> CO_2} \;\;\; ΔH^o_r = -393.5 kJ/mol\]
\[\ce{CO_2 -> C_{(s, diamond)} + O_2}\;\;\; ΔH^o_r = + 395.41 kJ/mol\]
Solution
- Find appropriate reactions and their standard enthalpy reaction
- Flip reactions and/or multiply reactions, if necessary, so that the combination of reactions results in the desired overall reaction
- Change the sign and/or magnitude of the \(\Delta H^o_r\) values of the combined reactions, based on how the combined reactions were manipulated in Step 2
- Sum up the individual steps and sum up the individual \(\Delta H^o_r\) values to obtain the \(\Delta H^o_r\) value of the desired reaction.
Answer
In this case, there is no need to flip an equation around because it is possible to cancel out terms as the reactions are given. What is left is canceling out the O2 and the CO2 species, writing the overall reaction and then summing the two reaction enthalpies together.
C(s, graphite) + O2 → CO2
CO2 → C(s, diamond) + O2
\(C_{(s, graphite)} \rightarrow C_{(s, diamond) }\)
Adding the enthalpies gives (-393.5 kJ/mol + 395.41 kJ/mol) = +1.91 kJ/mol. Since the \(\Delta H^o_r\) is positive, the reaction is endothermic.
Exercise \(\PageIndex{3}\): Steam Reforming
Steam reforming is a method for producing hydrogen, carbon monoxide, or other useful products from hydrocarbon fuels such as natural gas. Use Hess’s Law to calculate the following enthalpy of reaction of the major process of steam reforming:
\[CH_{4(g)} + H_2O_{(g)} \rightleftharpoons CO_{(g)} + 3H_{2(g)} \label{E1}\]
Given the separate reactions of carbon dioxide and hydrogen gas and methane decomposition;
\[CO_{(g)} + H_{2(g)} \rightarrow C_{(graphite)} + H_2O_{(g)} \;\;\; ΔH° = -131.3\; kJ \label{E2}\]
\[C_{(graphite)} + 2H_{2(g)} \rightarrow CH_{4(g)} \;\;\; ΔH^° = -74.8\; kJ \label{E3}\]
\[CH_{4(g)} + H_2O \rightarrow CO + 3H_2 \;\;\; ΔH^° = +74.8 \;kJ + 131.3\; kJ\]
Answer
\(CH_{4(g)} + H_2O \rightarrow CO + 3H_2 \;\;\; ΔH^°_r = 201.1\; kJ\)
Hence, it is not surprising that this reforming reactions takes place at high temperatures.
The Temperature Dependence of \(\Delta H^o_r\)
For educational purposes most textbooks list thermodynamic values such as \(\Delta H^o_f\) and \(\Delta H^o_r\) for processes occurring at 298 K. It is obvious that not all reactions occur at this temperature. More advanced texts and reference books may have tables of thermodynamic data at temperatures other than 298 K, but they do not have values for all temperatures. Kirchhoff's Law can be used to accurately estimate the standard enthalpy of reaction at an elevated temperature if the standard enthalpy of reaction and the constant pressure heat capacity are known.
Kirchhoff's law is
\[\Delta H^o_r(T_2) = \Delta H^o_r(T_1) + \int \Delta_r C^o_P \, dT \label{2.3.44}\]
where T2 > T1, the CP values of the products and reactants do not change much over the temperature range from T1 to T2, and \(\Delta_r C^o_P\) is the difference between the constant pressure molar heat capacities of the products and reactants, weighted by their stoichiometric coefficients:
\[\Delta_r C^o_{P,m} = \sum_{products} \, vC^o_{P,m} \, - \, \sum_{reactants} \, vC^o_{P,m} \label{2.3.45}\]
where \(v\) is the stoichiometric coefficient of each substance.
If \(\Delta_r C^o_{P,m}\) remains constant over the temperature range, then equation \(\ref{2.3.44}\) becomes
\[\Delta H^o_r(T_2) = \Delta H^o_r(T_1) + (T_2 - T_1)\Delta_r C^o_{P,m}\label{2.3.46}\]
Example \(\PageIndex{4}\):
The \(\Delta H^o_f\) for H2O (l) at 298 K is -286 \(\dfrac{kJ}{mole}\). Estimate the value of \(\Delta H^o_f\) for H2O (l) at 350 K. The constant pressure molar heat capacities of the reactants and products are: H2O (l) = 75.29 \(\dfrac{J}{K·mole}\); H2 (g) = 28.84 \(\dfrac{J}{K·mole}\); O2 (g) = 29.37 \(\dfrac{J}{K·mole}\). It is assumed that these values do not change over the given temperature range.
Given: \(\Delta H^o_f\) H2O (l) at 298 and \(C^o_{P,m}\) values for the reactants and products.
Asked for: \(\Delta H^o_f\) H2O (l) at 350 K
Strategy: Use equation \(\ref{2.3.45}\) to determine the \(\Delta_r C^o_{P,m}\) for the reaction, then substitute this value into equation \(\ref{2.3.46}\).
Solution: The reaction is \(H_2 (g) \, + \, \dfrac{1}{2} O_2 (g) \, \rightarrow H_2O (l) \)
Thus, \(\Delta_r C^o_{P,m} = C^o_{P,m} (H_2O, l) - \left( C^o_{P,m} (H_2, g) + \dfrac{1}{2} C^o_{P,m} (O_2, g) \right) \)
and \(\Delta_r C^o_{P,m} = 75.29 \dfrac{J}{K·mole} - \left( 28.84 \dfrac{J}{K·mole} + \dfrac{1}{2} 29.37 \dfrac{J}{K·mole}\right) = 31.77 \dfrac{J}{K·mole} = 0.03177 \dfrac{kJ}{K·mole} \)
Then, \(\Delta H^o_f (H_2O (l), 350 K) = -286 \dfrac{kJ}{mole} + (350 K - 298 K) \left( 0.03177 \dfrac{J}{K·mole} \right) = -284 \dfrac{kJ}{mole} \)
This is not a large change, but it may be significant depending what you are trying to measure.
Exercise \(\PageIndex{4}\)
The \(\Delta H^o_f\) for H2O (g) at 298 K is -241.8 \(\dfrac{kJ}{mole}\). Estimate the value of \(\Delta H^o_f\) for H2O (l) at 400 K. The constant pressure molar heat capacities of the reactants and products are: H2O (g) = 33.58 \(\dfrac{J}{K·mole}\); H2 (g) = 28.84 \(\dfrac{J}{K·mole}\); O2 (g) = 29.37 \(\dfrac{J}{K·mole}\). It is assumed that these values do not change over the given temperature range.
Answer: -242.8 kJ/mole
References
- Atkins, Peter and Julio de Paula. Physical Chemistry for the Life Sciences. New York: Oxford University Press, 2006.
- Petrucci, et al. General Chemistry: Principles & Modern Applications: AIE (Hardcover). Upper Saddle River: Pearson/Prentice Hall, 2007.
- Senese, Fred. What are extensive and intensive properties? General Chemistry Online. 1997-2005.
 antoine.frostburg.edu/chem/senese/101/matter/faq/extensive-intensive.shtml
antoine.frostburg.edu/chem/senese/101/matter/faq/extensive-intensive.shtml - Canagaratna, Sebastian G."Intensive and extensive: Underused concepts." J. Chem. Educ. 1992: 69, 957.
Contributors and Attributions
Chung (Peter) Chieh (Professor Emeritus, Chemistry @ University of Waterloo)
- Shelly Cohen (UCD)
Modified by Joshua Halpern (Howard University)
Tom Neils (Grand Rapids Community College)