2.4: Phosphines
- Page ID
- 91531
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Tertiary phosphines, PR3 are most notable for their remarkable electronic and steric tunability and their “innocence”—they tend to avoid participating directly in organometallic reactions, but have the ability to profoundly modulate the electronic properties of the metal center to which they’re bound. Furthermore, because the energy barrier to umbrella flipping of phosphines is quite high, “chiral-at-phosphorus” ligands can be isolated in enantioenriched form and introduced to metal centers, bringing asymmetry just about as close to the metal as it can get in chiral complexes. Phosphorus NMR is a technique that Just Works (thanks, nature). Soft phosphines match up very well with the soft low-valent transition metals. Electron-poor phosphines are even good π-acids!
General Properties
Like CO, phosphines are dative, L-type ligands that formally contribute two electrons to the metal center. Unlike CO, most phosphines are not small enough to form more than four bonds to a single metal center (and for large R, the number is even smaller). Steric hindrance becomes a problem when five or more PR3 ligands try to make their way into the space around the metal. An interesting consequence of this fact is that many phosphine-containing complexes do not possess 18 valence electrons. Examples include Pt(PCy3)2, Pd[P(t-Bu)3]2, and [Rh(PPh3)3]+. Doesn’t that just drive you crazy? It drives the complexes crazy as well—and most of these coordinatively unsaturated compounds are wonderful catalysts.
Bridging by phosphines is extremely rare, but ligands containing multiple phosphine donors that bind in an Ln (n > 1) fashion to a single metal center are all over the place. These ligands are called chelating or polydentate to indicate that they latch on to metal centers through multiple binding sites. For entropic reasons, chelating ligands bind to a single metal center at multiple points if possible, instead of attaching to two different metal centers (the aptly named chelate effect). An important characteristic of chelating phosphines is bite angle, defined as the predominant P–M–P angle in known complexes of the ligand. We’ll get into the interesting effects of bite angle later, but for now, we might imagine how “unhappy” a ligand with a preferred bite angle of 120° would be in the square planar geometry. It would much rather prefer to be part of a trigonal bipyramidal complex, for instance.
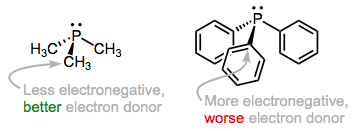
The predominant orbital interaction contributing to phosphine binding is the one we expect, a lone pair on phosphorus interacting with an empty metallic d orbital. The electronic nature of the R groups influences the electron-donating ability of the phosphorus atom. For instance, alkylphosphines, which possess P–Csp3 bonds, tend to be better electron donors than arylphosphines, which possess P–Csp2 bonds. The rationale here is the greater electronegativity of the sp2 hybrid orbital versus the sp3 hybrid, which causes the phosphorus atom to hold more tightly to its lone pair when bound to an sp2 carbon. The same idea applies when electron-withdrawing and -donating groups are incorporated into R: the electron density on P is low when R contains electron-withdrawing groups and high when R contains electron-donating groups. Ligands (and associated metals) in the former class are called electron poor, while those in the latter class are electron rich.
As we add electronegative R groups, the phosphorus atom (and the metal to which it's bound) become more electron poor.
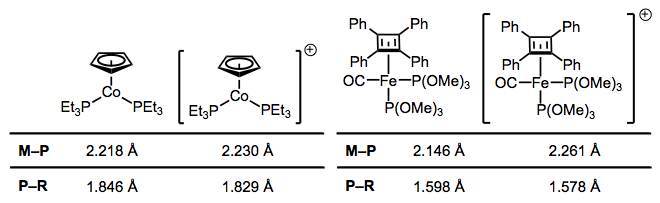
Like CO, phosphines participate in backbonding to a certain degree; however, the phenomenon here is of a fundamentally different nature than CO backbonding. For one thing, phosphines lack a π* orbital. In the days of yore, chemists attributed backbonding in phosphine complexes to an interaction between a metallic dπ orbital and an empty 3d orbital on phosphorus. However, this idea has elegantly been proven bogus, and a much more organicker-friendly explanation has taken its place (no d orbitals on P required!). In an illuminating series of experiments, M–P and P–R bond lengths were measured via crystallography for several redox pairs of complexes. I’ve chosen two illustrative examples, although the linked reference is chock full of other pairs. The question is: how do we explain the changes in bond length upon oxidation?
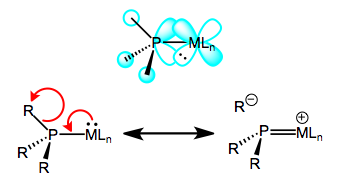
Oxidation decreases the ability of the metal to backbond, because it removes electron density from the metal. This explains the increases in M–P bond length—just imagine a decrease the M–P bond order due to worse backbonding. And the decrease in P–R bond length? It’s important to see that invoking only the phosphorus 3d orbitals would not explain changes in the P–R bond lengths, as the 3d atomic orbitals are most definitely localized on phosphorus. Instead, we must invoke the participation of σ*P–R orbitals in phosphine backbonding to account for the P–R length decreases. When all is said and done, the LUMO of the free phosphine has mostly P–R antibonding character, with some 3d thrown into the mix. The figure below depicts one of the interactions involved in M–P backbonding, a dπ → σ* interaction (an orthogonal dπ → σ* interaction also plays a role). As with CO, a resonance structure depicting an M=P double bond is a useful heuristic! Naturally, R groups that are better able to stabilize negative charge—that is, electron-withdrawing groups—facilitate backbonding in phosphines. Electron-rich metals help too.
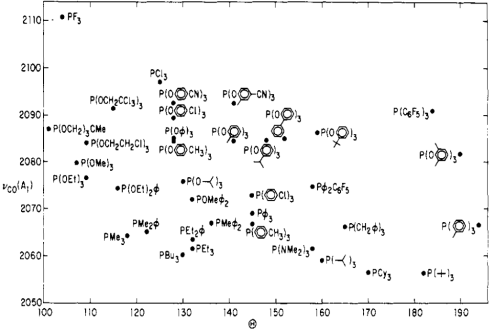
The steric and electronic properties of phosphines vary enormously. Tolman devised some intriguing parameters that characterize the steric and electronic properties of this class of ligands. To address sterics, he developed the idea of cone angle—the apex angle of a cone formed by a point 2.28 Å from the phosphorus atom (an idealized M–P bond length), and the outermost edges of atoms in the R groups, when the R groups are folded back as much as possible. Wider cone angles, Tolman reasoned, indicate greater steric congestion around the phosphorus atom. To address electronics, Tolman used a not-so-old friend of ours—the CO stretching frequency (νCO) of mixed phosphine-carbonyl complexes. Specifically, he used Ni(CO)3L complexes, where L is a tertiary phosphine, as his standard. Can you anticipate Tolman’s logic? How should νCO change as the electron-donating ability of the phosphine ligands increases?
Tolman’s logic went as follows: more strongly electron-donating phosphines are associated with more electron-rich metals, which are better at CO backbonding (due fundamentally to higher orbital energies). Better CO backbonding corresponds to a lower νCO due to decreased C–O bond order. Thus, better donor ligands should be associated with lower νCO values (and vice versa for electron-withdrawing ligands). Was he correct? Exhibit A…
Notice the poor ligand trifluorophosphine stuck in the “very small, very withdrawing” corner, and its utter opposite, the gargantuan tri(tert-butyl)phosphine in the “extremely bulky, very donating” corner. Intriguing! One can learn a great deal just by studying this chart.
Synthesis
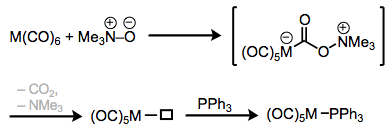
Phosphine complexes are most commonly made through ligand substitution processes—the exchange of one ligand for another on a metal center. One interesting method utilizes tertiary N-oxides to essentially “oxidize off” a CO ligand, leaving behind an open coordination site that may be filled by a phosphine. Notice that the carbon of CO is behaving as an electrophile in this process. Shi and Basolo masterfully demonstrate that an intermediate amine complex cannot be involved in this mechanism. Irradiation by ultraviolet light is an alternative method to coax the CO ligand off of metal carbonyl complexes.
Methods for synthesizing the phosphine ligands themselves are somewhat beyond our scope, but electrophilic phosphorus chemistry is common, particularly when arylphosphines are the target.
Reactions
Phosphines are most often spectator ligands, meaning that they don’t participate in reactions, but hang on for the ride. There are, however, some important exceptions to this rule. First of all, dissociation of a phosphine ligand is often required to generate a site of coordinative unsaturation before catalytic reactions can begin. Good examples are cross-couplings employing the saturated Pd(PPh3)4. This complex is actually just a precatalyst that must lose phosphine ligands to enter the catalytic cycle of cross-coupling. Phosphine association is also an important step of many catalytic reactions.
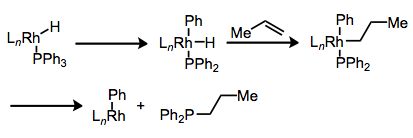
What decomposition pathways are available to phosphine ligands? P–C bond cleavage is a surprisingly common process. In general, the idea is that the metal center can insert into the P–C bond via concerted oxidative addition, then reductively eliminate to establish a new P–C bond. Reductive elimination can even occur after some intermediate steps, as in the example below.
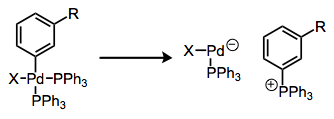
Phosphonium salt formation from arylphosphine complexes is a related process. Here, the complex essentially just falls apart after P–C reductive elimination.
Phosphine ligands are everywhere, and we’ll definitely see more of this fascinating class of ligands in the future. They are particularly powerful as the bearers of asymmetry in chiral metal complexes, which are used to prepare enantioenriched organic products.