2.2: Predicting the Geometry of Organometallic Complexes
- Page ID
- 91782
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)An important issue that we’ve glossed over until now concerns what organometallic complexes actually look like: what are their typical geometries? Can we use any of the “bookkeeping metrics” we’ve explored so far to reliably predict geometry? The answer to the latter questions is a refreshing but qualified “yes.” In this post, we’ll explore the possibilities for complex geometry and develop some general guidelines for predicting geometry. In the process we’ll enlist the aid of a powerful theoretical ally, crystal field theory (CFT), which provides some intuitive explanations for geometry the geometry of organometallic complexes.
Introduction
Because OM complexes feature a variety of coordination numbers, the possibilities for geometry are numerous. The common geometries of organic chemistry—linear, pyramidal, trigonal planar, and tetrahedral—are available to organometallic complexes too. Many complexes exhibit a second kind of four-coordinate geometry, square planar. Five-coordinate complexes may exhibit either square pyramidal or trigonal bipyramidal geometries. Six-coordinate complexes feature either octahedral geometry or the rare but intriguing trigonal prismatic arrangement. The figure below summarizes these possibilities (minus the two-coordinate geometries, which we will not deal with).
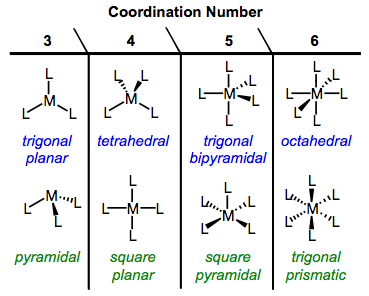
Common geometries of organometallic complexes.
Geometries whose names are colored blue are favored for steric reasons (that is, ligands are as far apart as possible). Geometries colored green may be favored for electronic reasons, and our next task is to understand the meaning behind the cryptic phrase “electronic reasons.” Important questions to keep in mind: what is meant by the term “electronic factors”? When are electronic factors important? And most fundamentally, how do we imagine ligands perturbing the energies of electrons on a metal center?
Let’s return to the primordial analogy of negatively charged, electron-rich ligands flying through space toward an atomic metal cation to form an organometallic complex. Let’s begin with a prescribed geometry…say, square planar. The fundamental tenet of crystal field theory is that, as the negatively charged ligands approach the metal, they will influence the energy of the metallic d orbitals with which they overlap. More specifically, filled ligand orbitals will raise the energy of orbitals with which they most directly overlap. This makes intuitive sense—like charges repel, and d orbitals (which contain negative electrons) should increase in energy when exposed to negatively charged (and/or electron-rich) filled ligand orbitals. Now, let’s imagine the ligands approaching in the xy-plane, along the positive and negative x- and y-axes, to form the square planar geometry. This approach is shown in the figure below, overlaid on images of the d orbitals. White arrows (some of which are omitted to indicate occlusion by the orbital) illustrate the “attack vectors” of the ligands.
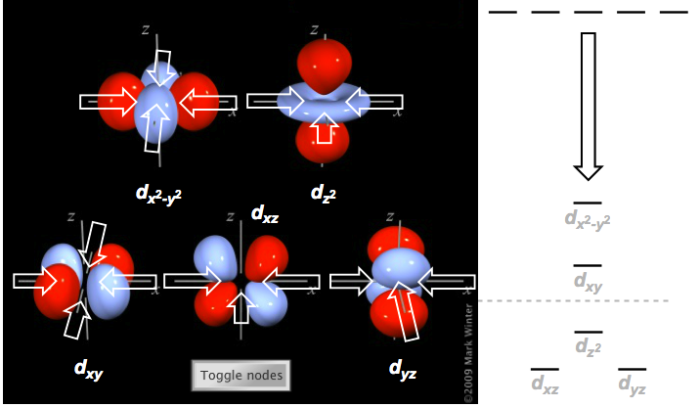
Ligands approaching a metal center along the "attack vectors" of the square planar geometry. How can we justify the indicated orbital energy changes?
The right half of the diagram shows how the distribution of d orbital energies changes as the ligands approach. Notice that the dx2–y2 orbital, whose lobes directly oppose the attack vectors, becomes the highest-energy orbital! This isn’t surprising in light of the ideas of crystal field theory described above. The dxy orbital faces a similar fate, although the overlap is not quite as direct, so its increase in energy is not as severe. Even the dz2 orbital seems to exhibit some overlap via its “donut” lobe. The orbitals completely perpendicular to the xy-plane, the dxz and dyz orbitals, exhibit no overlap with the approaching filled ligand orbitals, and in fact are strongly stabilized by the approaching ligands. A similar analysis can be carried out for the other possible geometries; see this link for the results. I encourage you to try some of the others on your own! The octahedral case is particularly instructive—which two d orbitals would you expect to be strongly destabilized by approaching octahedral ligands?
Crystal field theory’s perturbed d orbital sets can be used, in combination with the number of d electrons on the metal center, to predict geometry with a fair degree of accuracy. The key question we need to address is: which arrangement of d orbital energies (that is, which geometry) keeps the d electrons as stable as possible?
Example \(\PageIndex{1}\):
Let’s explore an example. d8, Pd(II) complexes like (PPh3)2Pd(Ph)Br are ubiquitous in palladium-catalyzed cross-coupling reactions. Two geometries are possible here, and I’ve provided the perturbed d orbital “scaffolds” for each arrangement. Which orbital set holds the 8 d electrons in the more stable way?
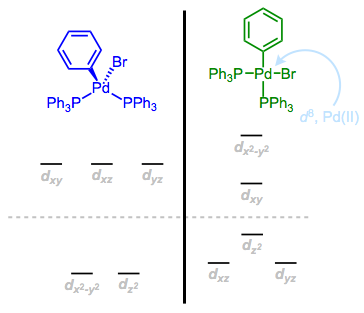
Try mentally filling each orbital set with 8 electrons. Which geometry provides the most stability?
We can see that the tetrahedral orbital set would cause significant problems for 8 electrons, as four would end up in the antibonding levels, and two would be unpaired. The square planar orbitals make the best of a bad situation and accommodate one antibonding lone pair, which is well compensated for by the six bonding electrons. Additionally, the energy of the highest occupied orbital is lower overall for the square planar complex. Thus, we should expect the Pd(II) complex to be square planar. Crystallographic studies support this prediction.
The above analysis hinged on an understanding of how approaching ligands influence d orbital energies, and there are a couple of other considerations we need to address to fully flesh out these ideas. First of all, the nature of the ligands influences how extreme the energy perturbations are. More electron-donating ligands, generally, cause more significant energy perturbations. The spectrochemical series can be used to predict the extent of splitting caused by approaching ligands. We’ll leave it at that, but it’s worth keeping in mind that “electronic factors” are more important for some ligands than others. Secondly, the metal’s size influences the relative importance of steric and electronic factors. For d8 nickel(II) complexes, steric factors can be quite important and tetrahedral geometry is often observed. However, tack strongly electron-donating ligands like –CH3 on to the nickel(II) center, and all of a sudden, square planar geometry is favored because electronic factors dominate. In cases like this, it can be difficult to predict which factor, sterics or electronics, will dictate geometry.

