7.1: Reading

7.1. Drug discovery & development process

The drug discovery and development process is very resource-intensive and time-consuming. Bringing a new drug to market (from drug discovery through clinical trials to marketing approval) typically takes between 10 and 15 years and costs $1.395 billion (2013 dollars) on average [1]. Figure 1 shows a schematic diagram of the drug discovery and development process.

Copy and Paste Caption here

Figure 1. Drug discovery and development process.

The process presented in Figure 1 is simplified, ignoring many details within each stage. In reality, the drug discovery and development process is much more complicated, as illustrated in this Figure (https://www.nature.com/articles/nrd.2017.217/figures/1) [2].

This chapter describes some computational approaches used in the drug discovery stage. To further discuss computer-aided (or computer-assisted) drug discovery, it is necessary to learn the following commonly used terms.

• Actives
  Substances that meet a threshold level of activity in a primary screen, which typically measures the activity of compounds against the target at a single concentration. Because the activity was measured only at a single concentration, it is not possible to tell whether a compound can interact with the target in a dose-response way. Often the structure and purity of screening substances are not confirmed.
  • Hits
    Hits are compounds with intrinsic activity (IC50, EC50, etc.) against the target and they are characterized through secondary assays (which measure compounds’ activity at multiple concentrations). In general, because hits have limited potency and/or selectivity, they are not suitable for in vivo studies (in animals or humans). However, they provide a starting point for structure activity relationship (SAR) analysis to help improve potency/selectivity and other drug properties.
    
• Leads
  A Lead represents a compound series that shows a relationship between chemical structure and target-based activity (in biochemical and cell-based assays). Compounds within the series have physicochemical properties, potency and selectivity deemed appropriate for in vivo evaluation.
  
• Drug candidates
  Compounds with strong therapeutic potential and whose activity and specificity have been optimized through the lead optimization step. These compounds move to the preclinical development stage for in vivo animal testing.

Copy and Paste Caption here

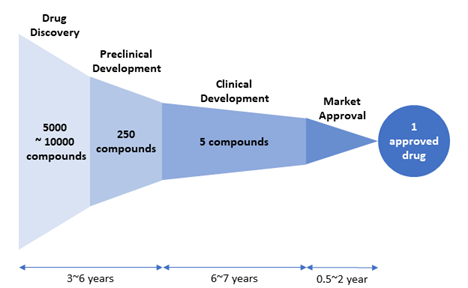
Figure 2. Drug attrition rate. Of 5,000–10,000 compounds experimentally screened in the drug discovery stage, approximately 250 will enter preclinical testing and 5 will enter clinical testing. Only one compound of them will be approved. [Adapted from “New Drug Approvals in 2011” (http://phrma-docs.phrma.org/sites/default/files/pdf/nda2011.pdf)].

7.2. What is virtual screening?

Virtual screening (VS) is a computational technique used in drug discovery to prioritize the compound selection from a large compound library for subsequent experimental assays. VS aims to ensure that those molecules with the largest a priori probabilities of being active against the target (protein/gene/disease) are tested first in a lead discovery program. VS is a cost-effective approach that complements high-throughput screening and it is routinely used in drug discovery projects.

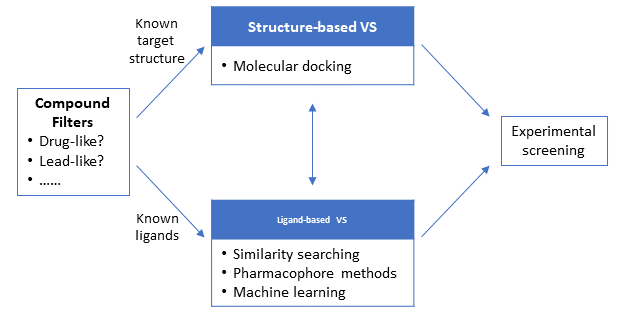
Depending on the information available about the target and/or its ligands at the beginning of the VS campaign, VS can be broadly divided into two main approaches: structure-based and ligand-based approaches. The structure-based approaches, such as molecular docking, use the 3-D structure of the target macromolecule (protein/gene) to dock the candidate molecules and rank them based on their predicted binding affinity or complementarity to the binding site. On the other hand, the ligand-based approaches use a set of known actives against the target to identify database compounds that are likely to be active based on similarity/commonality between the known actives and database compounds. Because the structure-based approaches require the 3-D structural information of the target macromolecules, they are not a feasible option when the 3-D structure of the target is not available. In contrast, the ligand-based approaches can be used regardless of whether the target 3-D structure is available or not.

Figure 3. A schematic diagram of the virtual screening process, which involves many computational approaches to prioritize the compound selection for further experiments

.

7.3. Compound Filters

When screening a large compound library for drug discovery, it is desirable to identify problematic compounds that are not likely to lead to successful drug discovery campaign and exclude them from further computational or experimental screening. For example, if a molecule is not absorbed very well by the human body, that molecule may not be a good candidate for an orally administered drug, even if it shows a good activity against the target protein in in vitro testing. Therefore, one may want to exclude this compound from further testing.

Lipinski's rule of five (also known as the Pfizer's rule of five) (RO5) [3] is a rule of thumb to evaluate “drug-likeness” and helps determine whether a compound has good solubility and permeability that would make the compound a likely orally administered drug in human. According to RO5, drug-like compounds have:

• No more than 5 hydrogen-bond donors
• No more than 10 hydrogen-bond acceptors
• Molecular weight of 500 or less
• Calculated logP (CLogP) less than 5

Lipinski and coworkers [3] analyzed 2245 compounds that had reached phase II trials or higher and formulated RO5 based on the observation that most orally administered drugs are relatively small and moderately lipophilic.

While RO5 provides a fast and simple way to estimate oral bioavailability of molecules, it is a rule of thumb, not accurate and hard-set criteria. For example, ~16% of orally administrated drugs violate at least one criterion of RO5 [4]. For this reason, several variants of RO5 have been proposed as explained in detail in a recent review article [5].

An interesting concept related to drug-likeness is “lead-likeness”[6-9]. In the analysis of 470 lead-drug pairs, Hann et al [6]. found that, on average, lead compounds had lower molecular weight and logP and fewer hydrogen bond acceptors and more hydrogen bond donors, compared to the respective drugs developed from them. Therefore, it can be problematic to apply drug-likeness filters to compound libraries designed for lead discovery. This led to the development of “lead-likeness” filters. An example is Congreve’s rule of 3 (RO3) for lead-like compounds [10], which include:

• The number of hydrogen bond donors ≤3
• The number of hydrogen bond acceptors ≤ 3
• Molecular weight < 300
• ClogP ≤ 3

In general, the lead optimization step in drug discovery involves the modification of the lead molecule to give the final drug and this typically increases the molecular “complexity”, as reflected in the differences between RO3 and RO5. For this reason, some people argue that lead-like filters, rather than drug-like filters, should be used when performing virtual screening [6,7]. More detailed discussion about drug-likeness and lead-likeness can be found elsewhere [6-9].

7.4. Structure-based virtual screening

Structural-based approaches, exemplified by molecular docking, require the 3-D structure of the target macromolecule, which can be either experimentally determined through X-ray crystallography or computationally predicted through homology modeling. In molecular docking, the most likely binding mode for each compound is identified and assign a priority order to the molecules. While a large number of molecular docking methods have been proposed, all of them have two essential components to solve the molecular docking problem:

· docking algorithm, used to possible protein-ligand geometries (also called “poses”), and

· scoring function, which is a mathematical formula used to score or rank these poses.

Docking algorithms

Molecular docking methods can be classified into rigid-body docking and flexible docking, depending on the degree to which the flexibility of ligands and their macromolecule target is considered during the docking process. The rigid-body docking uses “fixed” structures of the ligands and target, treating them as rigid bodies. While the earliest docking programs used the rigid-body docking approach, more recent programs can explore the conformational space of the ligands (by changing the torsional angles of the ligands during the docking process). Some programs also permit conformational flexibility to the protein. Because rigid-body docking is faster than flexible docking, rigid docking may be preferred for initial quick screening a very large compound library. However, poses from such initial rigid docking need to be refined and optimized through flexible docking methods. In addition, because of the advance of computational resources and efficiency, flexible docking is becoming more popular. There are several approaches to take ligand flexibility in molecular docking, including:

· Systematic methods: incorporate ligand flexibility by gradually changing structural parameters of the ligands (such as torsional angles, translational and rotational degrees of freedom). Because large conformational space prohibits an exhaustive systematic search, some algorithms use heuristics to focus on regions on conformational space that are likely to contain good poses. While effective in conformational search, it can find a local minimum, rather than the global minimum.

· Stochastic methods: makes random changes to the ligand structure to perform the conformational search. It generates an ensemble of conformations that populates a wide range of the energy landscape. While this avoids trapping the final structure at a local energy minimum and increases the probability of finding the global minimum. However, it covers a broader range of the energy landscape, it is computationally more expensive.

· Genetic algorithms [11,12]: use the concepts of evolution and natural selection. It begins with encoding structural parameters of the initial structure in a vector (called a chromosome) and generating an ensemble (or population) of chromosomes using the random search algorithm. Each chromosome in this population is evaluated and the most “adapted” ones (with the lowest energy values) are selected as “templates” for the generation of next population. Each iteration of this process will lead to lower-energy binding poses than those from the previous iteration and after a reasonable number of iterations, the chromosome population will converge to a chromosome corresponding to the global energy minimum.

Scoring Functions

Scoring functions [13] are used to evaluate the binding affinity between the ligand and its target. different scoring functions have been developed over the years, and they can be broadly classified into four groups: (1) force-field-based, (2) empirical scoring functions, (3) knowledge-based functions, and (4) consensus-scoring functions.

· Force-field scoring functions
Force-field scoring functions use force field parameters used in molecular mechanics calculations. These parameters are derived from experimental data and ab initio quantum mechanical calculations. The force field scorning functions estimate the binding energy by summing the contributions of various bonded terms (e.g., stretching, bending, and torsional forces) and non-bonded terms (e.g., electrostatic and van der Waals interactions). An example of this type of scoring functions is the one used by DOCK [14], whose energy parameters are taken from the AMBER force fields [15,16].

· Empirical scoring functions
Empirical scoring functions [17-19] express the binding energy of a protein-ligand complex as a weighted sum of terms that represent physical events involved in the complex formation, such hydrogen bonding, hydrophobic contact, desolvation effects (due to the loss of solvent (water) molecules that stabilizes the ligand), and entropy penalty (due to the loss of ligand flexibility upon the complex formation). The weight and parameters in each term are empirically determined through regression analysis of a set of protein-ligand complexes with known binding affinities. While the performance of empirical scoring functions relies on the accuracy of the experimental data used to develop them, they are faster than force-field-based scoring functions. Empirical scoring functions are used in some popular molecular docking programs like Surflex [20] and FlexX [21,22].

· Knowledge-based functions
Knowledge-based functions [23-27] exploit information contained in experimentally determined 3-D structures of protein-ligand complexes. For each ligand-protein atom pair, an interaction potential is generated, which gives the pairwise interaction energy as a function of their separation. These potentials are generated through statistical analysis of the interatomic distance distribution observed in known protein-ligand complexes. The underlying assumption in this approach is that interatomic contacts observed more often in the data set are likely to represent favorable contacts that increase the binding affinity, while those contacts occurring with less frequency are unfavorable and likely to decrease the binding affinity. The final score is computed from these individual interactions.

· Consensus scoring functions
Because each scoring function has its strength and weakness, consensus scoring [28-33] has been gaining popularity more recently, which simultaneously uses multiple scoring approaches together to achieve improved accuracies. Many consensus-scoring strategies have been proposed and examples are MultiScore [29], X-CSCORE [30], GFscore [31], supervised consensus scoring (SCS) [32], and SeleX-CS [33].

7.5. Ligand-based virtual screening

Ligand-based approaches use a set of active compounds that are known to interact with the target protein. These approaches are based on the Similar Property Principle, which states structurally similar molecules are likely to have similar (physicochemical and biological) properties. In contrast to structure-based approaches, the ligand-based approaches can be applied when the structure of the target macromolecule is not known. Examples of ligand-based approaches are:

· Pharmacophore methods: identify the pharmacophore pattern common to a set of known actives and uses this pattern in a subsequent substructure search. IUPAC defines a pharmacophore as “the ensemble of steric and electronic features that is necessary to ensure the optimal supramolecular interactions with a specific biological target structure and to trigger (or to block) its biological response.”[34]

· Machine learning methods: use prediction models developed from a training set containing known actives and known inactives. These methods will be discussed in Chapter 8.

· Similarity methods: find molecules structurally similar to known active molecules, based on similarity measures. This topic was discussed in Chapter 6.

7.6. Prediction of ADMET Properties

During the drug discovery and development process, it is very important to consider not only how tightly a potential drug molecule can bind to the target protein (pharmacodynamics), but also how the molecule reach its site of action within the body (pharmacokinetics). This involves the absorption of the drug molecule by the body and the drug transport to the target organ/tissue. While a sufficient number of drug molecules should be available in the body to give the desired therapeutic effect but they must ultimately be removed from the body through metabolism and excretion. In addition, neither the drug nor its metabolites should be toxic. In pharmacology, these properties are often referred to as ADMET properties (which stands for Absorption, Distribution, Metabolism, Excretion, and Toxicity).

During the drug discovery process, various computational tools are routinely used to predict a wide range of ADMET properties of compounds [35-38], including:

· Solubility in water, which affects oral bioavailability of the drug.

· Caco-2 cell monolayer permeability, which is an experimental model for evaluating the intestinal absorption of drugs.

· Permeability through blood-brain barrier between the systemic circulation and the brain.

· Interaction with cytochrome P450 (CYP) proteins involved in drug metabolism.

· Binding affinity to Human ether-a-go-go related gene (hERG) protein, which is responsible for cardiotoxicity of many drugs.

· Interaction with P-glycoprotein efflux pump, involved in the active transport of various compounds out of cells [39].

· Plasma-protein binding, which help estimates the amount of free drugs that can cross membranes.

7.7. Further Reading

· Principles of early drug discovery

https://doi.org/10.1111/j.1476-5381.2010.01127.x

https://www.ncbi.nlm.nih.gov/pmc/articles/PMC3058157/

· Recognizing Pitfalls in Virtual Screening: A Critical Review
https://doi.org/10.1021/ci200528d

· ADMET IN SILICO MODELLING: TOWARDS PREDICTION PARADISE?
https://doi.org/10.1038/nrd1032

· Computational Methods in Drug Discovery

https://doi.org/10.1124/pr.112.007336

https://www.ncbi.nlm.nih.gov/pmc/articles/PMC3880464/

· Scoring functions and their evaluation methods for protein–ligand docking: recent advances and future directions

https://doi.org/10.1039/C0CP00151A

· Empirical Scoring Functions for Structure-Based Virtual Screening: Applications, Critical Aspects, and Challenges
https://doi.org/10.3389/fphar.2018.01089

https://www.ncbi.nlm.nih.gov/pmc/articles/PMC6165880/

References

1. DiMasi JA, Grabowski HG, Hansen RW: Innovation in the pharmaceutical industry: New estimates of R&D costs. J Health Econ 2016, 47:20-33.

2. Wagner J, Dahlem AM, Hudson LD, Terry SF, Altman RB, Gilliland CT, DeFeo C, Austin CP: A dynamic map for learning, communicating, navigating and improving therapeutic development. Nat Rev Drug Discov 2018, 17:151-153.

3. Lipinski CA, Lombardo F, Dominy BW, Feeney PJ: Experimental and computational approaches to estimate solubility and permeability in drug discovery and development settings. Adv Drug Deliv Rev 1997, 23:3-25.

4. Bickerton GR, Paolini GV, Besnard J, Muresan S, Hopkins AL: Quantifying the chemical beauty of drugs. Nat Chem 2012, 4:90-98.

5. Mignani S, Rodrigues J, Tomas H, Jalal R, Singh PP, Majoral JP, Vishwakarma RA: Present drug-likeness filters in medicinal chemistry during the hit and lead optimization process: how far can they be simplified? Drug Discov Today 2018, 23:605-615.

6. Hann MM, Leach AR, Harper G: Molecular complexity and its impact on the probability of finding leads for drug discovery. J Chem Inf Comput Sci 2001, 41:856-864.

7. Teague SJ, Davis AM, Leeson PD, Oprea T: The design of leadlike combinatorial libraries. Angew Chem-Int Edit 1999, 38:3743-3748.

8. Oprea TI, Davis AM, Teague SJ, Leeson PD: Is there a difference between leads and drugs? A historical perspective. J Chem Inf Comput Sci 2001, 41:1308-1315.

9. Oprea TI, Allu TK, Fara DC, Rad RF, Ostopovici L, Bologa CG: Lead-like, drug-like or "pub-like": how different are they? J Comput-Aided Mol Des 2007, 21:113-119.

10. Congreve M, Carr R, Murray C, Jhoti H: A rule of three for fragment-based lead discovery? Drug Discov Today 2003, 8:876-877.

11. Morris GM, Goodsell DS, Halliday RS, Huey R, Hart WE, Belew RK, Olson AJ: Automated docking using a Lamarckian genetic algorithm and an empirical binding free energy function. J Comput Chem 1998, 19:1639-1662.

12. Jones G, Willett P, Glen RC, Leach AR, Taylor R: Development and validation of a genetic algorithm for flexible docking. J Mol Biol 1997, 267:727-748.

13. Huang SY, Grinter SZ, Zou XQ: Scoring functions and their evaluation methods for protein-ligand docking: recent advances and future directions. Phys Chem Chem Phys 2010, 12:12899-12908.

14. Meng EC, Shoichet BK, Kuntz ID: AUTOMATED DOCKING WITH GRID-BASED ENERGY EVALUATION. J Comput Chem 1992, 13:505-524.

15. Weiner SJ, Kollman PA, Case DA, Singh UC, Ghio C, Alagona G, Profeta S, Weiner P: A NEW FORCE-FIELD FOR MOLECULAR MECHANICAL SIMULATION OF NUCLEIC-ACIDS AND PROTEINS. J Am Chem Soc 1984, 106:765-784.

16. Weiner SJ, Kollman PA, Nguyen DT, Case DA: AN ALL ATOM FORCE-FIELD FOR SIMULATIONS OF PROTEINS AND NUCLEIC-ACIDS. J Comput Chem 1986, 7:230-252.

17. Murray CW, Auton TR, Eldridge MD: Empirical scoring functions. II. The testing of an empirical scoring function for the prediction of ligand-receptor binding affinities and the use of Bayesian regression to improve the quality of the model. J Comput-Aided Mol Des 1998, 12:503-519.

18. Guedes IA, Pereira FSS, Dardenne LE: Empirical Scoring Functions for Structure-Based Virtual Screening: Applications, Critical Aspects, and Challenges. Front Pharmacol 2018, 9:18.

19. Eldridge MD, Murray CW, Auton TR, Paolini GV, Mee RP: Empirical scoring functions .1. The development of a fast empirical scoring function to estimate the binding affinity of ligands in receptor complexes. J Comput-Aided Mol Des 1997, 11:425-445.

20. Jain AN: Surflex: Fully automatic flexible molecular docking using a molecular similarity-based search engine. J Med Chem 2003, 46:499-511.

21. Kramer B, Rarey M, Lengauer T: Evaluation of the FLEXX incremental construction algorithm for protein-ligand docking. Proteins 1999, 37:228-241.

22. Rarey M, Kramer B, Lengauer T, Klebe G: A fast flexible docking method using an incremental construction algorithm. J Mol Biol 1996, 261:470-489.

23. Muegge I, Martin YC: A general and fast scoring function for protein-ligand interactions: A simplified potential approach. J Med Chem 1999, 42:791-804.

24. Mitchell JBO, Laskowski RA, Alex A, Thornton JM: BLEEP - Potential of mean force describing protein-ligand interactions: I. Generating potential. J Comput Chem 1999, 20:1165-1176.

25. Mitchell JBO, Laskowski RA, Alex A, Forster MJ, Thornton JM: BLEEP - Potential of mean force describing protein-ligand interactions: II. Calculation of binding energies and comparison with experimental data. J Comput Chem 1999, 20:1177-1185.

26. Huang SY, Zou XQ: An iterative knowledge-based scoring function to predict protein-ligand interactions: I. Derivation of interaction potentials. J Comput Chem 2006, 27:1866-1875.

27. Huang SY, Zou XQ: An iterative knowledge-based scoring function to predict protein-ligand interactions: II. Validation of the scoring function. J Comput Chem 2006, 27:1876-1882.

28. O'Boyle NM, Liebeschuetz JW, Cole JC: Testing Assumptions and Hypotheses for Rescoring Success in Protein-Ligand Docking. J Chem Inf Model 2009, 49:1871-1878.

29. Terp GE, Johansen BN, Christensen IT, Jorgensen FS: A new concept for multidimensional selection of ligand conformations (MultiSelect) and multidimensional scoring (MultiScore) of protein-ligand binding affinities. J Med Chem 2001, 44:2333-2343.

30. Wang RX, Lai LH, Wang SM: Further development and validation of empirical scoring functions for structure-based binding affinity prediction. J Comput-Aided Mol Des 2002, 16:11-26.

31. Betzi S, Suhre K, Chetrit B, Guerlesquin F, Morelli X: GFscore: A general nonlinear consensus scoring function for high-throughput docking. J Chem Inf Model 2006, 46:1704-1712.

32. Teramoto R, Fukunishi H: Supervised consensus scoring for docking and virtual screening. J Chem Inf Model 2007, 47:526-534.

33. Bar-Haim S, Aharon A, Ben-Moshe T, Marantz Y, Senderowitz H: SeleX-CS: A New Consensus Scoring Algorithm for Hit Discovery and Lead Optimization. J Chem Inf Model 2009, 49:623-633.

34. Wermuth G, Ganellin CR, Lindberg P, Mitscher LA: Glossary of terms used in medicinal chemistry (IUPAC Recommendations 1998). Pure Appl Chem 1998, 70:1129-1143.

35. Norinder U, Bergstrom CAS: Prediction of ADMET properties. ChemMedChem 2006, 1:920-937.

36. Moroy G, Martiny VY, Vayer P, Villoutreix BO, Miteva MA: Toward in silico structure-based ADMET prediction in drug discovery. Drug Discov Today 2012, 17:44-55.

37. Gleeson MP: Generation of a set of simple, interpretable ADMET rules of thumb. J Med Chem 2008, 51:817-834.

38. van de Waterbeemd H, Gifford E: ADMET in silico modelling: Towards prediction paradise? Nat Rev Drug Discov 2003, 2:192-204.

39. Li D, Chen L, Li YY, Tian S, Sun HY, Hou TJ: ADMET Evaluation in Drug Discovery. 13. Development of in Silico Prediction Models for P-Glycoprotein Substrates. Mol Pharm 2014, 11:716-726.

Contact Bob Belford, [e-mail] if you have any questions.