6.3: Quantifying Heat and Work
- Last updated
- Save as PDF
- Page ID
- 174937
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Learning Objectives
- To calculate changes in internal energy
- Distinguish the related properties of heat, thermal energy, and temperature
- Define and distinguish specific heat and heat capacity, and describe the physical implications of both
- Perform calculations involving heat, specific heat, and temperature change
Thermal energy is kinetic energy associated with the random motion of atoms and molecules. Temperature is a quantitative measure of “hot” or “cold.” When the atoms and molecules in an object are moving or vibrating quickly, they have a higher average kinetic energy (KE), and we say that the object is “hot.” When the atoms and molecules are moving slowly, they have lower KE, and we say that the object is “cold” (Figure \(\PageIndex{1}\)). Assuming that no chemical reaction or phase change (such as melting or vaporizing) occurs, increasing the amount of thermal energy in a sample of matter will cause its temperature to increase. And, assuming that no chemical reaction or phase change (such as condensation or freezing) occurs, decreasing the amount of thermal energy in a sample of matter will cause its temperature to decrease.
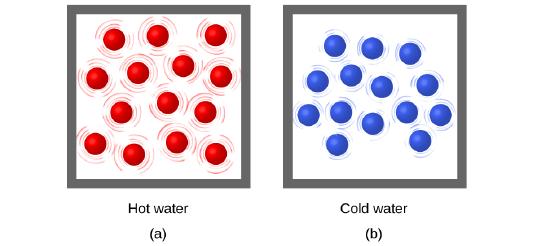
Figure \(\PageIndex{1}\): (a) The molecules in a sample of hot water move more rapidly than (b) those in a sample of cold water.
Heat (q) is the transfer of thermal energy between two bodies at different temperatures. Heat flow (a redundant term, but one commonly used) increases the thermal energy of one body and decreases the thermal energy of the other. Suppose we initially have a high temperature (and high thermal energy) substance (H) and a low temperature (and low thermal energy) substance (L). The atoms and molecules in H have a higher average KE than those in L. If we place substance H in contact with substance L, the thermal energy will flow spontaneously from substance H to substance L. The temperature of substance H will decrease, as will the average KE of its molecules; the temperature of substance L will increase, along with the average KE of its molecules. Heat flow will continue until the two substances are at the same temperature (Figure \(\PageIndex{2}\)).
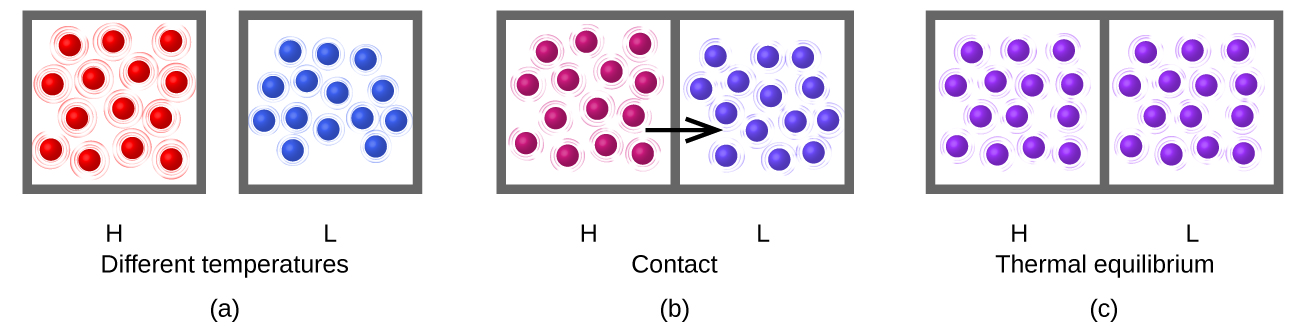
Figure \(\PageIndex{2}\): (a) Substances H and L are initially at different temperatures, and their atoms have different average kinetic energies. (b) When they are put into contact with each other, collisions between the molecules result in the transfer of kinetic (thermal) energy from the hotter to the cooler matter. (c) The two objects reach “thermal equilibrium” when both substances are at the same temperature, and their molecules have the same average kinetic energy.
Matter undergoing chemical reactions and physical changes can release or absorb heat. A change that releases heat is called an exothermic process. For example, the combustion reaction that occurs when using an oxyacetylene torch is an exothermic process—this process also releases energy in the form of light as evidenced by the torch’s flame (Figure \(\PageIndex{3a}\)). A reaction or change that absorbs heat is an endothermic process. A cold pack used to treat muscle strains provides an example of an endothermic process. When the substances in the cold pack (water and a salt like ammonium nitrate) are brought together, the resulting process absorbs heat, leading to the sensation of cold.

Figure \(\PageIndex{3}\): (a) An oxyacetylene torch produces heat by the combustion of acetylene in oxygen. The energy released by this exothermic reaction heats and then melts the metal being cut. The sparks are tiny bits of the molten metal flying away. (b) A cold pack uses an endothermic process to create the sensation of cold. (credit a: modification of work by “Skatebiker”/Wikimedia commons).
Historically, energy was measured in units of calories (cal). A calorie is the amount of energy required to raise one gram of water by 1 degree C (1 kelvin). However, this quantity depends on the atmospheric pressure and the starting temperature of the water. The ease of measurement of energy changes in calories has meant that the calorie is still frequently used. The Calorie (with a capital C), or large calorie, commonly used in quantifying food energy content, is a kilocalorie. The SI unit of heat, work, and energy is the joule. A joule (J) is defined as the amount of energy used when a force of 1 newton moves an object 1 meter. It is named in honor of the English physicist James Prescott Joule. One joule is equivalent to 1 kg m2/s2, which is also called 1 newton–meter. A kilojoule (kJ) is 1000 joules. To standardize its definition, 1 calorie has been set to equal 4.184 joules.
\[1\,cal \equiv 4.184\, J\]
Application: Heat can do more than increase temperature
Most substances expand as their temperature increases and contract as their temperature decreases. This property can be used to measure temperature changes, as shown in Figure \(\PageIndex{4}\). The operation of many thermometers depends on the expansion and contraction of substances in response to temperature changes.

Direction of Heat Flow: Endothermic vs. Exothermic Processes
The reaction of powdered aluminum with iron(III) oxide, known as the thermite reaction, generates an enormous amount of heat—enough, in fact, to melt steel. The balanced chemical equation for the reaction is as follows:
\[ \ce{2Al(s) + Fe_2O_3(s) \rightarrow 2Fe(s) + Al_2O_3(s) }\label{12.2.1}\]
We can also write this chemical equation as
\[\ce{2Al(s) + Fe_2O_3(s) \rightarrow 2Fe(s) + Al_2O_3(s)} + \text{heat} \label{12.2.2}\]
to indicate that heat is one of the products. Chemical equations in which heat is shown as either a reactant or a product are called thermochemical equations. In this reaction, the system consists of aluminum, iron, and oxygen atoms; everything else, including the container, makes up the surroundings. During the reaction, so much heat is produced that the iron liquefies. Eventually, the system cools; the iron solidifies as heat is transferred to the surroundings. A process in which heat (\(q\)) is transferred from a system to its surroundings is described as exothermic. By convention, \(q < 0\) for an exothermic reaction.
When you hold an ice cube in your hand, heat from the surroundings (including your hand) is transferred to the system (the ice), causing the ice to melt and your hand to become cold. We can describe this process by the following thermochemical equation:
\[ \text{heat} + \ce{H_2O_{(s)} \rightarrow H_2O_{(l)}} \label{12.2.3}\]
When heat is transferred to a system from its surroundings, the process is endothermic. By convention, \(q > 0\) for an endothermic reaction.
By convention, \(q < 0\) for an exothermic reaction and \(q > 0\) for an endothermic reaction.
Exercise \(\PageIndex{1}\)
Decide whether the following are endothermic or exothermic processes
- water evaporates off a shower door
- an acid tablet being added to a pool and the surrounding water heats up
- \(\ce{NH_4Cl}\) is dissolved in water and the solution cools
- the burning of a log in a campfire
- Hint
-
During an endothermic process heat is absorbed from surroundings, causing them to cool, so in every case where there is cooling there is most likely an endothermic process taking place. For exothermic reactions energy is being released to the surroundings and so the surroundings feel like they have been heated by the process.
- Answer a
-
endothermic
- Answer b
-
exothermic
- Answer c
-
endothermic
- Answer d
-
exothermic
Heat is technically not a component in Chemical Reactions
Technically, it is poor form to have a \(heat\) term in the chemical reaction like in Equations \(\ref{12.2.2}\) and \(\ref{12.2.3}\) since is it not a true species in the reaction. However, this is a convenient approach to represent exothermic and endothermic behavior and is commonly used by chemists.
Contributors and Attributions
Paul Flowers (University of North Carolina - Pembroke), Klaus Theopold (University of Delaware) and Richard Langley (Stephen F. Austin State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at http://cnx.org/contents/85abf193-2bd...a7ac8df6@9.110).
Learning Objectives
- To know the relationship between energy, work, and heat.
One definition of energy is the capacity to do work. There are many kinds of work, including mechanical work, electrical work, and work against a gravitational or a magnetic field. Here we will consider only mechanical work and focus on the work done during changes in the pressure or the volume of a gas.
Mechanical Work
The easiest form of work to visualize is mechanical work (Figure \(\PageIndex{5}\)), which is the energy required to move an object a distance \(d\) when opposed by a force \(F\), such as gravity:
\[w=F\,d \label{12.3.1}\]
with \(w\) is work, \(F\) is opposing force, and \(d\) is distance.
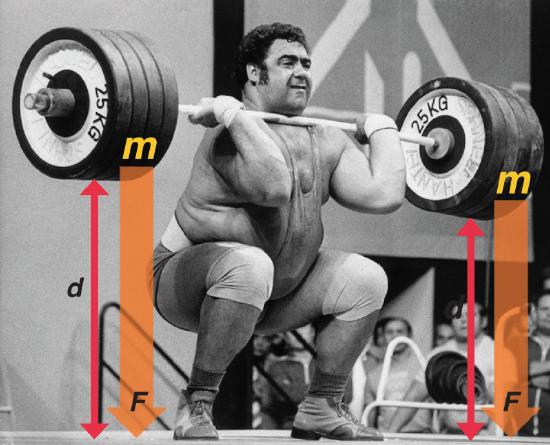
Because the force (\(F\)) that opposes the action is equal to the mass (\(m\)) of the object times its acceleration (\(a\)), Equation \(\ref{12.3.1}\) can be rewritten to:
\[w = m\,a\,d \label{12.3.2}\]
with \(w\) is work, \(m\) is mass, \(a\) is acceleration, and \(d\) is distance.
Recall from that weight is a force caused by the gravitational attraction between two masses, such as you and Earth. Hence for works against gravity (on Earth), \(a\) can be set to \(g=9.8\; m/s^2)\). Consider the mechanical work required for you to travel from the first floor of a building to the second. Whether you take an elevator or an escalator, trudge upstairs, or leap up the stairs two at a time, energy is expended to overcome the opposing force of gravity. The amount of work done (w) and thus the energy required depends on three things:
- the height of the second floor (the distance \(d\));
- your mass, which must be raised that distance against the downward acceleration due to gravity; and
- your path.
Pressure-Volume (PV) Work
To describe this pressure–volume work (PV work), we will use such imaginary oddities as frictionless pistons, which involve no component of resistance, and ideal gases, which have no attractive or repulsive interactions. Imagine, for example, an ideal gas, confined by a frictionless piston, with internal pressure \(P_{int}\) and initial volume \(V_i\) (Figure \(\PageIndex{6}\)). If \(P_{ext} = P_{int}\), the system is at equilibrium; the piston does not move, and no work is done. If the external pressure on the piston (\(P_{ext}\)) is less than \(P_{int}\), however, then the ideal gas inside the piston will expand, forcing the piston to perform work on its surroundings; that is, the final volume (\(V_f\)) will be greater than \(V_i\). If \(P_{ext} > P_{int}\), then the gas will be compressed, and the surroundings will perform work on the system.
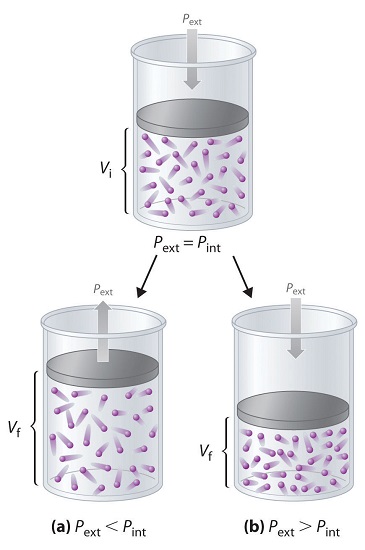
Figure \(\PageIndex{6}\): PV Work demonstrated with a frictionless piston. (a) if the external pressure is less than \(P_{int}\), the ideal gas inside the piston will expand, forcing the piston to perform work on its surroundings. The final volume (\(V_f\)) will be greater than \(V_i\). (b) Alternatively, if the external pressure is greater than \(P_{int}\), the gas will be compressed, and the surroundings will perform work on the system.
If the piston has cross-sectional area \(A\), the external pressure exerted by the piston is, by definition, the force per unit area:
\[P_{ext} = \dfrac{F}{A} \label{eq5}\]
The volume of any three-dimensional object with parallel sides (such as a cylinder) is the cross-sectional area times the height (\(V = Ah\)). Rearranging Equation \ref{eq5} to give
\[F = P_{ext}A\]
and defining the distance the piston moves (\(d\)) as \(Δh\), we can calculate the magnitude of the work performed by the piston by substituting into Equation \(\ref{12.3.1}\):
\[w = F d = P_{ext}AΔh \label{12.3.3}\]
The change in the volume of the cylinder (\(ΔV\)) as the piston moves a distance d is \(ΔV = AΔh\), as shown in Figure \(\PageIndex{7}\).
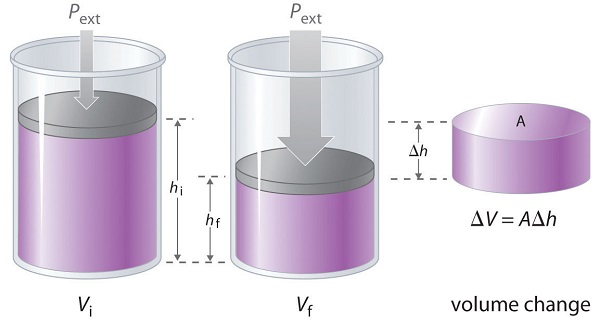
Figure \(\PageIndex{7}\): Work Performed with a change in volume. The change in the volume (\(ΔV\)) of the cylinder housing a piston is \(ΔV = AΔh\) as the piston moves. The work performed by the surroundings on the system as the piston moves inward is given by Equation \ref{12.3.4}.
The PV work performed is thus
\[ w = P_{ext}ΔV \label{12.3.4}\]
The units of work obtained using this definition are correct for energy: pressure is force per unit area (newton/m2) and volume has units of cubic meters, so
If we use atmospheres for P and liters for V, we obtain units of L·atm for work. These units correspond to units of energy, as shown in the different values of the ideal gas constant R:
\[R=\dfrac{0.08206\;\mathrm{L\cdot atm}}{\mathrm{mol\cdot K}}=\dfrac{8.314\textrm{ J}}{\mathrm{mol\cdot K}}\]
Thus 0.08206 L·atm = 8.314 J and 1 L·atm = 101.3 J.
Exercise: Expansion (PV) work
- How much work is done by a gas that expands from 2 liters to 5 liters against an external pressure of 750 mmHg?
- How much work is done by 0.54 moles of a gas that has an initial volume of 8 liters and expands under the following conditions: 30 oC and 1.3 atm?
- How much work is done by a gas (P=1.7 atm, V=1.56 L) that expands against an external pressure of 1.8 atm?
- Solution a
-
\[w = − PΔV\]
\[ΔV = V_{final} - V_{Initial} = 5 \,L - 2\, L = 3 L\]
Convert 750 mmHg to atm:
\[750 mmHg * 1/760 (atm/mmHg) = 0.9868 atm.\]
\[W = − pΔV = -(.9868\, atm)(3\,L) = -2.96 \,L\, atm.\]
- Solution b
-
First we must find the final volume using the ideal gas law:
\[pV = nRT\]
or
\[V = \dfrac{nRT}{P} = \dfrac{ [(0.54 \,moles)(0.082057 (L\, atm)/ (mol\, K))(303\,K)] }{1.3\, atm} = 10.33\, L\]
\[ΔV = V_{final} - V_{initial} = 10.3\, L - 8\, L = 2.3\, L\]
\[w = − pΔV = - (1.3\, atm)(2.3 \,L) = -3\, L\, atm.\]
- Solution c
-
\[w = - p * ΔV\) = - (1.8 \,atm )\, ΔV.\]
Given \(p_1\), \(V_1\), and \(p_2\), find \(V_2\): \(p_1V_1=p_2V_2\) (at constant \(T\) and \(n\))
\(V_2= (V_1* P_1) / P_2\) = (1.56 L * 1.7 atm) / 1.8 atm = 1.47 L
Now,
\[ΔV = V_2 - V_1=1.47\, L - 1.56\, L = -0.09\]
\[w = - (1.8 atm) * (-0.09 L) = 0.162 L atm.\]
Whether work is defined as having a positive sign or a negative sign is a matter of convention. Heat flow is defined from a system to its surroundings as negative; using that same sign convention, we define work done by a system on its surroundings as having a negative sign because it results in a transfer of energy from a system to its surroundings. This is an arbitrary convention and one that is not universally used. Some engineering disciplines are more interested in the work done on the surroundings than in the work done by the system and therefore use the opposite convention. Because ΔV > 0 for an expansion, Equation \(\ref{12.3.4}\) must be written with a negative sign to describe PV work done by the system as negative:
\[ w = −P_{ext}ΔV \label{12.3.5}\]
The work done by a gas expanding against an external pressure is therefore negative, corresponding to work done by a system on its surroundings. Conversely, when a gas is compressed by an external pressure, ΔV < 0 and the work is positive because work is being done on a system by its surroundings.
A Matter of Convention
- Heat flow is defined from the system to its surroundings as negative
- Work is defined as by the system on its surroundings as negative
Suppose, for example, that the system under study is a mass of steam heated by the combustion of several hundred pounds of coal and enclosed within a cylinder housing a piston attached to the crankshaft of a large steam engine. The gas is not ideal, and the cylinder is not frictionless. Nonetheless, as steam enters the engine chamber and the expanding gas pushes against the piston, the piston moves, so useful work is performed. In fact, PV work launched the Industrial Revolution of the 19th century and powers the internal combustion engine on which most of us still rely for transportation.
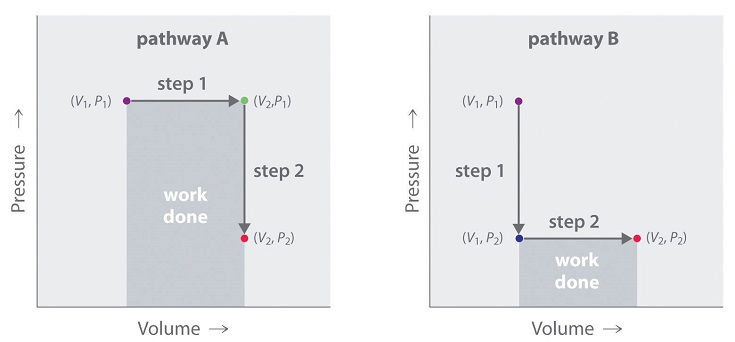
In contrast to internal energy, work is not a state function. We can see this by examining Figure \(\PageIndex{8}\), in which two different, two-step pathways take a gaseous system from an initial state to a final state with corresponding changes in temperature. In pathway A, the volume of a gas is initially increased while its pressure stays constant (step 1); then its pressure is decreased while the volume remains constant (step 2). In pathway B, the order of the steps is reversed. The temperatures, pressures, and volumes of the initial and final states are identical in both cases, but the amount of work done, indicated by the shaded areas in the figure, is substantially different. As we can see, the amount of work done depends on the pathway taken from (\(V_1\), \(P_1\)) to (\(V_2\), \(P_2\)), which means that work is not a state function.
Internal energy is a state function, whereas work is not.
Example \(\PageIndex{1}\): Internal Combustion Engine
A small high-performance internal combustion engine has six cylinders with a total nominal displacement (volume) of 2.40 L and a 10:1 compression ratio (meaning that the volume of each cylinder decreases by a factor of 10 when the piston compresses the air–gas mixture inside the cylinder prior to ignition). How much work in joules is done when a gas in one cylinder of the engine expands at constant temperature against an opposing pressure of 40.0 atm during the engine cycle? Assume that the gas is ideal, the piston is frictionless, and no energy is lost as heat.
Given: final volume, compression ratio, and external pressure
Asked for: work done
- Strategy:
-
Calculate the final volume of gas in a single cylinder. Then compute the initial volume of gas in a single cylinder from the compression ratio. Use Equation \(\ref{12.3.5}\) to calculate the work done in liter-atmospheres. Convert from liter-atmospheres to joules.
- Solution:
-
A To calculate the work done, we need to know the initial and final volumes. The final volume is the volume of one of the six cylinders with the piston all the way down: Vf = 2.40 L/6 = 0.400 L. With a 10:1 compression ratio, the volume of the same cylinder with the piston all the way up is Vi = 0.400 L/10 = 0.0400 L. Work is done by the system on its surroundings, so work is negative.
\[\begin{align} w &= −P_{ext}ΔV \nonumber \\[4pt] &= −(40.0\, atm)(0.400\, L − 0.0400 \,L) \nonumber \\[4pt] &= −14.4\, L·atm \nonumber \end{align} \nonumber\]
Converting from liter-atmospheres to joules,
\[\begin{align} w &=-(14.4\;\mathrm{L\cdot atm})[101.3\;\mathrm{J/(L\cdot atm)}] \nonumber \\[4pt] &= -1.46\times10^3\textrm{ J} \nonumber \end{align} \nonumber\]In the following exercise, you will see that the concept of work is not confined to engines and pistons. It is found in other applications as well.
Exercise \(\PageIndex{1}\): Work to Breath
Breathing requires work, even if you are unaware of it. The lung volume of a 70 kg man at rest changed from 2200 mL to 2700 mL when he inhaled, while his lungs maintained a pressure of approximately 1.0 atm. How much work in liter-atmospheres and joules was required to take a single breath? During exercise, his lung volume changed from 2200 mL to 5200 mL on each in-breath. How much additional work in joules did he require to take a breath while exercising?
- Answer
-
−0.500 L·atm, or −50.7 J; −304 J; if he takes a breath every three seconds, this corresponds to 1.4 Calories per minute (1.4 kcal).
Work and Chemical Reactions
We have stated that the change in energy (\(ΔU\)) is equal to the sum of the heat produced and the work performed. Work done by an expanding gas is called pressure-volume work, (or just PV work). Consider, for example, a reaction that produces a gas, such as dissolving a piece of copper in concentrated nitric acid. The chemical equation for this reaction is as follows:
\[Cu_{(s)} + 4HNO_{3(aq)} \rightarrow Cu(NO_3)_{2(aq)} + 2H_2O_{(l)} + 2NO_{2(g)} \label{12.3.5a}\]
If the reaction is carried out in a closed system that is maintained at constant pressure by a movable piston, the piston will rise as nitrogen dioxide gas is formed (Figure \(\PageIndex{9}\)). The system is performing work by lifting the piston against the downward force exerted by the atmosphere (i.e., atmospheric pressure). We find the amount of PV work done by multiplying the external pressure P by the change in volume caused by movement of the piston (ΔV). At a constant external pressure (here, atmospheric pressure)
\[w = −PΔV \label{12.3.6}\]
The negative sign associated with \(PV\) work done indicates that the system loses energy. If the volume increases at constant pressure (ΔV > 0), the work done by the system is negative, indicating that a system has lost energy by performing work on its surroundings. Conversely, if the volume decreases (ΔV < 0), the work done by the system is positive, which means that the surroundings have performed work on the system, thereby increasing its energy.

The symbol \(U\) represents the internal energy of a system, which is the sum of the kinetic energy and potential energy of all its components. It is the change in internal energy that produces heat plus work. To measure the energy changes that occur in chemical reactions, chemists usually use a related thermodynamic quantity called enthalpy (H) (from the Greek enthalpein, meaning “to warm”). The enthalpy of a system is defined as the sum of its internal energy \(U\) plus the product of its pressure \(P\) and volume \(V\):
\[H =U + PV \label{12.3.7}\]
Because internal energy, pressure, and volume are all state functions, enthalpy is also a state function.
If a chemical change occurs at constant pressure (i.e., for a given P, ΔP = 0), the change in enthalpy (ΔH) is
\[ ΔH = Δ(U + PV) = ΔU + ΔPV = ΔU + PΔV \label{12.3.8}\]
Substituting \(q + w\) for \(ΔU\) (Equation \(\ref{12.3.8}\)) and \(−w\) for \(PΔV\) (Equation \(\ref{12.3.6}\)), we obtain
\[ΔH = ΔU + PΔV = q_p + w − w = q_p \label{12.3.9}\]
The subscript \(p\) is used here to emphasize that this equation is true only for a process that occurs at constant pressure. From Equation \(\ref{12.3.9}\) we see that at constant pressure the change in enthalpy, \(ΔH\) of the system, defined as \(H_{final} − H_{initial}\), is equal to the heat gained or lost.
\[ΔH = H_{final} − H_{initial} = q_p \label{12.3.10}\]
Just as with \(ΔU\), because enthalpy is a state function, the magnitude of \(ΔH\) depends on only the initial and final states of the system, not on the path taken. Most important, the enthalpy change is the same even if the process does not occur at constant pressure.
To find \(ΔH\) for a reaction, measure \(q_p\) under constant pressure.
Summary
All forms of energy can be interconverted. Three things can change the energy of an object: the transfer of heat, work performed on or by an object, or some combination of heat and work.
Outside Links
- Gasparro, Frances P. "Remembering the sign conventions for q and w in deltaU = q - w." J. Chem. Educ. 1976: 53, 389.
- Koubek, E. "PV work demonstration (TD)." J. Chem. Educ. 1980: 57, 374. '

