1.10: Blackbody Radiation
- Page ID
- 70542
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)CHEM 174 Physical Chemistry Laboratory II
Blackbody Radiation
Classical mechanics failed as scientists examined nature on smaller and smaller spatial scales. There where five experimental observations that were of particular importance for the development of quantum mechanics.
First Experiments that Established Quantum Mechanics
- Blackbody Radiation
- Photoelectric Effect
- Atomic and Molecular Spectroscopy
- Heat Capacities at Low Temperature
- Electron Diffraction
Blackbody radiation was one of the first experiments that lead to quantum mechanics. It started with the simple observation that when you heat a metal that it first becomes red, followed by yellow and then white hot as the temperature increases. Now, imagine a cube with a tiny pinhole that leads to a very irregular cavity inside the cube. As the Figure 1 shows, any light reaching the pinhole is very likely to be absorbed before it can exit the pinhole.
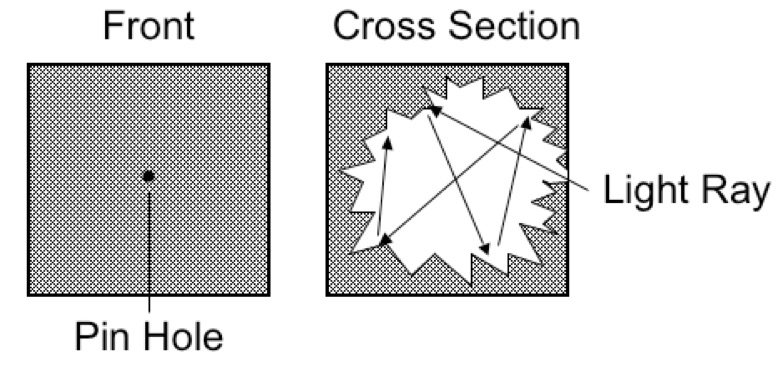
Figure 1. An idealized blackbody radiator
Any object in thermal equilibrium is constantly emitting and absorbing radiation. Kirchhoff’s Law states that a body that radiates strongly at some wavelength also absorbs radiation strongly at the same wavelength. Therefore an ideal blackbody radiator is both a perfect absorber and emitter of radiation. Many thermal sources, such as the sun, a flame, an incandescent light bulb, the Earth, approximate blackbody radiators. However, if you use only classical physics, the radiation from a blackbody radiator is impossible to describe correctly without quantum mechanics.
Careful measurements that used experimental approximations to the ideal blackbody radiator showed that the radiation distribution depends only on the temperature of the body. The hotter the temperature the greater the radiation and the lower the wavelength of the peak, Figure 2.
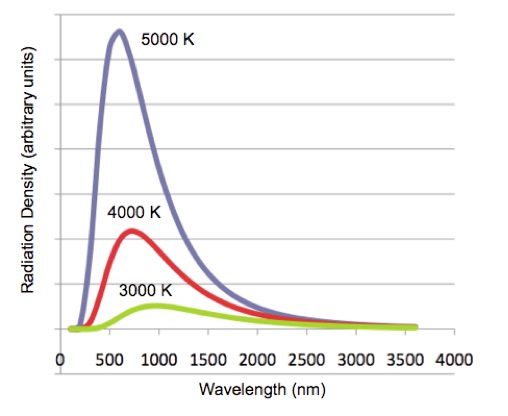
Figure 2. Blackbody radiation for three different temperatures.
The radiation distribution B(T) is:
Equation (1)
\[B_{\lambda}\left ( T \right )=\frac{3.74\times 10 ^{^{-16}}\lambda ^{-5 }}{\pi\left ( \exp \left ( 1.45\times 10 ^{-2}/\left ( \lambda T \right ) \right )-1 \right ) } \nonumber \]
The radiation peak, λmax, is equal to:
Equation (2)
\[\lambda _{max}(nm)=\frac{2.897\times 10^{6}\left ( nmK \right )}{T\left ( K \right )} \nonumber \]
For a blackbody the power emitted per unit area, M, is:
Equation (3)
\[M=\sigma T^{4} \nonumber \] \[\sigma =5.67\times 10^{-8}Wm^{-2}K^{-4} \nonumber \]
A first attempt to explain these observations was made by Lord Rayleigh. He assumed that the thermal motions of atoms that compose the walls of the blackbody excite “oscillators” of the electromagnetic field. (For a very rough mental picture of his oscillators, think of the electromagnetic field as a vast series of strings on a musical instrument.) Next he applied the equipartition principle from statistical thermodynamics. The assumption was that all of the oscillators share equally in the energy supplied by the walls. According to the equipartition principle each oscillator gets kinetic energy of ½ kT and potential energy of ½ kT for a total of kT where: k is Boltzmann’s Constant (the gas constant divided by Avogadro's number and the temperature, T. Even the oscillators with the highest frequencies such as x-rays and even more are excited. This reasoning led to the Rayleigh-Jeans Law where σ is the radiation density:
Equation (4)
\[dE=\delta d\lambda \nonumber \] \[\delta =\frac{8\pi kT}{\lambda ^{4}} \nonumber \]
The accumulation of energy in the highest frequencies leads to a severe problem with the Rayleigh-Jeans Law. As the wavelength gets shorter that amount of radiation becomes greater and greater, Figure 3. Everything in this world glows in the dark according to the Rayleigh-Jeans Law. If it were not for quantum effects a lighted match should emit x-rays intensely and even more gamma-rays! This incorrect prediction is called the “ultraviolet catastrophe.”

Figure 3. The ultraviolet catastrophe predicted by the Rayleigh-Jeans Law
The ultraviolet catastrophe makes no sense! Max Planck solved the problem by assuming that the energy appears in discreet (quantized) packages. He assumed that the energy, E, of an oscillator was equal to an integer multiplied by a constant, h (Planck’s constant), times the frequency of the oscillator.
Equation (5)
\[E=nh\nu \nonumber \] \[n=0,1,2,3... \nonumber \]
If Equation 5 is correct than oscillators are excited only if they can get energy of at least kT. But as the frequency ν becomes greater it becomes more difficult for an oscillator to receive enough energy from the blackbody’s walls. The maximum oscillator frequency excited depends only on the temperature of the walls. The net effect of assuming that energy is quantized eliminates the contribution of high-frequency oscillators to the emitted radiation and this eliminates the ultraviolet catastrophe. The blackbody radiation predicted from the quantum theory of Max Planck conforms to Equations 1 – 3.
In this laboratory you will investigate the effect of temperature on the location of the peak of the blackbody radiation curve.
Procedure
Required Equipment
Ocean Optics UV-Vis Spectrometer
Blackbody Radiator Experimental Setup
Candle
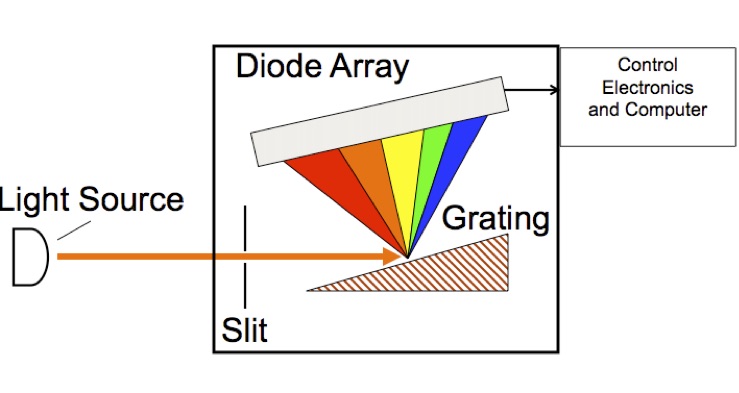
Figure 4. Schematic diagram of Ocean Optics UV-Vis spectrometer
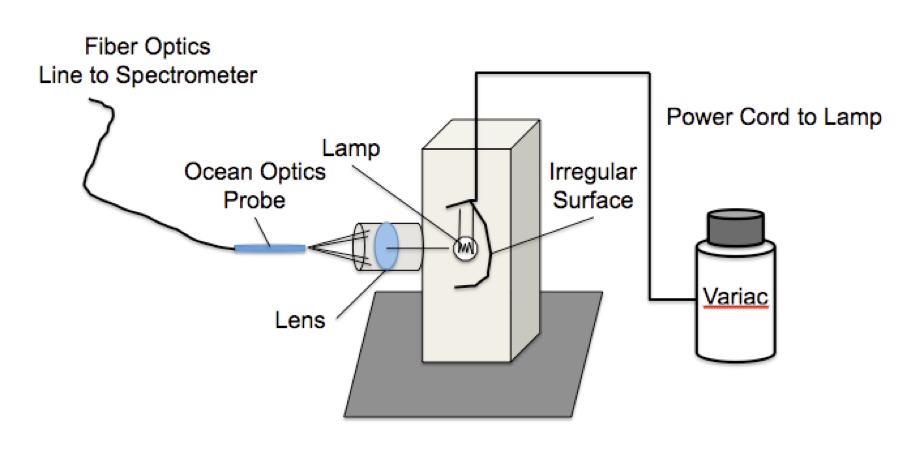
Figure 5. Blackbody radiator experimental setup
Blackbody Radiation Measurements
The procedure is to make at observations of the emission spectrum of the light emitted from the blackbody radiation setup with the Ocean Optics UV-Vis Spectrometer. Vary the setting of the power Variac and take spectra.
Candle Radiation Measurements
The procedure is to make at observations of the emission spectrum of the light emitted from a candle flame with the Ocean Optics UV-Vis Spectrometer. Take spectra of different sections of the flame (lower blue, middle, upper most…). Be careful, do not put the lens of the optical probe in the candle flame.
Calculations
- Use the calibration equations given in class to correct the measured wavelength scale using the calibration equation that you got from the calibration laboratory to get the true wavelengths for the blackbody and candle spectra.
- Plot each of the blackbody radiation spectra. The x-axis will be the true wavelength in nm and the y-axis will be emission intensity.
- Determine the peak of the radiation distribution, λmax, for all your spectra.
- Plot the peak of the radiation distribution, λmax, as a function of the variac setting.
- Use Equation (2) to calculate the temperature of the blackbody for each variac setting. Plot the temperature (y-axis) as a function of the variac setting (x-axis).
- Taking the temperatures calculated in step 5, use Equation (3) to calculate the power per unit area emitted by the blackbody for each variac setting. Plot the power per unit area (y-axis) as a function of the variac setting (x-axis).
- Discuss your blackbody results in view of Equation (1).
- Use the blackbody equations to estimate the temperature of the various sections of the flame.
-
Report
Please follow the standard format for a scientific paper given in the syllabus and discussed in lecture. It includes the following.
- Abstract – A summery of the entire experiment
- Short Introduction describing the purpose and any relevant theory you find.
- Experimental with a short description of the apparatus and procedures.
- Results please tabulate your observations.
- Discussion and Conclusions Can you find other relevant observations? Compare your results with other available observations. Please discuss the answers to the questions (below) here.
- References. Cite all sources including books, peer reviewed journals and the internet. I am happiest when you find more than two.
- Appendix with a photocopy of the raw data as you entered them in your notebook. I do not need copies of all the spectrometer data, an example first page of one spectrum would be good (total 1 page).
Reference
- Atkins, P. and J. De Paula, Physical Chemistry, Eighth Edition W. H. Freeman, 2006.

