4: Titrations

Last updated

Jun 7, 2019
Save as PDF
- 3: Conjugate Acid-Base Pairs and pH
- 4.7-4.8

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$ $\newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$ $\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$ $\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$ $\newcommand{\AA}{\unicode[.8,0]{x212B}}$

$\newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vectorC}[1]{\textbf{#1}}$

$\newcommand{\vectorD}[1]{\overrightarrow{#1}}$

$\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}$

$\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}$

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\avec}{\mathbf a}$

$\newcommand{\bvec}{\mathbf b}$

$\newcommand{\cvec}{\mathbf c}$

$\newcommand{\dvec}{\mathbf d}$

$\newcommand{\dtil}{\widetilde{\mathbf d}}$

$\newcommand{\evec}{\mathbf e}$

$\newcommand{\fvec}{\mathbf f}$

$\newcommand{\nvec}{\mathbf n}$

$\newcommand{\pvec}{\mathbf p}$

$\newcommand{\qvec}{\mathbf q}$

$\newcommand{\svec}{\mathbf s}$

$\newcommand{\tvec}{\mathbf t}$

$\newcommand{\uvec}{\mathbf u}$

$\newcommand{\vvec}{\mathbf v}$

$\newcommand{\wvec}{\mathbf w}$

$\newcommand{\xvec}{\mathbf x}$

$\newcommand{\yvec}{\mathbf y}$

$\newcommand{\zvec}{\mathbf z}$

$\newcommand{\rvec}{\mathbf r}$

$\newcommand{\mvec}{\mathbf m}$

$\newcommand{\zerovec}{\mathbf 0}$

$\newcommand{\onevec}{\mathbf 1}$

$\newcommand{\real}{\mathbb R}$

$\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$

$\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$

$\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$

$\newcommand{\laspan}[1]{\text{Span}\{#1\}}$

$\newcommand{\bcal}{\cal B}$

$\newcommand{\ccal}{\cal C}$

$\newcommand{\scal}{\cal S}$

$\newcommand{\wcal}{\cal W}$

$\newcommand{\ecal}{\cal E}$

$\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$

$\newcommand{\gray}[1]{\color{gray}{#1}}$

$\newcommand{\lgray}[1]{\color{lightgray}{#1}}$

$\newcommand{\rank}{\operatorname{rank}}$

$\newcommand{\row}{\text{Row}}$

$\newcommand{\col}{\text{Col}}$

$\renewcommand{\row}{\text{Row}}$

$\newcommand{\nul}{\text{Nul}}$

$\newcommand{\var}{\text{Var}}$

$\newcommand{\corr}{\text{corr}}$

$\newcommand{\len}[1]{\left|#1\right|}$

$\newcommand{\bbar}{\overline{\bvec}}$

$\newcommand{\bhat}{\widehat{\bvec}}$

$\newcommand{\bperp}{\bvec^\perp}$

$\newcommand{\xhat}{\widehat{\xvec}}$

$\newcommand{\vhat}{\widehat{\vvec}}$

$\newcommand{\uhat}{\widehat{\uvec}}$

$\newcommand{\what}{\widehat{\wvec}}$

$\newcommand{\Sighat}{\widehat{\Sigma}}$

$\newcommand{\lt}{<}$

$\newcommand{\gt}{>}$

$\newcommand{\amp}{&}$

$\definecolor{fillinmathshade}{gray}{0.9}$

A titration is a volumetric technique in which a solution of one reactant (the titrant) is added to a solution of a second reactant (the "analyte") until the equivalence point is reached. The equivalence point is the point at which titrant has been added in exactly the right quantity to react stoichiometrically with the analyten (when moles of titrant = moles of analyte). If either the titrant or analyte is colored, the equivalence point is evident from the disappearance of color as the reactants are consumed. Otherwise, an indicator may be added which has an "endpoint" (changes color) at the equivalence point, or the equivalence point may be determined from a titration curve. The amount of added titrant is determined from its concentration and volume:

n (mol) = C (mol/L) * V (L)

and the amount of titrant can be used in the usual stoichiometric calculation to determine the amount of analyte.

The titration process can be observed in the video below.

A measured volume of the solution to be titrated, in this case, colorless aqueous acetic acid, CH₃COOH(aq) is placed in a beaker. The colorless sodium hydroxide NaOH(aq), which is the titrant, is added carefully by means of a buret. The volume of titrant added can then be determined by reading the level of liquid in the buret before and after titration. This reading can usually be estimated to the nearest hundredth of a milliliter, so precise additions of titrant can be made rapidly.

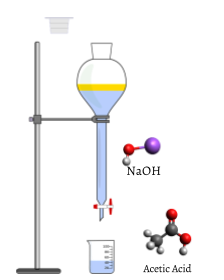
3.12_pre_addition_titration.png

Figure $\PageIndex{1}$ :The titration setup initially, before titrant (NaOH) has been added. NaOH is held in the burett, which is positioned above the beaker of acetic acid. Titrant (NaOH) is added until it neutralizes all of the analyte (acetic acid). This is called the equivalence point. Note: Unlike the picture, both substances are actually clear but are blue for visibility purposes in the picture.

As the first few milliliters of titrant flow into the flask, some indicator briefly changes to pink, but returns to colorless rapidly. This is due to a large excess of acetic acid. The limiting reagent NaOH is entirely consumed.

The added indicator changes to pink when the titration is complete, indicating that all of the aqueous acetic acid has been consumed by NaOH(aq). The reaction which occurs is

$\text{C} \text{H}_{3} \text{COOH} (aq) + \text{ NaOH} (aq) \rightarrow \text{ Na}^{+} (aq) + \text{CH}_{3} \text{COO}^{-} (aq) + \text{H}_{2} \text{O} (l) \label{2}$

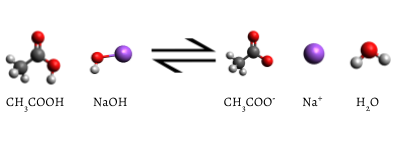
3.12_Acetic_Acid_reaction.png

Eventually, all the acetic acid is consumed. Addition of even a fraction of a drop of titrant produces a lasting pink color due to unreacted NaOH in the flask. The color change that occurs at the endpoint of the indicator signals that all the acetic acid has been consumed, so we have reached the equivalence point of the titration. If slightly more NaOH solution were added, there would be an excess and the color of the solution in the flask would get much darker. The endpoint appears suddenly, and care must be taken not to overshoot the endpoint.

After the titration has reached the endpoint, a final volume is read from the buret. Using the initial and final reading, the volume added can be determined quite precisely:

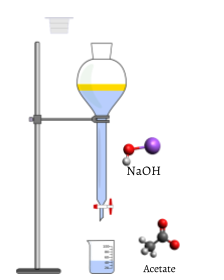
3.12_equivalence_point.png

Figure $\PageIndex{2}$ The figure above shows a completed titration, where the equivalence point has been reached. NaOH (the titrant) has neutralized all of the Acetic Acid, leaving Acetate in the beaker. At this point, the moles of NaOH added is equivalent to the moles of acetic acid initially in the beaker.

The object of a titration is always to add just the amount of titrant needed to consume exactly the amount of substance being titrated. In the NaOH—CH₃COOH reaction Eq. $\ref{2}$ , the equivalence point occurs when an equal molar amount of NaOH has been added from the graduated cylinder for every mole of CH₃COOH originally in the titration flask. That is, at the equivalence point the ratio of the amount of NaOH, added to the amount of CH₃COOH consumed must equal the stoichiometric ratio

$\dfrac{n_{\text{NaOH}}\text{(added from graduated cylinder)}}{n_{\text{CH}_{\text{3}}{\text{COOH}}}\text{(initially in flask)}}=\text{S}( \dfrac{\text{NaOH}}{\text{CH}_{\text{3}}\text{COOH}} )$

$=\dfrac{\text{1 mol NaOH}}{\text{1 mol CH}_{\text{3}}\text{COOH}}$

Example $\PageIndex{1}$ : Endpoint of Titration

What volume of 0.05386 M KMnO₄ would be needed to reach the endpoint when titrating 25.00 ml of 0.1272 M H₂O₂, given S(KMnO₄/H₂O₂) = 2/5

Solution

At the equivalence point, the stoichiometric ratio will apply, and we can use it to calculate the amount of KMnO₄ which must be added:

$n_{\text{KMnO}_{\text{4}}}\text{(added)}=n_{\text{H}_{\text{2}}\text{O}_{\text{2}}}\text{(in flask)}\times \text{S}\left( \dfrac{\text{KMnO}_{\text{4}}}{\text{H}_{\text{2}}\text{O}_{\text{2}}} \right)$

The amount of H₂O₂ is obtained from the volume and concentration:

$n_{\text{H}_{\text{2}}\text{O}_{\text{2}}}\text{(in flask)}=25.00\text{ cm}^{\text{3}}\times \text{0}\text{.1272 }\dfrac{\text{mmol}}{\text{cm}^{\text{3}}}=\text{3}\text{.180 mmol H}_{\text{2}}\text{O}_{\text{2}}$

Then

$n_{\text{KMnO}_{\text{4}}}\text{(added)}=\text{3}\text{.180 mmol H}_{\text{2}}\text{O}_{\text{2}}\times \dfrac{\text{2 mol KMnO}_{\text{4}}}{\text{5 mol H}_{\text{2}}\text{O}_{\text{2}}}\times \dfrac{\text{10}^{\text{-3}}}{\text{10}^{\text{-3}}}$

$=\text{3}\text{.180 mmol H}_{\text{2}}\text{O}_{\text{2}}\times \dfrac{\text{2 mmol KMnO}_{\text{4}}}{\text{5 mmol H}_{\text{2}}\text{O}_{\text{2}}}$

$= 1.272mmol KMnO 4$

To obtain V_KMnO4(aq) we use the concentration as a conversion factor:

$V_{\text{KMnO}_{\text{4}}\text{(}aq\text{)}}=\text{1}\text{.272 mmol KMnO}_{\text{4}}\times \dfrac{\text{1 cm}^{\text{3}}}{\text{5}\text{.386}\times \text{10}^{\text{-2}}\text{ mmol KMnO}_{\text{4}}}$

$= 23.62 cm 3$

Note that overtitrating [adding more than 23.62 cm³ of KMnO₄(aq) would involve an excess (more than 1.272 mmol) of KMnO₄.

Titration is often used to determine the concentration of a solution. In many cases it is not a simple matter to obtain a pure substance, weigh it accurately, and dissolve it in a volumetric flask as was done in Example 1 of Solution Concentrations. NaOH, for example, combines rapidly with H₂O and CO₂ from the air, and so even a freshly prepared sample of solid NaOH will not be pure. Its weight would change continuously as CO₂(g) and H₂O(g) were absorbed. Hydrogen chloride (HCl) is a gas at ordinary temperatures and pressures, making it very difficult to handle or weigh. Aqueous solutions of both of these substances must be standardized; that is, their concentrations must be determined by titration.

Example $\PageIndex{2}$ : Concentration of Titrant

A sample of pure potassium hydrogen phthalate (KHC₈H₄O₄) weighing 0.3421 g is dissolved in distilled water. Titration of the sample requires 27.03 ml NaOH(aq). The titration reaction is

$\text{NaOH} (aq) + \text{KHC}_{8} \text{H}_{4} \text{O}_{4} (aq) \rightarrow \text{NaKC}_{8} \text{H}_{4} \text{O}_{4} (aq) + \text{H}_{2} \text{O}$

What is the concentration of NaOH(aq) ?

Solution

To calculate concentration, we need to know the amount of NaOH and the volume of solution in which it is dissolved. The former quantity could be obtained via a stoichiometric ratio from the amount of KHC₈H₄O₄, and that amount can be obtained from the mass

$m_{\text{KHC}_{\text{8}}\text{H}_{\text{4}}\text{O}_{\text{4}}}\text{ }\xrightarrow{M_{\text{KHC}_{\text{8}}\text{H}_{\text{4}}\text{O}_{\text{4}}}}\text{ }n_{\text{KHC}_{\text{8}}\text{H}_{\text{4}}\text{O}_{\text{4}}}\text{ }\xrightarrow{S\text{(NaOH/KHC}_{\text{8}}\text{H}_{\text{4}}\text{O}_{\text{4}}\text{)}}\text{ }n_{\text{NaOH}}$

$n_{\text{NaOH}}=\text{3}\text{.180 g}\times \dfrac{\text{1 mol KHC}_{\text{8}}\text{H}_{\text{4}}\text{O}_{\text{4}}}{\text{204}\text{.22 g}}\times \dfrac{\text{1 mol NaOH}}{\text{1 mol KHC}_{\text{8}}\text{H}_{\text{4}}\text{O}_{\text{4}}}$

$=\text{1}\text{.674 }\times 10^{\text{-3}}\text{ mol NaOH}=\text{1}\text{.675 mmol NaOH}$

The concentration is

$c_{\text{NaOH}}=\dfrac{n_{\text{NaOH}}}{V}=\dfrac{\text{1}\text{.675 mmol NaOH}}{\text{27}\text{.03 cm}^{\text{3}}}=\text{0}\text{.06197 mmol cm}^{\text{-3}}$

or 0.06197 M.

By far the most common use of titrations is in determining unknowns, that is, in determining the concentration or amount of substance in a sample about which we initially knew nothing. The next example involves an unknown that many persons encounter every day.

Example $\PageIndex{3}$ : Vitamin C

Vitamin C tablets contain ascorbic acid (C₆H₈O₆) and a starch “filler” which holds them together. To determine how much vitamin C is present, a tablet can be dissolved in water andwith sodium hydroxide solution, NaOH(aq). The equation is

$\text{C}_{6} \text{H}_{8} \text{O}_{6} (aq) + \text{NaOH} (aq) \rightarrow \text{ Na C}_{6} \text{H}_{7} \text{O}_{6} (aq) + \text{H}_{2} \text{O} (l)$

If titration of a dissolved vitamin C tablet requires 16.85 cm³ of 0.1038 M NaOH, how accurate is the claim on the label of the bottle that each tablet contains 300 mg of vitamin C?

Solution

The known volume and concentration allow us to calculate the amount of NaOH(aq) which reacted with all the vitamin C. Using the stoichiometric ratio

$\text{S}\left( \dfrac{\text{C}_{\text{6}}\text{H}_{\text{8}}\text{O}_{\text{6}}}{\text{NaOH}} \right)=\dfrac{\text{1 mmol C}_{\text{6}}\text{H}_{\text{8}}\text{O}_{\text{6}}}{\text{1 mmol NaOH}}$

we can obtain the amount of C₆H₈O₆. The molar mass converts that amount to a mass which can be compared with the label. Schematically

$\begin{align} & V_{\text{NaOH}}\rightarrow{c_{\text{NaOH}}}n_{\text{NaOH}}\rightarrow{\text{S(C}_{\text{6}}\text{H}_{\text{8}}\text{O}_{\text{6}}\text{/NaOH)}}n_{\text{C}_{\text{6}}\text{H}_{\text{8}}\text{O}_{\text{6}}}\rightarrow{M_{\text{C}_{\text{6}}\text{H}_{\text{8}}\text{O}_{\text{6}}}}\text{m}_{\text{C}_{\text{6}}\text{H}_{\text{8}}\text{O}_{\text{6}}} \\ & \text{m}_{\text{C}_{\text{6}}\text{H}_{\text{8}}\text{O}_{\text{6}}}=\text{16}\text{.85 cm}^{\text{3}}\times \dfrac{\text{0}\text{.1038 mmol NaOH}}{\text{1 cm}^{\text{3}}}\times \dfrac{\text{1 mmol C}_{\text{6}}\text{H}_{\text{8}}\text{O}_{\text{6}}}{\text{1 mmol NaOH}}\times \dfrac{\text{176}\text{.1 mg }}{\text{mmol C}_{\text{6}}\text{H}_{\text{8}}\text{O}_{\text{6}}} \\ & = 308.0 \text{ mg} \end{align}$

Note that the molar mass of C₆H₈O₆

$\dfrac{\text{176}\text{.1 g }}{\text{1 mol C}_{\text{6}}\text{H}_{\text{8}}\text{O}_{\text{6}}}=\dfrac{\text{176}\text{.1 g }}{\text{1 mol C}_{\text{6}}\text{H}_{\text{8}}\text{O}_{\text{6}}}\times \dfrac{\text{10}^{\text{-3}}}{\text{10}^{\text{-3}}}$

$=\dfrac{\text{176}\text{.1 g}\times \text{10}^{\text{-3}}\text{ }}{\text{10}^{\text{-3}}\text{ mol C}_{\text{6}}\text{H}_{\text{8}}\text{O}_{\text{6}}}=\dfrac{\text{176}\text{.1 mg }}{\text{1 mmol C}_{\text{6}}\text{H}_{\text{8}}\text{O}_{\text{6}}}$

can be expressed in milligrams per millimole as well as in grams per mole.

The 308.0 mg obtained in this example is in reasonably close agreement with the manufacturer’s claim of 300 mg. The tablets are stamped out by machines, not weighed individually, and so some variation is expected.

Contributors

Ed Vitz (Kutztown University), John W. Moore (UW-Madison), Justin Shorb (Hope College), Xavier Prat-Resina (University of Minnesota Rochester), Tim Wendorff, and Adam Hahn.

Search

Text Color

Text Size

Margin Size

Font Type

Contributors Ed Vitz (Kutztown University), John W. Moore (UW-Madison), Justin Shorb (Hope College), Xavier Prat-Resina (University of Minnesota Rochester), Tim Wendorff, and Adam Hahn.

Support Center

How can we help?

Contributors

Ed Vitz (Kutztown University), John W. Moore (UW-Madison), Justin Shorb (Hope College), Xavier Prat-Resina (University of Minnesota Rochester), Tim Wendorff, and Adam Hahn.