17.2: Molar Solubility and Ksp
- Page ID
- 55076
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Relating Solubilities to Solubility Constants
The solubility (by which we usually mean the molar solubility) of a solid is expressed as the concentration of the "dissolved solid" in a saturated solution. In the case of a simple 1:1 solid such as AgCl, this would just be the concentration of Ag+ or Cl– in the saturated solution. But for a more complicated stoichiometry such as as silver chromate, the solubility would be only one-half of the Ag+ concentration.
For example, let us denote the solubility of Ag2CrO4 as S mol L–1. Then for a saturated solution, we have
- \([Ag^+] = 2S\)
- \( [CrO_4^{2–}] = S\)
Substituting this into Eq 5b above,
\[(2S)^2 (S) = 4S^3 = 2.76 \times 10^{–12}\]
\[S= \left( dfrac{K_{sp}}{4} \right)^{1/3} = (6.9 \times 10^{-13})^{1/3} = 0.88 \times 10^{-4} \label{6a}\]
thus the solubility is \(8.8 \times 10^{–5}\; M\).
Note that the relation between the solubility and the solubility product constant depends on the stoichiometry of the dissolution reaction. For this reason it is meaningless to compare the solubilities of two salts having the formulas A2B and AB2, say, on the basis of their Ks values.
Note
It is meaningless to compare the solubilities of two salts having different formulas on the basis of their Ks values.
Example \(\PageIndex{2}\)
The solubility of CaF2 (molar mass 78.1) at 18°C is reported to be 1.6 mg per 100 mL of water. Calculate the value of Ks under these conditions.
Solution
moles of solute in 100 mL; S = 0.0016 g / 78.1 g/mol = \(2.05 \times 10^{-5}\) mol
\[S = \dfrac{2.05 \times 10^{ –5} mol}{0.100\; L} = 2.05 \times 10^{-4} M\]
\[K_{sp}= [Ca^{2+}][F^–]^2 = (S)(2S)^2 = 4 × (2.05 \times 10^{–4})^3 = 3.44 \times 10^{–11}\]
Example \(\PageIndex{3}\)
Estimate the solubility of La(IO3)3 and calculate the concentration of iodate in equilibrium with solid lanthanum iodate, for which Ks = 6.2 × 10–12.
Solution
The equation for the dissolution is
\[La(IO_3)_3 \rightleftharpoons La^{3+ }+ 3 IO_3^–\]
If the solubility is S, then the equilibrium concentrations of the ions will be
[La3+] = S and [IO3–] = 3S. Then Ks = [La3+][IO3–]3 = S(3S)3 = 27S4
27S4 = 6.2 × 10–12, S = ( ( 6.2 ÷ 27) × 10–12 )¼ = 6.92 × 10–4 M
[IO3–] = 3S = 2.08 × 10–5 (M)
Example \(\PageIndex{4}\): Cadmium
Cadmium is a highly toxic environmental pollutant that enters wastewaters associated with zinc smelting (Cd and Zn commonly occur together in ZnS ores) and in some electroplating processes. One way of controlling cadmium in effluent streams is to add sodium hydroxide, which precipitates insoluble Cd(OH)2 (Ks = 2.5E–14). If 1000 L of a certain wastewater contains Cd2+ at a concentration of 1.6E–5 M, what concentration of Cd2+ would remain after addition of 10 L of 4 M NaOH solution?
Solution
As with most real-world problems, this is best approached as a series of smaller problems, making simplifying approximations as appropriate.
Volume of treated water: 1000 L + 10 L = 1010 L
Concentration of OH– on addition to 1000 L of pure water:
(4 M) × (10 L)/(1010 L) = 0.040 M
Initial concentration of Cd2+ in 1010 L of water:
\[(1.6 \times 10^{–5}\; M) \left( \dfrac{100}{101} \right) \approx 1.6 \times 10^{–5}\; M\]
The easiest way to tackle this is to start by assuming that a stoichiometric quantity of Cd(OH)2 is formed — that is, all of the Cd2+ gets precipitated.
| Concentrations | [Cd2+], M | [OH–], M |
|---|---|---|
| initial | 1.6E–5 | 0.04 |
| change | –1.6E–5 | –3.2E–5 |
| final: | 0 | 0.04 – 3.2E–5 ≈ .04 |
Now "turn on the equilibrium" — find the concentration of Cd2+ that can exist in a 0.04M OH– solution:
| Concentrations | [Cd2+], M | [OH–], M |
|---|---|---|
| initial | o | 0.04 |
| change | +x | +2x |
| at equilibrium | x | .04 + 2x ≈ .04 |
Substitute these values into the solubility product expression:
Cd(OH)2(s) = [Cd2+] [OH–]2 = 2.5E–14
[Cd2+] = (2.5E–14) / (16E–4) = 1.6E–13 M
Note that the effluent will now be very alkaline: pH = 14 + log .04 = 12.6,
so in order to meet environmental standards an equivalent quantity of strong acid must be added to neutralize the water before it is released.
The Common Ion Effect
It has long been known that the solubility of a sparingly soluble ionic substance is markedly decreased in a solution of another ionic compound when the two substances have an ion in common. This is just what would be expected on the basis of the Le Châtelier Principle; whenever the process
\[CaF_{2(s)} \rightleftharpoons Ca^{2+} + 2 F^– \label{7}\]
is in equilibrium, addition of more fluoride ion (in the form of highly soluble NaF) will shift the composition to the left, reducing the concentration of Ca2+, and thus effectively reducing the solubility of the solid. We can express this quantitatively by noting that the solubility product expression
\[[Ca^{2+}][F^–]^2 = 1.7 \times 10^{–10} \label{8}\]
must always hold, even if some of the ionic species involved come from sources other than CaF2(s). For example, if some quantity x of fluoride ion is added to a solution initially in equilibrium with solid CaF2, we have
- \([Ca^{2+}] = S\)
- \([F^–] = 2S + x\)
so that
\[K_{sp} = [Ca^{2+}][ F^–]^2 = S (2S + x)^2 . \label{9a}\]
\[K_{sp} ≈ S x^2 \]
\[S = \dfrac{K_{sp}}{x^2} \label{9b}\]
The plots shown below illustrate the common ion effect for silver chromate as the chromate ion concentration is increased by addition of a soluble chromate such as Na2CrO4.
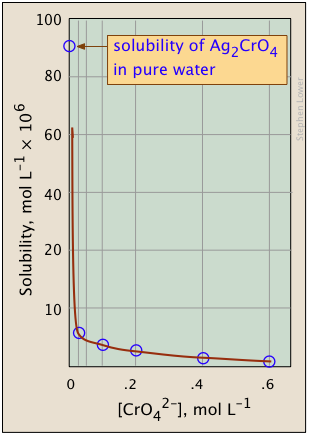
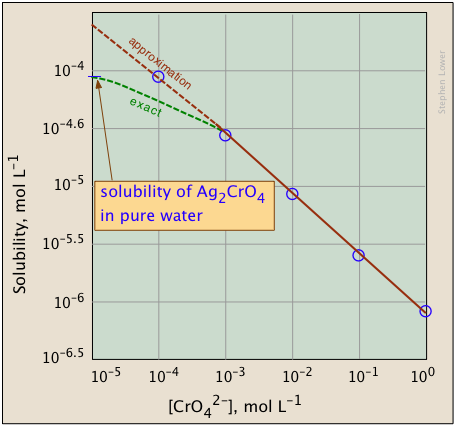
What's different about the plot on the right? If you look carefully at the scales, you will see that this one is plotted logarithmically (that is, in powers of 10.) Notice how a much wider a range of values can display on a logarithmic plot. The point of showing this pair of plots is to illustrate the great utility of log-concentration plots in equilibrium calculations in which simple approximations (such as that made in Equation \(\ref{9b}\) can yield straight-lines within the range of values for which the approximation is valid.
Example \(\PageIndex{5}\)
Calculate the solubility of strontium sulfate (Ks = 2.8 × 10–7) in (a) pure water and (b) in a 0.10 mol L–1 solution of Na2SO4.
Solution:
(a) In pure water, Ks = [Sr2+][SO42–] = S2
S = √Ks = (2.8 × 10–7)½ = 5.3 × 10–4
(b) In 0.10 mol L–1 Na2SO4, we have
Ks = [Sr2+][SO42–] = S × (0.10 + S) = 2.8 × 10–7
Because S is negligible compared to 0.10 M, we make the approximation
Ks = [Sr2+][SO42–] ≈ S × (0.10 M) = 2.8 × 10–7
so S ≈ (2.8 × 10–7) / 0.10M = 2.8 × 10–6 M — which is roughly 100 times smaller than the result from (a).

