7.9: Solubility: Introduction
- Page ID
- 213250
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Define solubility.
- Express the solubility limit of a solute as a proportion.
- State whether the solubility of a solid or a liquid solute is directly or indirectly proportional to its temperature.
- State whether the solubility of a gaseous solute is directly or indirectly proportional to its temperature.
As stated in Section 7.3, in order for a solution to form, the individual atoms or molecules of a solute must be dispersed among, and, therefore, exist in between, solvent particles. Since a specified volume of solvent contains a finite amount of space that can be occupied by solute particles, the quantity of solute that can be incorporated into a solution is limited by the amount of solvent in which it is dissolved. Therefore, in addition to evaluating the qualitative aspects of the substances that are utilized to prepare a solution, the relative quantities in which those chemicals are mixed must also be considered.
The solubility, which is also known as the solubility limit, of a solute corresponds to the maximum amount of that chemical that can dissolve in a given amount of solvent. Because, based on this definition, a solubility limit is a ratio of the amount of solute that can dissolve, relative to the quantity of solvent that is utilized to prepare the corresponding solution, solubilities are typically expressed as proportions, as shown below.
\( \dfrac{ \text{Maximum Amount of Solute}}{\text{Given Amount of Solvent}}\)
While the amount of a chemical that is contained in a solution can be expressed using any chemically-acceptable unit, the quantities within a solubility limit are typically reported using mass-based units, such as grams. However, as the solvents that are used to prepare liquid- and gas-phase solutions are often more easily quantified using volumetric measurements, the amount of solvent that is written in the denominator of a solubility proportion can also be recorded in milliliters, as shown below.
\( \dfrac{ \text{Maximum g Solute}}{\text{Given g Solvent}}\) or \( \dfrac{ \text{Maximum g Solute}}{\text{Given mL Solvent}}\)
Finally, in order to use these proportions to compare the solubilities of different solutes, chemists chose to perform all solubility experiments with solutions that were prepared using 100. grams, or 100. milliliters, of solvent. Because the amount of solvent that is reported in the denominator of a solubility proportion is a defined quantity, a solubility limit can be utilized to identify the solute and the solvent that are present in a particular solution. The role of a particular chemical can be assigned by analyzing the relative location in which that substance is written, or, alternatively, the numerical quantity with which that chemical is associated, in a solubility proportion. Based on the information that is provided above, the solvent is the substance that is reported as a 100.-gram, or 100.-milliliter, quantity in the denominator of a solubility limit, as shown below.
\( \dfrac{ \text{Maximum g Solute}}{100. \; \text{g Solvent}}\) or \( \dfrac{ \text{Maximum g Solute}}{100. \; \text{mL Solvent}}\)
The numerical value that corresponds to solubility of a solute, which is reported in the numerator of a solubility proportion, is dependent on several factors and, therefore, must be experimentally-determined. The composition of a chemical directly impacts its structure and three-dimensional shape, which, in turn, influence the distribution of electron density within that substance. Therefore, the identities of both the solute and the solvent alter the extent to which the solute particles can overcome the attractive forces that exist between the solvent molecules and, consequently, occupy the spaces that are generated as a result of these interactions. Since the amount of space that can be occupied by solute particles during the solvation process is directly proportional to the maximum amount of solute that can be dissolved in a solvent, the identity of both the solute and the solvent impact the solubility of the solute in the resulting solution.
Additionally, the temperature of a solution also impacts the quantity of solute that can be incorporated into a solvent during the solvation process. By increasing the temperature of a substance, its constituent particles are able to move more freely. As a result, solute particles are able to more easily overcome the attractive forces that exist between the solvent molecules and, therefore, temporarily generate "empty" spaces between those particles. Additionally, the solvent molecules that are contained in a solution also experience enhanced mobility at higher temperatures, which further increases the quantity of spatial voids that can be occupied by solute particles. Therefore, increasing the temperature of a solution causes solid and liquid solute particles to more rapidly disperse throughout and, consequently, occupy the spaces that are created in between, solvent particles. Since the amount of space that is occupied by solute particles during the solvation process impacts the maximum amount of solute that can be dissolved in a solvent, raising the temperature of a solution that contains a solid or a liquid solute increases the number of solute particles that can be dissolved in the resultant solution. Therefore, the solubility of a solid or a liquid solute is generally directly, or linearly, proportional to its temperature.
At higher temperatures, gaseous solute particles are also able to more easily overcome the attractive forces that exist between the solvent molecules. However, because gaseous chemicals exist as independent particles and, therefore, are inherently more mobile than solid or liquid particles, raising the temperature of a solution that contains a gaseous solute often causes the solute particles to completely dissociate from the solvent molecules and return to the gas phase, which decreases the number of solute particles that are dissolved in the resultant solution. Therefore, the solubility of a gaseous solute is generally indirectly, or inversely, proportional to its temperature.
The information that is described above can be visually-represented using a solubility curve, which graphs the experimentally-determined solubility of a solute as a function of its temperature. As shown Figure \(\PageIndex{1}\), raising the temperature of an aqueous solution that contains potassium iodide, KI, sodium nitrate, NaNO3, potassium nitrate, KNO3, ammonium chloride, NH4Cl, potassium chloride, KCl, sodium chloride, NaCl, or potassium chlorate, KClO3, increases the solubility of these solid solutes. In contrast, the solubilities of hydrogen chloride, HCl, nitrogen trihydride, NH3, and sulfur dioxide, SO2, which are all gaseous solutes, decrease as the temperature of the corresponding aqueous solution increases.
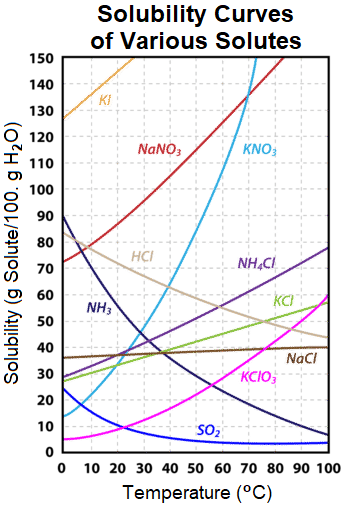
Table \(\PageIndex{1}\) lists the solubilities of several common ionic and covalent compounds at 20 degrees Celsius. The temperature at which these values were determined must be specified because, as stated above, the temperature of a solution impacts the quantity of solute that can be incorporated into a solvent during the solvation process.
| Solute | Solubility at 20 °C (g Solute/100. g of H2O) |
|---|---|
| Aluminum sulfate, Al2(SO4)3 | 36.4 |
| Ammonium iodide, NH4I | 172 |
| Calcium carbonate, CaCO3 | 6.17 × 10−4 |
| Carbon dioxide, CO2 | 0.178 |
| Fructose, C6H12O6 | 375 |
| Hydrogen sulfide, H2S | 0.33 |
| Iron (III) hydroxide, Fe(OH)3 | 2.10 × 10−9 |
| Lead (II) acetate, Pb(C2H3O2)2 | 44.3 |
| Lithium bromide, LiBr | 160. |
| Magnesium phosphate, Mg3(PO4)2 | 2.59 × 10−4 |
| Mercury (II) cyanide, Hg(CN)2 | 9.30 |
| Nickel (II) fluoride, NiF2 | 2.56 |
| Molecular oxygen, O2 | 9.110 × 10−4 |
| Potassium nitrate, KNO3 | 31.6 |
| Sodium chloride, NaCl | 35.9 |
| Urea, CO(NH2)2 | 108 |
Finally, because the chemical formula for water, H2O, is associated with the 100.-gram quantities in the denominators of the solubilities in both Figure \(\PageIndex{1}\) and Table \(\PageIndex{1}\), water is the solvent that was used to obtain all of the data that is presented above. As stated in Section 4.12, water is known as the "universal solvent," due to its ability to dissolve more substances than any other chemical. As a result, most solubility experiments that have been performed utilized solutions that were prepared by dissolving a solute in 100. grams, or 100. milliliters, of water.

