7.7: Solution Equations: Weak Electrolytes
- Page ID
- 222256
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Define weak electrolyte.
- Define recombination.
- Define equilibrium.
- Compare and contrast the definitions of non-, strong, and weak electrolytes.
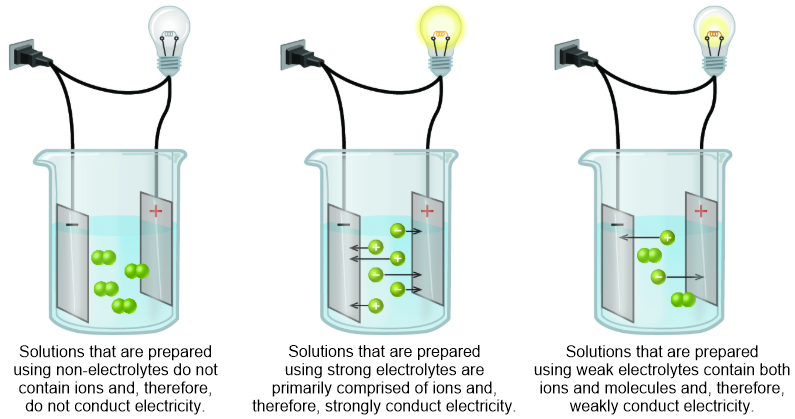
A weak electrolyte is a solute that partially dissociates, or separates, into its constituent cations and anions during the solvation process. However, the cations and anions that result from the solvation of a weak electrolyte experience strong electrostatic attractions and often recombine to regenerate the solute molecule from which they were produced. Therefore, solutions that are generated through the solvation of weak electrolytes contain both neutral molecules and ions. Because an electrical current can only flow between ions, the resultant homogeneous mixtures will weakly conduct an electrical current, as illustrated in the third image that is shown in Figure \(\PageIndex{1}\).
The dissociative behavior that is exhibited by a weak electrolyte is represented in the solution equation pattern that is shown below. Although a chemical change does not occur when a solution is formed, an arrow is used in a solution equation to indicate that solvation and, therefore, a physical change, has occurred. However, a standard "reaction" arrow, "\(\rightarrow\)," cannot be used to represent the solvation of a weak electrolyte, as this symbol indicates that transformations in the corresponding equation only occur in the "forward," or left-to-right, direction. As stated above, the cations and anions that result from the solvation of a weak electrolyte often recombine to regenerate the solute molecule from which they were produced. Therefore, the dissociation of weak electrolytes is reversible, and the arrow that is utilized to describe the recombination process must be oriented in the "backward," or right-to-left, direction in a solution equation. In order to indicate that the "forward" dissociation and "reverse" recombination processes occur simultaneously during the solvation of a weak electrolyte, an equilibrium arrow, "\(\rightleftharpoons\)," is incorporated into the solution equation for this type of solute.
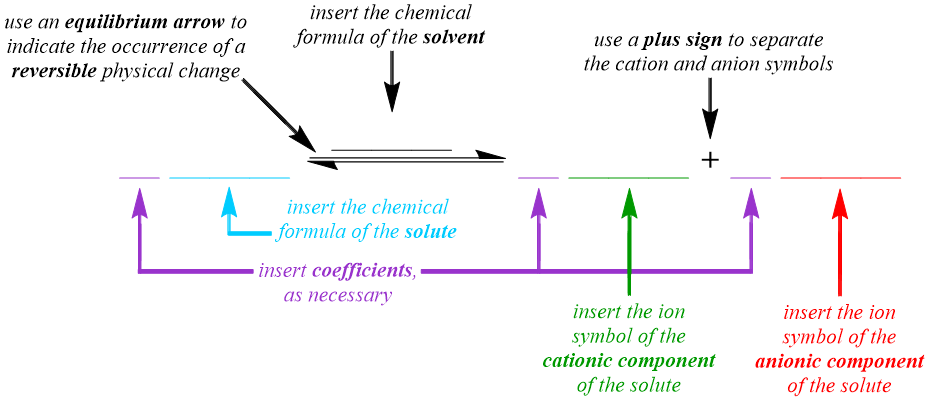
Because a solution equation is the symbolic representation of a physical change, the chemical formulas, not the chemical names, of the substances that are being transformed and created are incorporated into the pattern that is shown above. Since a solution equation is used to represent the electrolyte behavior of the chemical that is being dissolved, the chemical formula of the solute is written on the left side of the "reaction" arrow. A solution also contains a solvent, which does not undergo a physical change during the dissolving process and, therefore, does not exhibit any electrolyte behavior. As a result, the formula of the solvent should not be written on the left side of the "reaction" arrow. Instead, the chemical formula of the solvent is written over the "reaction" arrow, in order to indicate the presence of this substance in the resultant solution. Because a weak electrolyte partially dissociates, or separates, into its constituent cations and anions as it dissolves, an ion symbol, which indicates the charge of the ion as a superscript on the corresponding elemental symbol, for each of these particles is written on the right side of the "reaction" arrow. Since both cations and anions, which can be monoatomic or polyatomic, are generated during the solvation process, a plus sign, "+", is used to separate their ion symbols.
As stated in Section 7.2, solutions can be prepared using solvents and solutes that exist in the solid, liquid, or gaseous states of matter. If water is utilized to dissolve a solute, the substances that are present in the resultant solution are classified as aqueous, by definition. While these states of matter can be incorporated into a solution equation using the abbreviations "\(\left( s \right)\)," "\(\left( l \right)\)," "\(\left( g \right)\)," and "\(\left( aq \right)\)," respectively, the information that is conveyed by these symbols is not vital to understanding the electrolyte behavior of the solute and, therefore, the states of matter are often omitted from solution equations.
Finally, most solution equations require the incorporation of one or more balancing coefficients, in order to indicate that the Law of Conservation of Matter, which mandates that particles cannot be created or destroyed during a physical or chemical change, is upheld during the solvation process. Recall that a coefficient is a whole-number value that specifies the quantity in which the corresponding particle participates in the transformation that is occurring, and that values of "1" are usually implicitly-understood in chemistry and, therefore, are not written when balancing an equation. As stated above, the solvent does not undergo a physical change during the dissolving process and, consequently, does not exhibit any electrolyte behavior. Therefore, because coefficients are only associated with chemicals that are changing, the chemical formula of the solvent is not considered when balancing a solution equation.

