3.9: Ionic Bonding: Writing Chemical Formulas of Ionic Compounds Containing Transition Metals
- Page ID
- 215705
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Write the chemical formulas of ionic compounds containing transition metal elements.
The previous section of this chapter outlined the complications that arise when transition metal elements ionize. As most transition metals are able to achieve stable electron configurations through multiple ionization pathways, a single transition metal can ionize to form several unique cations. In order to unambiguously distinguish these ions from one another, their corresponding ion names must be modified using either a Roman numeral or a distinctive suffix. However, the suffixes employed in the common system still limit the variety of transition metal cations that can be clearly named. In contrast, the IUPAC system indicates the charge of a transition metal cation by writing a corresponding Roman numeral in parentheses after the element name, but before the word "ion," in an ion name. As the Roman numeral is directly tied to the charge of the cation, the IUPAC system is both less restrictive and less ambiguous than the common system. Therefore, this method for naming transition metal cations will be used exclusively in the remaining sections of this text.
Writing Chemical Formulas of Ionic Compounds Containing Transition Metals
Section 3.6 presented the procedure for determining the chemical formula of an ionic compound containing main group elements. These steps can also be utilized to establish the chemical formula of an ionic compound that contains a transition metal.
For example, consider phosphorus and a tin (IV) ion.
Based on the combinations listed in Section 3.2, these elements will combine to form an ionic compound. Recall that an ionic bond is produced when a cation exists in close physical proximity to an anion, creating an electrostatic attractive force. In the given combination, phosphorus, a non-metal, ionizes to form an anion, and tin (Sn), a metal, ionizes to form a cation. After establishing that a pair of chemicals will form an ionic bond, a five-step process can be employed to determine the chemical formula of the resultant ionic compound.
- Write the ion symbol for the ion that results upon the ionization of each of the given elements. Based on the information presented in the previous sections of this chapter, phosphorus ionizes to form P–3. Tin is able to achieve a stable electron configuration through multiple ionization pathways. For elements that can ionize to form more than one cation, a Roman numeral must be included in the given ion name to specify the charge of the particular cation that is formed. In this example, the Roman numeral (IV) in the given ion name indicates that this ion of tin has a charge of +4 and, therefore, is symbolized as Sn+4.
- In order to ensure consistent formatting in all ionic chemical formulas, the symbol for the cation is written first. In this example, Sn+4 will be written before P–3 in the final chemical formula.
- The signs of the ions are only used to determine the relative order in which the ion symbols are written. As this information was established in the previous step, the "+" and "–" signs can be removed, so that only the base elemental symbols and numerical superscripts remain. In this example, the "+" sign is removed from Sn+4 and the "–" sign is removed from P–3. The revised symbols are written as Sn4 and P3, respectively.
- Use subscripts to indicate how many of each of the given ions are present in the base chemical formula. Two different processes, both of which are presented below, can be used to determine this information.
- The first process, which is considered the more "scientifically-correct" method, is known as the "Ratio Method," as it establishes the correct cation-to-anion ratio by equating the total charges of the cations to the sum of the charges of the anions, in order to ensure that the final compound will be a net-neutral species. To determine this ratio, a mini-equation, in which the larger superscript value is multiplied by 1, and the smaller superscript value is multiplied by a variable, such as x, is solved. In the current example, the larger superscript value is "4," and the smaller superscript value is "3." Therefore,
4(1) = 3(x)
This result indicates that for every 1 of the ions with the larger superscript value, in this case, Sn4, 4⁄3 of the other ions, P3, are required to achieve charge-balance between them. However, subscripts must be written as whole-number values, as it is physically-impossible for a fraction of an ion to exist. Therefore, the third-fraction is cleared by tripling both of the numbers in the ratio indicated above. Therefore, for every 3 of the ions with the larger superscript value, in this case, Sn4, 4 of the other ions, P3, are required to achieve charge-balance between them.
4⁄3 = x (or, x = 1.333...)
To apply this information, remove the numerical superscripts from each symbol and instead utilize subscripts to indicate the ratio established above. Therefore, the resultant chemical formula, which is called a base formula, is Sn3P4.
- The alternative process for establishing this chemical formula is a "shortcut" known as the "Criss-Cross Method." In this system, the superscript on the first symbol becomes the subscript on the second symbol, and the superscript on the second symbol is repositioned as the subscript on the first symbol, as shown below.
This "shortcut" is known as the "Criss-Cross Method" because the numerical values effectively "criss-cross" over one another when they are moved to their new positions. The resultant base formula is identical to what was derived using the first method: Sn3P4.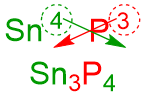
- The first process, which is considered the more "scientifically-correct" method, is known as the "Ratio Method," as it establishes the correct cation-to-anion ratio by equating the total charges of the cations to the sum of the charges of the anions, in order to ensure that the final compound will be a net-neutral species. To determine this ratio, a mini-equation, in which the larger superscript value is multiplied by 1, and the smaller superscript value is multiplied by a variable, such as x, is solved. In the current example, the larger superscript value is "4," and the smaller superscript value is "3." Therefore,
- The final step in this process is to ensure that the subscripts in the base formula are mathematically-appropriate for inclusion in an ionic compound.
- If possible, the subscripts must be reduced to the lowest-common ratio of whole numbers by dividing both of the subscripts by the same numerical value. This division should only be performed if both of the resultant subscripts remain whole numbers. In the current example, no such division is possible. Therefore, the chemical formula remains unchanged: Sn3P4.
- If a "1" has been explicitly-written as a subscript, it must be removed. As indicated previously, values of "1" are usually implicitly-understood in chemistry and, therefore, should not be written in a chemical formula. In this example, no explicitly-written "1"s are present, and the chemical formula again remains unchanged: Sn3P4.
The chemical formula that results upon the completion of this final step is a chemically-correct formula for an ionic compound. Therefore, Sn3P4 is the chemical formula for the compound formed when phosphorus and a tin (IV) ion bond with one another.

