4.1: The Perfect Gas
- Last updated
- Save as PDF
- Page ID
- 204455
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)At the macroscopic level, a complete physical description of a sample of a gas requires four quantities:
- temperature (T, expressed in kelvins),
- volume (V, expressed in liters),
- amount (n, expressed in moles), and
- pressure (P, in atmospheres).
These variables are not independent (i.e., they cannot be arbitrarily be varied). If we know the values of any three of these quantities, we can calculate the fourth and thereby obtain a full physical description of the gas. The volume of a container and the number of gas particles are relatively straightforward concepts, but pressure and temperature will each require some description.
Pressure
Any object, whether it is your computer, a person, or a sample of gas, exerts a force on any surface with which it comes in contact. If the surface exerts exactly that same force against the object, the object and the surface are in mechanical equilibrium. The air in a balloon, for example, exerts a force against the interior surface of the balloon that is equal to the force of the air pushing on the outside of the balloon plus the tensile stress from the balloon wall. If the air in a balloon is heated, the increased kinetic energy of the gas causes the balloon to expand because of the increased pressure (\(P\)) of the gas inside the balloon. This pressure is equal to the force (\(F\)) per unit area (\(A\)) of the balloon surface:
\[P=\dfrac{\rm Force}{\rm Area}=\dfrac{F}{A}\label{1.1.1}\]
Pressure is dependent on both the force exerted and the size of the area to which the force is applied. We know from Equation \(\ref{1.1.1}\) that applying the same force to a smaller area produces a higher pressure. When we use a hose to wash a car, for example, we can increase the pressure of the water by reducing the size of the opening of the hose with a thumb.
The units of pressure are derived from the units used to measure force and area. The SI unit for pressure, derived from the SI units for force (newtons) and area (square meters), is the newton per square meter (\(N/m^2\)), which is called the Pascal (Pa), after the French mathematician Blaise Pascal (1623–1662):
\[\rm 1\; Pa = 1 \; N/m^2\label{1.1.2}\]
Example \(\PageIndex{1}\)
Assuming a paperback book has a mass of 2.00 kg, a length of 27.0 cm, a width of 21.0 cm, and a thickness of 4.5 cm, what pressure, in Pascals, does it exert on a surface if it is
- lying flat?
- standing on edge in a bookcase?
Strategy:
- Calculate the force exerted by the book and then compute the area that is in contact with a surface.
- Substitute these two values into Equation \(\ref{1.1.1}\) to find the pressure exerted on the surface in each orientation.
Solution:
The force exerted by the book does not depend on its orientation. Recall that the force exerted by an object is F = ma, where m is its mass and a is its acceleration. In Earth’s gravitational field, the acceleration is due to gravity (9.8067 m/s2 at Earth’s surface). In SI units, the force exerted by the book is therefore
\[F = ma = 2.00 \;\rm kg\times 9.8067 \dfrac{\rm m}{\rm s^2} = 19.6 \dfrac{\rm kg·m}{\rm s^2} = 19.6\;\rm N\label{1.1.3}\]
A We calculated the force as 19.6 N. When the book is lying flat, the area is
\[A=\rm0.270 \;m\times0.210 \;m= 0.0567 \;m^2.\label{1.1.4}\]
B The pressure exerted by the text lying flat is thus
\[P=\dfrac{F}{A}=\dfrac{19.6\;\rm N}{0.0567\;\rm m^2}=3.46\times10^2 \rm Pa\label{1.1.5}\]
A If the book is standing on its end, the force remains the same, but the area decreases:
\[\rm A=\rm21.0 \;cm\times4.5 \;cm = 0.210 \;m\times0.045 \;m = 9.5 \times 10^{−3} \;\rm m^2\label{1.1.6}\]
B The pressure exerted by the text lying flat is thus
\[P=\dfrac{19.6\;\rm N}{9.5\times10^{-3}\;\rm m^2}=2.06\times10^3 \;\rm Pa\label{1.1.7}\]
Exercise \(\PageIndex{1}\)
What pressure does a 60.0 kg student exert on the floor
- when standing flat-footed in the laboratory in a pair of tennis shoes (the surface area of the soles is approximately 180 cm2)?
- as she steps heel-first onto a dance floor wearing high-heeled shoes (the area of the heel = 1.0 cm2)?
Answers:
- 3.27 × 104 Pa
- 5.9 × 106 Pa
Barometric Pressure
Just as we exert pressure on a surface because of gravity, so does our atmosphere. We live at the bottom of an ocean of gases that becomes progressively less dense with increasing altitude. Approximately 99% of the mass of the atmosphere lies within 30 km of Earth’s surface. Every point on Earth’s surface experiences a net pressure called barometric pressure. The pressure exerted by the atmosphere is considerable: a 1 m2 column, measured from sea level to the top of the atmosphere, has a mass of about 10,000 kg, which gives a pressure of about 101 kPa.
Barometric pressure can be measured using a barometer, a device invented in 1643 by one of Galileo’s students, Evangelista Torricelli (1608–1647). A barometer may be constructed from a long glass tube that is closed at one end. The glass tube is filled with mercury and placed upside down in a dish of mercury without allowing any air to enter the tube. Some of the mercury will run out of the tube, but a relatively tall column remains inside. Why doesn’t all the mercury run out? Gravity is certainly exerting a downward force on the mercury in the tube, but the pull of gravity is opposed by the pressure of the atmosphere pushing down on the surface of the mercury in the dish, which has the net effect of pushing the mercury up into the tube. Because there is no air above the mercury inside the tube in a properly filled barometer (it contains a vacuum), there is no pressure pushing down on the column. Thus the mercury runs out of the tube until the pressure exerted by the mercury column itself exactly balances the pressure of the atmosphere. It can be said that at this point the column of mercury is in mechanical equilibrium with the atmosphere. The pressure exerted by the mercury column can be expressed as:
\[P=\dfrac{F}{A}=\dfrac{mg}{A}=\dfrac{\rho V\cdot g}{A}=\dfrac{ \rho \cdot Ah\cdot g}{A}=\rho gh\; kPa\label{1.1.8}\]
with
- \(g\) is the gravitational acceleration,
- \(m\) is the mass,
- \(\rho\) is the density,
- \(V\) is the volume,
- \(A\) is the bottom area, and
- \(h\) is height of the mercury column.
Mercury barometers have been used to measure barometric pressure for so long that they have their own unit for pressure: the millimeter of mercury (mmHg), often called the torr, after Torricelli. Standard barometric pressure is the barometric pressure required to support a column of mercury exactly 760 mm tall; this pressure is also referred to as 1 atmosphere (atm). These units are also related to the pascal:
\[\rm 1\; atm = 760 \; mmHg = 760 \; torr = 1.01325 \times 10^5 \; Pa = 101.325 \; kPa\label{1.1.9}\]
Exercise \(\PageIndex{2}\)
Suppose you want to design a barometer to measure barometric pressure in an environment that is always hotter than 30°C. To avoid using mercury, you decide to use gallium, which melts at 29.76°C. At 35°C the density of mercury is 13.5 g/cm3 and the density of liquid gallium is 6.11 g/cm3. How tall a column of gallium do you need if P = 1.00 atm?
Answer: 1.69 m
Gas Sample Pressure
Barometers measure barometric pressure, but manometers measure the pressures of samples of gases contained in an apparatus. The key feature of a manometer is a U-shaped tube containing mercury (or occasionally another nonvolatile liquid). A closed-end manometer is shown schematically in part (a) in Figure \(\PageIndex{1}\).
When the bulb contains no gas (i.e., when its interior is a near vacuum), the heights of the two columns of mercury are the same because the space above the mercury on the left is a near vacuum (it contains only traces of mercury vapor). If a gas is released into the bulb on the right, it will exert a pressure on the mercury in the right column, and the two columns of mercury will no longer be the same height. The difference between the heights of the two columns is equal to the pressure of the gas.
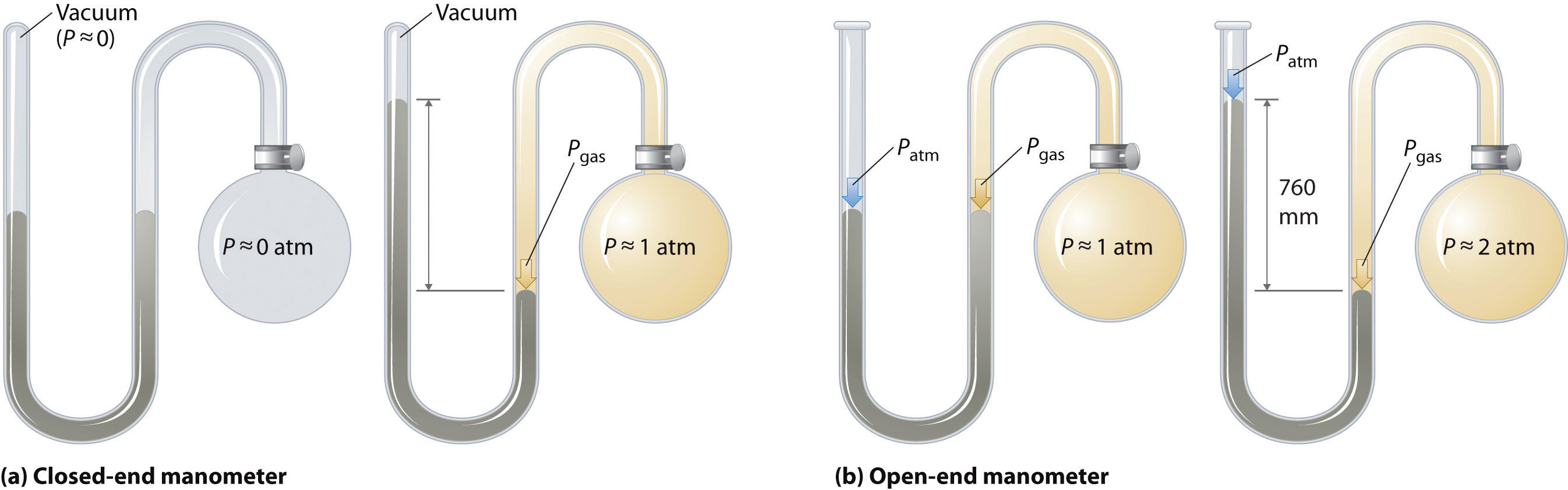
Figure \(\PageIndex{1}\): The Two Types of Manometer. (a) In a closed-end manometer, the space above the mercury column on the left (the reference arm) is essentially a vacuum (P ≈ 0), and the difference in the heights of the two columns gives the pressure of the gas contained in the bulb directly. (b) In an open-end manometer, the left (reference) arm is open to the atmosphere (P ≈ 1 atm), and the difference in the heights of the two columns gives the difference between barometric pressure and the pressure of the gas in the bulb.
If the tube is open to the atmosphere instead of closed, as in the open-end manometer shown in part (b) in Figure \(\PageIndex{1}\) , then the two columns of mercury have the same height only if the gas in the bulb has a pressure equal to the barometric pressure. If the gas in the bulb has a higher pressure, the mercury in the open tube will be forced up by the gas pushing down on the mercury in the other arm of the U-shaped tube. The pressure of the gas in the bulb is therefore the sum of the barometric pressure (measured with a barometer) and the difference in the heights of the two columns. If the gas in the bulb has a pressure less than that of the atmosphere, then the height of the mercury will be greater in the arm attached to the bulb. In this case, the pressure of the gas in the bulb is the barometric pressure minus the difference in the heights of the two columns.
Barometers and manometers are hydrostatic pressure gauges, involving the use of a column of liquid. Mechanical gauges that do not use liquids generally contain some surface (tube, diaphragm, wire, or semiconductor) that changes shape in response to a pressure change. There are also pressure gauges that respond to an extrinsic property of the gas sample, such as thermal conductivity or the extent of ionization.
Temperature
Many people confuse temperature with heat. Temperature is a measure of how hot or cold an object is relative to another object (its thermal energy content), whereas heat is the flow of thermal energy between objects with different temperatures.
Three different scales are commonly used to measure temperature: Fahrenheit (expressed as °F), Celsius (°C), and Kelvin (K). Thermometers measure temperature by using materials that expand or contract when heated or cooled. Mercury or alcohol thermometers, for example, have a reservoir of liquid that expands when heated and contracts when cooled, so the liquid column lengthens or shortens as the temperature of the liquid changes.
The Fahrenheit Scale
The Fahrenheit temperature scale was developed in 1717 by the German physicist Gabriel Fahrenheit, who designated the temperature of a bath of ice melting in a solution of salt as the zero point on his scale. Such a solution was commonly used in the 18th century to carry out low-temperature reactions in the laboratory. The scale was measured in increments of 12; its upper end, designated as 96°, was based on the armpit temperature of a healthy person—in this case, Fahrenheit’s wife. Later, the number of increments shown on a thermometer increased as measurements became more precise. The upper point is based on the boiling point of water, designated as 212° to maintain the original magnitude of a Fahrenheit degree, whereas the melting point of ice is designated as 32°.
The Celsius Scale
The Celsius scale was developed in 1742 by the Swedish astronomer Anders Celsius. It is based on the melting and boiling points of water under normal atmospheric conditions. The current scale is an inverted form of the original scale, which was divided into 100 increments. Because of these 100 divisions, the Celsius scale is also called the centigrade scale.
The Kelvin Scale
Lord Kelvin, working in Scotland, developed the Kelvin scale in 1848. His scale uses molecular energy to define the extremes of hot and cold. Absolute zero, or 0 K, corresponds to the point at which molecular energy is at a minimum. Absolute zero is the lowest temperature possible. The Kelvin scale is preferred in scientific work, although the Celsius scale is also commonly used. Temperatures measured on the Kelvin scale are reported simply as K, not °K.
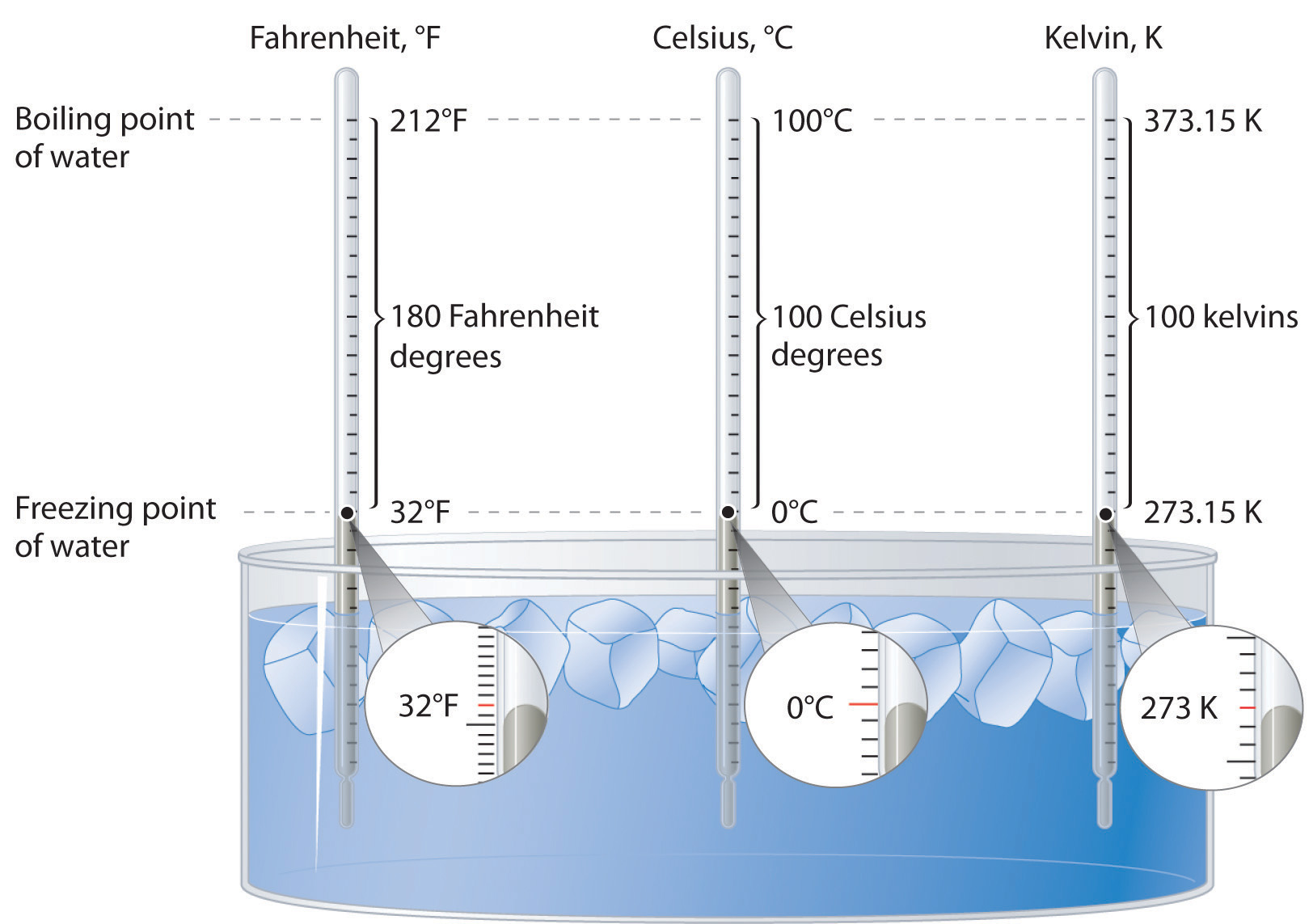
Figure \(\PageIndex{2}\): A Comparison of the Fahrenheit, Celsius, and Kelvin Temperature Scales. Because the difference between the freezing point of water and the boiling point of water is 100° on both the Celsius and Kelvin scales, the size of a degree Celsius (°C) and a kelvin (K) are precisely the same. In contrast, both a degree Celsius and a kelvin are 9/5 the size of a degree Fahrenheit (°F).
Converting between Scales
The kelvin is the same size as the Celsius degree, so measurements are easily converted from one to the other. The freezing point of water is 0°C = 273.15 K; the boiling point of water is 100°C = 373.15 K. The Kelvin and Celsius scales are related as follows:
T (in °C) + 273.15 = T (in K)
T (in K) − 273.15 = T (in °C)
Degrees on the Fahrenheit scale, however, are based on an English tradition of using 12 divisions, just as 1 ft = 12 in. The relationship between degrees Fahrenheit and degrees Celsius is as follows:where the coefficient for degrees Fahrenheit is exact. (Some calculators have a function that allows you to convert directly between °F and °C.) There is only one temperature for which the numerical value is the same on both the Fahrenheit and Celsius scales: −40°C = −40°F. The relationship between the scales are as follows:
°C = (5/9)*(°F-32)
°F = (9/5)*(°C)+32
The Equation of State for Perfect Gases
An equation of state is an equation that relates the variables which are required to fully describe a state of matter. One example of an equation of state is V = f(p,T, n), which states that volume of a sample of matter is a function of the pressure, temperature, and the number of particles in this sample. The exact expression for this relationship, the perfect gas law, will now be derived. (A gas sample in which there are no interactions among the particles is a perfect gas. A gas sample in which all of the interactions are identical is an ideal gas. Thus, all perfect gases are ideal gases, but not all ideal gases are perfect gases.)
Deriving the Perfect Gas Law
The relationship between a single quantity (such as V) and all of the other variables (\(p\), \(T\), and \(n\)) was obtained by combining the following three expressions into a single equation that describes all the relationships simultaneously:
- Boyle’s law
\[V \propto \dfrac{1}{P} \;\; \text{@ constant n and T}\label{1.1.10}\]
- Charles’s law
\[V \propto T \;\; \text{@ constant n and P}\label{1.1.11}\]
- Avogadro’s principle
\[V \propto n \;\; \text{@ constant T and P}\label{1.1.12}\]
Combining these three expressions gives
\[V \propto \dfrac{nT}{P}\label{1.1.13}\]
which shows that the volume of a gas is proportional to the number of moles and the temperature and inversely proportional to the pressure. This expression can also be written as
\[V= {\rm Cons.} \left( \dfrac{nT}{P} \right)\label{1.1.14} \]
By convention, the proportionality constant in Equation \(\ref{1.1.14}\) is called the gas constant, which is represented by the letter \(R\). Inserting R into Equation \(\ref{1.1.14}\) gives
\[ V = \dfrac{nRT}{P} \label{1.1.15} \]
Clearing the fractions by multiplying both sides of Equation \(\ref{1.1.15}\) by \(P\) gives
\[PV = nRT \label{1.1.16}\]
The value of \(R\) can be found by multiplying Boltzmann's constant \((N_A)\) by Avogadro's constant \((k)\),
\[R = N_Ak\label{1.1.17}\]
Values of \(R\) in several common units are shown in the following table:
| Value of \(R\) | Units |
| 8.3145 | \(\dfrac{J}{K·mole}\) |
| 0.082057 | \(\dfrac{dm^3·atm}{K·mole}\) |
| 0.083145 | \(\dfrac{dm^3·bar}{K·mole}\) |
| 8.3145 | \(\dfrac{m^3·Pa}{K·mole}\) |
| 1.9872 | \(\dfrac{cal}{K·mole}\) |
The Relationship between Pressure and Volume: Boyle's Law
As the pressure on a gas increases, the volume of the gas decreases because the gas particles are forced closer together. Conversely, as the pressure on a gas decreases, the gas volume increases because the gas particles can now move farther apart. Weather balloons get larger as they rise through the atmosphere to regions of lower pressure because the volume of the gas has increased; that is, the atmospheric gas exerts less pressure on the surface of the balloon, so the interior gas expands until the internal and external pressures are equal.
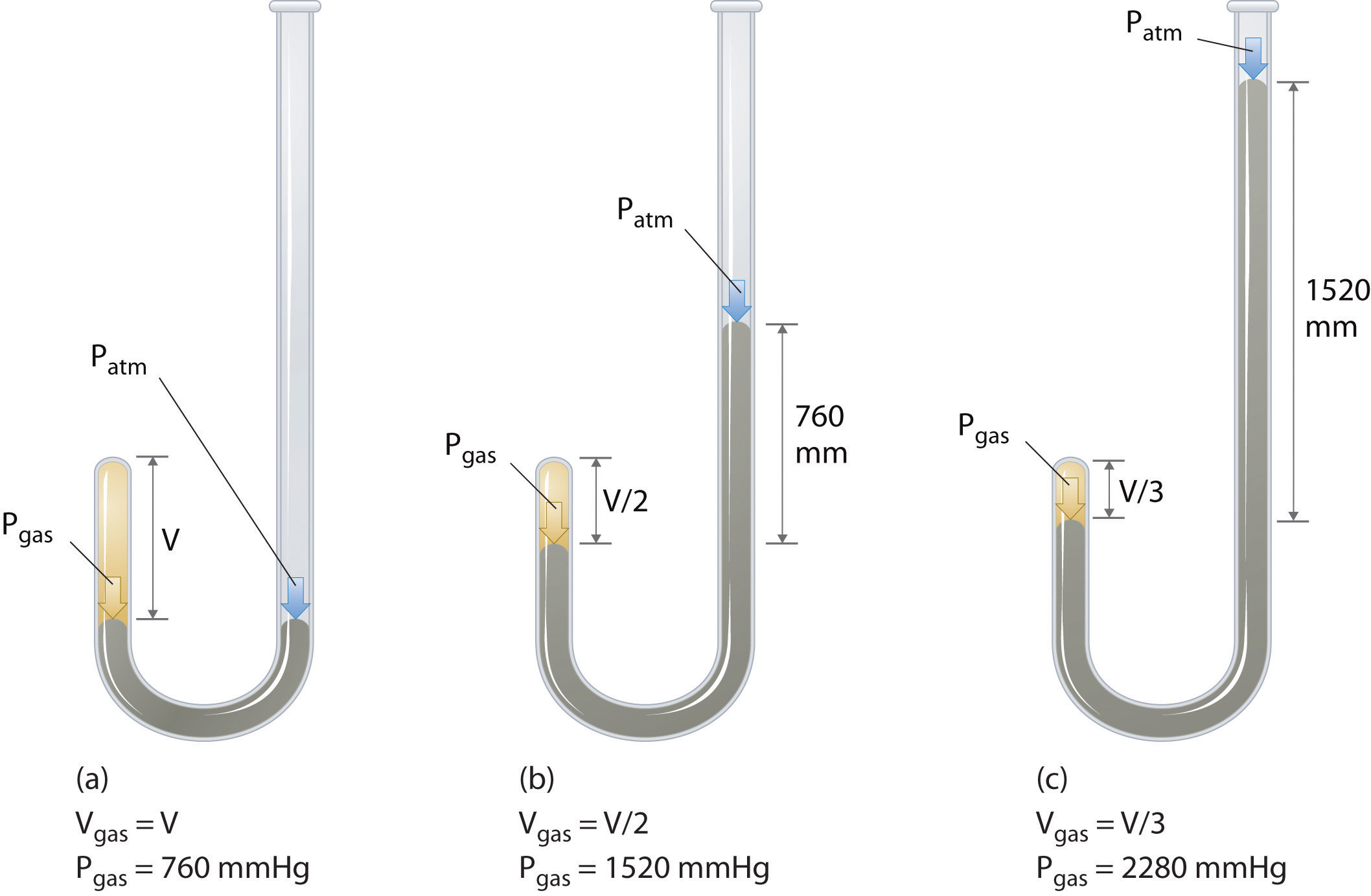
Figure \(\PageIndex{3}\): Boyle’s Experiment Using a J-Shaped Tube to Determine the Relationship between Gas Pressure and Volume. (a) Initially the gas is at a pressure of 1 atm = 760 mmHg (the mercury is at the same height in both the arm containing the sample and the arm open to the atmosphere); its volume is V. (b) If enough mercury is added to the right side to give a difference in height of 760 mmHg between the two arms, the pressure of the gas is 760 mmHg (atmospheric pressure) + 760 mmHg = 1520 mmHg and the volume is V/2. (c) If an additional 760 mmHg is added to the column on the right, the total pressure on the gas increases to 2280 mmHg, and the volume of the gas decreases to V/3.
The Irish chemist Robert Boyle (1627–1691) carried out some of the earliest experiments that determined the quantitative relationship between the pressure and the volume of a gas. Boyle used a J-shaped tube partially filled with mercury, as shown in Figure \(\PageIndex{3}\). In these experiments, a small amount of a gas or air is trapped above the mercury column, and its volume is measured at atmospheric pressure and constant temperature. More mercury is then poured into the open arm to increase the pressure on the gas sample. The pressure on the gas is atmospheric pressure plus the difference in the heights of the mercury columns, and the resulting volume is measured. This process is repeated until either there is no more room in the open arm or the volume of the gas is too small to be measured accurately. Data such as those from one of Boyle’s own experiments may be plotted in several ways Figure \(\PageIndex{4}\). A simple plot of \(V\) versus \(P\) gives a curve called a hyperbola and reveals an inverse relationship between pressure and volume: as the pressure is doubled, the volume decreases by a factor of two. This relationship between the two quantities is described as follows:
\[PV = \rm constant \label{1.1.18}\]
Dividing both sides by \(p\) gives an equation illustrating the inverse relationship between \(P\) and \(V\):
\[V=\dfrac{\rm const.}{P}= const.\left(\dfrac{1}{P}\right)\label{1.1.19}\]
or
\[V \propto \dfrac{1}{P}\label{1.1.20} \]
where the ∝ symbol is read “is proportional to.” A plot of V versus 1/P is thus a straight line whose slope is equal to the constant in Equations \(\ref{1.1.18}\) and \(\ref{1.1.19}\). Dividing both sides of Equation \(\ref{1.1.18}\) by V instead of P gives a similar relationship between P and 1/V. The numerical value of the constant depends on the amount of gas used in the experiment and on the temperature at which the experiments are carried out. This relationship between pressure and volume is known as Boyle's Law, after its discoverer, and can be stated as follows: At constant temperature, the volume of a fixed amount of a gas is inversely proportional to its pressure. This law in practice is shown in Figure \(\PageIndex{4}\).
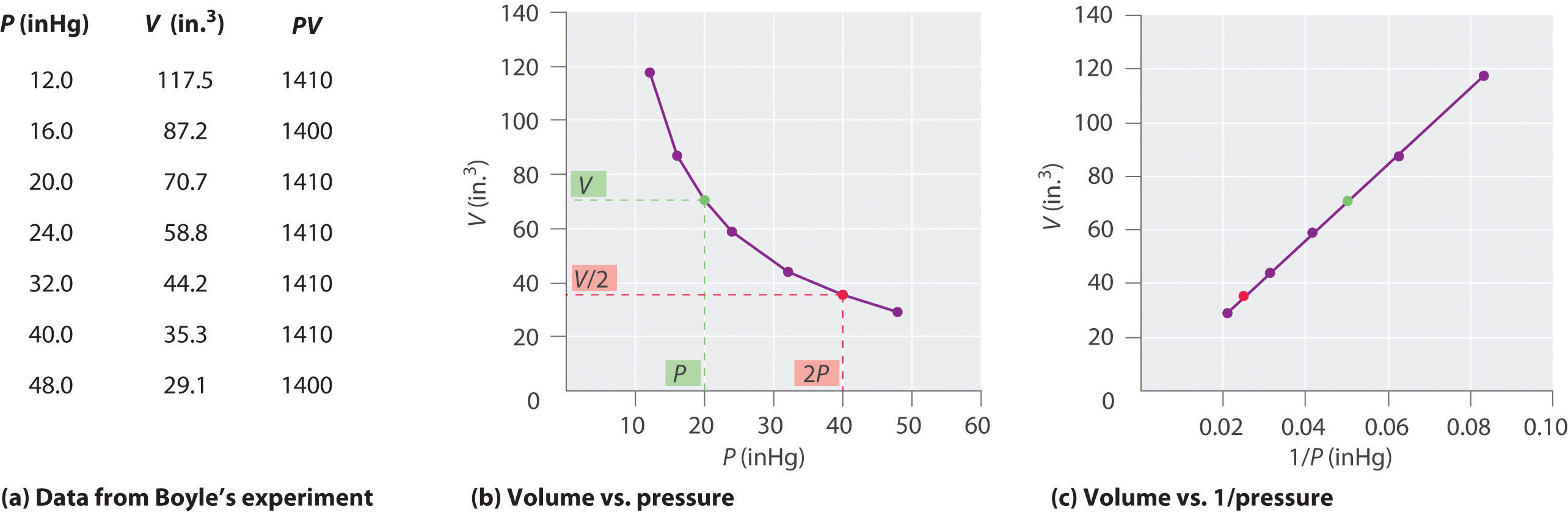
Figure \(\PageIndex{4}\): Plots of Boyle’s Data. (a) Here are actual data from a typical experiment conducted by Boyle. Boyle used non-SI units to measure the volume (in.3 rather than cm3) and the pressure (in. Hg rather than mmHg). (b) This plot of pressure versus volume at constant temperature (known as an isotherm) is a hyperbola. Because PV is a constant, decreasing the pressure by a factor of two results in a twofold increase in volume and vice versa. (c) An isotherm of volume versus 1/pressure for the same data shows the inverse linear relationship between the two quantities, as expressed by the equation V = constant/P.
The Relationship between Temperature and Volume: Charles's Law
The first experiments to quantify the relationship between the temperature and the volume of a gas were carried out in 1783 by an avid balloonist, the French chemist Jacques Alexandre César Charles (1746–1823). Charles’s initial experiments showed that a plot of the volume of a given sample of gas versus temperature (in degrees Celsius) at constant pressure is a straight line. Similar but more precise studies were carried out by another balloon enthusiast, the Frenchman Joseph-Louis Gay-Lussac (1778–1850), who showed that a plot of V versus T was a straight line that could be extrapolated to a point at zero volume, a theoretical condition now known to correspond to −273.15°C (Figure \(\PageIndex{5}\)).A sample of gas cannot really have a volume of zero because any sample of matter must have some volume. Furthermore, at 1 atm pressure all gases liquefy at temperatures well above −273.15°C. Note from part (a) in Figure \(\PageIndex{5}\) that the slope of the plot of V versus T varies for the same gas at different pressures but that the intercept remains constant at −273.15°C. Similarly, as shown in part (b) in Figure \(\PageIndex{5}\), plots of V versus T for different amounts of varied gases are straight lines with different slopes but the same intercept on the T axis.
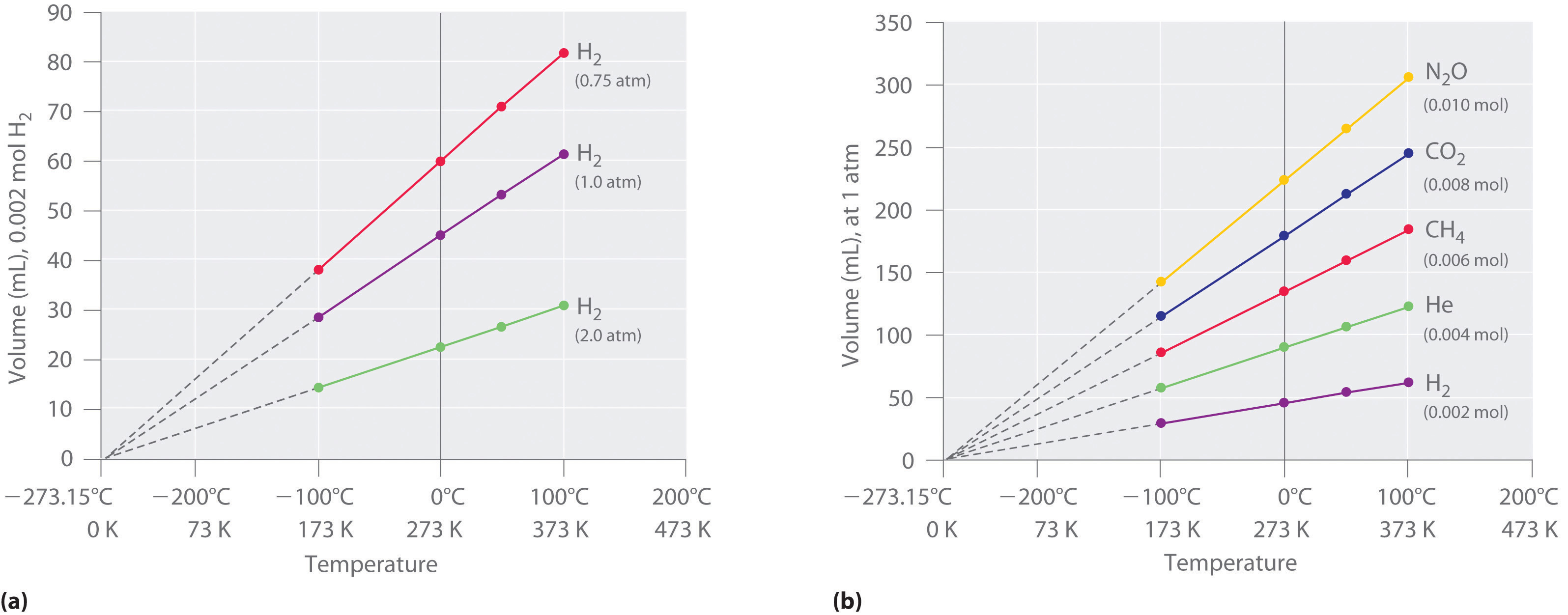
Figure \(\PageIndex{5}\): The Relationship between Volume and Temperature at Constant Pressure. (a) In these plots of volume versus temperature at constant pressure (called isobars) for equal-sized samples of H2 at three different pressures, the solid lines show the experimentally measured data down to −100°C, and the broken lines show the extrapolation of the data to V = 0. The temperature scale is given in both degrees Celsius and kelvins. Although the slopes of the lines decrease with increasing pressure, all of the lines extrapolate to the same temperature at V = 0 (−273.15°C = 0 K). (b) In these isobars for different amounts of selected gases at 1 atm pressure, all the plots extrapolate to a value of V = 0 at −273.15°C, regardless of the identity or the amount of the gas.
The significance of the invariant T intercept in plots of V versus T was recognized in 1848 by the British physicist William Thomson (1824–1907), later named Lord Kelvin. He postulated that −273.15°C was the lowest possible temperature that could theoretically be achieved, for which he coined the term absolute zero (0 K).
We can state Charles’s and Gay-Lussac’s findings in simple terms: At constant pressure, the volume of a fixed amount of gas is directly proportional to its absolute temperature (in kelvins). This relationship, illustrated in part (b) in Figure \(\PageIndex{5}\) is often referred to as Charles’s law and is stated mathematically as
\[V ={\rm const.}\; T \label{1.1.21}\]
or
\[V \propto T\label{1.1.22} \]
with temperature expressed in kelvins, not in degrees Celsius. Charles’s law is valid for virtually all gases at temperatures well above their boiling points.
The Relationship between Amount and Volume: Avogadro's Law
We can demonstrate the relationship between the volume and the amount of a gas by filling a balloon; as we add more gas, the balloon gets larger. The specific quantitative relationship was discovered by the Italian chemist Amedeo Avogadro, who recognized the importance of Gay-Lussac’s work on combining volumes of gases. In 1811, Avogadro postulated that, at the same temperature and pressure, equal volumes of gases contain the same number of gaseous particles (Figure \(\PageIndex{6}\)). This is the historic “Avogadro’s hypothesis.”
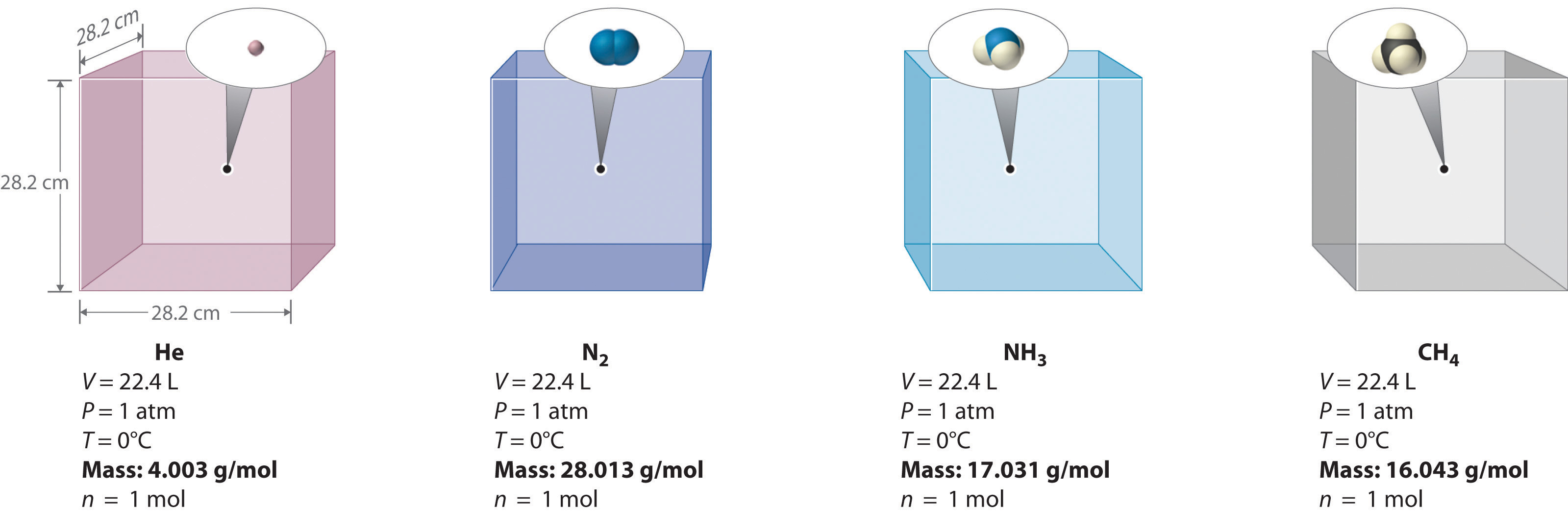
Figure \(\PageIndex{6}\): Avogadro’s Hypothesis. Equal volumes of four different gases at the same temperature and pressure contain the same number of gaseous particles. Because the molar mass of each gas is different, the mass of each gas sample is different even though all contain 1 mol of gas.
A logical corollary to Avogadro's hypothesis (sometimes called Avogadro's law) describes the relationship between the volume and the amount of a gas: At constant temperature and pressure, the volume of a sample of gas is directly proportional to the number of moles of gas in the sample. Stated mathematically,
\[V ={\rm const.}\; n \label{1.1.23} \]
or
\[V \propto n\label{1.1.24} \]
This relationship is valid for most gases at relatively low pressures, but deviations from strict linearity are observed at elevated pressures.
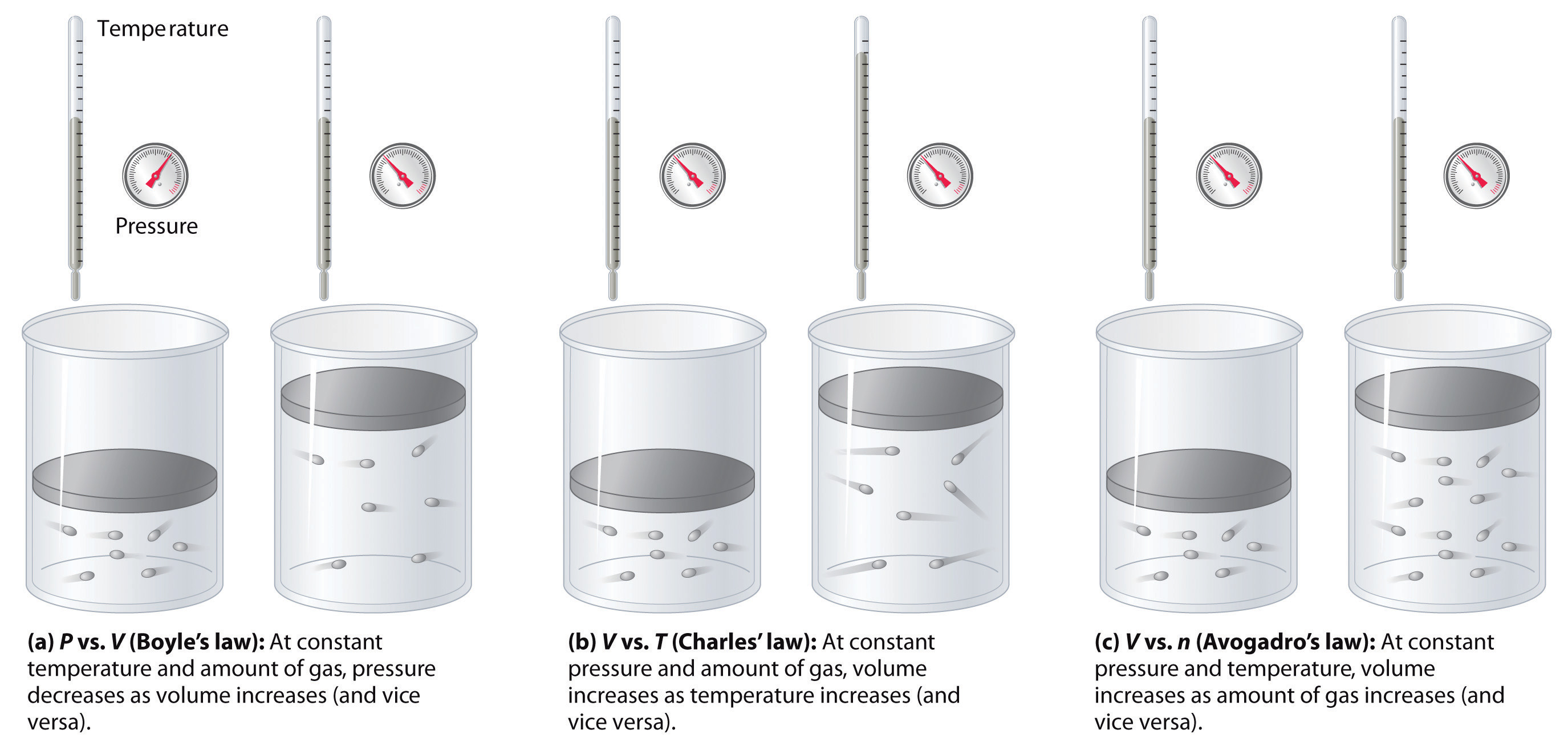
Figure \(\PageIndex{7}\): The Empirically Determined Relationships among Pressure, Volume, Temperature, and Amount of a Gas. The thermometer and pressure gauge indicate the temperature and the pressure qualitatively, the level in the flask indicates the volume, and the number of particles in each flask indicates relative amounts.
A perfect gas is defined as a hypothetical gaseous substance whose behavior is independent of attractive and repulsive forces and can be completely described by the perfect gas law. In reality, there is no such thing as an perfect gas, but an perfect gas is a useful conceptual model that allows us to understand how gases respond to changing conditions. As we shall see, under many conditions, most real gases exhibit behavior that closely approximates that of a perfect gas. The perfect gas law can therefore be used to predict the behavior of real gases under most conditions. The perfect gas law does not work well at very low temperatures or very high pressures, where deviations from perfect behavior are most commonly observed.
Applying the Perfect Gas Law
The perfect gas law allows us to calculate the value of the fourth variable for a gaseous sample if we know the values of any three of the four variables (P, V, T, and n). It also allows us to predict the final state of a sample of a gas (i.e., its final temperature, pressure, volume, and amount) following any changes in conditions if the parameters (P, V, T, and n) are specified for an initial state. Some applications are illustrated in the following examples. The approach used throughout is always to start with the same equation—the perfect gas law—and then determine which quantities are given and which need to be calculated. Let’s begin with simple cases in which we are given three of the four parameters needed for a complete physical description of a gaseous sample.
Example \(\PageIndex{2}\)
The balloon that Charles used for his initial flight in 1783 was destroyed, but we can estimate that its volume was 31,150 L (1100 ft3), given the dimensions recorded at the time. If the temperature at ground level was 86°F (30°C) and the atmospheric pressure was 745 mmHg, how many moles of hydrogen gas were needed to fill the balloon?
Strategy:
- Solve the perfect gas law for the unknown quantity, in this case n.
- Make sure that all quantities are given in units that are compatible with the units of the gas constant. If necessary, convert them to the appropriate units, insert them into the equation you have derived, and then calculate the number of moles of hydrogen gas needed.
Solution:
A We are given values for P, T, and V and asked to calculate n. If we solve the ideal gas law (Equation \(\ref{1.1.16}\)) for n, we obtain
\[n=\dfrac{PV}{RT} \label{1.1.25} \]
B P and T are given in units that are not compatible with the units of the gas constant [R = 0.08206 (L•atm)/(K•mol)]. We must therefore convert the temperature to kelvins and the pressure to atmospheres:
\[T=273+30=303{\rm K}\label{1.1.26}\]
\[\rm745\;mmHg\times\dfrac{1\;atm}{760\;mmHg}=0.980\;atm\label{1.1.27}\]
Substituting these values into the expression we derived for n, we obtain
\[n=\dfrac{PV}{RT}=\rm\dfrac{0.980\;atm\times31150\;L}{0.08206\dfrac{atm\cdot L}{\rm mol\cdot K}\times 303\;K}=1.23\times10^3\;mol\label{1.1.28}\]
Exercise \(\PageIndex{3}\)
Suppose that an “empty” aerosol spray-paint can has a volume of 0.406 L and contains 0.025 mol of a propellant gas such as CO2. What is the pressure of the gas at 25°C?
Answer: 1.5 atm
General Gas Equation
When one sample of gas is described under two different conditions, the ideal gas equation must be applied twice - to an initial condition and a final condition. This is:
\[\begin{array}{cc}\text{Initial condition }(i) & \text{Final condition} (f)\\P_iV_i=n_iRT_i & P_fV_f=n_fRT_f\end{array}\label{1.1.29}\]
Both equations can be rearranged to give:
\[R=\dfrac{P_iV_i}{n_iT_i} \hspace{1cm} R=\dfrac{P_fV_f}{n_fT_f}\label{1.1.30}\]
The two equations are equal to each other since each is equal to the same constant \(R\). Therefore, we have:
\[\dfrac{P_iV_i}{n_iT_i}=\dfrac{P_fV_f}{n_fT_f}\label{1.1.31}\]
The equation is called the general gas equation, or the combined gas law. The equation is particularly useful when one or two of the gas properties are held constant between the two conditions. In such cases, the equation can be simplified by eliminating these constant gas properties.
Example \(\PageIndex{3}\)
Suppose that Charles had changed his plans and carried out his initial flight not in August but on a cold day in January, when the temperature at ground level was −10°C (14°F). How large a balloon would he have needed to contain the same amount of hydrogen gas at the same pressure as in Example \(\PageIndex{2}\)?
Strategy:
- Use the results from Example \(\PageIndex{2}\) for August as the initial conditions and then calculate the change in volume due to the change in temperature from 30°C to −10°C. Begin by constructing a table showing the initial and final conditions.
- Simplify the general gas equation by eliminating the quantities that are held constant between the initial and final conditions, in this case \(P\) and \(n\).
- Solve for the unknown parameter.
Solution:
A To see exactly which parameters have changed and which are constant, prepare a table of the initial and final conditions:
| Initial (August) | Final (January) |
|---|---|
| \(T_i=30\)°C = 303 K | \(T_f=\)−10°C = 263 K |
| \(P_i=\)0.980 atm | \(P_f=\)0.980 atm |
| \(n_i=\)1.23 × 103 mol | \(n_f=\)1.23 × 103 mol |
| \(V_i=31150\) L | \(V_f=?\) |
B Both \(n\) and \(P\) are the same in both cases (\(n_i=n_f,P_i=P_f\)). Therefore, Equation can be simplified to:
\[\dfrac{V_i}{T_i}=\dfrac{V_f}{T_f}\label{1.1.32}\]
This is the relationship first noted by Charles.
C Solving the equation for \(V_f\), we get:
\[V_f=V_i\times\dfrac{T_f}{T_i}=\rm31150\;L\times\dfrac{263\;K}{303\;K}=2.70\times10^4\;L\label{1.1.33}\]
It is important to check your answer to be sure that it makes sense, just in case you have accidentally inverted a quantity or multiplied rather than divided. In this case, the temperature of the gas decreases. Because we know that gas volume decreases with decreasing temperature, the final volume must be less than the initial volume, so the answer makes sense. We could have calculated the new volume by plugging all the given numbers into the perfect gas law, but it is generally much easier and faster to focus on only the quantities that change.
Exercise \(\PageIndex{4}\)
Suppose that a fire extinguisher, filled with CO2 to a pressure of 20.0 atm at 21°C at the factory, is accidentally left in the sun in a closed automobile in Tucson, Arizona, in July. The interior temperature of the car rises to 160°F (71.1°C). What is the internal pressure in the fire extinguisher?
Answer: 23.4 atm
In Example \(\PageIndex{3}\) , two of the four parameters (P, V, T, and n) were fixed while one was allowed to vary, and we were interested in the effect on the value of the fourth. In fact, we often encounter cases where two of the variables P, V, and T are allowed to vary for a given sample of gas (hence n is constant), and we are interested in the change in the value of the third under the new conditions.
Standard Conditions for Comparing Gas Samples
Scientists have chosen several sets of conditions to use as references:
Standard Ambient Temperature and Pressure (SATP) 25.0°C (298.15 K) and \(\rm1\; bar = 100 \;kPa = 10^5\;Pa\) pressure,
\[\text{SATP:} \hspace{2cm} T=298.15\;{\rm K}\text{ and }P=\rm 1\;bar=10^5\;Pa\label{1.1.34}\]
Standard Temperature and Pressure (STP) 0.0°C (273.15 K) and 1 atm pressure,
\[\text{STP:} \hspace{2cm} T=273.15\;{\rm K}\text{ and }P=\rm 1\;atm\label{1.1.35}\]
We can calculate the volume of 1.000 mol of an ideal gas under standard conditions using the variant of the perfect gas law given in Equation \(\ref{1.1.15}\):
\[V=\dfrac{nRT}{P}\tag{1.1.15}\]
Thus the volume of 1 mol of an ideal gas is 24.79 L at SATP and 22.41 L at STP, approximately equivalent to the volume of three basketballs. The molar volumes of several real gases at 0°C and 1 atm are given in Table 1A.2, which shows that the deviations from ideal gas behavior are quite small. Thus the ideal gas law does a good job of approximating the behavior of real gases at 0°C and 1 atm.
| Gas | Molar Volume (L) |
|---|---|
| NH3 | 22.079 |
| CO2 | 22.260 |
| Ar | 22.397 |
| O2 | 22.397 |
| N2 | 22.402 |
| H2 | 22.433 |
| He | 22.434 |
P, V, T Surfaces
The ideal gas law is derived from empirical relationships among the pressure, the volume, the temperature, and the number of moles of a gas; it can be used to calculate any of the four properties if the other three are known. All of the empirical gas relationships are special cases of the ideal gas law in which two of the four parameters are held constant. The ideal gas law allows us to calculate the value of the fourth quantity (P, V, T, or n) needed to describe a gaseous sample when the others are known and also predict the value of these quantities following a change in conditions if the original conditions (values of P, V, T, and n) are known. The blue surface in the figure below shows some of the possible P, V, and T combinations for a fixed sample of a perfect gas. This sample of perfect gas can only exist in states that correspond to specific points on the surface shown.
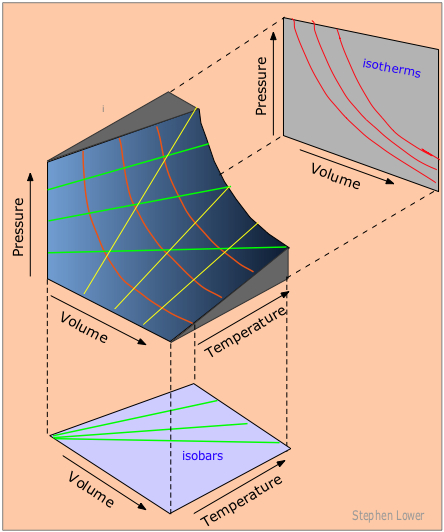
Figure \(\PageIndex{8}\): A P,V,T Surface of a Fixed Sample of Perfect Gas. The central figure shows possible P, V, and T combinations for a fixed sample of a perfect gas. The graph below shows three possible isobars (constant pressure). The graph on the upper right shows three possible isotherms (constant temperature). The yellow lines on the P, V, T surface represent isochores, plots of pressure versus temperature at constant volume.
http://www.chem1.com/acad/webtext/gas/gas_2.html#4A ( Creative Commons Attribution-Share Alike 3.0 License )
Mixtures of Perfect Gases
The perfect gas law assumes that all gases behave identically and that their behavior is independent of attractive and repulsive forces. If volume and temperature are held constant, the perfect gas equation can be rearranged to show that the pressure of a sample of gas is directly proportional to the number of moles of gas present:
\[P=n \left(\dfrac{RT}{V}\right) = n \times \rm const. \label{1.1.36}\]
Nothing in the equation depends on the nature of the gas—only the amount.
With this assumption, let’s suppose we have a mixture of two perfect gases that are present in equal amounts. What is the total pressure of the mixture? Because the pressure depends on only the total number of particles of gas present, the total pressure of the mixture will simply be twice the pressure of either component. More generally, the total pressure exerted by a mixture of gases at a given temperature and volume is the sum of the pressures exerted by each gas alone. Furthermore, if we know the volume, the temperature, and the number of moles of each gas in a mixture, then we can calculate the pressure exerted by each gas individually, which is its partial pressure, the pressure the gas would exert if it were the only one present (at the same temperature and volume).
To summarize, the total pressure exerted by a mixture of gases is the sum of the partial pressures of component gases. This law was first discovered by John Dalton, the father of the atomic theory of matter. It is now known as Dalton’s law of partial pressures. We can write it mathematically as
\[P_{tot}= P_1+P_2+P_3+P_4 \; ... = \sum_{i=1}^n{P_i}\label{1.1.37}\]
where \(P_{tot}\) is the total pressure and the other terms are the partial pressures of the individual gases (up to \(n\) component gases).
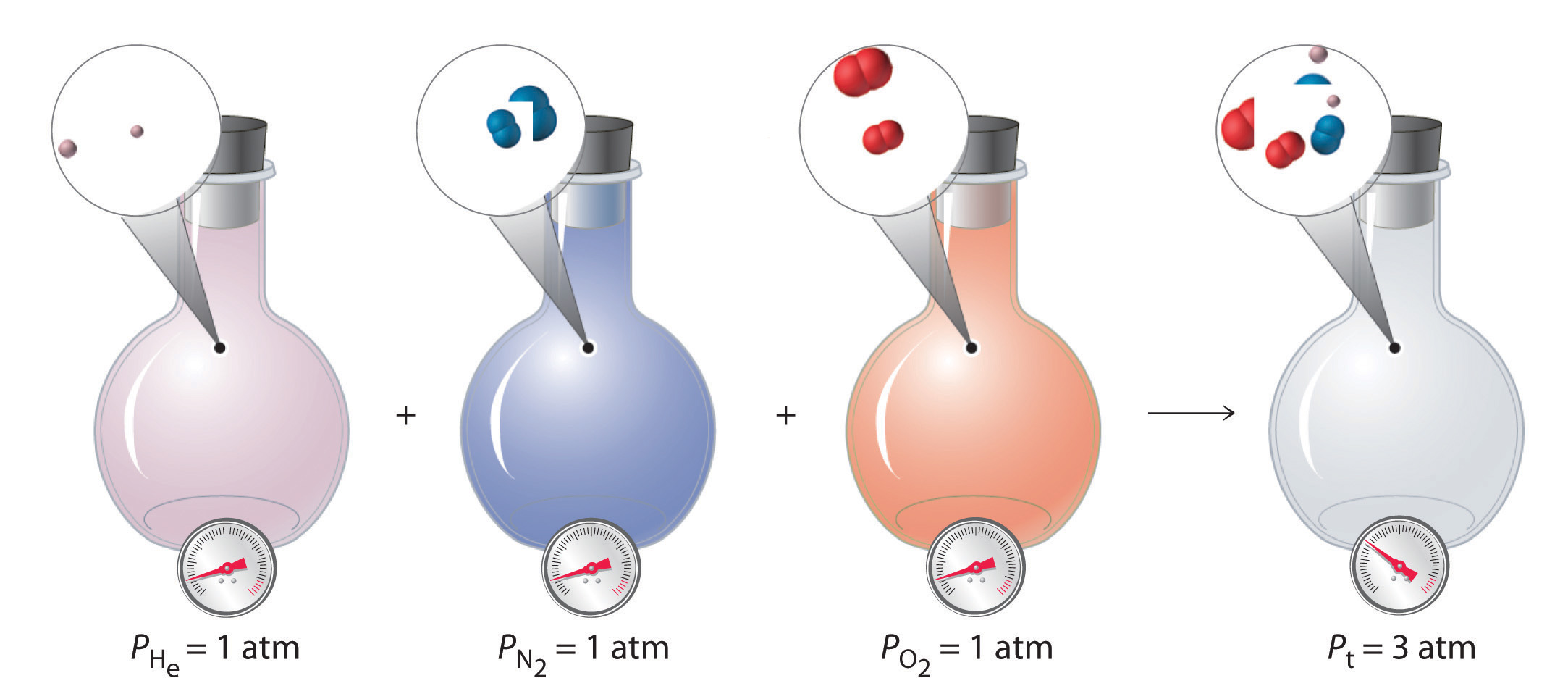
Figure \(\PageIndex{9}\): Dalton’s Law. The total pressure of a mixture of gases is the sum of the partial pressures of the individual gases.
For a mixture of two perfect gases, \(A\) and \(B\), we can write an expression for the total pressure:
\[P_{tot}=P_A+P_B=n_A\bigg(\dfrac{RT}{V}\bigg) + n_B\bigg(\dfrac{RT}{V}\bigg)=(n_A+n_B)\bigg(\dfrac{RT}{V}\bigg)\label{1.1.38}\]
More generally, for a mixture of \(n\) component gases, the total pressure is given by
\[P_{tot}=(P_1+P_2+P_3+ \; \cdots +P_n)\bigg(\dfrac{RT}{V}\bigg)\label{1.1.39}\]
\[P_{tot}=\sum_{i=1}^n{n_i}\bigg(\dfrac{RT}{V}\bigg)\label{1.1.40}\]
Equation \(\ref{1.1.40}\) restates Equation \(\ref{1.1.37}\) in a more general form and makes it explicitly clear that, at constant temperature and volume, the pressure exerted by a gas depends on only the total number of moles of gas present, whether the gas is a single chemical species or a mixture of dozens or even hundreds of gaseous species. For Equation \(\ref{1.1.40}\) to be valid, the identity of the particles present cannot have an effect. Thus a perfect gas must be one whose properties are not affected by either the size of the particles or their intermolecular interactions because both will vary from one gas to another. The calculation of total and partial pressures for mixtures of gases is illustrated in Example \(\PageIndex{4}\).
Example \(\PageIndex{4}\): The Bends
Deep-sea divers must use special gas mixtures in their tanks, rather than compressed air, to avoid serious problems, most notably a condition called “the bends.” At depths of about 350 ft, divers are subject to a pressure of approximately 10 atm. A typical gas cylinder used for such depths contains 51.2 g of \(O_2\) and 326.4 g of He and has a volume of 10.0 L. What is the partial pressure of each gas at 20.00°C, and what is the total pressure in the cylinder at this temperature?
Strategy:
- Calculate the number of moles of \(He\) and \(O_2\) present.
- Use the perfect gas law to calculate the partial pressure of each gas. Then add together the partial pressures to obtain the total pressure of the gaseous mixture.
Solution:
A The number of moles of \(He\) is
\[n_{\rm He}=\rm\dfrac{326.4\;g}{4.003\;g/mol}=81.54\;mol\label{1.1.41}\]
The number of moles of \(O_2\) is
\[n_{\rm O_2}=\rm \dfrac{51.2\;g}{32.00\;g/mol}=1.60\;mol\label{1.1.42}\]
B We can now use the perfect gas law to calculate the partial pressure of each:
\[P_{\rm He}=\dfrac{n_{\rm He}RT}{V}=\rm\dfrac{81.54\;mol\times0.08206\;\dfrac{atm\cdot L}{mol\cdot K}\times293.15\;K}{10.0\;L}=196.2\;atm\label{1.1.43}\]
\[P_{\rm O_2}=\dfrac{n_{\rm O_2} RT}{V}=\rm\dfrac{1.60\;mol\times0.08206\;\dfrac{atm\cdot L}{mol\cdot K}\times293.15\;K}{10.0\;L}=3.85\;atm\label{1.1.44}\]
The total pressure is the sum of the two partial pressures:
\[P_{\rm tot}=P_{\rm He}+P_{\rm O_2}=\rm(196.2+3.85)\;atm=200.1\;atm\label{1.1.45}\]
Exercise \(\PageIndex{5}\)
A cylinder of compressed natural gas has a volume of 20.0 L and contains 1813 g of methane and 336 g of ethane. Calculate the partial pressure of each gas at 22.0°C and the total pressure in the cylinder.
Answer
\(P_{CH_4}=137 \; atm\); \(P_{C_2H_6}=13.4\; atm\); \(P_{tot}=151\; atm\)
Mole Fractions of Gas Mixtures
The composition of a gas mixture can be described by the mole fractions of the gases present. The mole fraction (\(X\)) of any component of a mixture is the ratio of the number of moles of that component to the total number of moles of all the species present in the mixture (\(n_{tot}\)):
\[x_A=\dfrac{\text{moles of A}}{\text{total moles}}= \dfrac{n_A}{n_{tot}} =\dfrac{n_A}{n_A+n_B+\cdots}\label{1.1.46}\]
The mole fraction is a dimensionless quantity between 0 and 1. If \(x_A = 1.0\), then the sample is pure \(A\), not a mixture. If \(x_A = 0\), then no \(A\) is present in the mixture. The sum of the mole fractions of all the components present must equal 1.
To see how mole fractions can help us understand the properties of gas mixtures, let’s evaluate the ratio of the pressure of a gas \(A\) to the total pressure of a gas mixture that contains \(A\). We can use the perfect gas law to describe the pressures of both gas \(A\) and the mixture: \(P_A = n_ART/V\) and \(P_{tot} = n_tRT/V\). The ratio of the two is thus
\[\dfrac{P_A}{P_{tot}}=\dfrac{n_ART/V}{n_{tot}RT/V} = \dfrac{n_A}{n_{tot}}=x_A \label{1.1.47}\]
Rearranging this equation gives
\[P_A = x_AP_{tot} \label{1.1.48}\]
That is, the partial pressure of any gas in a mixture is the total pressure multiplied by the mole fraction of that gas. This conclusion is a direct result of the perfect gas law, which assumes that all gas particles behave ideally. Consequently, the pressure of a gas in a mixture depends on only the percentage of particles in the mixture that are of that type, not their specific physical or chemical properties. By volume, Earth’s atmosphere is about 78% \(N_2\), 21% \(O_2\), and 0.9% \(Ar\), with trace amounts of gases such as \(CO_2\), \(H_2O\), and others. This means that 78% of the particles present in the atmosphere are \(N_2\); hence the mole fraction of \(N_2\) is 78%/100% = 0.78. Similarly, the mole fractions of \(O_2\) and \(Ar\) are 0.21 and 0.009, respectively. Using Equation \(\ref{1.1.48}\), we therefore know that the partial pressure of N2 is 0.78 atm (assuming an atmospheric pressure of exactly 760 mmHg) and, similarly, the partial pressures of \(O_2\) and \(Ar\) are 0.21 and 0.009 atm, respectively.
Example \(\PageIndex{5}\): Exhaling Composition
We have just calculated the partial pressures of the major gases in the air we inhale. Experiments that measure the composition of the air we exhale yield different results, however. The following table gives the measured pressures of the major gases in both inhaled and exhaled air. Calculate the mole fractions of the gases in exhaled air.
| Inhaled Air / mmHg | Exhaled Air / mmHg | |
|---|---|---|
| \(P_{\rm N_2}\) | 597 | 568 |
| \(P_{\rm O_2}\) | 158 | 116 |
| \(P_{\rm H_2O}\) | 0.3 | 28 |
| \(P_{\rm CO_2}\) | 5 | 48 |
| \(P_{\rm Ar}\) | 8 | 8 |
| \(P_{tot}\) | 767 | 767 |
Strategy:
Calculate the mole fraction of each gas using Equation \(\ref{1.1.48}\).
Solution:
The mole fraction of any gas \(A\) is given by
\[x_A=\dfrac{P_A}{P_{tot}}\label{1.1.49}\]
where \(P_A\) is the partial pressure of \(A\) and \(P_{tot}\) is the total pressure. For example, the mole fraction of \(CO_2\) is given as:
\[x_{\rm CO_2}=\rm\dfrac{48\;mmHg}{767\;mmHg}=0.063\label{1.1.50}\]
The following table gives the values of \(x_A\) for the gases in the exhaled air.
| Gas | Mole Fraction |
|---|---|
| \({\rm N_2}\) | 0.741 |
| \({\rm O_2}\) | 0.151 |
| \({\rm H_2O}\) | 0.037 |
| \({\rm CO_2}\) | 0.063 |
| \({\rm Ar}\) | 0.010 |
Exercise \(\PageIndex{6}\)
Venus is an inhospitable place, with a surface temperature of 560°C and a surface pressure of 90 atm. The atmosphere consists of about 96% CO2 and 3% N2, with trace amounts of other gases, including water, sulfur dioxide, and sulfuric acid. Calculate the partial pressures of CO2 and N2.
Answer
\(P_{\rm CO_2}=\rm86\; atm\); \(P_{\rm N_2}=\rm2.7\;atm\)

