3.5: Isotopes
- Page ID
- 85148
- Calculate subatomic particles (protons, neutrons, and electrons) for any element by looking at the periodic table.
- Calculate subatomic particles (protons, neutrons, and electrons) for any element by looking at symbol-mass and A/Z format.
- Understand how isotopes differ in particles and mass.
- Identify the most abundant isotope when given specific values.
- Calculate the atomic mass of an element from the masses and relative percentages of the isotopes of the element.
- Define LEU/HEU with percentages and applications.
Isotopes are atoms of the same element that contain different numbers of neutrons. For these species, the number of electrons and protons remains constant. This difference in neutron amount affects the atomic mass (A) but not the atomic number (Z). In a chemical laboratory, isotopes of an element appear and react the same. For this reason, it is difficult to distinguish between an atom's isotopes. In contrast, nuclear scientists can identify and separate different types of atomic nuclei (Figure \(\PageIndex{1}\)). The technology required for this process is more sophisticated than what could be found in a typical chemical laboratory.
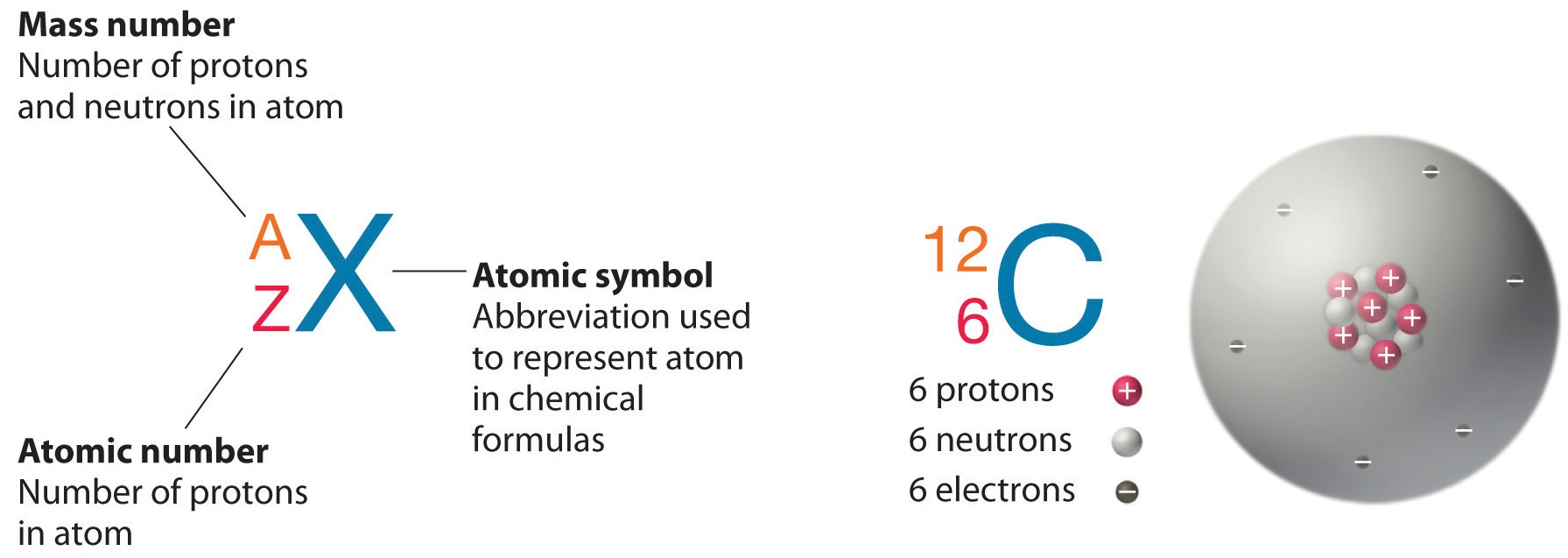
The element carbon (\(\ce{C}\)) has an atomic number of 6, which means that all neutral carbon atoms contain 6 protons and 6 electrons. In a typical sample of carbon-containing material, 98.89% of the carbon atoms also contain 6 neutrons, so each has a mass number of 12. An isotope of any element can be uniquely represented as \({}_Z^{A}X\)where X is the atomic symbol of the element. The isotope of carbon that has 6 neutrons is therefore \(\ce{_6^{12}C}\) The subscript indicating the atomic number is actually redundant because the atomic symbol already uniquely specifies Z. Consequently, it is more often written as \(\ce{^{12}C}\), which is read as “carbon-12.” Nevertheless, the value of \(Z\) is commonly included in the notation for nuclear reactions because these reactions involve changes in \(Z\).
Most elements on the periodic table have at least two stable isotopes. For example, in addition to \(\ce{^{12}C}\), a typical sample of carbon contains 1.11% \(\ce{_6^{13}C}\), with 7 neutrons and 6 protons, and a trace of \(\ce{_6^{14}C}\), with 8 neutrons and 6 protons. The nucleus of \(\ce{_6^{14}C}\) is not stable, however, but undergoes a slow radioactive decay that is the basis of the carbon-14 dating technique used in archaeology. Many elements other than carbon have more than one stable isotope; tin, for example, has 10 isotopes. There are about twenty elements that exist in only one isotopic form (sodium and fluorine are examples of these). Most scientists cannot tell you how many isotopic forms exist unless they consult an isotopic table.
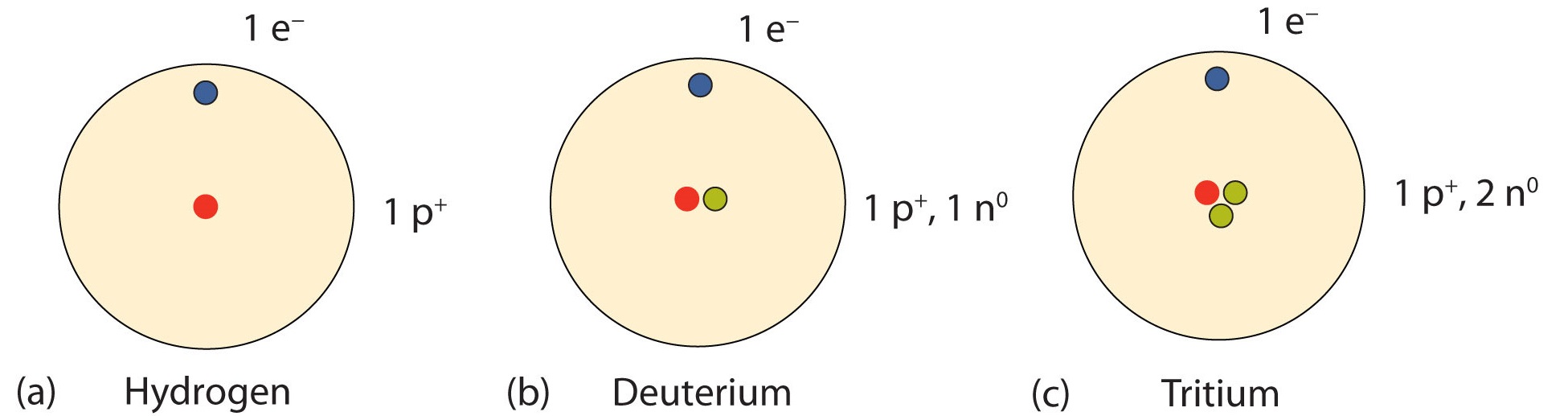
An important series of isotopes is found with hydrogen atoms. Most hydrogen atoms have a nucleus with only a single proton. About 1 in 10,000 hydrogen nuclei, however, also has a neutron; this particular isotope is called deuterium. An extremely rare hydrogen isotope, tritium, has 1 proton and 2 neutrons in its nucleus. Figure \(\PageIndex{2}\) compares the three isotopes of hydrogen.
There are currently over 3,500 isotopes known for all the elements. When scientists discuss individual isotopes, they need an efficient way to specify the number of neutrons in any particular nucleus. A/Z and symbol-mass formats (refer to Section 3.4) can be used to display periodic table information. When viewing either of these two notations, isotopic differences can be obtained.
The discovery of isotopes required a minor change in Dalton’s atomic theory. Dalton thought that all atoms of the same element were exactly the same.
Look at the A/Z formats for the three isotopes of hydrogen in Table \(\PageIndex{1}\). Note how the atomic number (bottom value) remains the same while the atomic masses (top number) are varied. All isotopes of a particular element will vary in neutrons and mass. This variance in mass will be visible in the symbol-mass format of same isotopes as well.
| Common Name | A/Z formats | symbol-mass format | Expanded Name |
|---|---|---|---|
| Hydrogen | \(\mathrm{^{1}_{1}H}\) | \(\text{H-1}\) | hydrogen-1 |
| Deuterium | \(\mathrm{^{2}_{1}H}\) | \(\text{H-2}\) | hydrogen-2 |
| Tritium | \(\mathrm{^{3}_{1}H}\) | \(\text{H-3}\) | hydrogen 3 |
Using a periodic table, A/Z or symbol-mass formats can be utilized to determine the number of subatomic particles (protons, neutrons, and electrons) contained inside an isotope. When given either format, these mass values should be used to calculate the number of neutrons in the nucleus.
How many neutrons are in each atom?
- \(\ce{^{36}_{17}Cl}\)
- \(\ce{^{58}_{26}Fe}\)
- \(\ce{C}\)-14
Solution
- In \(\mathrm{^{36}_{17}Cl}\) there are 19 neutrons in this nucleus. To find this value, subtract A-Z or 36 − 17.
- In \(\mathrm{^{58}_{26}Fe}\) there are 32 neutrons in this nucleus. Again, subtract A-Z or 58-26.
- In this example, the C-14 represents symbol-mass format. Once the atomic number is located (look at periodic table), subtract 14-6. The final answer will be 8 neutrons.
For the species below, translate the A/Z format to symbol-mass. Then, calculate the number of subatomics for each atom.
- \(\ce{^{197}_{79}Au}\)
- \(\ce{^{23}_{11}Na}\)
- \(\ce{^{239}_{94}Pu}\)
- Answer a
-
Au-197 contains 79 protons, 79 electrons, and 118 neutrons.
- Answer b
-
Na-23 contains 11 protons, 11 electrons, and 12 neutrons.
- Answer c
-
Pu-239 contains 94 protons, 94 electrons, and 145 neutrons.
Calculating Atomic Mass
The atomic mass of an element is the weighted mass of all the naturally presented isotopes. On the periodic table, it is assumed that this mass has units of amu (atomic mass unit) which can be abbreviated by using the letter u. To determine the most abundant isotopic form of an element, compare given isotopes to the weighted average on the periodic table. For example, the three hydrogen isotopes (shown above) are H-1, H-2, and H-3. The atomic mass or weighted average of hydrogen is around 1.008 amu ( look again at the periodic table). Of the three hydrogen isotopes, H-1 is closest in mass to the weighted average; therefore, it is the most abundant. The other two isotopes of hydrogen are rare but are very exciting in the world of nuclear science.
Identify the true statements:
- Al-27 is more abundant than Al-25.
- An appropriate isotope of bromine could be Br-35.
- A chemist could easily distinguish between Cs-132 and Cs-133 by noting chemical and physical properties.
- Most scientists know that calcium has 24 isotopes.
- Answer a
-
This statement is true. Aluminum with a mass of 27 is closest to the mass on the periodic table. It would be more abundant than Al-25.
- Answer b
-
This statement is false. An appropriate mass number of an isotope of bromine would be in around 80 amu (atomic mass units), not 35 (which is the atomic number).
- Answer c
-
Chemists cannot distinguish between isotopes by looking at various properties. Most isotopes have similar solubilities, densities, and colors.
- Answer d
-
Unless a scientist works heavily with a particular atom, he or she is not aware of the many forms that cannot exist. They would need a reference guide to know how many natural and artificial isotopes exist for a particular element.
You can calculate the atomic mass (or average mass) of an element provided you know the relative abundances (the fraction of an element that is a given isotope), the element's naturally occurring isotopes, and the masses of those different isotopes. We can calculate this by the following equation:
\[\text{Atomic mass} = \left( \%_1 \right) \left( \text{mass}_1 \right) + \left( \%_2 \right) \left( \text{mass}_2 \right) + \cdots \label{eq1} \]
To confirm your answer, compare the calculated value to the weighted mass displayed on the periodic table.
An element's atomic mass can be calculated provided the relative abundances of the element's naturally occurring isotopes and the masses of those isotopes are known. If all the abundances are not provided, it is safe to assume that all numbers should add up to 100%.
Boron has two naturally occurring isotopes. In a sample of boron, \(20\%\) of the atoms are \(\text{B-10}\), which is an isotope of boron with 5 neutrons and mass of \(10 \: \text{amu}\). The other \(80\%\) of the atoms are \(\text{B-11}\), which is an isotope of boron with 6 neutrons and a mass of \(11 \: \text{amu}\). What is the atomic mass of boron?
Solution
Boron has two isotopes. We will use the Equation \ref{eq1}:
\[\text{Atomic mass} = \left( \%_1 \right) \left( \text{mass}_1 \right) + \left( \%_2 \right) \left( \text{mass}_2 \right) + \cdots \nonumber \]
Substitute these into the equation, and we get:
\[\begin{align} \text{Atomic mass} &= \left( 0.20 \right) \left( 10 \right) + \left( 0.80 \right) \left( 11 \right) \nonumber \\ &= 10.8 \: \text{amu}\nonumber \end{align}\nonumber \]
The mass of an average boron atom, and thus boron's atomic mass, is \(10.8 \: \text{amu}\).
Neon has three naturally occurring isotopes. In a sample of neon, \(90.92\%\) of the atoms are \(\ce{Ne}\)-20, which is an isotope of neon with 10 neutrons and a mass of \(19.99 \: \text{amu}\). Another \(0.3\%\) of the atoms are \(\ce{Ne}\)-21, which is an isotope of neon with 11 neutrons and a mass of \(20.99 \: \text{amu}\). The final \(8.85\%\) of the atoms are \(\ce{Ne}\)-22, which is an isotope of neon with 12 neutrons and a mass of \(21.99 \: \text{amu}\). What is the atomic mass of neon?
Solution
Neon has three isotopes. We will use the equation:
\[\text{Atomic mass} = \left( \%_1 \right) \left( \text{mass}_1 \right) + \left( \%_2 \right) \left( \text{mass}_2 \right) + \cdots \nonumber \]
Substitute these into the equation, and we get:
\[\begin{align*} \text{Atomic mass} &= \left( 0.9092 \right) \left( 19.99 \right) + \left( 0.003 \right) \left( 20.99 \right) + \left( 0.0885 \right) \left( 21.99 \right) \\ &= 20.18 \: \text{amu} \end{align*} \]
The mass of an average neon atom is \(20.18 \: \text{amu}\)
During the Manhattan project, the majority of federal funding dedicated the separation of uranium isotopes. The two most common isotopes of uranium are U-238 and U-235. About 99.3% of uranium is of the U-238 variety, this form is not fissionable and will not work in a nuclear weapon or reaction. The remaining .7% is U-235 which is fissionable but first had to be separated from U-238. This separation process is called enrichment. During World War II, a nuclear facility was built in Oak Ridge, Tennessee to accomplish this project. At the time, the enrichment process only produced enough U-235 for one nuclear weapon. This fuel was placed inside the smaller of the two atomic bombs (Little Boy) dropped over Japan.

Uranium is a natural element that can be found in several different countries. Countries that do not have natural uranium supplies would need to obtain it from one of the countries below. Most nuclear reactors that provide energy rely on U-235 as a source of fuel. Fortunately, reactors only need 2-5% U-235 for the production of megawatts or even gigawatts of power. If the purification process exceeds this level, then it is likely a country is focusing on making nuclear weapons. For example, Manhattan Project scientists enriched U-235 up to 90% in order to produce the Little Boy weapon.
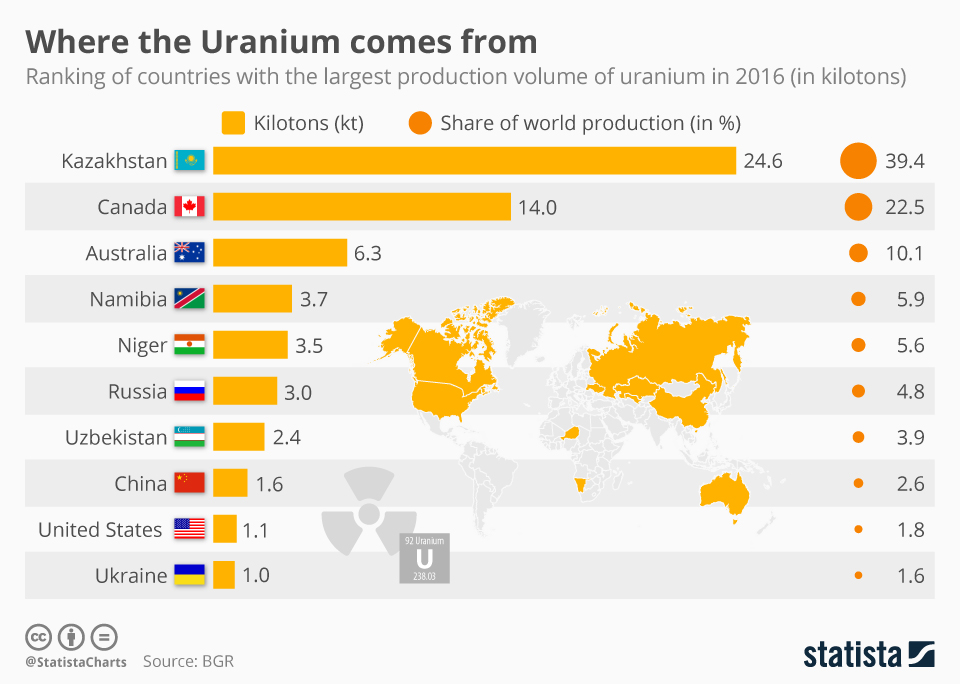
Abbreviations like HEU (highly enriched uranium) and LEU (low-enriched uranium) are used frequently by nuclear scientists and groups. HEU is defined as being over 20% pure U-235 and would not be used in most commercial nuclear reactors. This type of material is used to fuel larger submarines and aircraft carriers. If the purification of U-235 reaches 90%, then the HEU is further classified as being weapons-grade material. This type of U-235 could be used to make a nuclear weapon (fission or even fusion-based). As for LEU, its U-235 level would be below this 20% mark. LEU would be used for commercial nuclear reactors and smaller, nuclear-powered submarines. LEU is not pure enough to be used in a conventional nuclear weapon but could be used in a dirty bomb. This type of weapon uses conventional explosives like dynamite to spread nuclear material. Unlike a nuclear weapon, dirty bombs are not powerful enough to affect large groups of buildings or people. Unfortunately, the spread of nuclear material would cause massive chaos for a community and would result in casualties.
Need More Practice?
- Turn to Section 3.E of this OER and work problems #3, #6, #7, and #10.


