2.4: Temperature
- Page ID
- 85141
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Learn about the various temperature scales that are commonly used in chemistry and other cultures.
- Memorize temperature equations for Celsius and Fahrenheit conversions.
- Differentiate between various thermometers (alcohol or mercury-based).
- Understand how body temperature can vary.
- Provide some examples of how cryogenics is used in the real-world.
Temperature Scales
One of the fundamental quantities in science is temperature, which is a measure of the average amount of energy of motion, or kinetic energy, a system contains. Temperatures are expressed using scales that use units called degrees. There are three scales used for reporting temperatures. Figure \(\PageIndex{1}\) compares the three temperature scales.
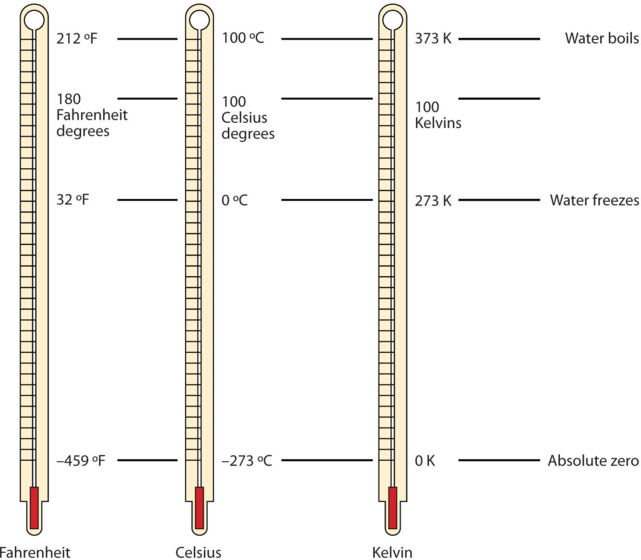
In the United States, the commonly used temperature scale is the Fahrenheit scale (symbolized by °F and spoken as “degrees Fahrenheit”). On this scale, the freezing point of liquid water (the temperature at which liquid water turns to solid ice) is 32 °F, and the boiling point of water (the temperature at which liquid water turns to steam) is 212 °F.
Science also uses other scales to express temperature. For example, the Celsius scale (symbolized by °C and spoken as “degrees Celsius”) defines 0°C as the freezing point of water and 100 °C as the boiling point of water. This scale is divided into 100 divisions between these two landmarks and extended higher and lower as well. By comparing the Fahrenheit and Celsius scales, a conversion between the two scales can be determined:
\[^{\circ}C= \left(^{\circ}F-32\right)\times \dfrac{5}{9} \label{F2C} \]
\[^{\circ}F= \left(^{\circ}C\times \dfrac{9}{5}\right)+32 \label{C2F} \]
Note that science uses the Celsius and Kelvin scales almost exclusively; virtually no practicing chemist expresses laboratory-measured temperatures with the Fahrenheit scale. (In fact, the United States is one of the few countries in the world that still uses the Fahrenheit scale on a daily basis. People driving near the borders of Canada or Mexico may pick up local radio stations on the other side of the border that express the daily weather in degrees Celsius, so do not get confused by their weather reports.)
- What is 98.6°F in degrees Celsius?
- What is 25.0°C in degrees Fahrenheit?
Solution
- Using Equation \ref{F2C}, we have
\[\begin{align*} ^{\circ}C &= (98.6-32)\times \dfrac{5}{9} \\[5pt] &=66.6\times \dfrac{5}{9} \\[5pt] &= 37.0^{\circ}C \end{align*} \]
- Using Equation \ref{C2F}, we have
\[\begin{align*} ^{\circ}F &= (25.0\times \dfrac{9}{5})+32 \\[5pt] &= 45.0+32 \\[5pt] &=77.0^{\circ}F \end{align*} \]
For more examples of how to perform these types of problems, click on this video to see your professor in action.
- Convert 0°F to degrees Celsius.
- Convert 212°C to degrees Fahrenheit.
- Answer a
-
−17.8°C
- Answer b
-
414°F
The fundamental unit of temperature in SI is the Kelvin (K). The Kelvin temperature scale (note that the name of the scale capitalizes the word Kelvin, but the unit itself is lowercase) uses degrees that are the same size as the Celsius degree, but the numerical scale is shifted up by 273.15 units. That is, the conversion between the Kelvin and Celsius scales is as follows:
\[K=^{\circ}C+273.15 \label{C2K} \]
For most purposes, it is acceptable to use 273 instead of 273.15 in Equation \ref{C2K}.
Note that the Kelvin scale does not use the word degrees; a temperature of 295 K is spoken of as “two hundred ninety-five kelvin” and not “two hundred ninety-five degrees Kelvin.”
The reason that the Kelvin scale is defined this way is that there exists a minimum possible temperature called absolute zero (zero Kelvin). The Kelvin temperature scale is set so that 0 K is absolute zero, and the temperature is counted upward from there. Normal room temperature is about 295 K, as seen in the following example.
If the normal room temperature is 72.0°F, what is room temperature in degrees Celsius and kelvin?
Solution
First, we use Equation \ref{F2C} to determine the temperature in degrees Celsius:
\[\begin{align*} ^{\circ}C &= (72.0-32)\times \dfrac{5}{9} \\[5pt] &= 40.0\times \dfrac{5}{9} \\[5pt] &= 22.2^{\circ}C \end{align*} \]
Then we use Equation \ref{C2K} to determine the temperature in the Kelvin scale:
\[\begin{align*} K &= 22.2^{\circ}C+273.15 \\[5pt] &= 295.4K \end{align*} \]
So, room temperature is about 295 K.
Normal body temperature is defined as being 98.6°F (+/- 1.0°F). To determine body temperature, thermometers can be placed inside or on the surface of the body. The two best methods of obtaining body temperature are placing the thermometer either under the tongue or inside the rectum. Typically, children are capable of holding a thermometer in their mouths around the age of four (have fun before that age).
Fever is defined as body temperature being above 100°F (adults). High fever status occurs at and above 104°F. For adults, these adults should seek medical attention immediately if the fever exceeds 104°F. For children, these values are much lower.
Hyperthermia (inability of the body to regulate heat) occurs when normal body temperature is exceeded. Conditions that can cause hyperthermia are fever (infection), heat stroke, thyroid disorders, heart attack, or traumatic injury. Medications for cancer, arthritis, and thyroid patients can cause the body temperature to rise. Symptoms of hyperthermia include sweating, confusion, nausea, and dizziness.
Hypothermia (exposure to cold environments) occurs when normal body temperature dips below 95.0°F. When this occurs, the affected person(s) should seek immediate medical attention. During hypothermia, the body has problems producing heat. Medical conditions like diabetes, infection, and thyroid dysfunction can cause hypothermia. Watch this video of American Marines attempting to survive extreme environments. Symptoms of this condition involve shivering, confusion, and sluggish behavior.
Treating hyperthermia could involve hydrating a patient. If a fever is due to infection, analgesics (like Tylenol, Advil, aspirin, or Aleve) can help alleviate fever. Placing someone in a cool bath can also relieve symptoms.
To combat hypothermia, one must remove wet clothing, redress in warm materials, and participate in physical movement.
The Science of Cryogenics
Cryogenics is branch of physics that incorporates the production and effects of substances at temperatures ranging between -150ºC to -273°C. In the late 1870's, cryogenic science began with the cooling of gaseous oxygen. At -183ºC, O2 condensed from a clear gas into a blue liquid. Changing the state of oxygen enables it to be transported easier. Both the aircraft and medical industries rely on the liquid form of this molecule to provide breathable oxygen for pilots, travelers, and patients.

Besides oxygen, other gases have been condensed as well. These permanent gases, meaning these substances normally exist in the gaseous state, include nitrogen (N2), hydrogen (H2), chlorine (Cl2), and helium (He). By manipulating pressure and/or temperature, many chemists and physicists have attempted to produce the lowest, theoretical temperature possible. At absolute zero (-273°C or 0 K), the particles of a material have a minimum kinetic energy. Click on this video to determine if scientists can ever reach absolute zero in their laboratories.
With a boiling point of -196°C (-321°F), liquid nitrogen has a variety of cryogenic uses. This clear, odorless liquid is used widely in the field of dermatology. For patients that have warts, skin tags (see image below), or precancerous moles, physicians can spray a selected area of skin. Typically, the unwanted skin lesion will fall off the body after being exposed to this cryogenic material. If this does not occur, then the dermatologist will use a scalpel to remove the frozen area of skin.

Liquid N2 is also utilized to freeze biological samples. Fertility clinics freeze semen, eggs, and embryos that can be used at a later date for couples who chose to undergo InVitro Fertilization (IVF). Umbilical cord blood and stem cells can be preserved in liquid nitrogen for future applications.
Culinary Arts employ liquid nitrogen for preparing various dishes and interesting cocktails. In the following video, chefs are freezing components of salads and desserts for their customers. When using liquid nitrogen for any application, chemists, chefs, and other individuals should protect their skin and eyes from the extremely cold (-196ºC) temperature. Wearing thick rubber gloves and goggles can prevent frostbite. When ingesting materials that have been frozen with liquid nitrogen, there is concern that internal burns can occur. Lastly, indoor use of liquid nitrogen could induce asphyxiation. Kitchens and labs should have adequate ventilation to ensure sufficient oxygen remains in the atmosphere.
References
Need More Practice?
- Turn to Section 2.E of this OER and work problems #4, #7, and #10.
Contributors and Attributions
- Hayden Cox (Furman University, Class of 2018)


