2: Atoms—They make up everything!
- Page ID
- 188930
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Using atoms to store renewable energy!
Sossina Haile, Professor of Materials Science and Engineering at Northwestern University, and her students (see below) are using chemistry to address one of the greatest shortcomings in renewable energy—storage and transport. They are developing technologies to create liquid fuel by splitting water into hydrogen gas or combining water and carbon dioxide using solar energy. She invented the solid acid fuel cell and her record-setting proton-conducting fuel cell made the news. Haile and her students used crazy mixtures of a bunch of elements to create catalysts in highly efficient and stable devices. One component of the device contains Pr, Ba, Sr, Co, Fe, and O and another part contains Ni, Ba, Zr, Ce, Y, Yb, and O. They have to get the perfect mixture of all of these elements to give the excellent performance they have achieved. Read more in "Bottling the Sun".
Goals and expectations
- Interconvert properties of an element using unit conversions, density, and atomic masses.
- Describe the difference between the following on the macroscopic and microscopic scales: an element, a compound, a solution, a homogeneous mixture, a heterogeneous mixture.
- Relate the number of protons, neutrons, and electrons to descriptors of that atom.
- Use the concepts of isotopic mass and isotopic abundance to relate the properties of isotopes.
On an exam, you will only be provided with a periodic table. All other necessary information should be in your head!
Transforming one descriptor of a substance to another using a conversion factor
Starter video This video by Prof. Plass walk through doing a unit conversion, which is just one example of taking a value (a number plus units, plus the identity of the substance) and converting it to another form using a conversion factor (a ratio of two equal things).
Video of more complex problem Here is a video by Prof. Plass doing a more complicated example.
Practice problems and readings for each goal
Goal #1: Interconvert properties of an element using unit conversions, density, and atomic masses.
Achieving this goal requires:
- Picturing matter as consisting of tiny particles called atoms.
- Knowing the following terms and units:
- Atoms and elements
- Volume (measured in L or cm3)
- Mass (measured in g)
- Density = mass/volume (g/L, g/mL, etc)
- Metric prefixes. These are the ones you will be expected to know:
|
Name (abbreviation) |
Example conversion(s) |
|
kilo (k) |
1 kg = 1000 g AND 10-3 kg = 1 g |
|
centi (c) |
102 cm = 1 m |
|
milli (m) |
103 mL = 1 L |
|
micro (μ) |
106 μmol = 1 mol |
|
nano (n) |
109 nm = 1 m AND 10-9 nm = 1 m |
|
pico (p) |
1012 pm = 1 m AND 10-12 pm = 1 m |
- Being able to perform a mathematical transformation of one descriptor of a substance to another using a conversion factor. See above for crash course.
- Interpretation of graphical data in advanced applications.
Exercise \(\PageIndex{1}\)
1. Which of the following pictures represents each of the following substance types? Justify your answer in a few sentences.
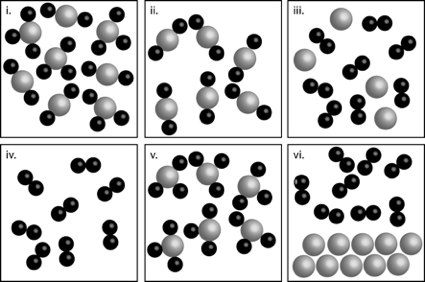
An element
A pure compound
A heterogeneous mixture
A solution
- Answer
-
Add texts here. Do not delete this text first.
An element = iv
A pure compound = v and ii
A heterogeneous mixture = vi
A solution = iii and i
Goal #2: Describe the difference between the following on the macroscopic and microscopic scales: an element, a compound, a solution, a homogeneous mixture, a heterogeneous mixture.
Achieving this goal requires:
- Know the definitions of an element, a compound, a solution, a homogeneous mixture, a heterogeneous mixture.
- Relate these definitions to representations of the microscopic behavior, like these:
- Relate these definitions to macroscopic behavior.
- Recognize the microscopic representations of phase change processes (boiling, freezing, dissolution).
|
Starting practice: |
Do if needed: OS Chapter 1 (9-19) |
Further resources*: If you find any additional resources you like, please forward them to Prof. Plass! |
Goal #3: Relate the number of protons, neutrons, and electrons to descriptors of that atom.
Achieving this goal requires:
- Recognizing the atomic # (Z) on the periodic table and relating this to the number of protons.
- Knowing the definitions of…
- Mass number
- Isotope
- Integer charge
- Ion
- Cation
- Anion
- Nucleus
|
Starting practice: |
Extra: Chemlibretext 1-5 |
Further resources*: If you find any additional resources you like, please forward them to Prof. Plass! |
Goal #4: Use the concepts of isotopic mass and isotopic abundance to relate the properties of isotopes.
- Achieving this goal requires:
- Knowing the definitions of:
- Isotopic mass
- Isotopic abundance (in fractional and % forms)
- Average atomic mass = sum of (isotopic mass)x(fractional isotopic abundance)
- Using isotopic mass and isotopic abundance to perform a mathematical transformation of one value of an isotope to another using a conversion factor.

