3.1.3: Breaking the Octet rule in Hypervalent Atoms

The octet rule applies well to atoms in the second row of the periodic table, where a full valence shell includes eight electrons with an electron configuration of \(s^2p^6\). Even elements in the third and fourth row are known to follow this rule sometimes, but not always. In larger atoms, where \(n\geq3\) the valence shell contains additional subshells: the \(d, f, g...\) subshells. Therefore, atoms with \(n\geq3\) can have higher valence shell counts by "expanding" into these additional subshells. When atoms contain more than eight electrons in their valence shell, they are said to be hypervalent. Hypervalency allows atoms with \(n\geq3\) to break the octet rule by having more than eight electrons. This also means they can have five or more bonds; something that is nearly unheard of for atoms with \(n\leq2\). Complete the exercises below to see examples of molecules containing hypervalent atoms.

Exercise \(\PageIndex{1}\)

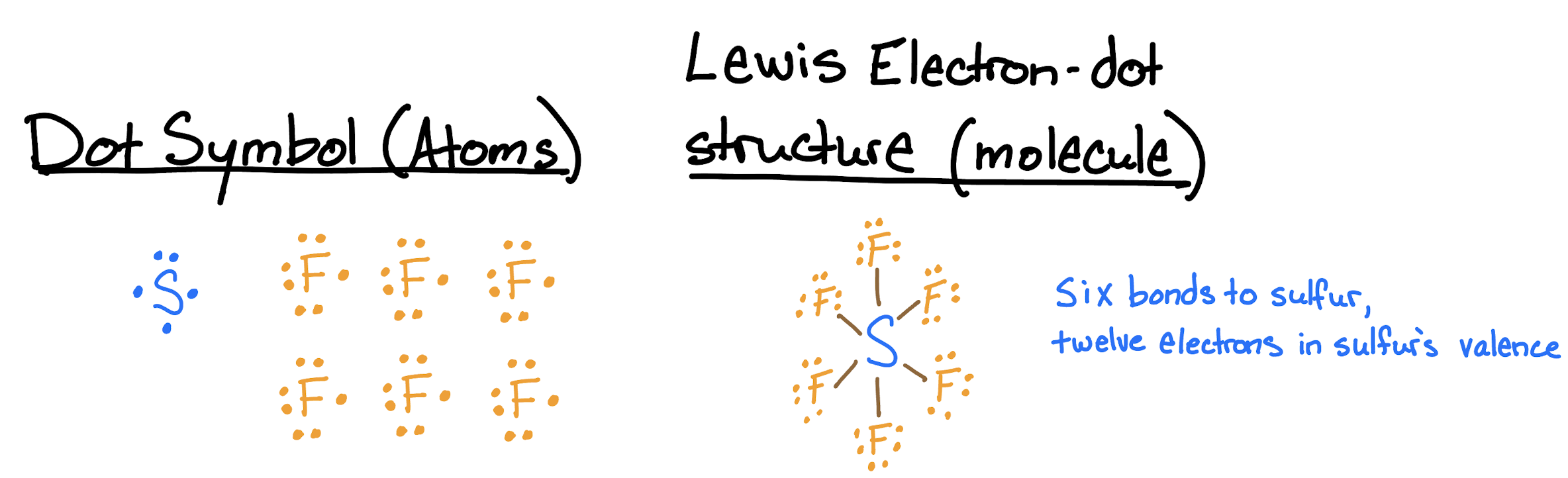
Draw the Lewis structures for sulfur hexafluoride (\(\ce{SF6}\)).

Answer

Each fluorine atom has one valence electron and will make one bond each. The sulfur has six valence electrons, and must make six bonds to form a molecule with the six fluorine atoms. The molecular structure has six bonds to sulfur, with twelve valence electrons. The sulfur is hypervalent.

Exercise \(\PageIndex{1}\)

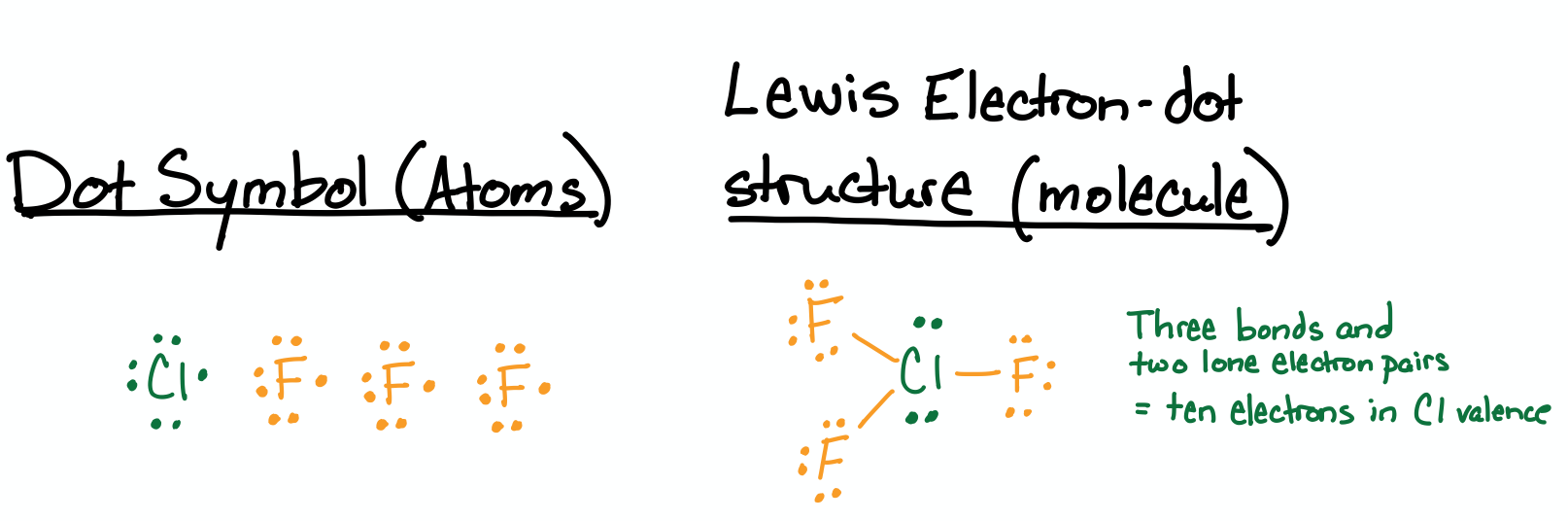
Draw the Lewis structure for chlorine trifluoride (\(\ce{ClF3}\)).

Answer

All atoms are halogens and each has seven valence electrons. Chlorine is capable of hypervalency because it is in the third row of the periodic table; however fluorine cannot have more than eight valence electrons in its valence because it is in the second row. The structure has the three fluorine atoms bonded to a central chlorine atom. The chlorine has a valence of ten electrons due to its three bonds and two lone pairs.

.

Is hypervalency real? Not exactly. Hypervalency is a concept associated with hybrid orbital theory and Lewis theory. It's useful for some simple things, like predicting how atoms are connected and predicting molecular shape. But the idea that the d-orbitals are involved in bonding isn't accurate according to wave mechanics.

For main group molecules, chemists (like Pauling) thought a long time ago that hypervalence is due to expanded s²p⁶ octets. The consensus is now clear that d orbitals are NOT involved in bonding in molecules like SF₆ any more than they are in SF₄ and SF₂. In all three cases, there is a small and roughly identical participation of d-orbitals in the wavefunctions. This has been established in both MO and VB theory. However, using hybrid orbitals with d-orbital contributions equips us with a language which can pragmatically describe the geometries of highly coordinated substances.

While hybrid orbitals are a powerful tool to describe the geometries and shape of molecules and metal complexes, in "real" molecules their significance may be debated. Often a more realistic molecular orbitals approach is needed. However, from an epistemologically simple point of view, bonding theories can only be judged by their predictions. To the extent that hybridization can explain the shapes of PF₅ and SF₆, valence bond theory is a perfectly good theory. To the extent that if you write out the valence bond wavefunction using hybridized orbitals and calculate energies and other properties à la Pauling (i.e., ionization energy and electron affinities) and find them to be off from experimental results (by tens of kcals/mol), then valence bond theory is not accurate.

Bonding theories can only be judged by the accuracy of their predictions

No-bond resonance

An alternative way to visualize hypervalency is using resonance structures in which there is a bond order of zero between two of the atoms (i.e. including ionic bonds). This concept of no-bond resonance is important in understanding the bonding in many halogen- and hydrogen-containing compounds. The idea is illustrated below for the generic molecule X-Y-Z, where Z might be an electronegative halogen atom such as F. By moving the bonding electrons from the Y-Z bond onto the Z atom, and moving a lone pair from X into the X-Y bond, we generate the resonance structure shown on the right in which all atoms remain octet, but there is no bond between Y and Z.

It is important to recognize in this example that the no-bond form is only one resonance structure, and therefore the Z atom is still bound to Y. If the two resonance structures in this example have the same energy, we would expect the X-Y bond order to be 1.5 and the Y-Z bond order to be 0.5. Therefore the Y-Z bond should be longer than it is in a compound where the bond order is one, and it should be relatively easy to break the Y-Z bond.

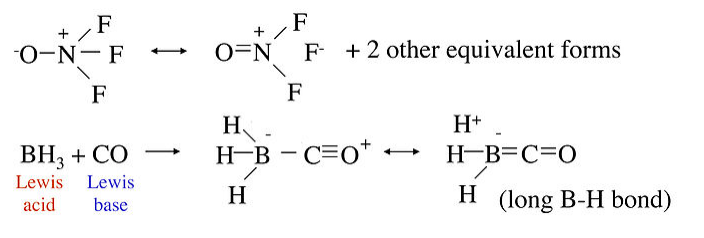
Some molecular examples of no-bond resonance are shown below. In the molecule ONF₃, the N-F bond is unusually long relative to the N-F bond in NF₃, in which the bond order is 1. This can be explained by the no-bond resonance forms shown on the right. Similarly, in the Lewis acid-base adduct formed by combining BH₃ with CO, we can explain the long B-H bonds using no-bond resonance forms that place a partial positive charge on the H atoms.

No-bond resonance is often used to provide an octet bonding picture for so-called hypervalent compounds, which are compounds that appear to have more than 8 valence electrons in the bonding shell of the central atom. For example, we can consider two different valence bond structures for the triiodide ion, I₃^-, which is formed by reaction of I^- with I₂ in water:

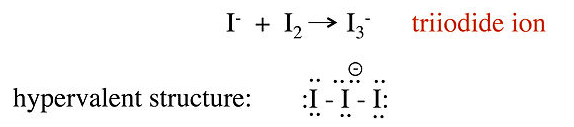
In this structure, the central iodine atom has 10 electrons in its valence shell, in violation of the octet rule. Raman spectra of the triiodide ion show that the I-I bond is weaker than the I-I single bond in I₂, suggesting that this picture is not an accurate description of the bonding. A better representation of I₃^- can be obtained with no-bond resonance structures, as shown below.

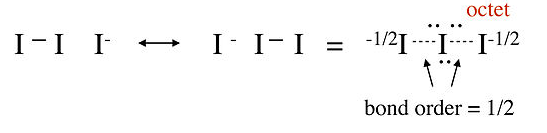
The deep blue color of starch-iodine solutions results from the complexation of linear polyiodide ions (In^-) by the starch (amylose) left-handed helix. The interior of the helix is hydrophobic. In electron donor solvents such as ethanol and water, I2 and salts of I3^- have a brown color, the result of a charge transfer interaction between the solvent and solute.^[2]^[3]

We can draw a similar picture for the XeF₂ molecule, which has the same number of valence electrons as I₃^-. This picture is consistent with XPS data, which show a partial negative charge on the F atoms, as well as vibrational spectra, which show that the Xe-F bond is weaker in XeF₂ than it is in the singly-bonded cation Xe-F⁺.

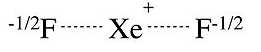
Other well known examples of hypervalent compounds are PF₅, P(CH₃)₅, and SF₆, as well as oxyacids such as H₂SO₄ and HClO₄. The hypervalent structure is often drawn for these molecules, with the explanation that d-orbitals on the central atom contribute to the bonding in dsp³ and d²sp³ hybrids for 5- and 6-coordinate molecules, respectively. However, realistic molecular orbital calculations show that the phosphorus and sulfur 3d orbitals are too high in energy to contribute significantly to bonding in PF₅ and SF₆. For these molecules, we can use no-bond resonance to make reasonable octet structures that predict polar bonds between the central atom and F.

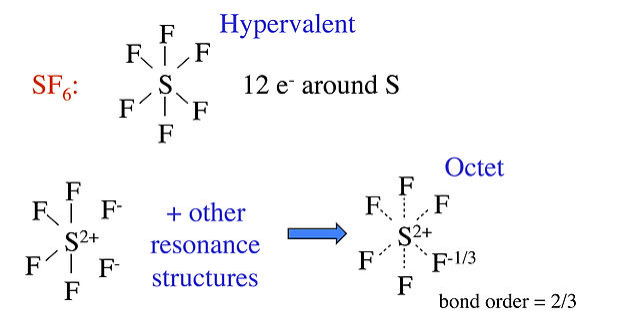
Space-filling model of sulfur hexafluoride. SF6 is surprisingly unreactive with water, relative to other compounds that contain S-F bonds. The tight packing of F atoms around S prevents nucleophilic attack by water.

In other cases, such as P(CH₃)₅, the octet structure is unreasonable because it suggests a polar bond between P and C, with a partial negative charge on C. Further, in the case of oxyacids such as H₂SO₄ and HClO₄, X-ray crystallographic data establish that the S-O and Cl-O bonds are shorter for the oxygen atoms not bonded to hydrogen, which is more consistent with the hypervalent picture:

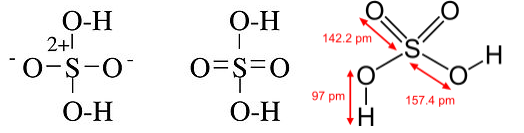
The question of whether hypervalency and the octet rule are really useful descriptions of the bonding in these compounds has been considered in a number of computational studies, which have used increasingly accurate quantum mechanical calculations to determine the number of electrons associated with the central atom. In a 2002 study, Gillespie and Silvi^[4] found that the population of the valence shell is greater than eight for compounds with electropositive ligands, such as P(CH₃)₅, and less than eight for compounds such as PF₅. They concluded that these valence electron shell populations depend primarily on the coordination numbers and electronegativities of the central atoms and their ligands, and that there is no fundamental difference between the bonding in hypervalent and non-hypervalent (Lewis octet) molecules. This reminds us that the octet rule is not a law of nature, but rather an empirical rule that is useful within certain limits.