5.2.2: Rotational Transitions Accompany Vibrational Transitions

The infrared region (IR) of the electromagnetic spectrum is of interest to chemists because it corresponds to the energy of the vibrational modes of molecules (specifically the region between 4000 to 400 \(cm^{-1}\)). When the frequency of infrared radiation matches the vibrational frequency of a molecule, the molecule can become vibrationally excited by transitioning from the vibrational ground state to a vibrational excited state.In the case of diatomic molecules, like HCl, there is only one vibrational mode. Thus, we might expect one vibrational absorption band in the IR spectrum.

However, in the gas phase IR spectrum of HCl, there is a complex pattern of bands (see Figure \(\PageIndex{1}\)). The structure that is observed in the IR spectrum of HCl  was one of the early pieces of evidence supporting quantum mechanics and the idea that molecular states (like vibrational and rotational states) are quantized. The person who first measured a high-resolution spectrum like the one shown in Figure \(\PageIndex{1}\), and who used this spectrum experimental confirmation of the Franck–Condon principle, was a Elmer Imes (click here for Wikipedia - unfortunately, we couldn't find a public domain photo of him, but google his name and you'll find him!). Imes is best known for his collaboration with James Franck in 1926, where they conducted experiments on molecular spectra (like Figure \(\PageIndex{1}\)) and provided experimental confirmation of the Franck–Condon principle. This principle relates to the intensity distribution of vibrational transitions in molecular spectra. Imes was the first African American in the 20th century to gain a Ph.D., and he became a physics professor at Fisk University. Elmer Imes's work, along with that of his contemporaries, laid the foundation for our understanding of molecular structures and behaviors, particularly in the realm of rotational-vibrational spectroscopy. His contributions have had a lasting impact on the study of molecular physics and spectroscopy. You will follow in his footsteps during this module!

Figure \(\PageIndex{1}\). Gas phase FTIR spectrum of HCl. In this view, the data is plotted in a similar fashion as you may have seen in organic chemistry courses. The intensity is shown as % transmission on the Y axis and wavenumbers on the X axis. The X axis is plotted from high to low wavenumber. Figure used with permission from Wikipedia.

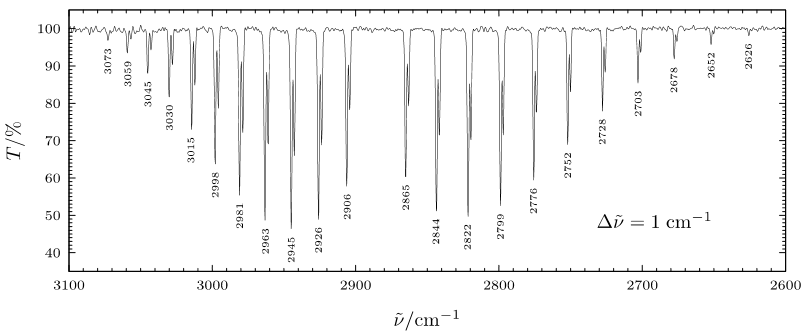
While every peak on the spectrum shown in Figure \(\PageIndex{1}\) represents a transition from the ground vibrational state to the first vibrational excited state, each represents a unique transition from one rotational state of the ground vibrational state to a different rotational state of the vibrational exited state. This coupling of rotational and vibrational states that appears in the IR spectrum in Figure \(\PageIndex{1}\) illustrates the quantized nature of molecular motions.

Models of Molecular Motion

To explain the spectrum shown above, we start by considering all the possible molecular motions and useing simple models to describe them

VIBRATIONAL motions and the HARMONIC OSCILLATOR model

The HCl molecule vibrates along the bond axis. We can treat the molecule's vibrations as those of a harmonic oscillator (ignoring anharmonicity). The energy of a vibration is quantized in discrete energies given by

\[E(\upsilon)=h\nu \left({\upsilon}+\dfrac{1}{2} \right) \text{ or  } \tilde{E}(\upsilon) = \tilde{\nu} \left({\upsilon}+\dfrac{1}{2} \right) \]

Where \(\upsilon\) is the vibrational quantum number and can have integer values 0, 1, 2, 3...etc., and \(\nu\) or \(\tilde{\nu}\) is the frequency of the vibration given by:

\[\nu=\dfrac{1}{2\pi}\left(\dfrac{k}{\mu}\right)^\dfrac{1}{2} \]

where \(k\) is the force constant and \(\mu\) is the reduced mass of a diatomic molecule with atom masses \(m_1\) and \(m_2\), given by

\[\mu=\dfrac{{m}_1{m}_2}{{m}_1+{m}_2} \label{reduced mass} \]

At room temperature, nearly 100% of the molecules are in their ground vibrational state \(\upsilon=0\) according to the Boltzman distribution. By convention, the ground vibrational state is indicated by a double prime (") while the exited state is indicated by a single prime (').

• Ground state: \(\upsilon"=0\), nearly homogeneous population in the ground state at room temp.
• First excited state: \(\upsilon'=1\)

At room temperature, the lowest energy vibrational state \(\upsilon= 0\) is populated, so \(\upsilon"=0\). Thus, the only reasonable transition is from \(\upsilon"=0\) to \(\upsilon'=1\), and \(\Delta \upsilon = +1\).

Figure \(\PageIndex{2}\): The potential energy (\(U\)) well of an 'ideal' harmonic oscillator. The well is defined by the function \(U=\frac{1}{2}kx^2\), where \(k\) is the force constant and \(x\) is the displacement from equilibrium bond length. The vibrational quantum numbers (\(\upsilon\)) are indicated for the first three vibrational energy levels. The transition between \(\upsilon=0\) to \(\upsilon=1\) is indicated by the magenta arrow. (Kathryn Haas; CC-BY-SA)

The harmonic oscillation is a useful approximation of a molecular vibration, but has key limitations:

• Due to equal spacing of the energy levels, all transitions would occur at the same frequency (i.e. you'd get a single line spectrum). However experimentally many lines are often observed (called overtones).
• The harmonic oscillator does not predict bond dissociation; you cannot break it no matter how much energy is introduced.

"Real" bond vibrations are anharmonic

The vibrational energy levels of a real molecule are not evenly spaced and are more like that shown in the illustration in Figure \(\PageIndex{3}\), where the energies are more closely spaced as \(\upsilon\) increases. However, the harmonic oscillator is a reasonable approximation at \(\upsilon=0\) and \(\upsilon=1\).

Figure \(\PageIndex{3}\): Illustration of vibrational energy levels predicted by the harmonic oscillator model and those of a real diatomic molecule. (Kathryn Haas; CC-BY-SA)

ROTATIONAL motions and the the RIGID ROTOR model

The HCl molecule also has rotational motions. We treat the molecule's rotations as those of a rigid rotor (ignoring centrifugal distortion from non-rigid rotor aspects). The energy of a rotation is also quantized in discrete levels given by

\[ E_J=\dfrac{h^2}{8\pi^2I} J(J+1) \]

In which \(J\) is the rotational quantum number with integer values 0, 1, 2, 3...etc., and \(I\) is the moment of inertia, given by

\[{I}=\mu{r}^2 \]

where \(\mu\) is the reduced mass (Equation \ref{reduced mass}) and \(r\) is the equilibrium bond length.

Experimentally, frequencies of light are measured (in units of \(cm^{-1}\)), so it is convinient to use these units in our expressions. The frequency can be divided by \(hc\) to give energy in units of wavenumbers. The expression for the rotational energy levels expressed in wavenumbers is \(\tilde{E}_J=\dfrac{E_J}{hc}=\dfrac{h}{8\pi^2cI} J(J+1)=\tilde{B}J(J+1)\). And, we can simplify the expression by defining the rotational constant (\tilde{B}\) as \[\tilde{B} = \frac{h}{8 \pi ^2 I c} \] 

This gives the allowed energies of rotation, in wavenumbers, as \[\tilde{E}_J=\tilde{B}J(J+1) \]

Tip: It is important to note in which units you are working. The frequencies and rotational constants can have different units (eg Hz or wavenumbers). To keep track, we are using the tilde \(\tilde{X}\) to indicate wavenumber units, but some texts don't do this - they always represent the rotational constant as \(B\), whether in frequency or wavenumbers. Just be sure you are paying attention and are using consistent units in your calcaulations.

Just as in the notations for vibrational states, the convention for notating rotational ground state is by a double prime (") while the exited state is indicated by a single prime ('). The lowest-energy rotational state is \(J" = 0\). Rotational energy levels are very close in energy (much closer than vibrational energy levels), and so at temperatures close to room temperature, there is enough energy so that higher-energy states are populated (e.g. \(J"=1, 2, 3...\) are also populated). The statistical probability of each rotational state being populated can be calculated using the Boltzmann distribution.

• Ground state: \(J"\); at room temperature there is heterogeneous population of the rotational states.
• Excited state: \(J'\); upon excitation we can also expect a heterogenous population of excited states.

The rotational energy states are closer in energy than vibrational energy states. And, real molecules undergo rotationas and vibrations simultaneously. Thus, one way to show the rotational energy levels is to superimpose them on a diagram of the harmonic oscillator vibrational energy levels, as is illustrated in Figure \(\PageIndex{3}\).

Figure \(\PageIndex{3}\): The rotational states are shown superimposed in the vibrational states. Rotational transitions are on the order of 1-10 cm^-1, while vibrational transitions are on the order of 1000 cm^-1. The difference of magnitude between the energy transitions allow rotational levels to be superimposed within vibrational levels. All ground state rotational states are indicated by \(J"\) in purple, and rotational states of the excited state are indicated by \(J'\) in orange. A transition with \(\Delta J = +1\) is indicated by the arrow on the left. A transition with \(\Delta J = -1\) is indicated by the arrow on the right. (Kathryn Haas; CC-BY-SA)

Combining rotational and vibrational models

Real molecules are rotating and vibrating simultaneously, and the rotational and vibrational states are coupled. We could express the energies of these motions (in wavenumbers) as a simple combination of rotational and vibrational motions:

\[\tilde{E}_{\upsilon, J} = \tilde{\nu} (\upsilon+\dfrac{1}{2}) + \tilde{B}_{\upsilon} J (J+1) \label{combo1}\]

However, this approximation ignores the fact that the rotational motions affect the centrifugal stretching of a bond, and thus the bond length and vibrational motions are afected by rotational motion. Vice versa, a vibrational excitation would increase the equilibrium bond length (\(r_e\)), and would affect the Moment of Inertia (\(I\)). A more complete representation of the energies of roto-vibrational states is expressed as a term value, \(T(v, J)\), is given below. \(T(v,J)\) in Equation \ref{combo2} combines factors from rotational (rigid rotor) and vibrational (harmonic oscillator) energies, as well as factors that account for anharmonicity, centrifugal stretching, and the interactions between rotational and vibrational motions.

\[T(\upsilon, J)=\frac{E(\upsilon, J)}{h c}=\tilde{\nu}_e\left(\upsilon+\frac{1}{2}\right)-\tilde{\nu}_e x_e\left(\upsilon+\frac{1}{2}\right)^2+B_e J(J+1) -D_e J^2(J+1)^2-\alpha_e\left(\upsilon+\frac{1}{2}\right) J(J+1) \label{combo2}\]

where \(c\) is the speed of light, \(\tilde{\nu}\) is the frequency in cm-1, \(\upsilon\) is the vibrational quantum number, \(J\) is the rotational quantum number, and \(r_e\) is the internuclear separation. This expression takes into account the following:

• Anharmonicity with the term \(-\tilde{\nu} x_e\left(v+\frac{1}{2}\right)^2\), where \(\tilde{\nu} x\) is the anharmonicity parameter in \(cm^{-1}\).
• Centrifugal stretching with the term \(-D J^2(J+1)^2\), where \(D\) is a constant.
• The interaction between rotational and vibrational motions with the term \(-\alpha\left(\upsilon+\frac{1}{2}\right) J(J+1)\) where \(\alpha\) is the rotovibrational coupling constant that accounts for interactions between rotational and vibrational motions.

We can simply this through approximation of the harmonic oscillator by assuming that the the harmonic oscillator is good enough for the case where the vibrational transitions are occurring almost exclusively between the two lowest-energy vibrational states: \(\upsilon"=0\) and \(\upsilon'=1\). This gives a reasonable approximation that we can use as a model for rotational and vibrational motions of a diatomic:

Approximate allowed energies of roto-vibrational states:

\[\tilde{E}_{\upsilon, J}=\tilde{\nu}\left(\upsilon+\frac{1}{2}\right)+\tilde{B} J(J+1) - \tilde{D} [J(J+1)]^2-\tilde{\alpha}\left(\upsilon+\frac{1}{2}\right) J(J+1)\] 

• \(\tilde{E}\) is the energy 
• \(\tilde{\nu}\) is the vibrational frequency in \(cm^{-1}\)
• \(\upsilon\) is the vibrational quantum number
• \(J\) is the rotational quantum number
• \(B\) is the rotational constant
• \(D\) is a constant related to centrifugal stretching
• \(\tilde{\alpha}\) is the rotovibrational coupling constant in \(cm^{-1}\)

 

Selection Rules for vibrational and rotational transitions on diatomic molecules

• Vibrational Transition Selection Rules: The vibrational quantum number can change by 1: \(\Delta \upsilon = \pm1\). However, normally we can assume energy can only go upwards because of the nearly homogeneous population of \(\upsilon"=0\) near room temperature.
• Rotational Transition Selection Rules: The rotational quantum number can change by 1: \(\Delta J = \pm1\). Since at room temperature, \(J" =0,1,2...\) (several different rotational states are populated), transitions to higher and lower-energy rotational states are possible.

The P, Q, and R Branches

These selection rules mean that transitions with \(\Delta J\) or \(\Delta \upsilon\) equal to 0, 2, 3...etc are not allowed. The fact that the transition \(\Delta J = 0\) is forbidden means that a purely vibrational excitation (with no accompanying rotational transition) is not observed in the case of diatomic molecules. The rotational selection rule gives rise to distinct "branches" of the gas phase IR spectrum for diatomics like HCl; They are named using letters P, Q, R in order of increasing energy and corresponding to \(\Delta J = -1,0,+1\), respectively. Due to the unequal spacing of rotational energy levels, each transition requires a different energy.

At the highest energies are the transitions of the R-branch (when \(\Delta J=+1\)) and at the lowest energies are the transitions of the P-branch (\(\Delta J = -1\)). Between the P and R branches is the Q branch (\(\Delta J = 0\)). The Q branch is absent in the gas phase IR spectrum of HCl because \(\Delta J = 0\) is forbidden; thus it appears as a gap in the spectrum . Figure \(\PageIndex{4}\) illustrates allowed transitions on the energy diagram .

Figure \(\PageIndex{4}\): Allowed Rotation-Vibration Transitions are indicated using vertical arrows. The vibrational energy states are indicated with \(upsilon\) and rotational energy levels indicated by \(J\). A) The rotational energy levels (\(J\)) are superimposed on the vibrational energy levels of the ground state (\(\upsilon"\)) and first vibrational excited state (\(\upsilon '\)). B) Illustration of the relative energy for transitions of P and R branches. Because of unequal spacing between the rotational energy levels, the individual transitions differ in energy. In panel A, arrows increase in magnitude from left to right. To illustrate this, each arrow from panel A is placed with tails aligned in panel B so their relative magnitudes are obvious. The magnitude of the energy transition is qualitatively indicated by the length of the arrow. C) The P and R branches, the m values, and the arrows from Panels A and B are annotated on the FTIR spectrum of HCl (taken at 0.1 \(cm^{-1}\) resolution). (Kathryn Haas; CC-BY-SA)

Frequencies of P, Q, and R Branches

The frequency of a rotovibrational transition is the difference in energy (in \(cm^{-1}\)) of the excited state and ground state: \(T(\upsilon ', J') - T(\upsilon ", J") \). Thus the frequencies of vibrational transition from \(v = 0 \rightarrow 1\) can be calculated from the Equation \ref{combo2}. The calculation is simplified by dropping \(D_e\) out of the equation, since \(D_e\) (the centrifugal distortion constant) is usually very small. Simplified equations for calculations of the frequencies of each peak in the R and P branches are given below.

R Branch frequencies

For peaks of the R-branch, where allowed \(J\) values are \(J" = 0, 1, 2, ...\) and \(J'=1,2,3...\), and \(\Delta J = +1\), the vibrational frequency for a given \(J"\) is:

\[\tilde{\nu}_R=\tilde{\nu}_0+\left(2 B_e-3 \alpha_e\right)+\left(2 B_e-4 \alpha_e\right) J^{\prime \prime}-\alpha_e J^{\prime \prime 2} \label{vr}\]

Q Branch (the forbidden frequency)

\[\tilde{\nu}_0=\tilde{\nu_e}-2\tilde{\nu_e}x_e\]

*this is the forbidden transition (because \(\Delta J=0\) is forbidden). This is the frequency of the forbidden "vibration-only" transition, and it appears as a gap in the spectrum.

P Branch frequencies

For peaks of the P branch, where allowed \(J\) values are \(J" = 1, 2, 3, ...\) and \(J'=0,1,2...\), and \(\Delta J = -1\), the vibrational frequency for a given \(J"\) is:

\[\tilde{\nu}_P=\tilde{\nu}_0-\left(2 B_e-2 \alpha_e\right) J^{\prime \prime}-\alpha_e J^{\prime \prime 2}\label{vp}\]

General equation for all frequencies

We can write a more general equation for the frequencies by defining a new value \(m\), where \(m=J"+1\) for P branch, and \(m=J"-1\) for R branch:

\[\tilde{\nu}(m)=\tilde{\nu}_0+(2B_e-2\alpha_e)m-\alpha_em^2\]

Trends in peak spacing (\(\Delta \tilde{v}\))

Consider a scenario where the interactions between vibrational and rotational motions is negligible, and thus \(\alpha_e\) is small. In this scenario, the equations above (equations \ref{vr} and \ref{vp}) would yield a linearly relationship between \(J"\) and \(\tilde{\nu}\). In this imaginary scenario, we would expect a spectrum with equally-spaced lines in the P and R branches, where the separation between the lines is \(2B_e\) (in other words \(\Delta \tilde{\nu}=2B_e\)).

However, in a real diatomic like HCl, there is significant interaction between vibrational and rotational motions, and \(\alpha_e\) is significant. The result is a non-linear relationship between \(J'\) and \(\tilde{\nu}\), where the spacing of the R branch decreases as \(J"\) increases (R branch lines become more closely spaced), and the spacing in the P branch becomes larger as \(J"\) increases (P branch lines become are farther apart).

R Branch peaks become more closely spaced

A closer look at

\[\tilde{\nu}_R = \tilde{\nu}+2\tilde{B}_1+(3\tilde{B}_1-\tilde{B}_0)J+(\tilde{B}_1-\tilde{B}_0)J^2\]

shows that the last term in the parentheses \((\tilde{B}_1-\tilde{B}_0)\) will be always negative because \(\tilde{B}_1 < \tilde{B}_0\), and it also multiplies with \(J^2\), so the square term \((\tilde{B}_1-\tilde{B}_0)J^2\) will give a larger negative value for increasing \(J\). As a result, \(\tilde{\nu}_R=\tilde{\nu} + \)(smaller and smaller value) as J increase. Because the rotational frequencies keep getting smaller, the spacing between lines in R branch decreases as J increases.

Increasing in Spacing of Lines in the P Branch with Decreasing J

Using the same analysis as above,

\[\tilde{\nu}_P = \tilde{\nu}-(\tilde{B}_1+\tilde{B}_0)J+(\tilde{B}_1-\tilde{B}_0)J^2\]

shows that the last term in the parentheses \((\tilde{B}_1-\tilde{B}_0)\) will be always negative because \(\tilde{B}_1 < \tilde{B}_0\), and it also multiplies with \(J^2\), so the square term \((\tilde{B}_1-\tilde{B}_0)J^2\) will give a larger negative value even for decreasing \(J\). As a result, \(\tilde{\nu}_R=\tilde{\nu} - \)(smaller and smaller value) as J decreases. Because the rotational frequencies keep getting larger, the spacing between lines in P branch increase as J decreases.

References

1. McQuarrie, Donald A. Quantum Chemistry. New York: University Science Books, 2007.

Contributors and Attributions

• Dayton Dang
• Kathryn Haas