8.3: Quantifying Heat and Work

Learning Objectives

• Distinguish the related properties of heat, thermal energy, and temperature
• Define and distinguish specific heat and heat capacity, and describe the physical implications of both
• Perform calculations involving heat, specific heat, and temperature change
• Perform Calculation involving work.

Thermal Energy, Temperature, and Heat

Thermal energy is kinetic energy associated with the random motion of atoms and molecules. Temperature is a quantitative measure of “hot” or “cold.” When the atoms and molecules in an object are moving or vibrating quickly, they have a higher average kinetic energy (KE), and we say that the object is “hot.” When the atoms and molecules are moving slowly, they have lower KE, and we say that the object is “cold” (Figure \(\PageIndex{1}\)). Assuming that no chemical reaction or phase change (such as melting or vaporizing) occurs, increasing the amount of thermal energy in a sample of matter will cause its temperature to increase. And, assuming that no chemical reaction or phase change (such as condensation or freezing) occurs, decreasing the amount of thermal energy in a sample of matter will cause its temperature to decrease.

Figure \(\PageIndex{1}\): (a) The molecules in a sample of hot water move more rapidly than (b) those in a sample of cold water.

Interactive Element: PhET

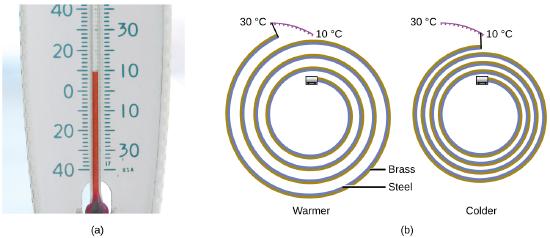
Most substances expand as their temperature increases and contract as their temperature decreases. This property can be used to measure temperature changes, as shown in Figure \(\PageIndex{2}\). The operation of many thermometers depends on the expansion and contraction of substances in response to temperature changes.

Figure \(\PageIndex{2}\): (a) In an alcohol or mercury thermometer, the liquid (dyed red for visibility) expands when heated and contracts when cooled, much more so than the glass tube that contains the liquid. (b) In a bimetallic thermometer, two different metals (such as brass and steel) form a two-layered strip. When heated or cooled, one of the metals (brass) expands or contracts more than the other metal (steel), causing the strip to coil or uncoil. Both types of thermometers have a calibrated scale that indicates the temperature. (credit a: modification of work by “dwstucke”/Flickr). (c) The demonstration allows one to view the effects of heating and cooling a coiled bimetallic strip.A bimetallic coil from a thermometer reacts to the heat from a lighter, by uncoiling and then coiling back up when the lighter is removed. Animation used with permission from Hustvedt (via Wikipedia).

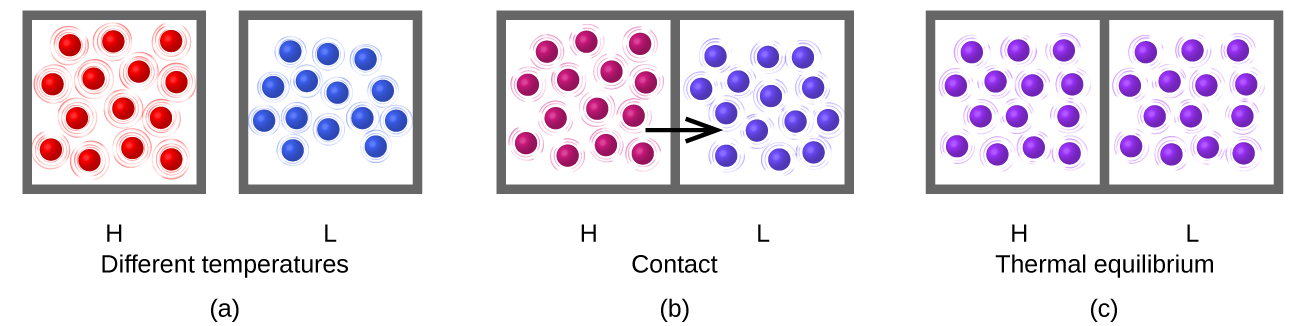
Heat (q) is the transfer of thermal energy between two bodies at different temperatures. Heat flow (a redundant term, but one commonly used) increases the thermal energy of one body and decreases the thermal energy of the other. Suppose we initially have a high temperature (and high thermal energy) substance (H) and a low temperature (and low thermal energy) substance (L). The atoms and molecules in H have a higher average KE than those in L. If we place substance H in contact with substance L, the thermal energy will flow spontaneously from substance H to substance L. The temperature of substance H will decrease, as will the average KE of its molecules; the temperature of substance L will increase, along with the average KE of its molecules. Heat flow will continue until the two substances are at the same temperature (Figure \(\PageIndex{3}\)).

Figure \(\PageIndex{3}\): (a) Substances H and L are initially at different temperatures, and their atoms have different average kinetic energies. (b) When they are put into contact with each other, collisions between the molecules result in the transfer of kinetic (thermal) energy from the hotter to the cooler matter. (c) The two objects reach “thermal equilibrium” when both substances are at the same temperature, and their molecules have the same average kinetic energy.

Matter undergoing chemical reactions and physical changes can release or absorb heat. A change that releases heat is called an exothermic process. For example, the combustion reaction that occurs when using an oxyacetylene torch is an exothermic process—this process also releases energy in the form of light as evidenced by the torch’s flame (Figure \(\PageIndex{4a}\)). A reaction or change that absorbs heat is an endothermic process. The cold pack shown in (Figure \(\PageIndex{4b}\))used to treat muscle strains provides an example of an endothermic process. When the substances in the cold pack (water and a salt like ammonium nitrate) are brought together, the resulting process absorbs heat, leading to the sensation of cold.

Figure \(\PageIndex{4}\): (a) An oxyacetylene torch produces heat by the combustion of acetylene in oxygen. The energy released by this exothermic reaction heats and then melts the metal being cut. The sparks are tiny bits of the molten metal flying away. (b) A cold pack uses an endothermic process to create the sensation of cold. (credit a: modification of work by “Skatebiker”/Wikimedia commons).

Measuring Heat and Heat Capacity

Historically, energy was measured in units of calories (cal). A calorie is the amount of energy required to raise one gram of water by 1 degree C (1 kelvin). However, this quantity depends on the atmospheric pressure and the starting temperature of the water. The ease of measurement of energy changes in calories has meant that the calorie is still frequently used. The Calorie (with a capital C), or large calorie, commonly used in quantifying food energy content, is a kilocalorie. The SI unit of heat, work, and energy is the joule. A joule (J) is defined as the amount of energy used when a force of 1 newton moves an object 1 meter. It is named in honor of the English physicist James Prescott Joule. One joule is equivalent to 1 kg m²/s², which is also called 1 newton–meter. A kilojoule (kJ) is 1000 joules. To standardize its definition, 1 calorie has been set to equal 4.184 joules.

We now introduce two concepts useful in describing heat flow and temperature change. The heat capacity (C) of a body of matter is the quantity of heat (q) it absorbs or releases when it experiences a temperature change (ΔT) of 1 degree Celsius (or equivalently, 1 kelvin)

\[C=\dfrac{q}{ΔT} \label{5.2.1}\]

Heat capacity is determined by both the type and amount of substance that absorbs or releases heat. It is therefore an extensive property—its value is proportional to the amount of the substance.

For example, consider the heat capacities of two cast iron frying pans. The heat capacity of the large pan is five times greater than that of the small pan because, although both are made of the same material, the mass of the large pan is five times greater than the mass of the small pan. More mass means more atoms are present in the larger pan, so it takes more energy to make all of those atoms vibrate faster. The heat capacity of the small cast iron frying pan is found by observing that it takes 18,150 J of energy to raise the temperature of the pan by 50.0 °C

\[C_{\text{small pan}}=\mathrm{\dfrac{18,140\; J}{50.0\; °C} =363\; J/°C} \label{5.2.2}\]

The larger cast iron frying pan, while made of the same substance, requires 90,700 J of energy to raise its temperature by 50.0 °C. The larger pan has a (proportionally) larger heat capacity because the larger amount of material requires a (proportionally) larger amount of energy to yield the same temperature change:

\[C_{\text{large pan}}=\mathrm{\dfrac{90,700\; J}{50.0\;°C}=1814\; J/°C} \label{5.2.3}\]

The specific heat capacity (c) of a substance, commonly called its “specific heat,” is the quantity of heat required to raise the temperature of 1 gram of a substance by 1 degree Celsius (or 1 kelvin):

\[c = \dfrac{q}{\mathrm{m\Delta T}} \label{5.2.4}\]

Specific heat capacity depends only on the kind of substance absorbing or releasing heat. It is an intensive property—the type, but not the amount, of the substance is all that matters. For example, the small cast iron frying pan has a mass of 808 g. The specific heat of iron (the material used to make the pan) is therefore:

\[c_\ce{iron}=\mathrm{\dfrac{18,140\; J}{(808\; g)(50.0\;°C)} = 0.449\; J/g\; °C} \label{5.2.5}\]

The large frying pan has a mass of 4040 g. Using the data for this pan, we can also calculate the specific heat of iron:

\[c_\ce{iron}=\mathrm{\dfrac{90,700\; J}{(4,040\; g)(50.0\;°C)}=0.449\; J/g\; °C} \label{5.2.6}\]

Although the large pan is more massive than the small pan, since both are made of the same material, they both yield the same value for specific heat (for the material of construction, iron). Note that specific heat is measured in units of energy per temperature per mass and is an intensive property, being derived from a ratio of two extensive properties (heat and mass). The molar heat capacity, also an intensive property, is the heat capacity per mole of a particular substance and has units of J/mol °C (Figure \(\PageIndex{5}\)).

Figure \(\PageIndex{5}\): Due to its larger mass, a large frying pan has a larger heat capacity than a small frying pan. Because they are made of the same material, both frying pans have the same specific heat. (credit: Mark Blaser).

Liquid water has a relatively high specific heat (about 4.2 J/g °C); most metals have much lower specific heats (usually less than 1 J/g °C). The specific heat of a substance varies somewhat with temperature. However, this variation is usually small enough that we will treat specific heat as constant over the range of temperatures that will be considered in this chapter. Specific heats of some common substances are listed in Table \(\PageIndex{1}\).

Table \(\PageIndex{1}\): Specific Heats of Common Substances at 25 °C and 1 bar

Substance	Symbol (state)	Specific Heat (J/g °C)
helium	He(g)	5.193
water	H2O(l)	4.184
ethanol	C2H6O(l)	2.376
ice	H2O(s)	2.093 (at −10 °C)
water vapor	H2O(g)	1.864
nitrogen	N2(g)	1.040
air		1.007
oxygen	O2(g)	0.918
aluminum	Al(s)	0.897
carbon dioxide	CO2(g)	0.853
argon	Ar(g)	0.522
iron	Fe(s)	0.449
copper	Cu(s)	0.385
lead	Pb(s)	0.130
gold	Au(s)	0.129
silicon	Si(s)	0.712

If we know the mass of a substance and its specific heat, we can determine the amount of heat, q, entering or leaving the substance by measuring the temperature change before and after the heat is gained or lost:

\[\begin{align*} q &= \ce{(specific\: heat)×(mass\: of\: substance)×(temperature\: change)}\label{5.2.7}\\q&=c×m×ΔT \\[4pt] &=c×m×(T_\ce{final}−T_\ce{initial})\end{align*}\]

In this equation, \(c\) is the specific heat of the substance, m is its mass, and ΔT (which is read “delta T”) is the temperature change, T_final − T_initial. If a substance gains thermal energy, its temperature increases, its final temperature is higher than its initial temperature, T_final − T_initial has a positive value, and the value of q is positive. If a substance loses thermal energy, its temperature decreases, the final temperature is lower than the initial temperature, T_final − T_initial has a negative value, and the value of q is negative.

Example \(\PageIndex{1}\): Measuring Heat

A flask containing \(\mathrm{8.0 \times 10^2\; g}\) of water is heated, and the temperature of the water increases from 21 °C to 85 °C. How much heat did the water absorb?

Solution

To answer this question, consider these factors:

• the specific heat of the substance being heated (in this case, water)
• the amount of substance being heated (in this case, 800 g)
• the magnitude of the temperature change (in this case, from 21 °C to 85 °C).

The specific heat of water is 4.184 J/g °C, so to heat 1 g of water by 1 °C requires 4.184 J. We note that since 4.184 J is required to heat 1 g of water by 1 °C, we will need 800 times as much to heat 800 g of water by 1 °C. Finally, we observe that since 4.184 J are required to heat 1 g of water by 1 °C, we will need 64 times as much to heat it by 64 °C (that is, from 21 °C to 85 °C).

This can be summarized using the equation:

\[\begin{align*} q&=c×m×ΔT \\[4pt] &=c×m×(T_\ce{final}−T_\ce{initial}) \\[4pt] &=\mathrm{(4.184\:J/\cancel{g}°C)×(800\:\cancel{g})×(85−21)°C}\\[4pt] &=\mathrm{(4.184\:J/\cancel{g}°\cancel{C})×(800\:\cancel{g})×(64)°\cancel{C}}\\[4pt] &=\mathrm{210,000\: J(=210\: kJ)} \end{align*}\]

Because the temperature increased, the water absorbed heat and \(q\) is positive.

Exercise \(\PageIndex{1}\)

How much heat, in joules, must be added to a \(\mathrm{5.00 \times 10^2 \;g}\) iron skillet to increase its temperature from 25 °C to 250 °C? The specific heat of iron is 0.451 J/g °C.

Answer

\(\mathrm{5.05 \times 10^4\; J}\)

Note that the relationship between heat, specific heat, mass, and temperature change can be used to determine any of these quantities (not just heat) if the other three are known or can be deduced.

Example \(\PageIndex{2}\): Determining Other Quantities

A piece of unknown metal weighs 348 g. When the metal piece absorbs 6.64 kJ of heat, its temperature increases from 22.4 °C to 43.6 °C. Determine the specific heat of this metal (which might provide a clue to its identity).

Solution

Since mass, heat, and temperature change are known for this metal, we can determine its specific heat using the relationship:

\[\begin{align*} q&=c \times m \times \Delta T \\[4pt] &=c \times m \times (T_\ce{final}−T_\ce{initial}) \end{align*}\]

Substituting the known values:

\[6,640\; \ce J=c \times \mathrm{(348\; g) \times (43.6 − 22.4)\; °C} \nonumber\]

Solving:

\[c=\mathrm{\dfrac{6,640\; J}{(348\; g) \times (21.2°C)} =0.900\; J/g\; °C} \nonumber\]

Comparing this value with the values in Table \(\PageIndex{1}\), this value matches the specific heat of aluminum, which suggests that the unknown metal may be aluminum.

Exercise \(\PageIndex{2}\)

A piece of unknown metal weighs 217 g. When the metal piece absorbs 1.43 kJ of heat, its temperature increases from 24.5 °C to 39.1 °C. Determine the specific heat of this metal, and predict its identity.



Answer

\(c = \mathrm{0.45 \;J/g \;°C}\); the metal is likely to be iron from checking Table \(\PageIndex{1}\).

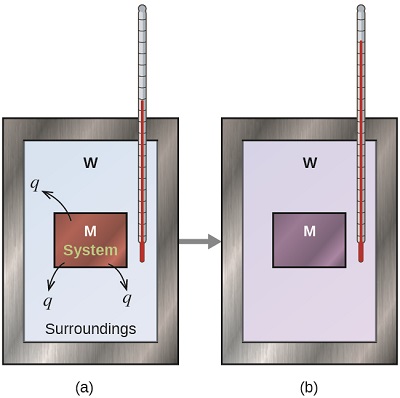
Heat exchange between a hot and a cold object

If we place the metal in the water, heat will flow from M to W. The temperature of M will decrease, and the temperature of W will increase, until the two substances have the same temperature—that is, when they reach thermal equilibrium (Figure \(\PageIndex{6}\)). If this occurs in a calorimeter, ideally all of this heat transfer occurs between the two substances assuming no heat is lost to the surroundings. Under these ideal circumstances, the net heat change is zero:

\[q_\mathrm{\,substance\: M} + q_\mathrm{\,substance\: W}=0 \label{5.3.1}\]

This relationship can be rearranged to show that the heat gained by substance M is equal to the heat lost by substance W:

\[q_\mathrm{\,substance\: M}=-q_\mathrm{\,substance\: W} \label{5.3.2}\]

The magnitude of the heat (change) is therefore the same for both substances, and the negative sign merely shows that \(q_{substance\, M}\) and \(q_{substance\, W}\) are opposite in direction of heat flow (gain or loss) but does not indicate the arithmetic sign of either q value (that is determined by whether the matter in question gains or loses heat, per definition). In the specific situation described, \(q_{substance\, M}\) is a negative value and \(q_{substance\, W}\) is positive, since heat is transferred from M to W.

Figure \(\PageIndex{6}\): In a simple calorimetry process, (a) heat, q, is transferred from the hot metal, M, to the cool water, W, until (b) both are at the same temperature.

Example \(\PageIndex{1}\): Heat Transfer between Substances at Different Temperatures

A hot 360-g piece of rebar (a steel rod used for reinforcing concrete) is dropped into 425 mL of water at 24.0 °C. The final temperature of the water is measured as 42.7 °C. Calculate the initial temperature of the piece of rebar. Assume the specific heat of steel is approximately the same as that for iron (Table T4), and that all heat transfer occurs between the rebar and the water (there is no heat exchange with the surroundings).

Solution

The temperature of the water increases from 24.0 °C to 42.7 °C, so the water absorbs heat. That heat came from the piece of rebar, which initially was at a higher temperature. Assuming that all heat transfer was between the rebar and the water, with no heat “lost” to the surroundings, then heat given off by rebar = − heat taken in by water, or:

\[q_\ce{rebar}=−q_\ce{water} \nonumber \]

Since we know how heat is related to other measurable quantities, we have:

\[(c×m×ΔT)_\ce{rebar}=−(c×m×ΔT)_\ce{water} \nonumber \]

Letting f = final and i = initial, in expanded form, this becomes:

\[ c_\ce{rebar}×m_\ce{rebar}×(T_\mathrm{f,rebar}−T_\mathrm{i,rebar})=−c_\ce{water}×m_\ce{water}×(T_\mathrm{f,water}−T_\mathrm{i,water}) \nonumber\]

The density of water is 1.0 g/mL, so 425 mL of water = 425 g. Noting that the final temperature of both the rebar and water is 42.7 °C, substituting known values yields:

\[ \mathrm{(0.449\:J/g\: °C)(360g)(42.7°C−\mathit T_\mathrm{i,rebar})=-(4.184\:J/g\: °C)(425\:g)(42.7°C−24.0°C)} \nonumber\]

\[\mathrm{\mathit T_{i,rebar}=\dfrac{(4.184\:J/g\: °C)(425\:g)(42.7°C−24.0°C)}{(0.449\:J/g\: °C)(360\:g)}+42.7°C} \nonumber\]

Solving this gives Ti,rebar= 248 °C, so the initial temperature of the rebar was 248 °C.

Exercise \(\PageIndex{1A}\)

A 248-g piece of copper is dropped into 390 mL of water at 22.6 °C. The final temperature of the water was measured as 39.9 °C. Calculate the initial temperature of the piece of copper. Assume that all heat transfer occurs between the copper and the water.

Answer

The initial temperature of the copper was 335.6 °C.

Exercise \(\PageIndex{1B}\)

A 248-g piece of copper initially at 314 °C is dropped into 390 mL of water initially at 22.6 °C. Assuming that all heat transfer occurs between the copper and the water, calculate the final temperature.

Answer

The final temperature (reached by both copper and water) is 38.7 °C.

This method can also be used to determine other quantities, such as the specific heat of an unknown metal.

Example \(\PageIndex{2}\): Identifying a Metal by Measuring Specific Heat

A 59.7 g piece of metal that had been submerged in boiling water was quickly transferred into 60.0 mL of water initially at 22.0 °C. The final temperature is 28.5 °C. Use these data to determine the specific heat of the metal. Use this result to identify the metal.

Solution

Assuming perfect heat transfer, heat given off by metal = −heat taken in by water, or:

\[q_\ce{metal}=−q_\ce{water} \nonumber\]

In expanded form, this is:

\[c_\ce{metal}×m_\ce{metal}×(T_\mathrm{f,metal}−T_\mathrm{i, metal})=−c_\ce{water}×m_\ce{water}×(T_\mathrm{f,water}−T_\mathrm{i,water}) \nonumber\]

Noting that since the metal was submerged in boiling water, its initial temperature was 100.0 °C; and that for water, 60.0 mL = 60.0 g; we have:

\[\mathrm{(\mathit c_{metal})(59.7\:g)(28.5°C−100.0°C)=−(4.18\:J/g\: °C)(60.0\:g)(28.5°C−22.0°C)} \nonumber\]

Solving this:

\[\mathrm{\mathit c_{metal}=\dfrac{−(4.184\:J/g\: °C)(60.0\:g)(6.5°C)}{(59.7\:g)(−71.5°C)}=0.38\:J/g\: °C} \nonumber\]

Comparing this with values in Table T4, our experimental specific heat is closest to the value for copper (0.39 J/g °C), so we identify the metal as copper.

Exercise \(\PageIndex{2}\)

A 92.9-g piece of a silver/gray metal is heated to 178.0 °C, and then quickly transferred into 75.0 mL of water initially at 24.0 °C. After 5 minutes, both the metal and the water have reached the same temperature: 29.7 °C. Determine the specific heat and the identity of the metal. (Note: You should find that the specific heat is close to that of two different metals. Explain how you can confidently determine the identity of the metal).

Answer

\(c_{metal}= 0.13 \;J/g\; °C\)

This specific heat is close to that of either gold or lead. It would be difficult to determine which metal this was based solely on the numerical values. However, the observation that the metal is silver/gray in addition to the value for the specific heat indicates that the metal is lead.

Conservation of Energy: The Movement of Heat between Substances: https://youtu.be/pGEYy-pNHBg

Mechanical Work

One definition of energy is the capacity to do work. There are many kinds of work, including mechanical work, electrical work, and work against a gravitational or a magnetic field. Here we will consider only mechanical work and focus on the work done during changes in the pressure or the volume of a gas.

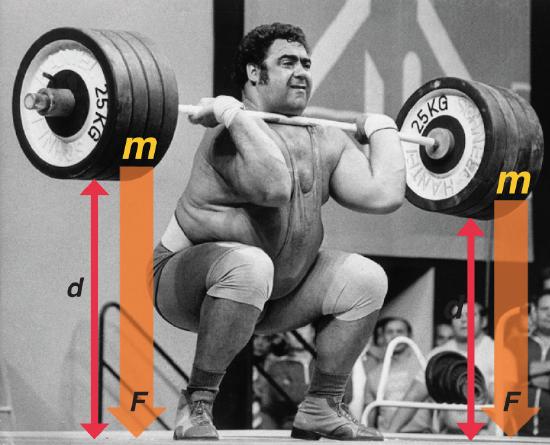
The easiest form of work to visualize is mechanical work (Figure \(\PageIndex{7}\)), which is the energy required to move an object a distance \(d\) when opposed by a force \(F\), such as gravity:

\[w=F\,d \label{12.3.1}\]

with \(w\) is work, \(F\) is opposing force, and \(d\) is distance.

Figure \(\PageIndex{7}\): One form of energy is mechanical work, the energy required to move an object of mass \(m\) through distance \(d\) when opposed by a force \(F\), i.e., as gravity.

Because the force (\(F\)) that opposes the action is equal to the mass (\(m\)) of the object times its acceleration (\(a\)), Equation \(\ref{12.3.1}\) can be rewritten to:

\[w = m\,a\,d \label{12.3.2}\]

with \(w\) is work, \(m\) is mass, \(a\) is acceleration, and \(d\) is distance.

Recall from that weight is a force caused by the gravitational attraction between two masses, such as you and Earth. Hence for works against gravity (on Earth), \(a\) can be set to \(g=9.8\; m/s^2)\). Consider the mechanical work required for you to travel from the first floor of a building to the second. Whether you take an elevator or an escalator, trudge upstairs, or leap up the stairs two at a time, energy is expended to overcome the opposing force of gravity. The amount of work done (w) and thus the energy required depends on three things:

1. the height of the second floor (the distance \(d\));
2. your mass, which must be raised that distance against the downward acceleration due to gravity; and
3. your path.

Pressure-Volume (PV) Work

To describe this pressure–volume work (PV work), we will use such imaginary oddities as frictionless pistons, which involve no component of resistance, and ideal gases, which have no attractive or repulsive interactions. Imagine, for example, an ideal gas, confined by a frictionless piston, with internal pressure \(P_{int}\) and initial volume \(V_i\) (Figure \(\PageIndex{8}\)). If \(P_{ext} = P_{int}\), the system is at equilibrium; the piston does not move, and no work is done. If the external pressure on the piston (\(P_{ext}\)) is less than \(P_{int}\), however, then the ideal gas inside the piston will expand, forcing the piston to perform work on its surroundings; that is, the final volume (\(V_f\)) will be greater than \(V_i\). If \(P_{ext} > P_{int}\), then the gas will be compressed, and the surroundings will perform work on the system.

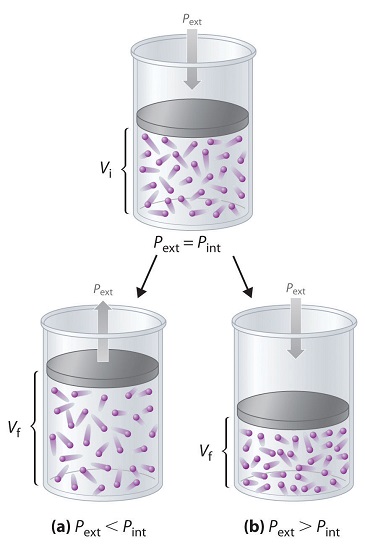
Figure \(\PageIndex{8}\): PV Work demonstrated with a frictionless piston. (a) if the external pressure is less than \(P_{int}\), the ideal gas inside the piston will expand, forcing the piston to perform work on its surroundings. The final volume (\(V_f\)) will be greater than \(V_i\). (b) Alternatively, if the external pressure is greater than \(P_{int}\), the gas will be compressed, and the surroundings will perform work on the system.

If the piston has cross-sectional area \(A\), the external pressure exerted by the piston is, by definition, the force per unit area:

\[P_{ext} = \dfrac{F}{A} \label{eq5}\]

The volume of any three-dimensional object with parallel sides (such as a cylinder) is the cross-sectional area times the height (\(V = Ah\)). Rearranging Equation \ref{eq5} to give

\[F = P_{ext}A\]

and defining the distance the piston moves (\(d\)) as \(Δh\), we can calculate the magnitude of the work performed by the piston by substituting into Equation \(\ref{12.3.1}\):

\[w = F d = P_{ext}AΔh \label{12.3.3}\]

The change in the volume of the cylinder (\(ΔV\)) as the piston moves a distance d is \(ΔV = AΔh\), as shown in Figure \(\PageIndex{9}\).

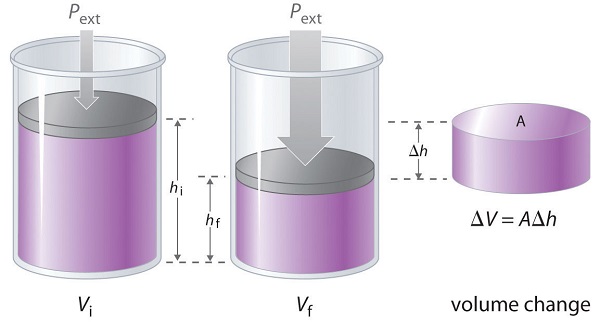
Figure \(\PageIndex{9}\): Work Performed with a change in volume. The change in the volume (\(ΔV\)) of the cylinder housing a piston is \(ΔV = AΔh\) as the piston moves. The work performed by the surroundings on the system as the piston moves inward is given by Equation \ref{12.3.4}.

The PV work performed is thus

\[ w = P_{ext}ΔV \label{12.3.4}\]

The units of work obtained using this definition are correct for energy: pressure is force per unit area (newton/m²) and volume has units of cubic meters, so

\[w=\left(\dfrac{F}{A}\right)_{\textrm{ext}}(\Delta V)=\dfrac{\textrm{newton}}{\textrm m^2}\times \textrm m^3=\mathrm{newton\cdot m}=\textrm{joule}\]

If we use atmospheres for P and liters for V, we obtain units of L·atm for work. These units correspond to units of energy, as shown in the different values of the ideal gas constant R:

\[R=\dfrac{0.08206\;\mathrm{L\cdot atm}}{\mathrm{mol\cdot K}}=\dfrac{8.314\textrm{ J}}{\mathrm{mol\cdot K}}\]

Thus 0.08206 L·atm = 8.314 J and 1 L·atm = 101.3 J.

Example\(\PageIndex{3}\)

1. How much work is done by a gas that expands from 2 liters to 5 liters against an external pressure of 750 mmHg?
2. How much work is done by 0.54 moles of a gas that has an initial volume of 8 liters and expands under the following conditions: 30 ^oC and 1.3 atm?
3. How much work is done by a gas (P=1.7 atm, V=1.56 L) that expands against an external pressure of 1.8 atm?

Solution a

\[w = − PΔV\]

\[ΔV = V_{final} - V_{Initial} = 5 \,L - 2\, L = 3 L\]

Convert 750 mmHg to atm:

\[750 mmHg * 1/760 (atm/mmHg) = 0.9868 atm.\]

\[W = − pΔV = -(.9868\, atm)(3\,L) = -2.96 \,L\, atm.\]

Solution b

First we must find the final volume using the ideal gas law:

\[pV = nRT\]

or

\[V = \dfrac{nRT}{P} = \dfrac{ [(0.54 \,moles)(0.082057 (L\, atm)/ (mol\, K))(303\,K)] }{1.3\, atm} = 10.33\, L\]

\[ΔV = V_{final} - V_{initial} = 10.3\, L - 8\, L = 2.3\, L\]

\[w = − pΔV = - (1.3\, atm)(2.3 \,L) = -3\, L\, atm.\]

Solution c

\[w = - p * ΔV\) = - (1.8 \,atm )\, ΔV.\]

Given \(p_1\), \(V_1\), and \(p_2\), find \(V_2\): \(p_1V_1=p_2V_2\) (at constant \(T\) and \(n\))

\(V_2= (V_1* P_1) / P_2\) = (1.56 L * 1.7 atm) / 1.8 atm = 1.47 L

Now,

\[ΔV = V_2 - V_1=1.47\, L - 1.56\, L = -0.09\]

\[w = - (1.8 atm) * (-0.09 L) = 0.162 L atm.\]

Whether work is defined as having a positive sign or a negative sign is a matter of convention. Heat flow is defined from a system to its surroundings as negative; using that same sign convention, we define work done by a system on its surroundings as having a negative sign because it results in a transfer of energy from a system to its surroundings. This is an arbitrary convention and one that is not universally used. Some engineering disciplines are more interested in the work done on the surroundings than in the work done by the system and therefore use the opposite convention. Because ΔV > 0 for an expansion, Equation \(\ref{12.3.4}\) must be written with a negative sign to describe PV work done by the system as negative:

\[ w = −P_{ext}ΔV \label{12.3.5}\]

The work done by a gas expanding against an external pressure is therefore negative, corresponding to work done by a system on its surroundings. Conversely, when a gas is compressed by an external pressure, ΔV < 0 and the work is positive because work is being done on a system by its surroundings.

A Matter of Convention

• Heat flow is defined from the system to its surroundings as negative
• Work is defined as by the system on its surroundings as negative

Suppose, for example, that the system under study is a mass of steam heated by the combustion of several hundred pounds of coal and enclosed within a cylinder housing a piston attached to the crankshaft of a large steam engine. The gas is not ideal, and the cylinder is not frictionless. Nonetheless, as steam enters the engine chamber and the expanding gas pushes against the piston, the piston moves, so useful work is performed. In fact, PV work launched the Industrial Revolution of the 19th century and powers the internal combustion engine on which most of us still rely for transportation.

Figure \(\PageIndex{10}\): Work Is Not a State Function. In pathway A, the volume of a gas is initially increased while its pressure stays constant (step 1). Its pressure is then decreased while the volume remains constant (step 2). Pathway B reverses these steps. Although (\(V_1\), \(P_1\)) and (\(V_2\), \(P_2\)) are identical in both cases, the amount of work done (shaded area) depends on the pathway taken.

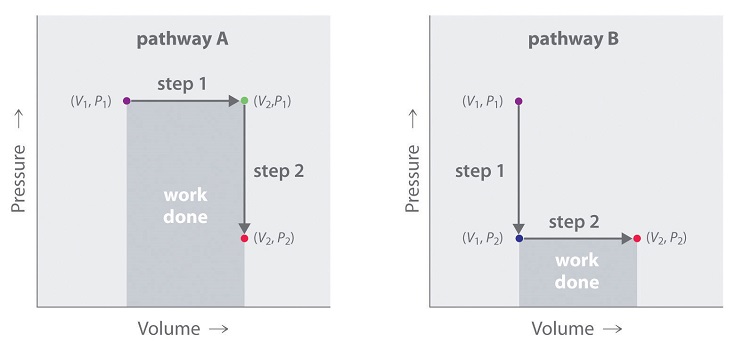
In contrast to internal energy, work is not a state function. We can see this by examining Figure \(\PageIndex{10}\), in which two different, two-step pathways take a gaseous system from an initial state to a final state with corresponding changes in temperature. In pathway A, the volume of a gas is initially increased while its pressure stays constant (step 1); then its pressure is decreased while the volume remains constant (step 2). In pathway B, the order of the steps is reversed. The temperatures, pressures, and volumes of the initial and final states are identical in both cases, but the amount of work done, indicated by the shaded areas in the figure, is substantially different. As we can see, the amount of work done depends on the pathway taken from (\(V_1\), \(P_1\)) to (\(V_2\), \(P_2\)), which means that work is not a state function.

Internal energy is a state function, whereas work is not.

Example \(\PageIndex{4}\)

A small high-performance internal combustion engine has six cylinders with a total nominal displacement (volume) of 2.40 L and a 10:1 compression ratio (meaning that the volume of each cylinder decreases by a factor of 10 when the piston compresses the air–gas mixture inside the cylinder prior to ignition). How much work in joules is done when a gas in one cylinder of the engine expands at constant temperature against an opposing pressure of 40.0 atm during the engine cycle? Assume that the gas is ideal, the piston is frictionless, and no energy is lost as heat.

Given: final volume, compression ratio, and external pressure

Asked for: work done

Strategy:

Calculate the final volume of gas in a single cylinder. Then compute the initial volume of gas in a single cylinder from the compression ratio. Use Equation \(\ref{12.3.5}\) to calculate the work done in liter-atmospheres. Convert from liter-atmospheres to joules.

Solution:

A To calculate the work done, we need to know the initial and final volumes. The final volume is the volume of one of the six cylinders with the piston all the way down: V_f = 2.40 L/6 = 0.400 L. With a 10:1 compression ratio, the volume of the same cylinder with the piston all the way up is V_i = 0.400 L/10 = 0.0400 L. Work is done by the system on its surroundings, so work is negative.

\[\begin{align} w &= −P_{ext}ΔV \nonumber \\[4pt] &= −(40.0\, atm)(0.400\, L − 0.0400 \,L) \nonumber \\[4pt] &= −14.4\, L·atm \nonumber \end{align} \nonumber\]

Converting from liter-atmospheres to joules,

\[\begin{align} w &=-(14.4\;\mathrm{L\cdot atm})[101.3\;\mathrm{J/(L\cdot atm)}] \nonumber \\[4pt] &= -1.46\times10^3\textrm{ J} \nonumber \end{align} \nonumber\]

In the following exercise, you will see that the concept of work is not confined to engines and pistons. It is found in other applications as well.

Exercise \(\PageIndex{3}\)

Breathing requires work, even if you are unaware of it. The lung volume of a 70 kg man at rest changed from 2200 mL to 2700 mL when he inhaled, while his lungs maintained a pressure of approximately 1.0 atm. How much work in liter-atmospheres and joules was required to take a single breath? During exercise, his lung volume changed from 2200 mL to 5200 mL on each in-breath. How much additional work in joules did he require to take a breath while exercising?

Answer

−0.500 L·atm, or −50.7 J; −304 J; if he takes a breath every three seconds, this corresponds to 1.4 Calories per minute (1.4 kcal).

Work and Chemical Reactions

We have stated that the change in energy (\(ΔU\)) is equal to the sum of the heat produced and the work performed. Work done by an expanding gas is called pressure-volume work, (or just PV work). Consider, for example, a reaction that produces a gas, such as dissolving a piece of copper in concentrated nitric acid. The chemical equation for this reaction is as follows:

\[Cu_{(s)} + 4HNO_{3(aq)} \rightarrow Cu(NO_3)_{2(aq)} + 2H_2O_{(l)} + 2NO_{2(g)} \label{12.3.5a}\]

If the reaction is carried out in a closed system that is maintained at constant pressure by a movable piston, the piston will rise as nitrogen dioxide gas is formed (Figure \(\PageIndex{11}\)). The system is performing work by lifting the piston against the downward force exerted by the atmosphere (i.e., atmospheric pressure). We find the amount of PV work done by multiplying the external pressure P by the change in volume caused by movement of the piston (ΔV). At a constant external pressure (here, atmospheric pressure)

\[w = −PΔV \label{12.3.6}\]

The negative sign associated with \(PV\) work done indicates that the system loses energy. If the volume increases at constant pressure (ΔV > 0), the work done by the system is negative, indicating that a system has lost energy by performing work on its surroundings. Conversely, if the volume decreases (ΔV < 0), the work done by the system is positive, which means that the surroundings have performed work on the system, thereby increasing its energy.

Figure \(\PageIndex{11}\): An Example of Work Performed by a Reaction Carried Out at Constant Pressure. (a) Initially, the system (a copper penny and concentrated nitric acid) is at atmospheric pressure. (b) When the penny is added to the nitric acid, the volume of \(\ce{NO2}\) gas that is formed causes the piston to move upward to maintain the system at atmospheric pressure. In doing so, the system is performing work on its surroundings.

The symbol \(U\) represents the internal energy of a system, which is the sum of the kinetic energy and potential energy of all its components. It is the change in internal energy that produces heat plus work. To measure the energy changes that occur in chemical reactions, chemists usually use a related thermodynamic quantity called enthalpy (H) (from the Greek enthalpein, meaning “to warm”). The enthalpy of a system is defined as the sum of its internal energy \(U\) plus the product of its pressure \(P\) and volume \(V\):

\[H =U + PV \label{12.3.7}\]

Because internal energy, pressure, and volume are all state functions, enthalpy is also a state function.

If a chemical change occurs at constant pressure (i.e., for a given P, ΔP = 0), the change in enthalpy (ΔH) is

\[ ΔH = Δ(U + PV) = ΔU + ΔPV = ΔU + PΔV \label{12.3.8}\]

Substituting \(q + w\) for \(ΔU\) (Equation \(\ref{12.3.8}\)) and \(−w\) for \(PΔV\) (Equation \(\ref{12.3.6}\)), we obtain

\[ΔH = ΔU + PΔV = q_p + w − w = q_p \label{12.3.9}\]

The subscript \(p\) is used here to emphasize that this equation is true only for a process that occurs at constant pressure. From Equation \(\ref{12.3.9}\) we see that at constant pressure the change in enthalpy, \(ΔH\) of the system, defined as \(H_{final} − H_{initial}\), is equal to the heat gained or lost.

\[ΔH = H_{final} − H_{initial} = q_p \label{12.3.10}\]

Just as with \(ΔU\), because enthalpy is a state function, the magnitude of \(ΔH\) depends on only the initial and final states of the system, not on the path taken. Most important, the enthalpy change is the same even if the process does not occur at constant pressure.

To find \(ΔH\) for a reaction, measure \(q_p\) under constant pressure.

Summary

Energy is the capacity to do work (applying a force to move matter). Kinetic energy (KE) is the energy of motion; potential energy is energy due to relative position, composition, or condition. When energy is converted from one form into another, energy is neither created nor destroyed (law of conservation of energy or first law of thermodynamics). Matter has thermal energy due to the KE of its molecules and temperature that corresponds to the average KE of its molecules. Heat is energy that is transferred between objects at different temperatures; it flows from a high to a low temperature. Chemical and physical processes can absorb heat (endothermic) or release heat (exothermic). The SI unit of energy, heat, and work is the joule (J). Specific heat and heat capacity are measures of the energy needed to change the temperature of a substance or object. The amount of heat absorbed or released by a substance depends directly on the type of substance, its mass, and the temperature change it undergoes.

Key Equations

• \(q=c×m×ΔT=c×m×(T_\ce{final}−T_\ce{initial})\)

Glossary

calorie (cal)

unit of heat or other energy; the amount of energy required to raise 1 gram of water by 1 degree Celsius; 1 cal is defined as 4.184 J

endothermic process

chemical reaction or physical change that absorbs heat

energy

capacity to supply heat or do work

exothermic process

chemical reaction or physical change that releases heat

heat (q)

transfer of thermal energy between two bodies

heat capacity (C)

extensive property of a body of matter that represents the quantity of heat required to increase its temperature by 1 degree Celsius (or 1 kelvin)

joule (J)

SI unit of energy; 1 joule is the kinetic energy of an object with a mass of 2 kilograms moving with a velocity of 1 meter per second, 1 J = 1 kg m²/s and 4.184 J = 1 cal

kinetic energy

energy of a moving body, in joules, equal to \(\dfrac{1}{2}mv^2\) (where m = mass and v = velocity)

potential energy

energy of a particle or system of particles derived from relative position, composition, or condition

specific heat capacity (c)

intensive property of a substance that represents the quantity of heat required to raise the temperature of 1 gram of the substance by 1 degree Celsius (or 1 kelvin)

temperature

intensive property of matter that is a quantitative measure of “hotness” and “coldness”

thermal energy

kinetic energy associated with the random motion of atoms and molecules

thermochemistry

study of measuring the amount of heat absorbed or released during a chemical reaction or a physical change

Outside Links

Gasparro, Frances P. "Remembering the sign conventions for q and w in deltaU = q - w." J. Chem. Educ. 1976: 53, 389. Koubek, E. "PV work demonstration (TD)." J. Chem. Educ. 1980: 57, 374. '

Contributors and Attributions

work (w)

energy transfer due to changes in external, macroscopic variables such as pressure and volume; or causing matter to move against an opposing force

Paul Flowers (University of North Carolina - Pembroke), Klaus Theopold (University of Delaware) and Richard Langley (Stephen F. Austin State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at http://cnx.org/contents/85abf193-2bd...a7ac8df6@9.110).