8.6: How Much of the Excess Reactant Remains after a Reaction

Last updated
Save as PDF

Page ID: 371650

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)

Learning Objectives

Identify the excess reactant in a given chemical reaction.
Calculate how much excess reactant(s) remains when the reaction is complete.

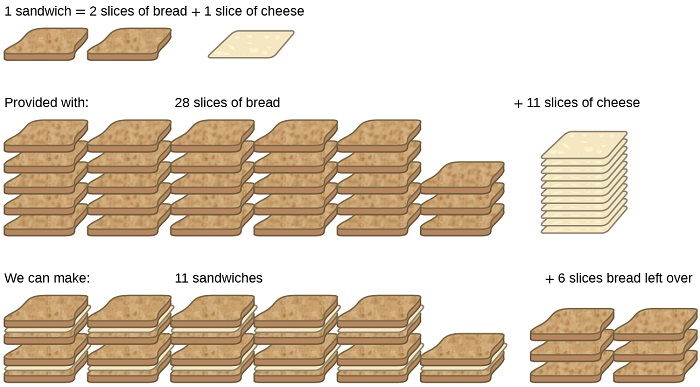
Consider the food analogy, making grilled cheese sandwiches (Figure \(\PageIndex{1}\)):

\[\text{1 slice of cheese} + \text{2 slices of bread} \rightarrow \text{1 sandwich} \label{4.5.A}\]

Stoichiometric amounts of sandwich ingredients for this recipe are bread and cheese slices in a 2:1 ratio. Provided with 28 slices of bread and 11 slices of cheese, one may prepare 11 sandwiches per the provided recipe, using all the provided cheese and having six slices of bread left over. In this scenario, the number of sandwiches prepared has been limited by the number of cheese slices, and six bread slices have been provided in excess.

This figure has three rows showing the ingredients needed to make a sandwich. The first row reads, “1 sandwich = 2 slices of bread + 1 slice of cheese.” Two slices of bread and one slice of cheese are shown. The second row reads, “Provided with: 28 slices of bread + 11 slices of cheese.” There are 28 slices of bread and 11 slices of cheese shown. The third row reads, “We can make: 11 sandwiches + 6 slices of bread left over.” 11 sandwiches are shown with six extra slices of bread. — Figure \(\PageIndex{1}\): Sandwich making can illustrate the concepts of limiting and excess reactants.

Consider this concept now with regard to a chemical process, the reaction of hydrogen with chlorine to yield hydrogen chloride:

\[\ce{H2}(g) + \ce{Cl2}(g)\rightarrow \ce{2HCl}(g)\]

The balanced equation shows the hydrogen and chlorine react in a 1:1 stoichiometric ratio. If these reactants are provided in any other amounts, one of the reactants will nearly always be entirely consumed, thus limiting the amount of product that may be generated. This substance is the limiting reactant, and the other substance is the excess reactant. Identifying the limiting and excess reactants for a given situation requires computing the molar amounts of each reactant provided and comparing them to the stoichiometric amounts represented in the balanced chemical equation.

For example, imagine combining 6 moles of H₂ and 4 moles of Cl₂. Identifying the limiting reactant involves comparing the amount of product expected for the complete reaction of each reactant. Each reactant amount is used to separately calculate the amount of product that would be formed per the reaction’s stoichiometry. The reactant yielding the lesser amount of product is the limiting reactant.

For the example in the previous paragraph, the complete reaction of the hydrogen would yield

\[\mathrm{mol\: HCl\: produced=6\: mol\:H_2\times \dfrac{2\: mol\: HCl}{1\: mol\:H_2}=12\: mol\: HCl}\]

The complete reaction of the provided chlorine would produce

\[\mathrm{mol\: HCl\: produced=4\: mol\:Cl_2\times \dfrac{2\: mol\: HCl}{1\: mol\:Cl_2}=8\: mol\: HCl}\]

The chlorine will be completely consumed once 8 moles of HCl have been produced. Since enough hydrogen was provided to yield 12 moles of HCl, there will be non-reacted hydrogen remaining once this reaction is complete. Chlorine, therefore, is the limiting reactant and hydrogen is the excess reactant (Figure \(\PageIndex{2}\)). To determine the amount of excess reactant that remains, the amount of hydrogen consumed in the reaction can be subtracted from the initial quantity of hydrogen.

The amount of hydrogen consumed is

\[\mathrm{mol\: H_2\: produced=8\: mol\:HCl\times \dfrac{1\: mol\: H_2}{2\: mol\:HCl}=4\: mol\: H_2}\]

Subtract the hydrogen consumed from the starting quantity

\[\mathrm{mole\: of\: excess\:H_{2}=6\:mol\:H_{2}\:initial\:-\:4\:mol\:H_{2}\:consumed\:=\:2\:mol\:H_{2}\; excess}\]

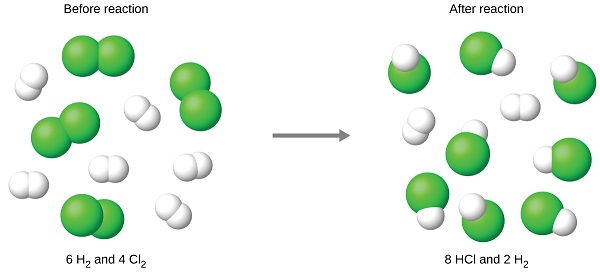
The figure shows a space-filling molecular models reacting. There is a reaction arrow pointing to the right in the middle. To the left of the reaction arrow there are three molecules each consisting of two green spheres bonded together. There are also five molecules each consisting of two smaller, white spheres bonded together. Above these molecules is the label, “Before reaction,” and below these molecules is the label, “6 H subscript 2 and 4 C l subscript 2.” To the right of the reaction arrow, there are eight molecules each consisting of one green sphere bonded to a smaller white sphere. There are also two molecules each consisting of two white spheres bonded together. Above these molecules is the label, “After reaction,” and below these molecules is the label, “8 H C l and 2 H subscript 2.” — Figure \(\PageIndex{2}\): When H₂ and Cl₂ are combined in nonstoichiometric amounts, one of these reactants will limit the amount of HCl that can be produced. This illustration shows a reaction in which hydrogen is present in excess and chlorine is the limiting reactant.

Example \(\PageIndex{3}\): Limiting Reactant and Mass of Excess Reactant

5.00 g Rb are combined with 3.44 g MgCl₂ according to the chemical reaction:

2 Rb (s) + MgCl₂ (s) → Mg (s) + 2 RbCl (s)

What mass of Mg is formed?
What mass of which reactant is left over?

Solution

Steps for Problem Solving
Identify the "given" information and what the problem is asking you to "find."	Given: 5.00 g Rb reacted; 3.44 g MgCl₂ reacted Find: theoretical yield Mg; identify excess reactant and its mass
List other known quantities.	1 mol Rb = 85.47 g Rb 1 mol MgCl₂ = 95.21 g MgCl₂ 1 mol Mg = 24.31 g Mg 2 mol Rb: 1 mol Mg 1 mol MgCl₂: 1 mol Mg
Prepare concept maps using the proper conversion factor(s).	\({\color[rgb]{0.5, 0.0, 0.5}\boxed{\;\;\;\mathrm g\;\mathrm{Rb}\;\;\;}}\xrightarrow[{85.47\;\mathrm g\;\mathrm{Rb}}]{1\;\mathrm{mol}\;\mathrm{Rb}}{\color[rgb]{0.8, 0.0, 0.0}\boxed{\;\;\mathrm{mol}\;\mathrm{Rb}\;\;}}\xrightarrow[{2\;\mathrm{mol}\;\mathrm{Rb}}]{1\;\mathrm{mol}\;\mathrm{Mg}}{\color[rgb]{0.0, 0.0, 1.0}\boxed{\;\;\mathrm{mol}\;\mathrm{Mg}\;\;}}\xrightarrow[{1\;\mathrm{mol}\;\mathrm{Mg}}]{24.31\;\mathrm g\;\mathrm{Mg}}{\color[rgb]{0.0, 0.5, 0.0}\boxed{\;\;\;\mathrm g\;\mathrm{Mg}\;\;\;}}\) \({\color[rgb]{0.5, 0.0, 0.5}\boxed{\;\mathrm g\;{\mathrm{MgCl}}_2\;}}\xrightarrow[{95.21\;\mathrm g\;{\mathrm{MgCl}}_2}]{1\;\mathrm{mol}\;{\mathrm{MgCl}}_2}{\color[rgb]{0.8, 0.0, 0.0}\boxed{\mathrm{mol}\;{\mathrm{MgCl}}_2}}\xrightarrow[{2\;\mathrm{mol}\;{\mathrm{MgCl}}_2}]{1\;\mathrm{mol}\;\mathrm{Mg}}{\color[rgb]{0.0, 0.0, 1.0}\boxed{\;\;\mathrm{mol}\;\mathrm{Mg}\;\;}}\xrightarrow[{1\;\mathrm{mol}\;\mathrm{Mg}}]{24.31\;\mathrm g\;\mathrm{Mg}}{\color[rgb]{0.0, 0.5, 0.0}\boxed{\;\;\;\mathrm g\;\mathrm{Mg}\;\;\;}}\)
Calculate the theoretical yield. Select the smallest answer.	\(5.00\:\cancel{\mathrm g\;\mathrm{Rb}}\times\dfrac{1\;\cancel{\mathrm{mol}\;\mathrm{Rb}}}{85.47\:\cancel{\mathrm g\;\mathrm{Rb}}}\times\dfrac{1\;\cancel{\mathrm{mol}\;\mathrm{Mg}}}{2\:\cancel{\mathrm{mol}\;\mathrm{Rb}}}\times\dfrac{24.31\;\mathrm g\;\mathrm{Mg}}{1\;\cancel{\mathrm{mol}\;\mathrm{Mg}}}=\boxed{0.711\;\mathrm g\;\mathrm{Mg}}\) \(3.44\:\cancel{\mathrm g\;{\mathrm{MgCl}}_2}\times\dfrac{1\;\cancel{\mathrm{mol}\;{\mathrm{MgCl}}_2}}{95.21\:\cancel{\mathrm g\;{\mathrm{MgCl}}_2}}\times\dfrac{1\;\cancel{\mathrm{mol}\;\mathrm{Mg}}}{1\:\cancel{\mathrm{mol}\;{\mathrm{MgCl}}_2}}\times\dfrac{24.31\;\mathrm g\;\mathrm{Mg}}{1\;\cancel{\mathrm{mol}\;\mathrm{Mg}}}=\xcancel{0.878\;\mathrm g\;\mathrm{Mg}}\)
Identify the limiting reactant(s) and excess reactant(s).	The limiting reactant is Rb since it would yield the least amount of product (0.711 g Mg). The excess reactant is MgCl₂ since its complete reaction would have yielded up to 0.878 g Mg.
Calculate the mass of excess reactant that reacts.	Start with 0.711 g Mg, since it is the theoretical yield and the amount produced. \(0.711\:\cancel{\mathrm g\;\mathrm{Mg}}\times\dfrac{1\;\cancel{\mathrm{mol}\;\mathrm{Mg}}}{24.31\:\cancel{\mathrm g\;\mathrm{Mg}}}\times\dfrac{1\;\cancel{\mathrm{mol}\;{\mathrm{MgCl}}_2}}{1\;\cancel{\mathrm{mol}\;\mathrm{Mg}}}\times\dfrac{95.21\;\mathrm g\;{\mathrm{MgCl}}_2}{1\;\cancel{\mathrm{mol}\;{\mathrm{MgCl}}_2}}=\boxed{2.78\;\mathrm g\;{\mathrm{MgCl}}_2\;\mathrm{reacted}}\)
Calculate the mass of excess reactant that remains and think about the result.	We started with 3.44 g MgCl₂ and found that 2.78 g MgCl₂ reacted. This makes sense, since MgCl₂ is the excess reactant. Less should react than we started with. 3.44 g MgCl₂ initially – 2.78 g MgCl₂ reacted = 0.66 g MgCl₂ remain

Exercise \(\PageIndex{1}\)

Given the balanced chemical equation:

2 C₈H₁₈ + 25 O₂ → 16 CO₂ + 18 H₂O

If 24.5 moles of C₈H₁₈ are reacted with 245 moles of O₂, how many moles of CO₂ are produced assuming complete reaction?
How many moles of which reactant remain unconsumed?

Answer A: 157 mol CO₂ are produced.

Answer B: 4.9 mol C₈H₁₈ remain unconsumed.

Exercise \(\PageIndex{2}\)

Potassium superoxide, KO₂, is used in rebreathing gas masks to generate oxygen according to the equation below.

4 KO₂ (s) + 2 H₂O (l) → 4 KOH (s) + 3 O₂ (g)

What is the theoretical yield of oxygen, in units of grams, when 108 g of KO₂ reacts with 16.8 g of H₂O?
Which reactant is the limiting reactant?
Which reactant is present in excess?

Answer A: 36.5 g O₂ are produced.

Answer B: The limiting reactant is KO₂.

Answer C: H₂O is present in excess.

Video Topics

A variation of limiting reactant problems involves determining how much of the non-limiting reactant remains after a reaction. This is done by generating mole ratio conversion unit created by from reaction's stoichiometry. By determining how much of the non-limiting reactant is used during the reaction the amount of excess can be determined.

Link to Video

How Much of the Excess Reactant Remains after a Reaction: https://youtu.be/K2II-QuBsKs

This project was preformed to supply Libretext authors with videos on General Chemistry topics which can be used to enhance their projects. Also, these videos are meant to act as a learning resource for all General Chemistry students.

Attribution

Prof. Steven Farmer (Sonoma State University)
Sarick Shah (UCD)
Marisa Alviar-Agnew (Sacramento City College)
Henry Agnew (UC Davis)
Lance S. Lund (Anoka-Ramsey Community College)

Search

Text Color

Text Size

Margin Size

Font Type