2.4: Properties of Matter - Mass, Length, Volume and Temperature

Learning Objective

• Learn the units that go with various quantities
• Express units using their abbreviations
• Make new units by combining numerical prefixes with units

Mass vs. Weight

One of the many interesting things about travel in outer space is the idea of weightlessness. If something is not fastened down, it will float in mid-air. Early astronauts learned that weightlessness had bad effects on bone structure. If there was no pressure on the legs, those bones would begin to lose mass. Weight provided by gravity is needed to maintain healthy bones. Specially designed equipment is now a part of every space mission so the astronauts can maintain good body fitness.

Mass is a measure of the amount of matter that an object contains. The mass of an object is made in comparison to the standard mass of 1 kilogram. The kilogram was originally defined as the mass of \(1 \: \text{L}\) of liquid water at \(4^\text{o} \text{C}\) (volume of a liquid changes slightly with temperature).  Currently, the kilogram is defined as the equivalent mass of the energy of a photon given its frequency, via the Planck constant.  In the laboratory, mass is measured with a balance (see below), which must be calibrated with a standard mass so that its measurements are accurate.

Figure \(\PageIndex{1}\): An analytical balance makes very sensitive mass measurements in a laboratory, usually in grams.

Other common units of mass are the gram and the milligram. A gram is 1/1000th of a kilogram, meaning that there are \(1000 \: \text{g}\) in \(1 \: \text{kg}\). A milligram is 1/1000th of a gram, so there are \(1000 \: \text{mg}\) in \(1 \: \text{g}\).

The Difference Between Mass and Weight

The mass of a body is a measure of its inertial property or how much matter it contains. The weight of a body is a measure of the force exerted on it by gravity or the force needed to support it. Gravity on earth gives a body a downward acceleration of about 9.8 m/s². In common parlance, weight is often used as a synonym for mass in weights and measures. For instance, the verb “to weigh” means “to determine the mass of” or “to have a mass of.” The incorrect use of weight in place of mass should be phased out, and the term mass used when mass is meant. The SI unit of mass is the kilogram (kg). In science and technology, the weight of a body in a particular reference frame is defined as the force that gives the body an acceleration equal to the local acceleration of free fall in that reference frame. Thus, the SI unit of the quantity weight defined in this way (force) is the newton (N).

Length

Length is the measurement of the extent of something along its greatest dimension. The SI basic unit of length, or linear measure, is the meter \(\left( \text{m} \right)\). All measurements of length may be made in meters, though the prefixes listed in various tables will often be more convenient. The width of a room may be expressed as about 5 meters \(\left( \text{m} \right)\), whereas a large distance, such as the distance between New York City and Chicago, is better expressed as 1150 kilometers \(\left( \text{km} \right)\). Very small distances can be expressed in units such as the millimeter or the micrometer. The width of a typical human hair is about 10 micrometers \(\left( \mu \text{m} \right)\).

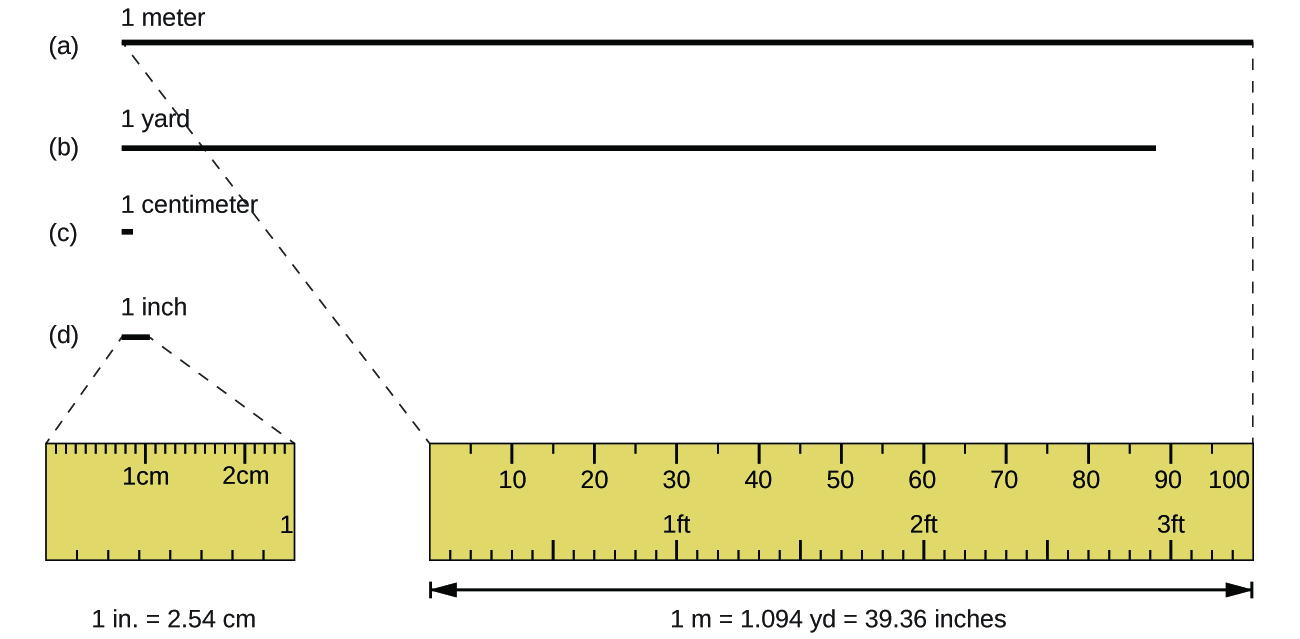
Figure \(\PageIndex{2}\): The relative lengths of 1 m, 1 yd, 1 cm, and 1 in. are shown (not actual size), as well as comparisons of 2.54 cm and 1 in., and of 1 m and 1.094 yd. (CC BY 4.0; OpenStax)

Volume

In addition to the fundamental units, SI also allows for derived units based on a fundamental unit or units. There are many derived units used in science. For example, the derived unit for area comes from the idea that area is defined as width times height. Because both width and height are lengths, they both have the fundamental unit of meter, so the unit of area is meter × meter, or meter² (m²). This is sometimes spoken as "square meters." A unit with a prefix can also be used to derive a unit for area, so we can also have cm², mm², or km² as acceptable units for area.

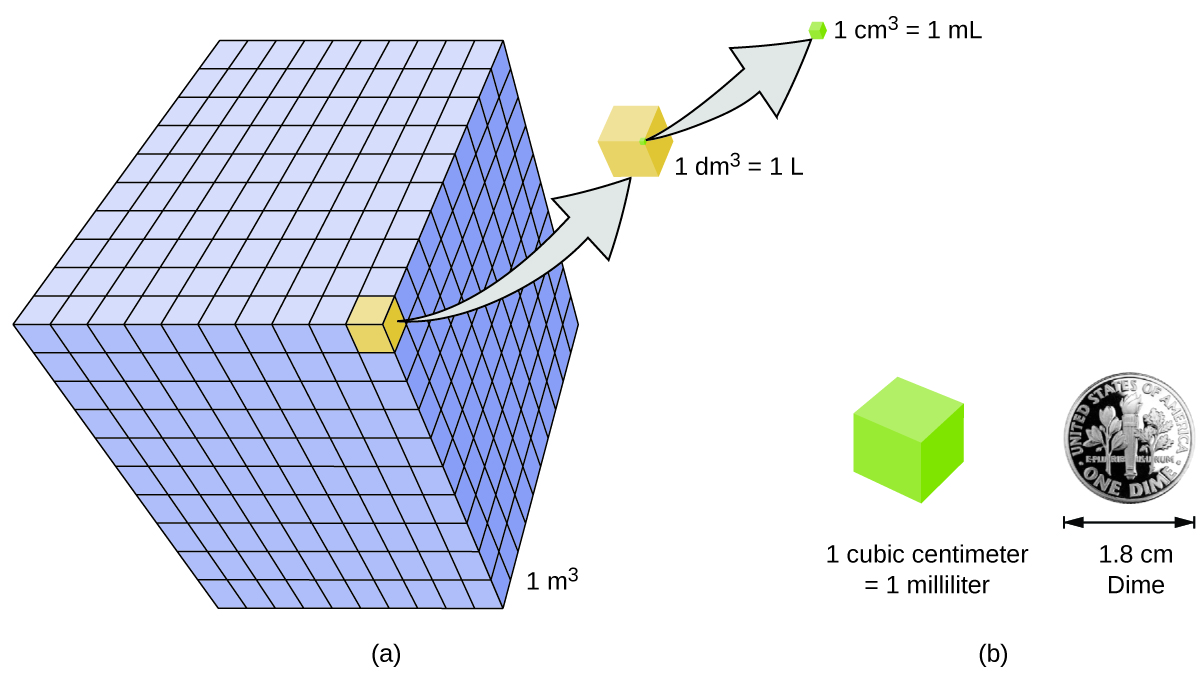
Volume is the amount of space occupied by a sample of matter. The volume of a regular object can be calculated by multiplying its length by its width and its height. Since each of those is a linear measurement, we say that units of volume are derived from units of length. One unit of volume is the cubic meter \(\left( \text{m}^3 \right)\), which is the volume occupied by a cube that measures \(1 \: \text{m}\) on each side. This very large volume is not very convenient for typical use in a chemistry laboratory. A liter \(\left( \text{L} \right)\) is the volume of a cube that measures \(10 \: \text{cm}\) \(\left( 1 \: \text{dm} \right)\) on each side. A liter is thus equal to both \(1000 \: \text{cm}^3\) \(\left( 10 \: \text{cm} \times 10 \: \text{cm} \times 10 \: \text{cm} \right)\) and to \(1 \: \text{dm}^3\). A smaller unit of volume that is commonly used is the milliliter (\(\text{mL}\) - note the capital \(\text{L}\) which is a standard practice). A milliliter is the volume of a cube that measures \(1 \: \text{cm}\) on each side. Therefore, a milliliter is equal to a cubic centimeter \(\left( \text{cm}^3 \right)\). There are \(1000 \: \text{mL}\) in \(1 \: \text{L}\), which is the same as saying that there are \(1000 \: \text{cm}^3\) in \(1 \: \text{dm}^3\).

pproximate Equivalents to Some SI Units

• 1 m ≈ 39.36 in. ≈ 3.28 ft ≈ 1.09 yd
• 1 in. ≈ 2.54 cm
• 1 km ≈ 0.62 mi
• 1 kg ≈ 2.20 lb
• 1 lb ≈ 454 g
• 1 L ≈ 1.06 qt
• 1 qt ≈ 0.946 L

Another definition of a liter is one-tenth of a meter cubed. Because one-tenth of a meter is 10 cm, then a liter is equal to 1,000 cm³ (Figure \(\PageIndex{3}\)). Because 1 L equals 1,000 mL, we conclude that 1 mL equals 1 cm³; thus, these units are interchangeable.

Figure \(\PageIndex{3}\): Units of Volume. (a) The relative volumes are shown for cubes of 1 m³, 1 dm³ (1 L), and 1 cm³ (1 mL) (not to scale). A liter (L) is defined as a cube 1 dm (1/10th of a meter) on a side. A milliliter (mL), 1/1,000th of a liter, is equal to 1 cubic centimeter. (b) The diameter of a dime is compared relative to the edge length of a 1-cm³ (1-mL) cube. (CC BY 4.0; OpenStax)

Units not only are multiplied together but also can be divided. For example, if you are traveling at one meter for every second of time elapsed, your velocity is 1 meter per second, or 1 m/s. The word per implies division, so velocity is determined by dividing a distance quantity by a time quantity. Other units for velocity include kilometers per hour (km/h) or even micrometers per nanosecond (μm/ns). Later, we will see other derived units that can be expressed as fractions.

Temperature

One of the fundamental quantities in science is temperature, which is a measure of the average amount of energy of motion, or kinetic energy, a system contains. Temperatures are expressed using scales that use units called degrees. There are three scales used for reporting temperatures. Figure \(\PageIndex{1}\) compares the three temperature scales.

Figure \(\PageIndex{1}\): Fahrenheit, Celsius, and Kelvin Temperatures. A comparison of the three temperature scales. These thermometers have a red-colored liquid which contains alcohol and food coloring. Silver looking thermometers contain mercury, which is a neurotoxin.

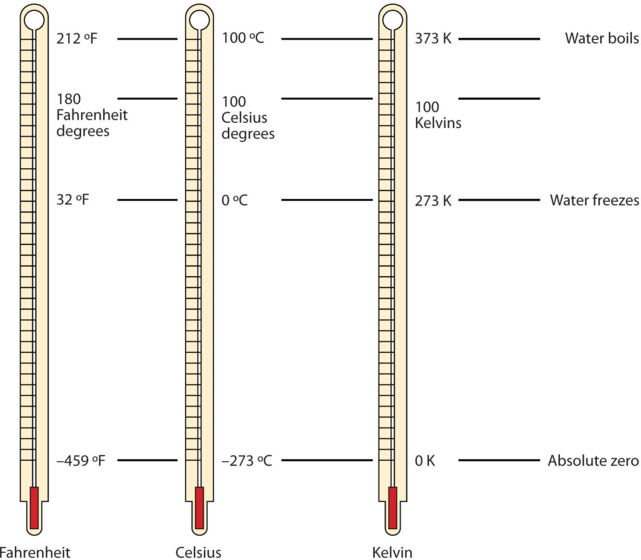
In the United States, the commonly used temperature scale is the Fahrenheit scale (symbolized by °F and spoken as “degrees Fahrenheit”). On this scale, the freezing point of liquid water (the temperature at which liquid water turns to solid ice) is 32 °F, and the boiling point of water (the temperature at which liquid water turns to steam) is 212 °F.

Science also uses other scales to express temperature. For example, the Celsius scale (symbolized by °C and spoken as “degrees Celsius”) defines 0°C as the freezing point of water and 100 °C as the boiling point of water. This scale is divided into 100 divisions between these two landmarks and extended higher and lower as well. By comparing the Fahrenheit and Celsius scales, a conversion between the two scales can be determined:

\[^{\circ}F= \left(^{\circ}C\times \dfrac{9}{5}\right)+32 \label{C2F}\]

Note that science uses the Celsius and Kelvin scales almost exclusively; virtually no practicing chemist expresses laboratory-measured temperatures with the Fahrenheit scale. (In fact, the United States is one of the few countries in the world that still uses the Fahrenheit scale on a daily basis. People driving near the borders of Canada or Mexico may pick up local radio stations on the other side of the border that express the daily weather in degrees Celsius, so do not get confused by their weather reports.)

 The fundamental unit of temperature in SI is the Kelvin (K). The Kelvin temperature scale (note that the name of the scale capitalizes the word Kelvin, but the unit itself is lowercase) uses degrees that are the same size as the Celsius degree, but the numerical scale is shifted up by 273.15 units. That is, the conversion between the Kelvin and Celsius scales is as follows:

\[K=^{\circ}C+273.15 \label{C2K}\]

For most purposes, it is acceptable to use 273 instead of 273.15 in Equation \ref{C2K}.

Note that the Kelvin scale does not use the word degrees; a temperature of 295 K is spoken of as “two hundred ninety-five kelvin” and not “two hundred ninety-five degrees Kelvin.”

The reason that the Kelvin scale is defined this way is that there exists a minimum possible temperature called absolute zero (zero Kelvin). The Kelvin temperature scale is set so that 0 K is absolute zero, and the temperature is counted upward from there.

Contributors and Attributions

• Elizabeth R. Gordon (Furman University)
• Hayden Cox (Furman University, Class of 2018)