Skip to main content
Chemistry LibreTexts

3.7.0.0: Heating Curves and Phase Changes (Problems)

  1. Last updated
  2. Save as PDF
  • Page ID
    210731

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

    ( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\id}{\mathrm{id}}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\kernel}{\mathrm{null}\,}\)

    \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\)

    \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\)

    \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    \( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

    \( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

    \( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vectorC}[1]{\textbf{#1}} \)

    \( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

    \( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

    \( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)

    PROBLEM \(\PageIndex{1}\)

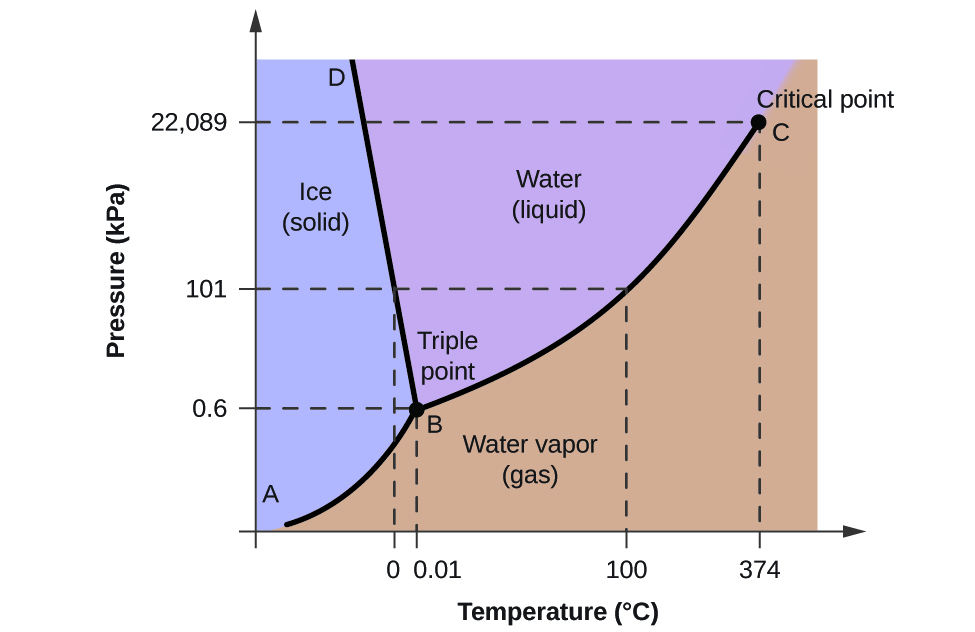
    A graph is shown where the x-axis is labeled “Temperature in degrees Celsius” and the y-axis is labeled “Pressure ( k P a ).” A line extends from the origin of the graph which is labeled “A” sharply upward to a point in the bottom third of the diagram labeled “B” where it branches into a line that slants slightly backward until it hits the highest point on the y-axis labeled “D” and a second line that extends to the upper right corner of the graph labeled “C”. C is labeled “Critical point, with a dotted line extending downward to the x-axis labeled 374 degrees Celsius, and another dotted line extending to the y-axis labeled 22,089 k P a. The two lines bisect the graph area to create three sections, labeled “Ice (solid)” near the middle left, “Water (liquid)” in the top middle and “Water vapor (gas)” near the bottom middle. Point B is labeled “Triple point” and has a dotted line extending downward to the x-axis labeled 0.01, and another dotted line extending to the y-axis labeled 0.6. Halfway between points B and C a dotted line extends from the originally discussed line downward to the point 100 degrees Celsius on the x-axis, and another dotted line extends to the y-axis at 101 k P a. Another dotted line extends from this dotted line downward at 0 degrees Celsius.

    From the phase diagram for water, determine the state of water at:

    1. 35 °C and 85 kPa
    2. −15 °C and 40 kPa
    3. −15 °C and 0.1 kPa
    4. 75 °C and 3 kPa
    5. 40 °C and 0.1 kPa
    6. 60 °C and 50 kPa
    Answer a

    Liquid

    Answer b

    solid

    Answer c

    solid

    Answer d

    gas

    Answer e

    gas

    Answer f

    liquid

    PROBLEM \(\PageIndex{2}\)

    Evaporation of sweat requires energy and thus take excess heat away from the body. Some of the water that you drink may eventually be converted into sweat and evaporate. If you drink a 20-ounce bottle of water that had been in the refrigerator at 3.8 °C, how much heat is needed to convert all of that water into sweat and then to vapor?? (Note: Your body temperature is 36.6 °C. For the purpose of solving this problem, assume that the thermal properties of sweat are the same as for water.)

    Answer

    81.17 kJ

    PROBLEM \(\PageIndex{3}\)

    How much heat is required to convert 422 g of liquid H2O at 23.5 °C into steam at 150 °C?

    Answer

    1130 kJ

    PROBLEM \(\PageIndex{4}\)

    Titanium tetrachloride, TiCl4, has a melting point of −23.2 °C and has a ΔH fusion = 9.37 kJ/mol.

    1. How much energy is required to melt 263.1 g TiCl4?
    2. For TiCl4, which will likely have the larger magnitude: ΔH fusion or ΔH vaporization? Explain your reasoning.
    Answer a

    13.0 kJ

    Answer b

    It is likely that the heat of vaporization will have a larger magnitude since in the case of vaporization the intermolecular interactions have to be completely overcome, while melting weakens or destroys only some of them.

    PROBLEM \(\PageIndex{5}\)

    A graph is shown where the x-axis is labeled “Temperature in degrees Celsius” and the y-axis is labeled “Pressure ( k P a ).” A line extends from the origin of the graph which is labeled “A” sharply upward to a point in the bottom third of the diagram labeled “B” where it branches into a line that slants slightly backward until it hits the highest point on the y-axis labeled “D” and a second line that extends to the upper right corner of the graph labeled “C”. C is labeled “Critical point, with a dotted line extending downward to the x-axis labeled 374 degrees Celsius, and another dotted line extending to the y-axis labeled 22,089 k P a. The two lines bisect the graph area to create three sections, labeled “Ice (solid)” near the middle left, “Water (liquid)” in the top middle and “Water vapor (gas)” near the bottom middle. Point B is labeled “Triple point” and has a dotted line extending downward to the x-axis labeled 0.01, and another dotted line extending to the y-axis labeled 0.6. Halfway between points B and C a dotted line extends from the originally discussed line downward to the point 100 degrees Celsius on the x-axis, and another dotted line extends to the y-axis at 101 k P a. Another dotted line extends from this dotted line downward at 0 degrees Celsius.

    What phase changes will take place when water is subjected to varying pressure at a constant temperature of 0.005 °C? At 40 °C? At −40 °C?

    Answer

    0.005 °C: gas to solid to liquid

    40 °C: gas to liquid

    −40 °C: gas to solid to liquid (maybe)

    PROBLEM \(\PageIndex{6}\)

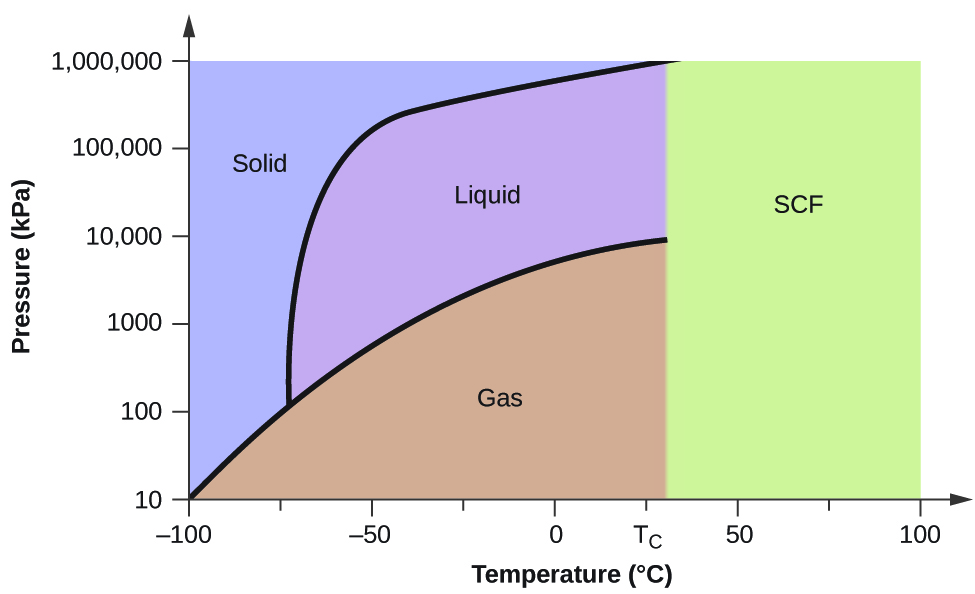
    CNX_Chem_10_04_CO2phasdi.jpg

    From the phase diagram for carbon dioxide, determine the state of CO2 at:

    1. 20 °C and 1000 kPa
    2. 10 °C and 2000 kPa
    3. 10 °C and 100 kPa
    4. −40 °C and 500 kPa
    5. −80 °C and 1500 kPa
    6. −80 °C and 10 kPa
    Answer a

    liquid

    Answer b

    solid

    Answer c

    gas

    Answer d

    gas

    Answer e

    gas

    Answer f

    gas

    PROBLEM \(\PageIndex{7}\)

    CNX_Chem_10_04_CO2phasdi.jpg

    Determine the phase changes that carbon dioxide undergoes as the pressure changes if the temperature is held at −50 °C? If the temperature is held at −40 °C? At 20 °C?

    Answer

    −50 °C: gas to liquid to solid

    −40 °C: gas to liquid to solid

    20 °C: gas to liquid to solid

    PROBLEM \(\PageIndex{8}\)

    CNX_Chem_10_04_CO2phasdi.jpg

    Dry ice, CO2(s), does not melt at atmospheric pressure. It sublimes at a temperature of −78 °C. What is the lowest pressure at which CO2(s) will melt to give CO2(l)? At approximately what temperature will this occur?

    Answer

    Dry ice, CO2(s), will melt to give CO2(l) at 5.11 atm at −56.6 °C, the triple point of carbon dioxide.

    PROBLEM \(\PageIndex{9}\)

    Elemental carbon has one gas phase, one liquid phase, and three different solid phases, as shown in the phase diagram:

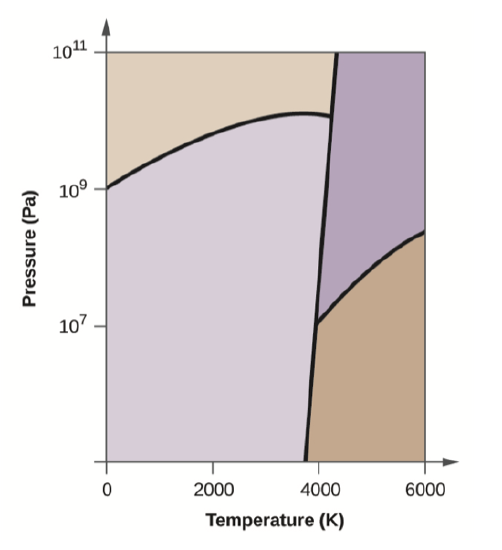
    Screen Shot 2019-01-02 at 1.13.44 PM.png

    1. On the phase diagram, label the gas and liquid regions.
    2. Graphite is the most stable phase of carbon at normal conditions. On the phase diagram, label the graphite phase.
    3. If graphite at normal conditions is heated to 2500 K while the pressure is increased to 1010 Pa, it is converted into diamond. Label the diamond phase.
    4. Circle each triple point on the phase diagram.
    5. In what phase does carbon exist at 5000 K and 108 Pa?
    6. If the temperature of a sample of carbon increases from 3000 K to 5000 K at a constant pressure of 106 Pa, which phase transition occurs, if any?
    Answer a

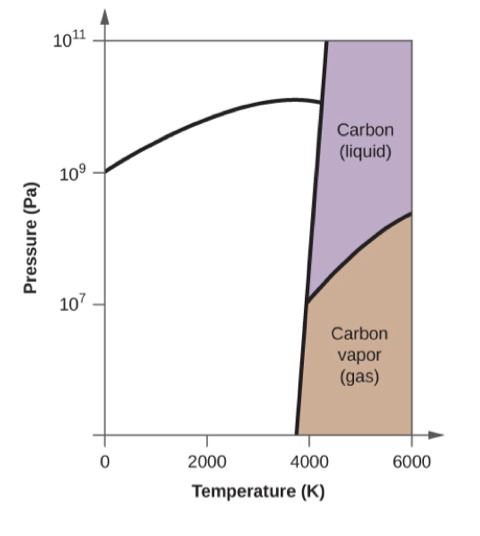
    Screen Shot 2019-01-02 at 1.16.17 PM.png

    Answer b

    Screen Shot 2019-01-02 at 1.16.25 PM.png

    Answer c

    Screen Shot 2019-01-02 at 1.16.32 PM.png

    Answer d

    Screen Shot 2019-01-02 at 1.16.37 PM.png

    Answer e

    liquid

    Answer f

    sublimation

    Have a video solution request?

    Let your professors know here.

    ***Please know that you are helping future students - videos will be made in time for next term's class.

    Contributors and Attributions

    Feedback

    Think one of the answers above is wrong? Let us know here.

    3.7.0.0: Heating Curves and Phase Changes (Problems) is shared under a not declared license and was authored, remixed, and/or curated by LibreTexts.

    1. Back to top
    • Was this article helpful?

    Recommended articles

    1. Article type
      Section or Page
      Show Page TOC
      no on page
    2. Tags
      1. source[1]-chem-119749