2.1.4: Calculating Atomic Masses
- Page ID
- 210625
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
Learning Objectives
- Define the atomic mass unit and average atomic mass
- Calculate average atomic mass and isotopic abundance
- Define the amount unit mole and the related quantity Avogadro’s number
- Explain the relation between mass, moles, and numbers of atoms or molecules, and perform calculations deriving these quantities from one another
Video \(\PageIndex{1}\): A review of counting subatomic particles and a preview of isotopes and relative atomic mass.
Isotopes
The symbol for a specific isotope of any element is written by placing the mass number as a superscript to the left of the element symbol (Figure \(\PageIndex{4}\)). The atomic number is sometimes written as a subscript preceding the symbol, but since this number defines the element’s identity, as does its symbol, it is often omitted. For example, magnesium exists as a mixture of three isotopes, each with an atomic number of 12 and with mass numbers of 24, 25, and 26, respectively. These isotopes can be identified as 24Mg, 25Mg, and 26Mg. These isotope symbols are read as “element, mass number” and can be symbolized consistent with this reading. For instance, 24Mg is read as “magnesium 24,” and can be written as “magnesium-24” or “Mg-24.” 25Mg is read as “magnesium 25,” and can be written as “magnesium-25” or “Mg-25.” All magnesium atoms have 12 protons in their nucleus. They differ only because a 24Mg atom has 12 neutrons in its nucleus, a 25Mg atom has 13 neutrons, and a 26Mg has 14 neutrons.
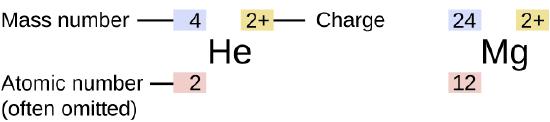
Figure \(\PageIndex{1}\): The symbol for an atom indicates the element via its usual two-letter symbol, the mass number as a left superscript, the atomic number as a left subscript (sometimes omitted), and the charge as a right superscript.
Information about the naturally occurring isotopes of elements with atomic numbers 1 through 10 is given in Table \(\PageIndex{2}\). Note that in addition to standard names and symbols, the isotopes of hydrogen are often referred to using common names and accompanying symbols. Hydrogen-2, symbolized 2H, is also called deuterium and sometimes symbolized D. Hydrogen-3, symbolized 3H, is also called tritium and sometimes symbolized T.
| Element | Symbol | Atomic Number | Number of Protons | Number of Neutrons | Mass (amu) | % Natural Abundance |
|---|---|---|---|---|---|---|
| hydrogen | \(\ce{^1_1H}\) (protium) |
1 | 1 | 0 | 1.0078 | 99.989 |
| \(\ce{^2_1H}\) (deuterium) |
1 | 1 | 1 | 2.0141 | 0.0115 | |
| \(\ce{^3_1H}\) (tritium) |
1 | 1 | 2 | 3.01605 | — (trace) | |
| helium | \(\ce{^3_2He}\) | 2 | 2 | 1 | 3.01603 | 0.00013 |
| \(\ce{^4_2He}\) | 2 | 2 | 2 | 4.0026 | 100 | |
| lithium | \(\ce{^6_3Li}\) | 3 | 3 | 3 | 6.0151 | 7.59 |
| \(\ce{^7_3Li}\) | 3 | 3 | 4 | 7.0160 | 92.41 | |
| beryllium | \(\ce{^9_4Be}\) | 4 | 4 | 5 | 9.0122 | 100 |
| boron | \(\ce{^{10}_5B}\) | 5 | 5 | 5 | 10.0129 | 19.9 |
| \(\ce{^{11}_5B}\) | 5 | 5 | 6 | 11.0093 | 80.1 | |
| carbon | \(\ce{^{12}_6C}\) | 6 | 6 | 6 | 12.0000 | 98.89 |
| \(\ce{^{13}_6C}\) | 6 | 6 | 7 | 13.0034 | 1.11 | |
| \(\ce{^{14}_6C}\) | 6 | 6 | 8 | 14.0032 | — (trace) | |
| nitrogen | \(\ce{^{14}_7N}\) | 7 | 7 | 7 | 14.0031 | 99.63 |
| \(\ce{^{15}_7N}\) | 7 | 7 | 8 | 15.0001 | 0.37 | |
| oxygen | \(\ce{^{16}_8O}\) | 8 | 8 | 8 | 15.9949 | 99.757 |
| \(\ce{^{17}_8O}\) | 8 | 8 | 9 | 16.9991 | 0.038 | |
| \(\ce{^{18}_8O}\) | 8 | 8 | 10 | 17.9992 | 0.205 | |
| fluorine | \(\ce{^{19}_9F}\) | 9 | 9 | 10 | 18.9984 | 100 |
| neon | \(\ce{^{20}_{10}Ne}\) | 10 | 10 | 10 | 19.9924 | 90.48 |
| \(\ce{^{21}_{10}Ne}\) | 10 | 10 | 11 | 20.9938 | 0.27 | |
| \(\ce{^{22}_{10}Ne}\) | 10 | 10 | 12 | 21.9914 | 9.25 |
Use this Build an Atom simulator to build atoms of the first 10 elements, see which isotopes exist, check nuclear stability, and gain experience with isotope symbols.
Atomic Mass
Because each proton and each neutron contribute approximately one amu to the mass of an atom, and each electron contributes far less, the atomic mass of a single atom is approximately equal to its mass number (a whole number). However, the average masses of atoms of most elements are not whole numbers because most elements exist naturally as mixtures of two or more isotopes.
The mass of an element shown in a periodic table or listed in a table of atomic masses is a weighted, average mass of all the isotopes present in a naturally occurring sample of that element. This is equal to the sum of each individual isotope’s mass multiplied by its fractional abundance.
\[\mathrm{average\: mass}=\sum_{i}(\mathrm{fractional\: abundance\times isotopic\: mass})_i\]
For example, the element boron is composed of two isotopes: About 19.9% of all boron atoms are 10B with a mass of 10.0129 amu, and the remaining 80.1% are 11B with a mass of 11.0093 amu. The average atomic mass for boron is calculated to be:
\[\begin{align*}
\textrm{boron average mass} &=\mathrm{(0.199\times10.0129\: amu)+(0.801\times11.0093\: amu)}\\
&=\mathrm{1.99\: amu+8.82\: amu}\\
&=\mathrm{10.81\: amu}
\end{align*}\]
It is important to understand that no single boron atom weighs exactly 10.8 amu; 10.8 amu is the average mass of all boron atoms, and individual boron atoms weigh either approximately 10 amu or 11 amu.
Example \(\PageIndex{1}\): Calculation of Average Atomic Mass
A meteorite found in central Indiana contains traces of the noble gas neon picked up from the solar wind during the meteorite’s trip through the solar system. Analysis of a sample of the gas showed that it consisted of 91.84% 20Ne (mass 19.9924 amu), 0.47% 21Ne (mass 20.9940 amu), and 7.69% 22Ne (mass 21.9914 amu). What is the average mass of the neon in the solar wind?
Solution
\[\begin{align*}
\mathrm{average\: mass} &=\mathrm{(0.9184\times19.9924\: amu)+(0.0047\times20.9940\: amu)+(0.0769\times21.9914\: amu)}\\
&=\mathrm{(18.36+0.099+1.69)\:amu}\\
&=\mathrm{20.15\: amu}
\end{align*}\]
The average mass of a neon atom in the solar wind is 20.15 amu. (The average mass of a terrestrial neon atom is 20.1796 amu. This result demonstrates that we may find slight differences in the natural abundance of isotopes, depending on their origin.)
Exercise \(\PageIndex{1}\)
A sample of magnesium is found to contain 78.70% of 24Mg atoms (mass 23.98 amu), 10.13% of 25Mg atoms (mass 24.99 amu), and 11.17% of 26Mg atoms (mass 25.98 amu). Calculate the average mass of a Mg atom.
- Answer
-
24.31 amu
We can also do variations of this type of calculation, as shown in the next example.
Example \(\PageIndex{2}\): Calculation of Percent Abundance
Naturally occurring chlorine consists of 35Cl (mass 34.96885 amu) and 37Cl (mass 36.96590 amu), with an average mass of 35.453 amu. What is the percent composition of Cl in terms of these two isotopes?
Solution
The average mass of chlorine is the fraction that is 35Cl times the mass of 35Cl plus the fraction that is 37Cl times the mass of 37Cl.
\[\mathrm{average\: mass=(fraction\: of\: ^{35}Cl\times mass\: of\: ^{35}Cl)+(fraction\: of\: ^{37}Cl\times mass\: of\: ^{37}Cl)}\]
If we let x represent the fraction that is 35Cl, then the fraction that is 37Cl is represented by 1.00 − x.
(The fraction that is 35Cl + the fraction that is 37Cl must add up to 1, so the fraction of 37Cl must equal 1.00 − the fraction of 35Cl.)
Substituting this into the average mass equation, we have:
\[\begin{align*}
\mathrm{35.453\: amu} &=(x\times 34.96885\: \ce{amu})+[(1.00-x)\times 36.96590\: \ce{amu}]\\
35.453 &=34.96885x+36.96590-36.96590x\\
1.99705x &=1.513\\
x&=\dfrac{1.513}{1.99705}=0.7576
\end{align*}\]
So solving yields: x = 0.7576, which means that 1.00 − 0.7576 = 0.2424. Therefore, chlorine consists of 75.76% 35Cl and 24.24% 37Cl.
Exercise \(\PageIndex{2}\)
Naturally occurring copper consists of 63Cu (mass 62.9296 amu) and 65Cu (mass 64.9278 amu), with an average mass of 63.546 amu. What is the percent composition of Cu in terms of these two isotopes?
- Answer
-
69.15% Cu-63 and 30.85% Cu-65
Use this simulator to make mixtures of the main isotopes of the first 18 elements, gain experience with average atomic mass, and check naturally occurring isotope ratios.
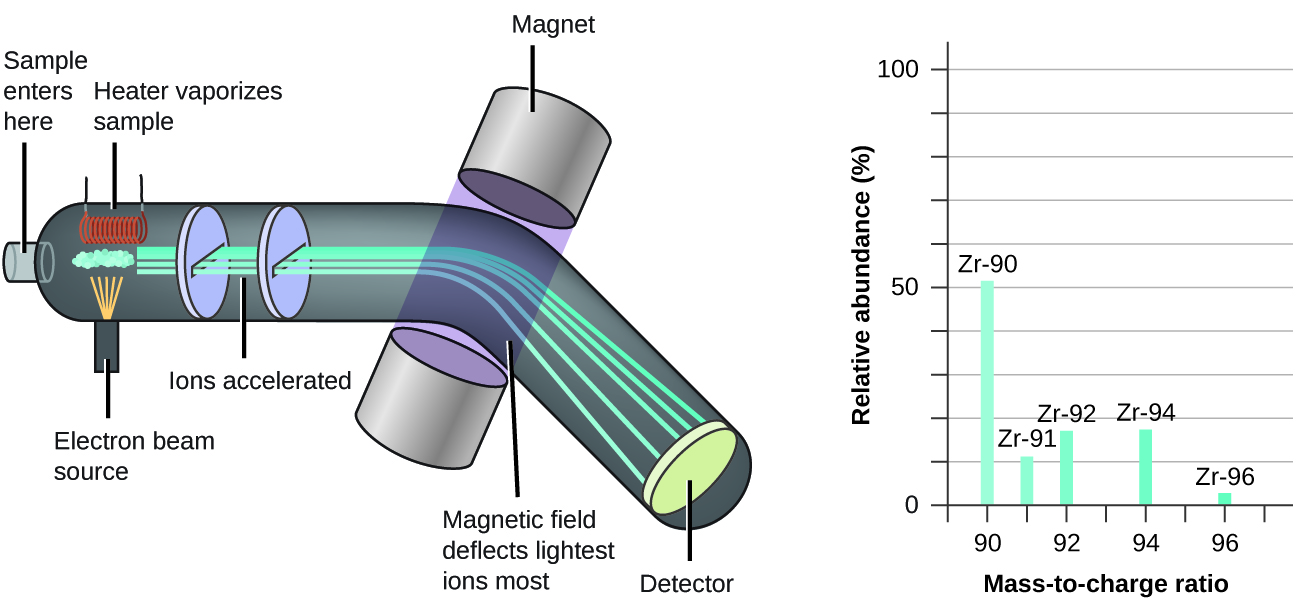
Figure \(\PageIndex{2}\): Analysis of zirconium in a mass spectrometer produces a mass spectrum with peaks showing the different isotopes of Zr.
The occurrence and natural abundances of isotopes can be experimentally determined using an instrument called a mass spectrometer. Mass spectrometry (MS) is widely used in chemistry, forensics, medicine, environmental science, and many other fields to analyze and help identify the substances in a sample of material. In a typical mass spectrometer (Figure \(\PageIndex{5}\)), the sample is vaporized and exposed to a high-energy electron beam that causes the sample’s atoms (or molecules) to become electrically charged, typically by losing one or more electrons. These cations then pass through a (variable) electric or magnetic field that deflects each cation’s path to an extent that depends on both its mass and charge (similar to how the path of a large steel ball bearing rolling past a magnet is deflected to a lesser extent that that of a small steel BB). The ions are detected, and a plot of the relative number of ions generated versus their mass-to-charge ratios (a mass spectrum) is made. The height of each vertical feature or peak in a mass spectrum is proportional to the fraction of cations with the specified mass-to-charge ratio. Since its initial use during the development of modern atomic theory, MS has evolved to become a powerful tool for chemical analysis in a wide range of applications.
Video \(\PageIndex{2}\): Watch this video from the Royal Society for Chemistry for a brief description of the rudiments of mass spectrometry.
The Mole
The identity of a substance is defined not only by the types of atoms or ions it contains, but by the quantity of each type of atom or ion. For example, water, H2O, and hydrogen peroxide, H2O2, are alike in that their respective molecules are composed of hydrogen and oxygen atoms. However, because a hydrogen peroxide molecule contains two oxygen atoms, as opposed to the water molecule, which has only one, the two substances exhibit very different properties. Today, we possess sophisticated instruments that allow the direct measurement of these defining microscopic traits; however, the same traits were originally derived from the measurement of macroscopic properties (the masses and volumes of bulk quantities of matter) using relatively simple tools (balances and volumetric glassware). This experimental approach required the introduction of a new unit for amount of substances, the mole, which remains indispensable in modern chemical science.
The mole is an amount unit similar to familiar units like pair, dozen, gross, etc. It provides a specific measure of the number of atoms or molecules in a bulk sample of matter. A mole is defined as the amount of substance containing the same number of discrete entities (such as atoms, molecules, and ions) as the number of atoms in a sample of pure 12C weighing exactly 12 g. One Latin connotation for the word “mole” is “large mass” or “bulk,” which is consistent with its use as the name for this unit. The mole provides a link between an easily measured macroscopic property, bulk mass, and an extremely important fundamental property, number of atoms, molecules, and so forth.
The number of entities composing a mole has been experimentally determined to be \(6.02214179 \times 10^{23}\), a fundamental constant named Avogadro’s number (NA) or the Avogadro constant in honor of Italian scientist Amedeo Avogadro. This constant is properly reported with an explicit unit of “per mole,” a conveniently rounded version being \(6.022 \times 10^{23}/\ce{mol}\).
Video \(\PageIndex{3}\): What is Avogadro's Number?
Consistent with its definition as an amount unit, 1 mole of any element contains the same number of atoms as 1 mole of any other element. The masses of 1 mole of different elements, however, are different, since the masses of the individual atoms are drastically different. The molar mass of an element (or compound) is the mass in grams of 1 mole of that substance, a property expressed in units of grams per mole (g/mol) (Figure \(\PageIndex{3}\)).

Figure \(\PageIndex{3}\): Each sample contains \(6.022 \times 10^{23}\) atoms —1.00 mol of atoms. From left to right (top row): 65.4 g zinc, 12.0 g carbon, 24.3 g magnesium, and 63.5 g copper. From left to right (bottom row): 32.1 g sulfur, 28.1 g silicon, 207 g lead, and 118.7 g tin. (credit: modification of work by Mark Ott).
Because the definitions of both the mole and the atomic mass unit are based on the same reference substance, 12C, the molar mass of any substance is numerically equivalent to its atomic or formula weight in amu. Per the amu definition, a single 12C atom weighs 12 amu (its atomic mass is 12 amu). The former definition of the mole was that a mole was 12 g of 12C contains 1 mole of 12C atoms (its molar mass is 12 g/mol). This relationship holds for all elements, since their atomic masses are measured relative to that of the amu-reference substance, 12C. Extending this principle, the molar mass of a compound in grams is likewise numerically equivalent to its formula mass in amu (Figure \(\PageIndex{4}\)). On May 20, 2019 the definition was permanently changed to Avogadro's number: a mole is \(6.02214179 \times 10^{23}\) of any object, from atoms to apples.1

Figure \(\PageIndex{4}\): Each sample contains \(6.022 \times 10^{23}\) molecules or formula units—1.00 mol of the compound or element. Clock-wise from the upper left: 130.2 g of C8H17OH (1-octanol, formula mass 130.2 amu), 454.4 g of HgI2 (mercury(II) iodide, formula mass 454.4 amu), 32.0 g of CH3OH (methanol, formula mass 32.0 amu) and 256.5 g of S8 (sulfur, formula mass 256.5 amu). (credit: Sahar Atwa).
| Element | Average Atomic Mass (amu) | Molar Mass (g/mol) | Atoms/Mole |
|---|---|---|---|
| C | 12.01 | 12.01 | \(6.022 \times 10^{23}\) |
| H | 1.008 | 1.008 | \(6.022 \times 10^{23}\) |
| O | 16.00 | 16.00 | \(6.022 \times 10^{23}\) |
| Na | 22.99 | 22.99 | \(6.022 \times 10^{23}\) |
| Cl | 33.45 | 35.45 | \(6.022 \times 10^{23}\) |
While atomic mass and molar mass are numerically equivalent, keep in mind that they are vastly different in terms of scale, as represented by the vast difference in the magnitudes of their respective units (amu versus g). To appreciate the enormity of the mole, consider a small drop of water after a rainfall. Although this represents just a tiny fraction of 1 mole of water (~18 g), it contains more water molecules than can be clearly imagined. If the molecules were distributed equally among the roughly seven billion people on earth, each person would receive more than 100 billion molecules.
Video \(\PageIndex{4}\): The mole is used in chemistry to represent \(6.022 \times 10^{23}\) of something, but it can be difficult to conceptualize such a large number. Watch this video and then complete the “Think” questions that follow. Explore more about the mole by reviewing the information under “Dig Deeper.”
The relationships between formula mass, the mole, and Avogadro’s number can be applied to compute various quantities that describe the composition of substances and compounds. For example, if we know the mass and chemical composition of a substance, we can determine the number of moles and calculate number of atoms or molecules in the sample. Likewise, if we know the number of moles of a substance, we can derive the number of atoms or molecules and calculate the substance’s mass.
Example \(\PageIndex{3}\): Deriving Moles from Grams for an Element
According to nutritional guidelines from the US Department of Agriculture, the estimated average requirement for dietary potassium is 4.7 g. What is the estimated average requirement of potassium in moles?
Solution
The mass of K is provided, and the corresponding amount of K in moles is requested. Referring to the periodic table, the atomic mass of K is 39.10 amu, and so its molar mass is 39.10 g/mol. The given mass of K (4.7 g) is a bit more than one-tenth the molar mass (39.10 g), so a reasonable “ballpark” estimate of the number of moles would be slightly greater than 0.1 mol.
The molar amount of a substance may be calculated by dividing its mass (g) by its molar mass (g/mol):

The factor-label method supports this mathematical approach since the unit “g” cancels and the answer has units of “mol:”
\[ \mathrm{4.7\; \cancel{g} K \left ( \dfrac{mol\; K}{39.10\;\cancel{g}}\right)=0.12\;mol\; K} \nonumber\]
The calculated magnitude (0.12 mol K) is consistent with our ballpark expectation, since it is a bit greater than 0.1 mol.
Exercise \(\PageIndex{3}\): Beryllium
Beryllium is a light metal used to fabricate transparent X-ray windows for medical imaging instruments. How many moles of Be are in a thin-foil window weighing 3.24 g?
- Answer
-
0.360 mol
Example \(\PageIndex{4}\): Deriving Grams from Moles for an Element
A liter of air contains \(9.2 \times 10^{−4}\) mol argon. What is the mass of Ar in a liter of air?
Solution
The molar amount of Ar is provided and must be used to derive the corresponding mass in grams. Since the amount of Ar is less than 1 mole, the mass will be less than the mass of 1 mole of Ar, approximately 40 g. The molar amount in question is approximately one-one thousandth (~10−3) of a mole, and so the corresponding mass should be roughly one-one thousandth of the molar mass (~0.04 g):

In this case, logic dictates (and the factor-label method supports) multiplying the provided amount (mol) by the molar mass (g/mol):
\[\mathrm{9.2 \times10^{-4}\; \cancel{mol} \; Ar \left( \dfrac{39.95\;g}{\cancel{mol}\;Ar} \right)=0.037\;g\; Ar} \nonumber\]
The result is in agreement with our expectations, around 0.04 g Ar.
Exercise \(\PageIndex{4}\)
What is the mass of 2.561 mol of gold?
- Answer
-
504.4 g
Example \(\PageIndex{6}\): Deriving Number of Atoms from Mass for an Element
Copper is commonly used to fabricate electrical wire (Figure \(\PageIndex{6}\)). How many copper atoms are in 5.00 g of copper wire?

Figure \(\PageIndex{6}\): Copper wire is composed of many, many atoms of Cu. (credit: Emilian Robert Vicol)
Solution
The number of Cu atoms in the wire may be conveniently derived from its mass by a two-step computation: first calculating the molar amount of Cu, and then using Avogadro’s number (NA) to convert this molar amount to number of Cu atoms:

Considering that the provided sample mass (5.00 g) is a little less than one-tenth the mass of 1 mole of Cu (~64 g), a reasonable estimate for the number of atoms in the sample would be on the order of one-tenth NA, or approximately 1022 Cu atoms. Carrying out the two-step computation yields:
\[\mathrm{5.00\:\cancel{g}\:Cu\left(\dfrac{\cancel{mol}\:Cu}{63.55\:\cancel{g}}\right)\left(\dfrac{6.022\times10^{23}\:atoms}{\cancel{mol}}\right)=4.74\times10^{22}\:atoms\: of\: copper}\]
The factor-label method yields the desired cancellation of units, and the computed result is on the order of 1022 as expected.
Exercise \(\PageIndex{6}\)
A prospector panning for gold in a river collects 15.00 g of pure gold. How many Au atoms are in this quantity of gold?
- Answer
-
\(4.586 \times 10^{22}\; Au\) atoms
Example \(\PageIndex{7}\): Deriving Moles from Grams for a Compound
Our bodies synthesize protein from amino acids. One of these amino acids is glycine, which has the molecular formula C2H5O2N. How many moles of glycine molecules are contained in 28.35 g of glycine?
Solution
We can derive the number of moles of a compound from its mass following the same procedure we used for an element in Example \(\PageIndex{6}\):

The molar mass of glycine is required for this calculation, and it is computed in the same fashion as its molecular mass. One mole of glycine, C2H5O2N, contains 2 moles of carbon, 5 moles of hydrogen, 2 moles of oxygen, and 1 mole of nitrogen:
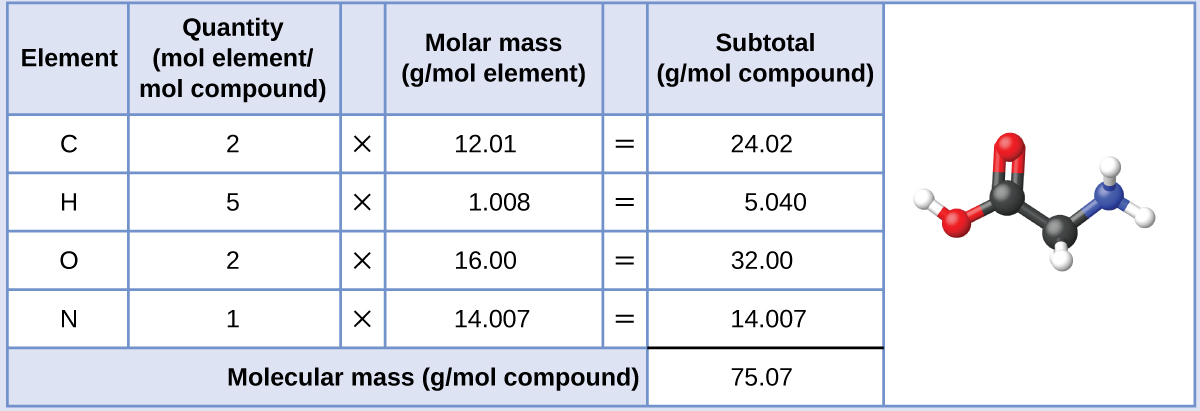
The provided mass of glycine (~28 g) is a bit more than one-third the molar mass (~75 g/mol), so we would expect the computed result to be a bit greater than one-third of a mole (~0.33 mol). Dividing the compound’s mass by its molar mass yields:
\[\mathrm{28.35\:\cancel{g}\:glycine\left(\dfrac{mol\: glycine}{75.07\:\cancel{g}}\right)=0.378\:mol\: glycine} \nonumber\]
This result is consistent with our rough estimate.
Exercise \(\PageIndex{7}\)
How many moles of sucrose, \(C_{12}H_{22}O_{11}\), are in a 25-g sample of sucrose?
- Answer
-
0.073 mol
Example \(\PageIndex{8}\): Deriving Grams from Moles for a Compound
Vitamin C is a covalent compound with the molecular formula C6H8O6. The recommended daily dietary allowance of vitamin C for children aged 4–8 years is 1.42 × 10−4 mol. What is the mass of this allowance in grams?
Solution
As for elements, the mass of a compound can be derived from its molar amount as shown:

The molar mass for this compound is computed to be 176.124 g/mol. The given number of moles is a very small fraction of a mole (~10−4 or one-ten thousandth); therefore, we would expect the corresponding mass to be about one-ten thousandth of the molar mass (~0.02 g). Performing the calculation, we get:
This is consistent with the anticipated result.
Exercise \(\PageIndex{8}\)
What is the mass of 0.443 mol of hydrazine, \(N_2H_4\)?
- Answer
-
14.2 g
Example \(\PageIndex{9}\): Deriving the Number of Molecules from the Compound Mass
A packet of an artificial sweetener contains 40.0 mg of saccharin (C7H5NO3S), which has the structural formula:
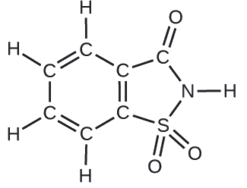
Given that saccharin has a molar mass of 183.18 g/mol, how many saccharin molecules are in a 40.0-mg (0.0400-g) sample of saccharin? How many carbon atoms are in the same sample?
Solution
The number of molecules in a given mass of compound is computed by first deriving the number of moles, as demonstrated in Example \(\PageIndex{8}\), and then multiplying by Avogadro’s number:

Using the provided mass and molar mass for saccharin yields:
\[\mathrm{0.0400\:\cancel{g}\:\ce{C7H5NO3S}\left(\dfrac{\cancel{mol}\:\ce{C7H5NO3S}}{183.18\:\cancel{g}\:\ce{C7H5NO3S}}\right)\left(\dfrac{6.022\times10^{23}\:\ce{C7H5NO3S}\:molecules}{1\:\cancel{mol}\:\ce{C7H5NO3S}}\right)}\\
=\mathrm{1.31\times10^{20}\:\ce{C7H5NO3S}\:molecules}\]
The compound’s formula shows that each molecule contains seven carbon atoms, and so the number of C atoms in the provided sample is:
\[\mathrm{1.31\times10^{20}\:\ce{C7H5NO3S}\: molecules\left(\dfrac{7\:C\: atoms}{1\:\ce{C7H5NO3S}\: molecule}\right)=9.20\times10^{21}\:C\: atoms} \nonumber\]
Exercise \(\PageIndex{9}\)
How many \(C_4H_{10}\) molecules are contained in 9.213 g of this compound? How many hydrogen atoms?
- Answer
-
- \(9.545 \times 10^{22}\; \text{molecules}\; C_4H_{10}\)
- \(9.545 \times 10^{23 }\;\text{atoms}\; H\)
Video \(\PageIndex{5}\): A preview of some of the uses we will have for moles in upcoming units
Summary
Video \(\PageIndex{6}\): Watch this video for a review of relative atomic mass and isotopes.
An atom consists of a small, positively charged nucleus surrounded by electrons. The nucleus contains protons and neutrons; its diameter is about 100,000 times smaller than that of the atom. The mass of one atom is usually expressed in atomic mass units (amu), which is referred to as the atomic mass. An amu is defined as exactly \(1/12\) of the mass of a carbon-12 atom and is equal to 1.6605 \(\times\) 10−24 g.
Protons are relatively heavy particles with a charge of 1+ and a mass of 1.0073 amu. Neutrons are relatively heavy particles with no charge and a mass of 1.0087 amu. Electrons are light particles with a charge of 1− and a mass of 0.00055 amu. The number of protons in the nucleus is called the atomic number (Z) and is the property that defines an atom’s elemental identity. The sum of the numbers of protons and neutrons in the nucleus is called the mass number and, expressed in amu, is approximately equal to the mass of the atom. An atom is neutral when it contains equal numbers of electrons and protons.
Isotopes of an element are atoms with the same atomic number but different mass numbers; isotopes of an element, therefore, differ from each other only in the number of neutrons within the nucleus. When a naturally occurring element is composed of several isotopes, the atomic mass of the element represents the average of the masses of the isotopes involved. A chemical symbol identifies the atoms in a substance using symbols, which are one-, two-, or three-letter abbreviations for the atoms.
Looking Beyond
Video \(\PageIndex{7}\): Remember our exploration into the size of an atom last week? This video goes deeper into investigating the size of the subatomic particles we just discussed.
Footnotes
1. Read more about the redefinition of SI units including the kilogram here (Laura Howe, CE&N, Nov. 16, 2018).
Key Equations
- \(\mathrm{average\: mass}=\sum_{i}(\mathrm{fractional\: abundance \times isotopic\: mass})_i\)
Glossary
- anion
- negatively charged atom or molecule (contains more electrons than protons)
- atomic mass
- average mass of atoms of an element, expressed in amu
- atomic mass unit (amu)
- (also, unified atomic mass unit, u, or Dalton, Da) unit of mass equal to \(\dfrac{1}{12}\) of the mass of a 12C atom
- atomic number (Z)
- number of protons in the nucleus of an atom
- cation
- positively charged atom or molecule (contains fewer electrons than protons)
- chemical symbol
- one-, two-, or three-letter abbreviation used to represent an element or its atoms
- Dalton (Da)
- alternative unit equivalent to the atomic mass unit
- fundamental unit of charge
- (also called the elementary charge) equals the magnitude of the charge of an electron (e) with e = 1.602 \(\times\) 10−19 C
- ion
- electrically charged atom or molecule (contains unequal numbers of protons and electrons)
- mass number (A)
- sum of the numbers of neutrons and protons in the nucleus of an atom
- mole
- amount of substance containing the same number of atoms, molecules, ions, or other entities as the number of atoms in exactly 12 grams of 12C
- molar mass
- mass in grams of 1 mole of a substance
- unified atomic mass unit (u)
- alternative unit equivalent to the atomic mass unit
Contributors and Attributions
Paul Flowers (University of North Carolina - Pembroke), Klaus Theopold (University of Delaware) and Richard Langley (Stephen F. Austin State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at http://cnx.org/contents/85abf193-2bd...a7ac8df6@9.110).
- Adelaide Clark, Oregon Institute of Technology
- Fuse School, Open Educational Resource free of charge, under a Creative Commons License: Attribution-NonCommercial CC BY-NC (View License Deed: https://creativecommons.org/licenses/by-nc/4.0/)
- Crash Course Chemistry, Crash Course is a division of Complexly and videos are free to stream for educational purposes.
- TED-Ed’s commitment to creating lessons worth sharing is an extension of TED’s mission of spreading great ideas. Within TED-Ed’s growing library of TED-Ed animations, you will find carefully curated educational videos, many of which represent collaborations between talented educators and animators nominated through the TED-Ed website.

