3.2: Control of Enzymatic Activity
- Page ID
- 347414
A printable version of this section is here: BiochemFFA_4_2.pdf. The entire textbook is available for free from the authors at http://biochem.science.oregonstate.edu/content/biochemistry-free-and-easy
Regulation of enzyme activity
Apart from their ability to greatly speed the rates of chemical reactions in cells, enzymes have another property that makes them valuable. This property is that their activity can be regulated, allowing them to be activated and inactivated, as necessary. This is tremendously important in maintaining homeostasis, permitting cells to respond in controlled ways to changes in both internal and external conditions.
Inhibition of specific enzymes by drugs can also be medically useful. Understanding the mechanisms that control enzyme activity is, therefore, of considerable importance.
Inhibition
We will first discuss four types of enzyme inhibition – competitive, non-competitive, uncompetitive, and suicide inhibition. Of these, the first three types are reversible. The last one, suicide inhibition, is not.
Competitive inhibition
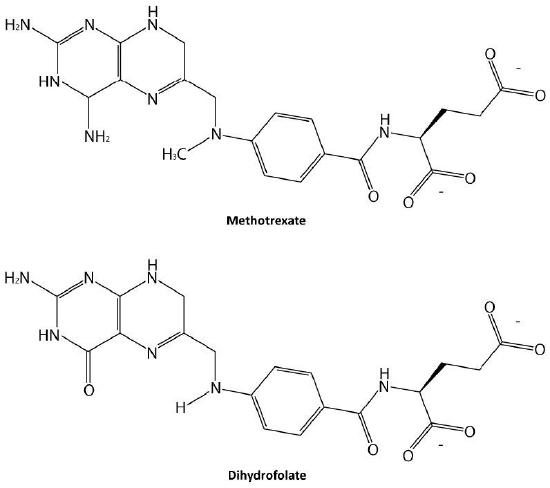
Probably the easiest type of enzyme inhibition to understand is competitive inhibition and it is the one most commonly exploited pharmaceutically. Molecules that are competitive inhibitors of enzymes resemble one of the normal substrates of an enzyme. An example is methotrexate, which resembles the folate substrate of the enzyme dihydrofolate reductase (DHFR). This enzyme normally catalyzes the reduction of folate, an important reaction in the metabolism of nucleotides.
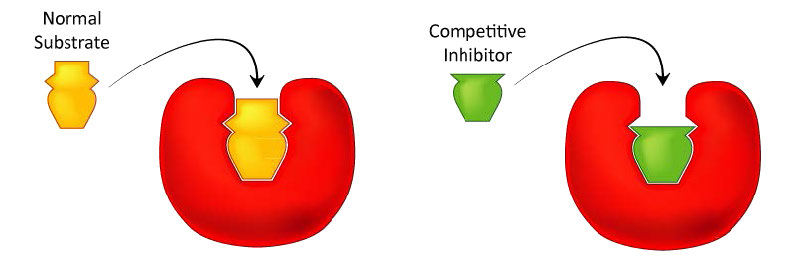
Figure 4.33 - Competitive inhibitors resemble the normal substrate and compete for binding at the active site. Image by Aleia Kim
Inhibitor binding
When the drug methotrexate is present, some of the DHFR enzyme binds to it, instead of to folate, and during the time methotrexate is bound, the enzyme is inactive and unable to bind folate. Thus, the enzyme is inhibited. Notably, the binding site on DHFR for methotrexate is the active site, the same place that folate would normally bind. As a result, methotrexate ‘competes’ with folate for binding to the enzyme. The more methotrexate there is, the more effectively it competes with folate for the enzyme’s active site. Conversely, the more folate there is, the less of an effect methotrexate has on the enzyme because folate outcompetes it.
No effect on Vmax
How do we study competitive inhibition? It is typically done as follows. First, one performs a set of V0 vs. [S] reactions without inhibitor (20 or so tubes, with buffer and constant amounts of enzyme, varying amounts of substrate, equal reaction times). V0 vs. [S] is plotted (Figure 4.35 red line), as well as 1/V0 vs. 1/[S] (Figure 4.36 green line). Next, a second set of reactions is performed in the same manner as before, except that a fixed amount of the methotrexate inhibitor is added to each tube. At low concentrations of substrate, the methotrexate competes for the enzyme effectively, but at high concentrations of substrate, the inhibitor will have a much reduced effect, since the substrate outcompetes it, due to its higher concentration (remember that the inhibitor is at fixed concentration).
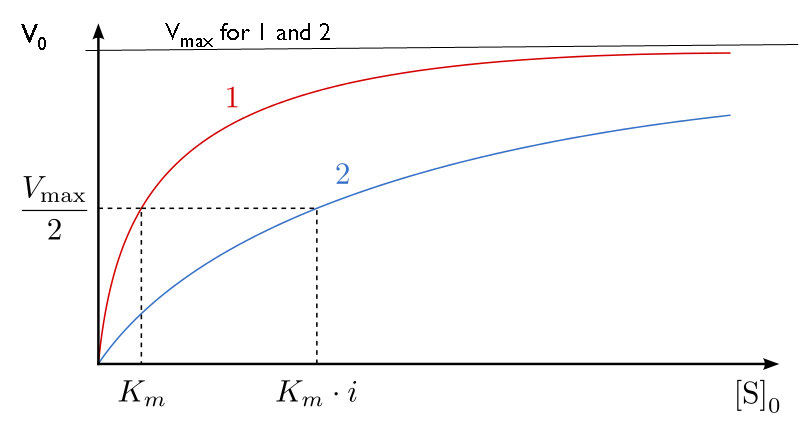
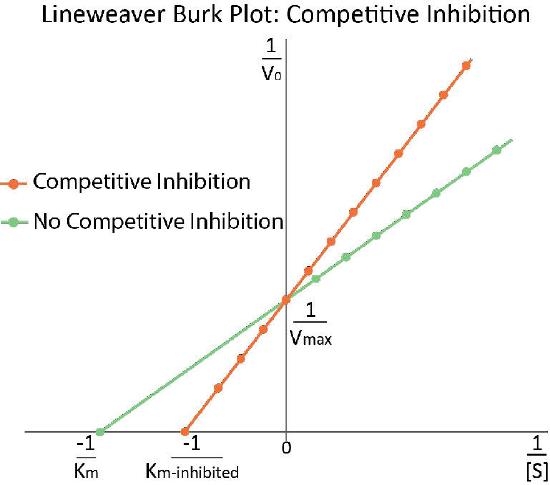
Graphically, the results of these inhibitor experiments are shown in Figure 4.35 (blue line) and Figure 4.36 (orange line). Notice that at high substrate concentrations, the competitive inhibitor has essentially no effect, causing the \(V_{max}\) for the enzyme to remain unchanged. To reiterate, this is due to the fact that at high substrate concentrations, the inhibitor doesn’t compete well. However, at lower substrate concentrations, it does.
Increased \(K_m\)
In competitively inhibited reactions, the apparent Km of the enzyme for the substrate increases (\(-1/K_m\) gets closer to zero - red line in Figure 4.36) when the inhibitor is present compared to when the inhibitor is absent, thus illustrating the better competition of the inhibitor at lower substrate concentrations. It may not be obvious why we call the changed Km the apparent Km of the enzyme. The reason is that the inhibitor doesn’t actually change the enzyme’s affinity for the folate substrate. It only appears to do so. This is because of the way that competitive inhibition works. When the competitive inhibitor binds the enzyme, it is effectively ‘taken out of action.’ Inactive enzymes have NO affinity for substrate and no activity either. We can’t measure Km for an inactive enzyme.
The enzyme molecules that are not bound by methotrexate can, in fact, bind folate and are active. Methotrexate has no effect on them and their Km values are unchanged. Why then, does Km appear higher in the presence of a competitive inhibitor? The reason is that the competitive inhibitor is having a greater effect of reducing the amount of active enzyme at lower concentrations of substrate than it does at higher concentrations of substrate. When the amount of enzyme is reduced, one must have more substrate to supply the reduced amount of enzyme sufficiently to get to Vmax/2.
It is worth noting that in competitive inhibition, the percentage of inactive enzyme changes drastically over the range of [S] values used. To start, at low [S] values, the greatest percentage of the enzyme is inhibited. At high [S], no significant percentage of enzyme is inhibited. This is not always the case, as we shall see in non-competitive inhibition.
Non-competitive inhibition
A second type of inhibition employs inhibitors that do not resemble the substrate and bind not to the active site, but rather to a separate site on the enzyme (Figure 4.37). The effect of binding a non-competitive inhibitor is significantly different from binding a competitive inhibitor because there is no competition. In the case of competitive inhibition, the effect of the inhibitor could be reduced and eventually overwhelmed with increasing amounts of substrate. This was because increasing substrate made increasing percentages of the enzyme active. With non-competitive inhibition, increasing the amount of substrate has no effect on the percentage of enzyme that is active. Indeed, in non-competitive inhibition, the percentage of enzyme inhibited remains the same through all ranges of [S].
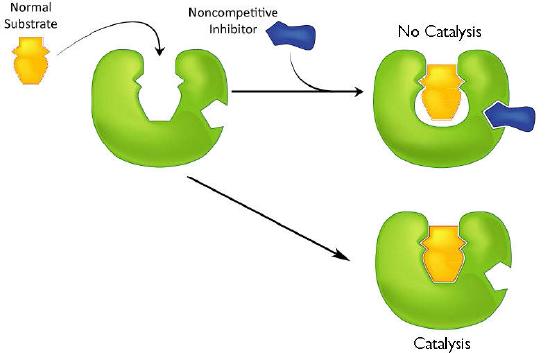
This means, then, that non-competitive inhibition effectively reduces the amount of enzyme by the same fixed amount in a typical experiment at every substrate concentration used The effect of this inhibition is shown in Figure 4.38 & 4.39. As you can see, \(V_{max}\) is reduced in non-competitive inhibition compared to uninhibited reactions.
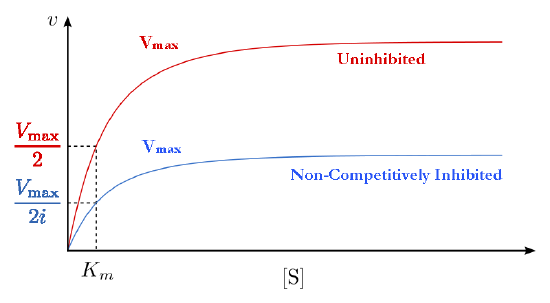
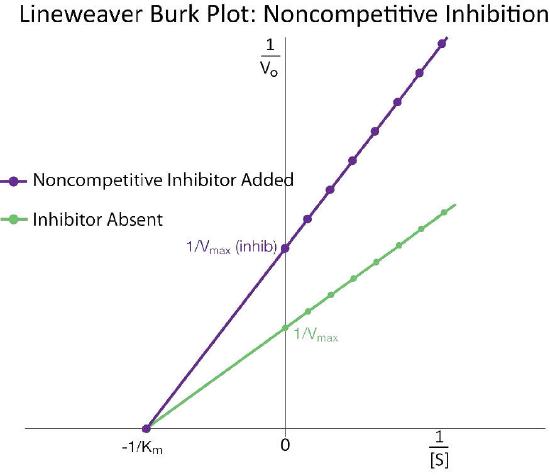
This makes sense if we remember that Vmax is dependent on the amount of enzyme present. Reducing the amount of enzyme present reduces \(V_{max}\). In competitive inhibition, this doesn’t occur detectably, because at high substrate concentrations, there is essentially 100% of the enzyme active and the \(V_{max}\) appears not to change. Additionally, Km for non-competitively inhibited reactions does not change from that of uninhibited reactions. This is because, as noted previously, one can only measure the \(K_m\) of active enzymes and \(K_m\) is a constant for a given enzyme.
Uncompetitive inhibition
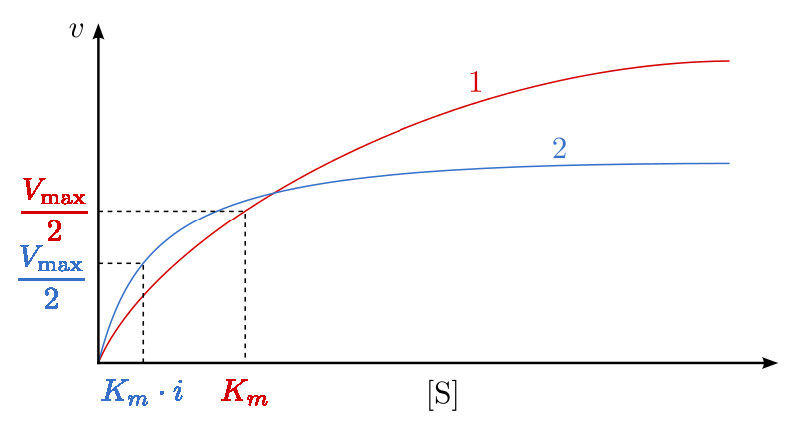
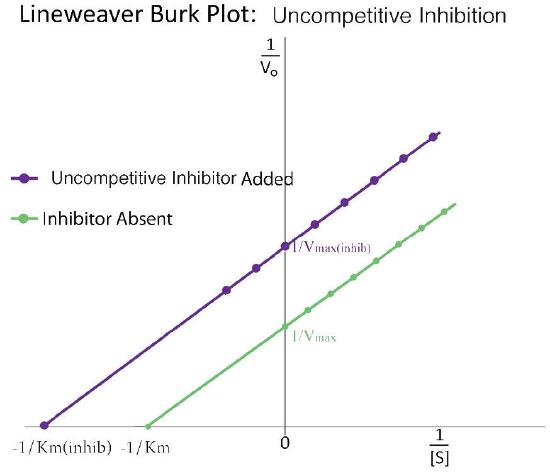
A third type of enzymatic inhibition is that of uncompetitive inhibition, which has the odd property of a reduced Vmax as well as a reduced Km. The explanation for these seemingly odd results is rooted in the fact that the uncompetitive inhibitor binds only to the enzyme-substrate (ES) complex (Figure 4.40). The inhibitor-bound complex forms mostly under concentrations of high substrate and the ES-I complex cannot release product while the inhibitor is bound, thus explaining the reduced \(V_{max}\).
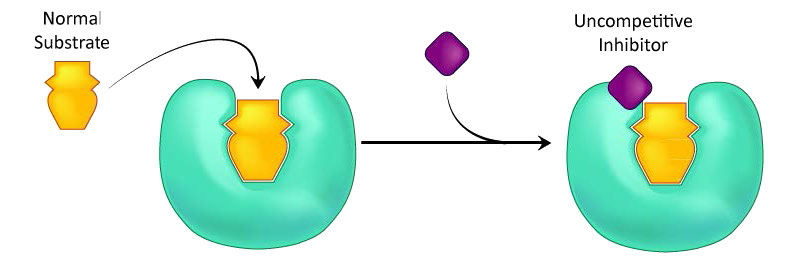
The reduced Km is a bit harder to conceptualize. The reason is that the inhibitor-bound complex effectively reduces the concentration of the ES complex. By Le Chatelier’s Principle, a shift occurs to form additional ES complex, resulting in less free enzyme and more enzyme in the forms ES and ESI (ES with inhibitor). Decreases in free enzyme correspond to an enzyme with greater affinity for its substrate. Thus, paradoxically, uncompetitive inhibition both decreases \(V_{max}\) and increases an enzyme’s affinity for its substrate (\(K_m\) - Figures 4.41 & 4.42).
Irreversible (Suicide) inhibition
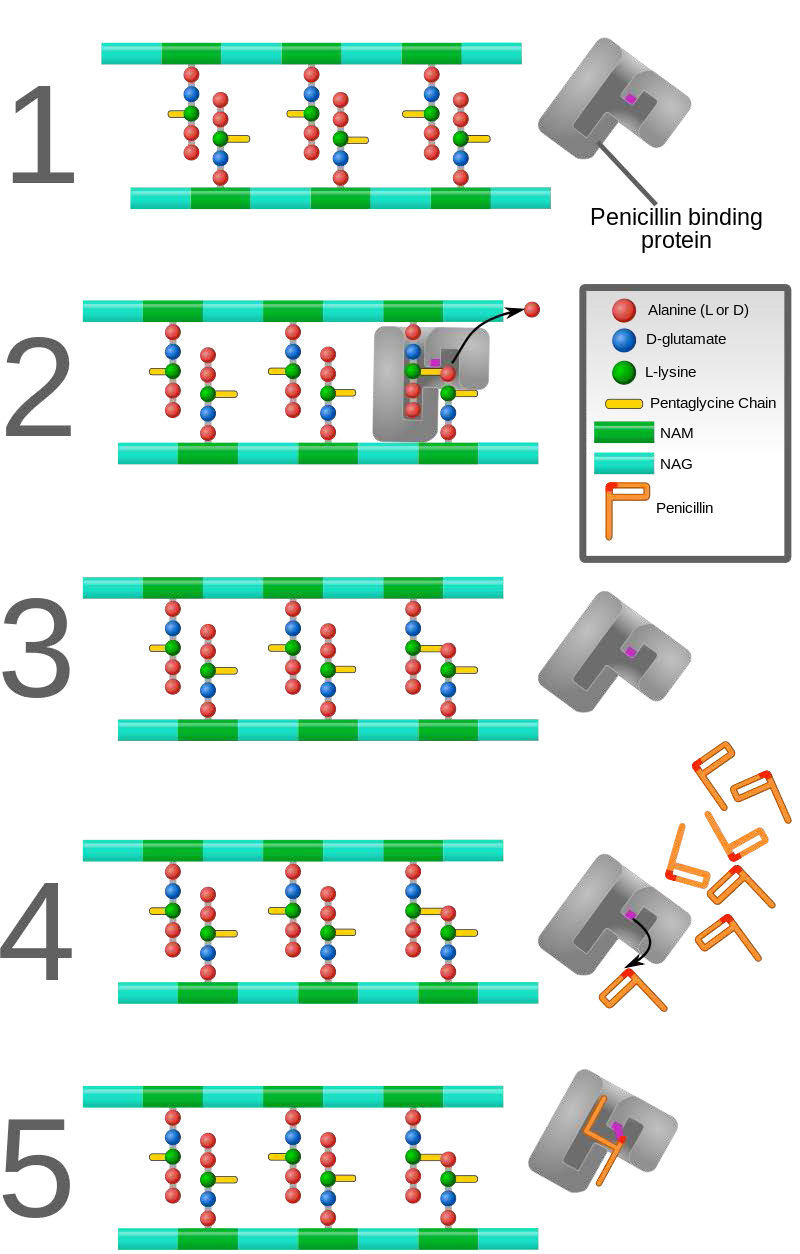
In contrast to the first three types of inhibition, which involve reversible binding of the inhibitor to the enzyme, suicide inhibition is irreversible, because the inhibitor becomes covalently bound to the enzyme during the inhibition. Suicide inhibition rather closely resembles competitive inhibition because the inhibitor generally resembles the substrate and binds to the active site of the enzyme. The primary difference is that the suicide inhibitor is chemically reactive in the active site and makes a bond with it that precludes its removal. Such a mechanism is that employed by penicillin (Figure 4.43), which covalently links to the bacterial enzyme, DD transpeptidase and stops it from functioning. Since the normal function of the enzyme is to make a bond necessary for the peptidoglycan complex of the bacterial cell wall, the cell wall cannot properly form and bacteria cannot reproduce.
Control of enzymes
It is appropriate to talk at this point about mechanisms cells use to control enzymes. There are four general methods that are employed:
- allosteric regulation,
- covalent modification,
- access to substrate, and
- control of enzyme level via synthesis or breakdown.
Some enzymes are controlled by more than one of these methods.
Allosteric regulation
The term allosteric regulation, or allostersim, refers to the fact that the activity of certain enzymes can be affected by the binding of small molecules. Molecules causing allosteric effects come in two classifications. A substrate for an enzyme can also regulate that same enzyme. These allosteric regulators are generally called homotropic effectors. Regulators that are not substrates are called heterotropic effectors.
The homotropic effectors usually are activators of the enzymes they bind to and the results of their action can be seen in the conversion of the hyperbolic curve typical of a V0 vs. [S] plot for an enzyme (Figure 4.18), being converted to a sigmoidal plot (Figure 4.44). This is due to the conversion of the enzyme from the T-state to the R-state on binding the substrate/homotropic effector.
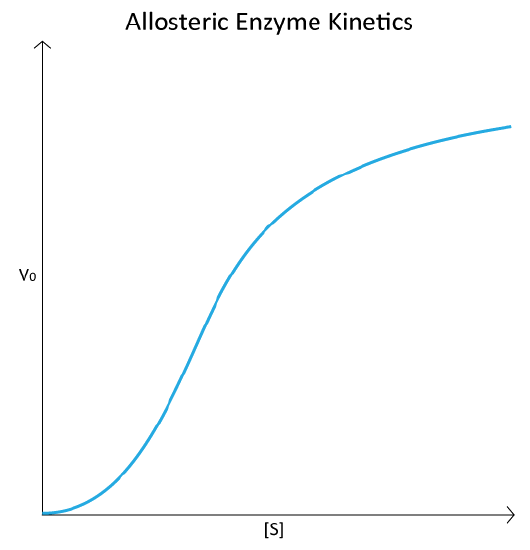
The V0 vs. [S] plot of allosteric enzyme reactions resembles the oxygen binding curve of hemoglobin (see Figure 2.83). Even though hemoglobin is not an enzyme and is thus not catalyzing a reaction, the similarity of the plots is not coincidental. In both cases, the binding of an external molecule is being measured – directly, in the hemoglobin plot, and indirectly by the V0 vs. [S] plot, since substrate binding is a factor in enzyme reaction velocity.
Allosteric inhibition
Allosterically, regulation of these enzymes works by inducing different physical states (shapes, as it were) that affect their ability to bind to substrate. When an enzyme is inhibited by binding an effector, it is converted to the T-state (T=tight), it has a reduced affinity for substrate and it is through this means that the reaction is slowed.
Allosteric activation
On the other hand, when an enzyme is activated by effector binding, it converts to the R-state (R=relaxed) and binds substrate much more readily. When no effector is present, the enzyme may be in a mixture of T- and R-states.
Feedback inhibition
An interesting kind of allosteric control is exhibited by HMG-CoA reductase, which catalyzes an important reaction in the pathway leading to the synthesis of cholesterol. Binding of cholesterol to the enzyme reduces the enzyme’s activity significantly. Cholesterol is not a substrate for the enzyme, so it is therefore a heterotropic effector.
Notably, though, cholesterol is the end-product of the pathway that HMG-CoA reductase catalyzes a reaction in. When enzymes are inhibited by an end-product of the pathway in which they participate, they are said to exhibit feedback inhibition.
Feedback inhibition always operates by allosterism and further, provides important and efficient control of an entire pathway. By inhibiting an early enzyme in a pathway, the flow of materials (and ATP hydrolysis required for their processing) for the entire pathway is stopped or reduced, assuming there are not alternate supply methods.
Pathway control
In the cholesterol biosynthesis pathway, stopping this one enzyme has the effect of shutting off (or at least slowing down) the entire pathway. This is significant because after catalysis by HMG-CoA reductase, there are over 20 further reactions necessary to make cholesterol, many of them requiring ATP energy. Shutting down one reactions stops all of them. Another excellent example of allosteric control and feedback inhibition is the enzyme ATCase, discussed below.
ATCase
Another interesting example of allosteric control and feedback inhibition is associated with the enzyme Aspartate Transcarbamoylase (ATCase). This enzyme, which catalyzes a step in the synthesis of pyrimidine nucleotides, has 12 subunits. These include six identical catalytic subunits and six identical regulatory subunits. The catalytic subunits bind to substrate and catalyze a reaction. The regulatory subunits bind to either ATP or CTP. If they bind to ATP, the enzyme subunits arrange themselves in the R-state.
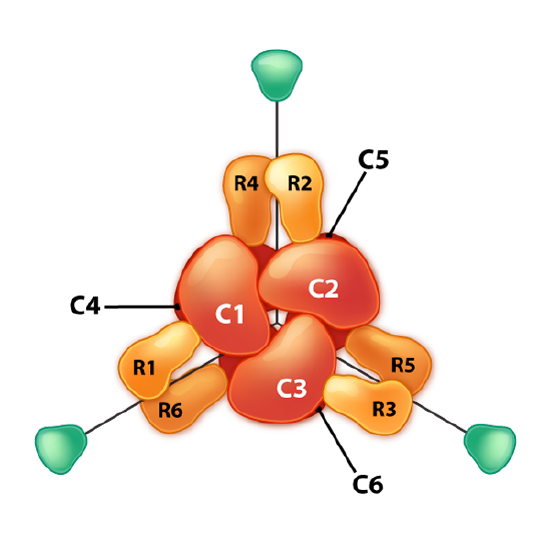
R-state
The R-state of ATCase allows the substrate to have easier access to the six active sites and the reaction occurs more rapidly. For the same amount of substrate, an enzyme in the R-state will have a higher velocity than the same enzyme that is not in the R-state. By contrast, if the enzyme binds to CTP on one of its regulatory subunits, the subunits will arrange in the T-state and in this form, the substrate will not have easy access to the active sites, resulting in a slower velocity for the same concentration of substrate compared to the R-state. ATCase is interesting in that it can also flip into the R-state when one of the substrates (aspartate) binds to an active site within one of the catalytic subunits.
Aspartate has the effect of activating the catalytic action of the enzyme by favoring the R-state. Thus, aspartate, which is a substrate of the enzyme is a homotropic effector and ATP and CTP, which are not substrates of the enzyme are heterotropic effectors of ATCase.
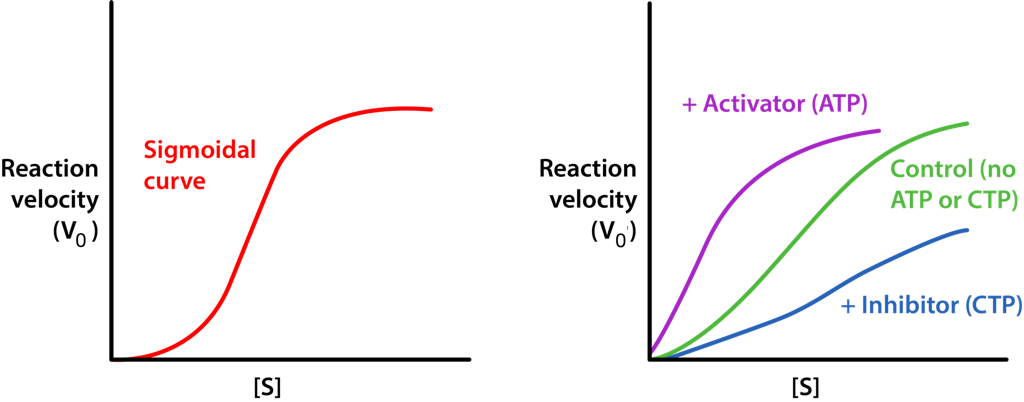
Optional: Allosteric models
There are three models commonly used to explain how allosterism regulates multi-subunit enzyme activity. They are known as
- the Monod-Wyman-Changeux (MWC) model (also known as the concerted model),
- the sequential model (also known as KNF),
- and the morpheein model.
All models describe a Tense (T) state that is less catalytically active and a Relaxed (R) state that is more catalytically active. The models differ in how the states change.
Sequential model
In the sequential model, binding of an allosteric effector by one subunit causes it to change from T to R state (or vice versa) and that change makes it easier for adjacent subunits to similarly change state. With this model , there is a cause/effect relationship between binding of an effector by one subunit and change of state by an adjacent subunit.
In hemoglobin, for example, binding of one oxygen by one unit of the complex may induce that unit to flip to the R-state and, through interactions with other subunits, cause them to favor adopting the R configuration before they bind to oxygen. In this way, binding of one subunit favors binding of others and cooperativity can be explained by the change in binding affinity as oxygen concentration changes.

MWC model
The MWC model is less intuitive. In it, the entire complex changes state from T to R (or vice versa) independently of the binding of effectors. Flipping between T-states and R-states is postulated to be in an equilibrium of states in the absence of effector (for example, a 50 to 1 ratio of T/R. This ratio is referred to as L, so L = T/R). Binding of effector by the enzyme complex has the tendency of “locking” the complex in a state. Binding of inhibitors will increase the ratio of T/R whereas binding of activators will increase R and thus decrease the ration of T/R.
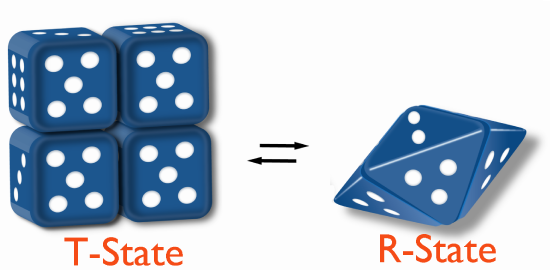
Morpheein model
The morpheein model is similar to the MWC model, but with an added step of dissociation of the subunits. The MWC model proposes that flipping between R and T states occurs by the complex as a whole and occurs on all units simultaneously. The morpheein model instead proposes that the multi-subunit enzyme breaks down to individual units which can then flip in structure and re-form the complex. In the morpheein model, only identically shaped units (all R, for example) can come together in the complex, thus explaining the “all-R-” or “all-T-” state found in the MWC model.
A large number of enzymes, including prominent ones like citrate synthase, acetyl-CoA carboxylase, glutamate dehydrogenase, ribonucleotide reductase and lactate dehydrogenase have behavior consistent with the morpheein model.

Covalent control of enzymes
Some enzymes are synthesized in a completely inactive form and their activation requires covalent bonds in them to be cleaved. Such inactive forms of enzymes are called zymogens. Examples include the proteins involved in blood clotting and proteolytic enzymes of the digestive system, such as trypsin, chymotrypsin, pepsin, and others.
Synthesizing some enzymes in an inactive form makes very good sense when an enzyme’s activity might be harmful to the tissue where it is being made. For example, the painful condition known as pancreatitis arises when digestive enzymes made in the pancreas are activated too soon and end up attacking the pancreas.
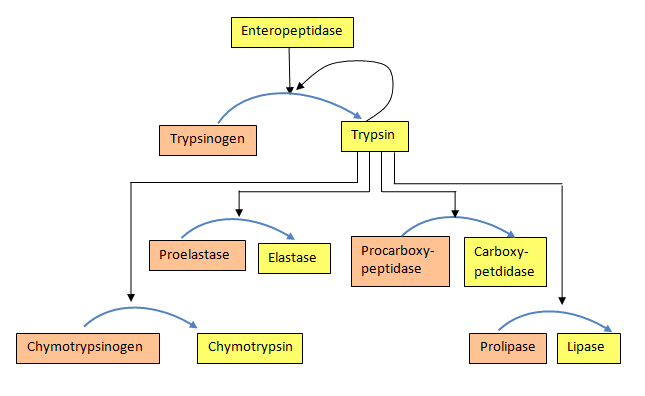
Cascades
For both the blood clotting enzymes and the digestive enzymes, the zymogens are activated in a protease cascade. This occurs when activation of one enzyme activates others in a sort of chain reaction. In such a scheme the first enzyme activated proteolytically cleaves the second zymogen, causing it to be activated, which in turn activates a third and this may proceed through several levels of enzymatic action (Figure 4.50).
The advantage of cascades is that they allow a large amount of zymogens to become activated fairly quickly, since there is an amplification of the signal at each level of catalysis.
Zymogens are also abundant in blood. Blood clotting involves polymerization of a protein known as fibrin. Since random formation of fibrin is extremely hazardous because it can block the flow of blood, potentially causing heart attack/stroke, the body synthesizes fibrin as a zymogen (fibrinogen) and its activation results from a “cascade” of activations of proteases that arise when a signal is received from a wound. Similarly, the enzyme catalyzing removal of fibrin clots (plasmin) is also synthesized as a zymogen (plasminogen), since random clot removal would also be hazardous (see below also).
Phosphorylation/dephosphorylation
Another common mechanism for control of enzyme activity by covalent modification is phosphorylation. The phosphorylation of enzymes (on the side chains of serine, threonine or tyrosine residues) is carried out by protein kinases. Enzymes activated by phosphorylation can be regulated by the addition of phosphate groups by kinases or their removal by phosphatases. Thus, this type of covalent modification is readily reversible, in contrast to proteolytic cleavage.
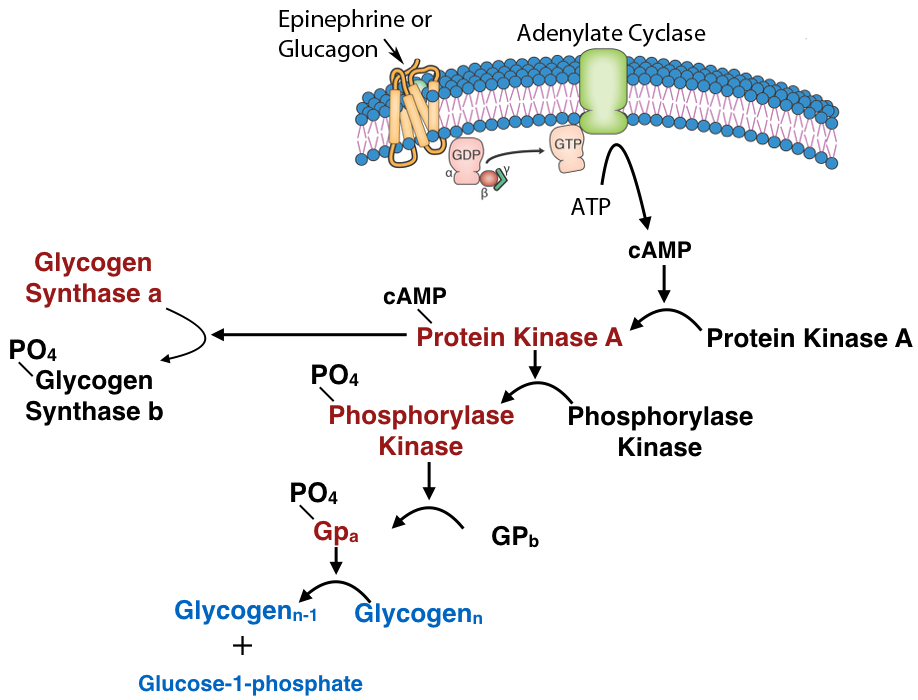
Reduction/oxidation
An interesting covalent control of enzymes using reduction/oxidation is exhibited in photosynthetic plants. In the light phase of photosynthesis, electrons are excited by light and flow through carriers to NADP+, forming NADPH. Thus, in the light, the NADPH concentration is high. When NADPH concentration is high, the concentration of reduced ferredoxin (a molecule donating electrons to NADP+) is also high.
Reduced ferredoxin can transfer electrons to thioredoxin, reducing it. Reduced thioredoxin can, in turn, transfer electrons to proteins to reduce their disulfide bonds. Four enzymes related to the Calvin cycle can receive electrons from thioredoxin and become activated, as a result.
These include sedoheptulose 1,7-bisphosphatase, ribulose-5-phosphate kinase, fructose 1,6-bisphosphatase, and glyceraldehyde 3-phosphate dehydrogenase. Thus, in the light, electrons flow, causing NADPH to accumulate and ferredoxin to push electrons in the direction of these enzymes above, activating them and favoring the Calvin cycle. In the dark, the concentration of reduced NADPH, reduced ferredoxin, and reduced thioredoxin fall, resulting in loss of electrons by the Calvin cycle enzymes (oxidations that re-form disulfide bonds) and the Calvin cycle inactivates.
Other enzyme control mechanisms
Other means of controlling enzymes relate to access to the substrate (substrate-level control) and control of enzyme synthesis. Hexokinase is an enzyme that is largely regulated by the availability of its substrate, glucose. When glucose concentration is low, the product of the enzyme’s catalysis, glucose-6-phosphate, inhibits the enzyme’s function.
Regulation of enzymes by controlling their synthesis is covered later in the book in the discussion relating to control of gene expression.


