In ccp and hcp lattices, there are two tetrahedral holes per packing atom. A stoichiometry of either M2X or MX2 gives a structure that fills all tetrahedral sites, while an MX structure fills only half of the sites. An example of an MX2 structure is fluorite, CaF2, whose structure is shown in the figure at the left. The packing atom in fluorite is Ca2+ and the structure is composed of three interpenetrating fcc lattices. It should be noted that the Ca2+ ion (gray spheres) as a packing atom defies our "rule" that anions are larger than cations and therefore must be the packing atoms. The fluorite structure is common for ionic MX2 (MgF2, ZrO2, etc.) and M2X compounds (Li2O). In contrast, the hcp relative of the fluorite structure is quite rare because of unfavorable close contacts between like-charged ions.
|
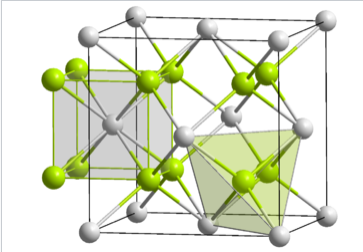
The fluorite (CaF2) crystal structure showing the coordination environments of the Ca and F atoms
|
In terms of geometry, Ca2+ is in cubic coordination with eight F- neighbors, and the fluoride ions are tetrahedrally coordinated by four Ca2+ ions. The 8:4 coordination geometry is consistent with the 1:2 Ca:F stoichiometry; in all crystal structures the ratio of the coordination numbers is the inverse of the stoichiometric ratio. The three interpenetrating fcc lattices have Ca at 0,0,0 , 1/2,1/2,0 , etc....F at 1/4,1/4,1/4 , 3/4,3/4,1/4 , etc... and F at 3/4,3/4,3/4 , 1/4,1/4/3/4 , etc.
Looking more closely at the tetrahedral sites in fluorite, we see that they fall into two distinct groups: T+ and T-. If a tetrahedron is oriented with a vertex pointing upwards along the stacking axis, the site is T+. Likewise, a tetrahedron with a vertex oriented downward is T-. The alternation of T+ and T- sites allows for efficient packing of ions in the structure. The layer stacking sequence in this structure (including fluoride ions in the T+ and T- sites) is:
- ------------ A
- - - -b- - - T+
- - - -a- - - T-
- ------------ B
- - - -c- - - T+
- - - -b- - - T-
- ------------ C
- - - -a- - - T+
- - - -c- - - T-
- ------------ A
- - - -b- - - T+
- - - -a- - - T-
|

Polyhedral view of the fluorite crystal structure, showing T+ and T- Ca4F tetrahedra. The Ca2+ ions are stacked ABCABC... along the body diagonal of the unit cell, which is the vertical direction in this image.
|
Tetrahedrally bonded compounds with a 1:1 stoichiometry (MX compounds) have only half of the tetrahedral sites (either the T+ or T- sites) filled. In this case, both the M and the X atoms are tetrahedrally coordinated. The zincblende and wurtzite structures are 1:1 tetrahedral structures based on fcc and hcp lattices, respectively. Both structures are favored by p-block compounds that follow the octet rule, and these compounds are usually semiconductors or insulators. The zincblende structure, shown below, can be thought of as two interpenetrating fcc lattices, one of anions and one of cations, offset from each other by a translation of 1/4 along the body diagonal of the unit cell. Examples of compounds with the zincblende structure include CuCl, CuI, ZnSe, HgS, BeS, CdTe, AlP, GaP, SnSb, CSi, and diamond. Additionally, the compound CuInSe2 is zincblende in an ordered, doubled unit cell (the chalcopyrite structure). The solid solution compounds CuIn1-xGaxSe2 with this structure are among the most widely studied materials for use in efficient thin film photovoltaic cells. Using ZnS as a representative of zincblende, the coordination of both Zn and S atoms is tetrahedral. The layer sequence, which is AbBcCaAbBcC..., results in six-membered ZnS rings that have the same geometry as the "chair" version of cyclohexane. The chair conformation allows for a relatively long distance between opposite atoms in the ring and, as a result, it is more sterically favorable than the boat form. The sequence of close-packed layers in zincblende, filling only the T+ sites and leaving the T- sites empty, is shown below:
- ------------ A
- - - -b- - - T+
- - - - - - - T-
- ------------ B
- - - -c- - - T+
- - - - - - - T-
- ------------ C
- - - -a- - - T+
- - - - - - - T-
|
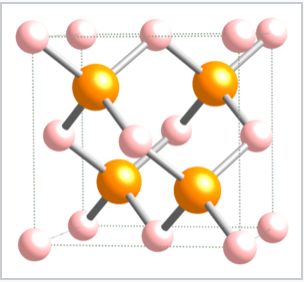
The zincblende unit cell
|
The wurtzite structure is a close relative of zinc blende, based on filling half the tetrahedral holes in the hcp lattice. Like zincblende, wurtzite contains planes of fused six-membered rings in the chair conformation. Unlike zincblende, however, the rings joining these planes contain six-membered "boat" rings. The boat aligns the anions so that they are directly above the cations in the structure, a less favorable situation sterically but a more favorable one in terms of electrostatics. As a result, the wurtzite structure tends to favor more polar or ionic compounds (e.g., ZnO, NH4+F-) than the zincblende structure. As with zincblende, both ions are in tetrahedral (4:4) coordination and there are typically eight valence electrons in the MX compound. Examples of compounds with this structure include: BeO, ZnO, MnS, CdSe, MgTe, AlN, and NH4F. The layered structure of wurtzite is AbBaAbB and the layer sequence with T+ sites filled is illustrated below:
- ------------ A
- - - -b- - - T+
- - - - - - - T-
- ------------ B
- - - -a- - - T+
- - - - - - - T-
- ------------ A
- - - -b- - - T+
- - - - - - - T-
- ------------ B
|
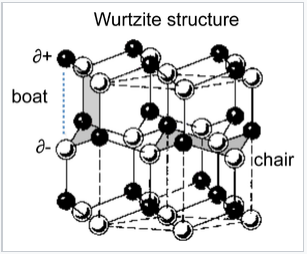
The chair and boat conformations of six-membered ZnS rings in the wurtzite structure.
|
An interesting consequence of the layer stacking in the wurtzite structure is that the crystals are polar. When cleaved along the c-axis (the stacking axis), crystals of ZnO, ZnS, and GaN have one negatively charged face and an opposite positively charged face. An applied electric field interacts with the crystal dipole, resulting in compression or elongation of the lattice along this direction. For this reason crystals of compounds in the wurtzite structure are typically piezoelectric.
Some compounds are diamorphic and can have either the zincblende or wurtzite structure. Examples of these compounds that have intermediate polarities include CdS and ZnS. SiO2 exists in polymorphs (crystobalite and tridymite) that resemble zincblende and wurtzite with O atoms midway between each of the Si atoms. The zincblende and wurtzite structures have efficient packing arrangements for tetrahedrally bonded networks and are commonly found in compounds that have tetrahedral bonding. Water, for example, has a tetrahedral hydrogen bonding network and is wurtzite-type. The undistorted wurtzite and zinc blende structures are typically found for AX compounds with eight valence electrons, which follow the octet rule. AX compounds with nine or ten electrons such as GaSe and GaAs crystallize in distorted variants of the wurtzite structure. In GaSe, the extra electrons form lone pairs and this creates layers in the structure, as can be seen in the figure below. To the right of GaSe, the structures of As, Sb, and SbAs show an ever further breakdown of the structure into layers as more valence electrons are added.
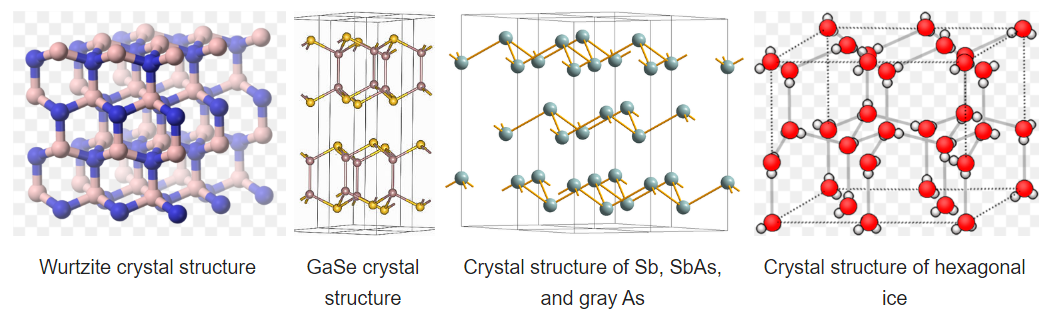
Hexagonal ice is the most stable polymorph of ice, which is obtained upon freezing at 1 atmosphere pressure. This polymorph (ice-I) has a hcp wurtzite-type structure. Looking at the structure shown at the right, we see that there are irregular arrangements of the O-H---O bonds. In the structure, hydrogen bonding enforces the tetrahedral coordination of each water molecule, resulting in a relatively open structure that is less dense than liquid water. For this reason, ice floats in water.






