2.3: Matrix Representations of Symmetry Operations and Character Tables
- Last updated
- Save as PDF
- Page ID
- 344575
Matrix Representations of Symmetry Operations
Thus, far we have looked at symmetry operations qualitatively, and determined their nature by inspection. Now let us have a look how we can describe symmetry operations from a more mathematical point of view. Why do we do this? We do this to be able to understand so-called character tables which we will later need to apply symmetry to molecular orbital theory. Generally, symmetry operations can be described by matrices. When a matrix representing a symmetry operation is multiplied with coordinates of an object, then this gives the new coordinates of the object after the symmetry operation was carried out. Therefore let us briefly review matrices, and matrix multiplications in particular. A matrix is nothing but an array of numbers arranged into rows and columns. When we multiply to matrices, we must multiply each row with each column of the matrix. When the first matrix Aik has i rows and k columns and the second matrix Bkj has k rows and j columns, then the product matrix Cij has i rows and j columns. A requirement for a matrix multiplication is that the number of columns of the first matrix is the same as the number of the rows of the second column. Otherwise, one can just not multiply each row with each column of the two matrices.
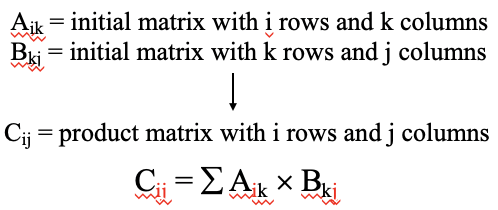
Let us do this by a few examples.
Example 1 of Matrix Multiplication
In the first example we multiply two 2x2 matrices, meaning that they both have two rows and two columns (Fig. 2.3.2). First, we need to check if the two matrices can be multiplied. We can see that the number columns of the first matrix is 2, and the number of rows of the second matrix is also 2. Therefore, we can multiply the two matrices.
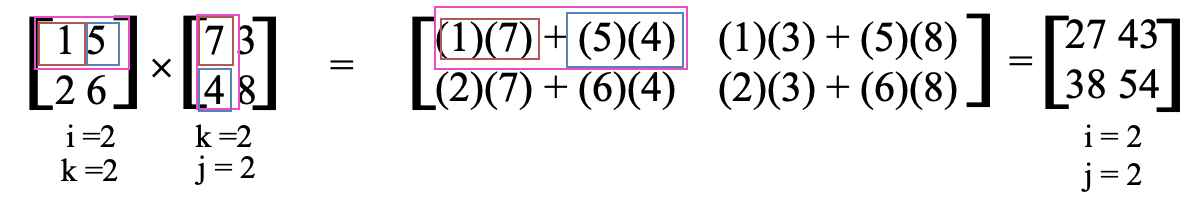
The product matrix is expected to be also a 2x2 matrix. Now we need to multiply the first row of the first matrix with the first column of the second matrix, and that means that we to multiply 1x7 and 5x4. The sum of 1x7+5x4=27 gives us the first character of the first row of the product matrix. Next, we multiply the first row of the first matrix with the second column of the second matrix. So we have to multiply 1x3 and 5x8. The sum of the two products gives the second character of the first row of the product matrix. Because the second matrix has no additional column, there is no further column with which the first row of the first matrix could be multiplied. Therefore, we now go to the second row of the first matrix, and multiply it with the first column of the second matrix. This gives the products 2x7 and 6x4. When added together, then this gives 38, and this is now the first character of the second row of the product matrix. Lastly, we multiply the second row of the first matrix with the second row of the second matrix. This gives 2x3 and 6x8 which gives 54 when added together. This is the second character in the second row of the product matrix.
Example 2 of Matrix Multiplication
In the next example, we multiply a 1x3 matrix with a 3x3 matrix (Fig. 2.3.3). This is possible because the number of the columns of the second matrix is 3, and the number of rows of the second matrix is also 3.
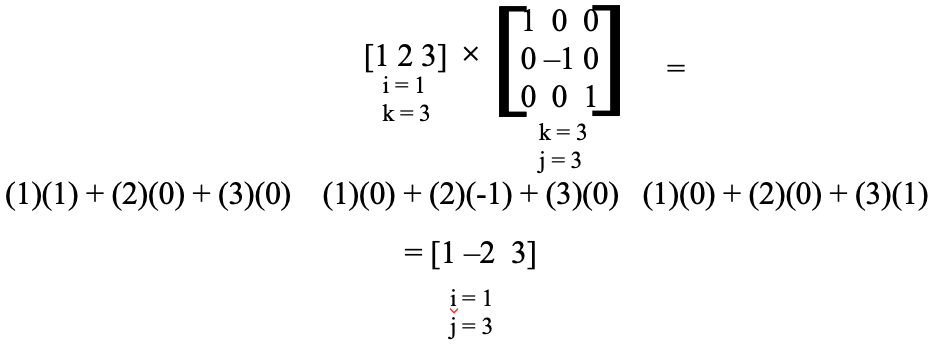
The product matrix would be expected to have one row and three columns. The first matrix has only one row, so we multiply it with the three columns of the second matrix. Multiplying the first row of the first matrix with the first column of the second matrix gives (1)(1) + (2)(0) + (3)(0) = 1. This is the first character in the first, and only row in the product matrix. The multiplication of the first row of the first matrix with the second column of the second matrix is (1)(0) + (2)(-1) + (3)(0) = -2 which is the second character of the first row of the product matrix. The multiplication of the first row of the first matrix with the third column of the second matrix gives (1)(0) + (2)(0) + (3)(1) = 3. This is the third character of the first row of the product matrix. Overall, the product matrix is [1 -2 3].
Example 3 of Matrix Multiplication
In the last example let us multiply a 3x3 matrix with a 3x1 matrix (Fig. 2.3.4). Again, the number of the columns of the first matrix is the same as the number of the rows of the second matrix, they are both 3. Thus, we can multiply the two matrices.
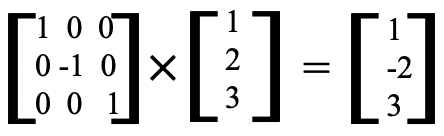
Multiplying the first row of the first matrix with the first, and in this case only column of the second matrix gives 1x1 + 0x2 + 0x3 = 1. This is the first and only character of the first row of the product matrix. The second matrix has only one column, therefore we multiply the second row of the first matrix with the only column of the second matrix in the next step. This gives 0x1 + (-1)x2 + 0x3 = -2. This the character of the second row of the product matrix. Lastly, we multiply the third row of the first matrix with the column of the second matrix. This gives 0x1 + 0x2 + 1x3 = 3. This is the character of the third row of the product matrix.
Applying Matrix Multiplications to Symmetry Operations
So what do symmetry operations have to do with the multiplication of matrices? The answer is that a symmetry operation can be described as a matrix, and the multiplication of this matrix with the matrix that represents the coordinates of the position of the points in an object, will give the new coordinates of the object after the symmetry operation has been carried out (Fig. 2.3.5).

Example H2O
A matrix that represents a symmetry operation is a 3x3 matrix and the matrix that describes coordinates is a 3x1 matrix. When two are multiplied then this gives a 3x1 matrix that describes the new coordinates of the object. For example, let us look at the water molecule H2O.
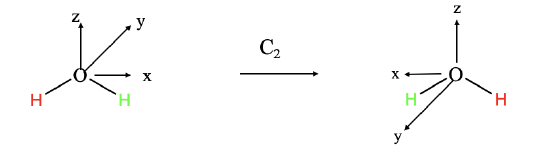
We can define a coordinate system in the water molecule so that the molecule is within the xz plane, whereby the z-axis is chosen so that it bisects the H-O-H bond angle. The y-axis would stand perpendicular and point into the board plane (Fig. 2.3.6). Any point within the water molecule, would have coordinates x,y,z that are defined by vectors 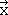 ,
,  ,
, 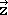 that point to these coordinates. For example, the center of a particular hydrogen atoms would have specific coordinates that would be described by three vectors that when added up, would point to the center of the hydrogen atom. Now let us think how the coordinates will change as we carry out a specific symmetry operations. For instance, take the C2 symmetry operation that is carried out around the z-axis. How will the rotation change, the x,y, and z coordinates, respectively?
that point to these coordinates. For example, the center of a particular hydrogen atoms would have specific coordinates that would be described by three vectors that when added up, would point to the center of the hydrogen atom. Now let us think how the coordinates will change as we carry out a specific symmetry operations. For instance, take the C2 symmetry operation that is carried out around the z-axis. How will the rotation change, the x,y, and z coordinates, respectively?
The x-coordinate is defined by a vector pointing into x-direction. As we rotate this vector 180° around the z-axis, it will retain its length but will point into the opposite direction (Fig. 2.3.6). Hence, we can say that the coordinate x has changed its algebraic sign, and is now –x. Now what about the y-coordinate? A vector pointing into y-direction will also be rotated around 180°, and point into the opposite direction. That means it is –y after the execution of the symmetry operation. Finally, how will the z-coordinate change? Because we rotate around z, there will not be any change to the z-vector, and thus the new coordinate z will be identical to the old coordinate z. If we represent the three vectors of the old coordinates by a 3x1 matrix 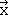 ,
, 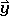 ,
, 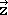 , the new coordinates of the matrix
, the new coordinates of the matrix  ',
', 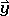 ',
', 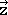 ' are represented by the matrix -
' are represented by the matrix -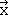 ,-
,- 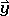 ,
, 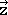 . The matrix that when multiplied with the matrix for the old coordinates gives the matrix for the new coordinates, would be the matrix that would represent the symmetry operation C2. In the case of the C2 symmetry operation the matrix has the form below (Fig. 2.3.7).
. The matrix that when multiplied with the matrix for the old coordinates gives the matrix for the new coordinates, would be the matrix that would represent the symmetry operation C2. In the case of the C2 symmetry operation the matrix has the form below (Fig. 2.3.7).

We can show that this matrix correctly represents the symmetry operation C2 by applying the multiplication rules for matrices. Multiplying the first row of the matrix for C2 with the only column of the matrix for the old coordinates would give (-1 x 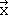 ) + (0 x
) + (0 x 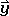 ) + (0 x
) + (0 x 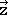 ) = -
) = - 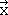 for the first character of the product matrix. Multiplying the second row of the matrix representation of C2 with the only column of the matrix for the old coordinates gives (0 x
for the first character of the product matrix. Multiplying the second row of the matrix representation of C2 with the only column of the matrix for the old coordinates gives (0 x 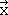 ) + (-1 x
) + (-1 x  ) + (0 x
) + (0 x 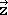 ) = -
) = -  for the second character of the product matrix. Multiplication of the third row of the matrix for C2 with the column of the matrix for the old coordinates gives (0 x
for the second character of the product matrix. Multiplication of the third row of the matrix for C2 with the column of the matrix for the old coordinates gives (0 x 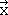 ) +(0 x
) +(0 x 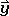 ) + (1 x
) + (1 x 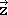 ) =
) =  This proves that the matrix correctly represents the symmetry operation C2.
This proves that the matrix correctly represents the symmetry operation C2.
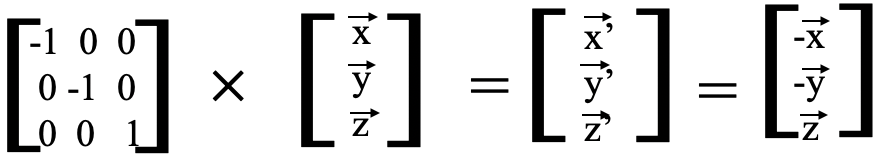
We can develop the matrix representation for the σ(xz) reflection operation along the same line we did for the C2 operation. Let us first think about how the vectors representing the coordinate changes as the reflection operation is carried out. The vectors  and
and  do not change because they are within the xz mirror plane. However, the
do not change because they are within the xz mirror plane. However, the 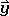 vector changes its direction as it is reflected to the other side of the mirror plane. Thus, the y-coordinate changes its algebraic sign.
vector changes its direction as it is reflected to the other side of the mirror plane. Thus, the y-coordinate changes its algebraic sign.

The matrix representing the new coordinates therefore has the form 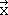 , -
, - 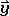 ,
, 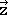 . The matrix that when multiplied with the matrix of the old coordinates, gives the matrix of the new coordinates must be the matrix representing the symmetry operation σxz. It has the form below (Fig. 2.3.10).
. The matrix that when multiplied with the matrix of the old coordinates, gives the matrix of the new coordinates must be the matrix representing the symmetry operation σxz. It has the form below (Fig. 2.3.10).
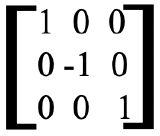
We could again show using the multiplication rules for matrices that multiplication of this matrix with the matrix for the old coordinates gives the matrix for the new coordinates (Fig. 2.3.11).
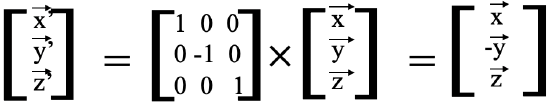
We can apply the same process for the σ(yz) symmetry operation. The σ(yz) mirror plane contains the coordinates y and z, and thus their vectors do not change upon the application of the symmetry operation. However, the vector  changes its direction upon reflection at the yz plane, and thus the algebraic sign of the x-coordinate changes (Fig. 2.3.12).
changes its direction upon reflection at the yz plane, and thus the algebraic sign of the x-coordinate changes (Fig. 2.3.12).
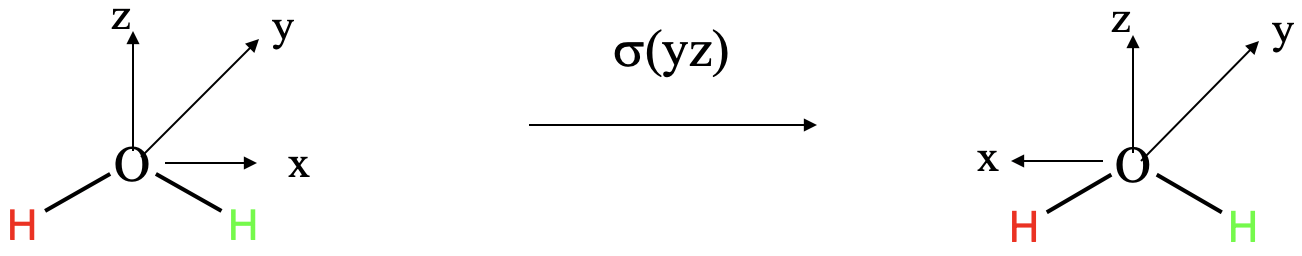
The matrix for the new coordinates is thus -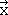 ,
, 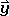 ,
, 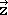 . In this case the matrix that when multiplied with the matrix of the old coordinates
. In this case the matrix that when multiplied with the matrix of the old coordinates  ,
, 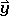 ,
, 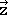 gives the matrix with the new coordinates -
gives the matrix with the new coordinates -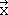 ,
, 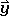 ,
, 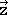 has the form below (Fig. 2.3.13).
has the form below (Fig. 2.3.13).
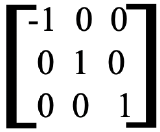
We could again use the multiplication rules for matrices to show that the above matrix is the correct matrix representation of the symmetry operation σ(yz), Fig. 2.3.14.
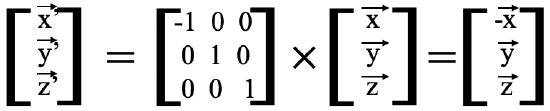

Lastly, we can also determine the matrix representation of the identity operation (Fig. 2.3.15). It has the form below (Fig. 2.3.16).
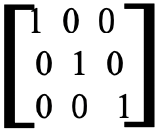
Like previously, we could use the multiplication rules to show that this matrix produces the correct matrix for the new coordinates. Since the identity does nothing to an object (Fig. 2.3.15), the new coordinates are the same as the old coordinates (Fig. 2.3.17).
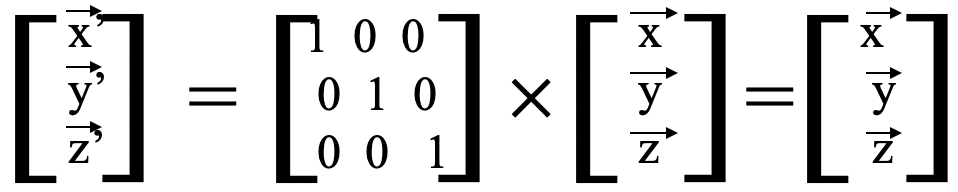
Reducible and Irreducible Representations
Let us look closer at the four matrices that we just derived (Fig. 2.3.18).
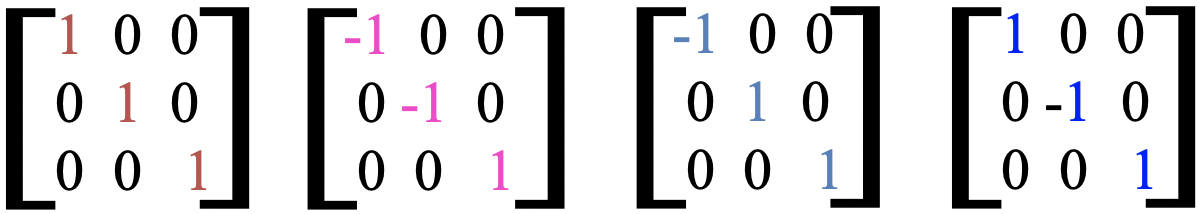
It is noteworthy that all characters are zero, except those on a diagonal that goes from the top left corner in the matrix to the bottom right corner. This diagonal is called the trace of the matrix. With good justification we can say that the characters on the trace of the matrix tell us what the symmetry operation does with a coordinate. If it is a -1 the algebraic sign of the coordinate changes, if it is +1, it does not. If we write the characters of the trace of the matrices that belong to a specific coordinate on a line underneath the symmetry operations, we get what is called an irreducible representation for the specific coordinate (Fig. 2.3.19).
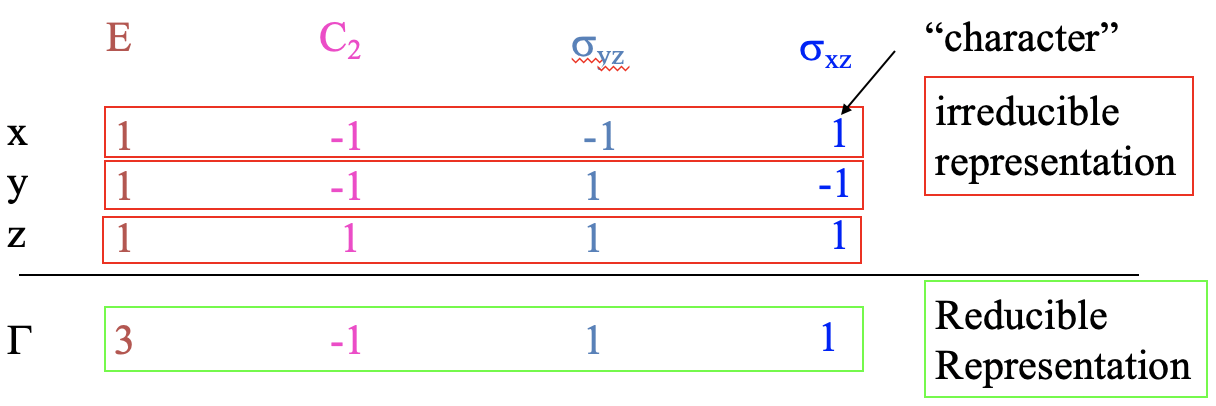
For example, for the x-coordinate the characters of the traces of the matrices for the symmetry operations E, C2, σyz, σxz, are 1, -1, -1, and 1, respectively. For the y-coordinate the characters would be 1, -1, 1, and -1, and for the z- coordinate they are 1, 1, 1, and 1. The use of an irreducible representation is that it tells us directly in a concise form what the symmetry operations do to a specific coordinate. The sum of two or more irreducible representations is a so-called reducible representation. If we sum up the three irreducible representations of Fig. 2.3.19, then this gives a reducible representation with the characters 1+1+1=3, (-1)+(-1)+1=-1, (-1)+1+1=1, and 1+(-1)+1=1. We will see about the use of reducible representations in a little bit.
Symmetry Types of Irreducible Representations
The specific characters in an irreducible representation determine the symmetry type of the irreducible representation. It is denoted by a capital letter with subscripts and/or superscripts. For example the irreducible representation for the x-coordinate is of the type B1 (Fig. 2.3.20)
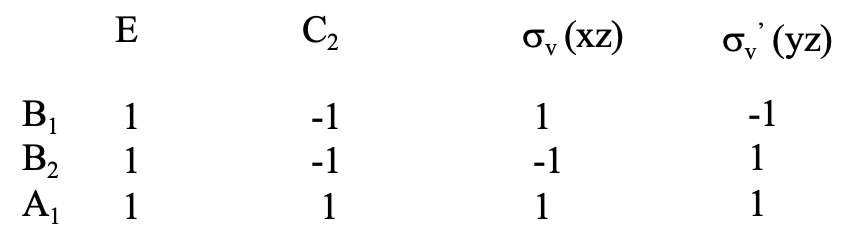
B means that the symmetry is anti-symmetric with regard to the principal axis (Fig. 2.3.21).

Anti-symmetric means that the algebraic sign of the coordinate changes as we rotate. In this case the principal axis is the C2 axis. We can see that the algebraic sign changes because the character of the irreducible representation for the x-coordinate underneath C2 is -1. The subscript 1 means that the representation is symmetric to a C2 perpendicular to the principal axis, or if lacking to a vertical σv (Figure 2.3.22)

In this case, we do not have a C2 perpendicular to the C2 which is our principal axis, but we have two vertical mirror planes. Symmetric means that the coordinate does not change its algebraic sign as the symmetry operation is carried out. We can see that this is true for the reflection with the lower number of primes which comes first in our considerations. It is indicated by the character +1 underneath the symmetry operation.
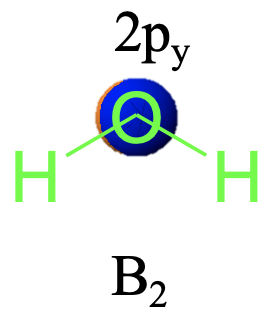
The irreducible representation of the y-coordinate has the symmetry type B2 (Fig.2.3.20) The symmetry type is again B, because the character underneath C2 is -1. The subscript is 2 in this case, and this means that the representation is antisymmetric to a C2 perpendicular to the principal axis or, if lacking to a vertical plane σv (Fig. 2.3.23)

We can see that the σv(xz) is anti-symmetric as indicated by the character -1 in the irreducible representation. Lastly, let us look at the symmetry type of the irreducible representation for the z-coordinate which is A1 (Fig. 2.3.20) A means symmetric with regard to rotation around the principle axis (Fig. 2.3.24).

We can confirm the symmetric situation for the rotation around z by verifying that the character underneath the principal axis C2 is +1.
Symmetry Types of Orbitals
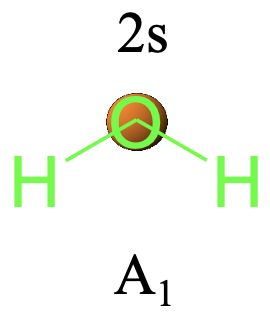
Irreducible representations are more powerful than only telling you the symmetry type of a specific coordinate in a point group. More generally, they can tell the symmetry type of a mathematical function in a specific point group. Remember, that orbitals are mathematically wave functions. Thus, it should be possible to assign orbitals to a symmetry type within a given point group. Let us look for example, at the 2s and the 2p orbitals of the oxygen atom in the water molecule. Let us consider the 2s orbital first, and determine what the symmetry operations do with it. We can see that no symmetry operation changes the 2s orbital in any way, thus all characters of the irreducible representation that belongs to the orbital should be +1. We can see that this is only the case for the irreducible representation with the symmetry type A1. Therefore we can say that the 2s orbital of the O-atom in the water molecule has the symmetry type A1 (Fig. 2.3.25).
Next, let us determine the symmetry type of the 2pz orbital. The 2pz orbital is oriented along the z-axis around which we rotate. When carrying a C2 operation we can see that this operation does not make any changes to the orbital. The same is true for the two reflection operations. Again, we can see that the symmetry operations do not change the 2pz orbital in any way, and therefore it also must belong to the symmetry type A1 (Fig. 2.3.26)
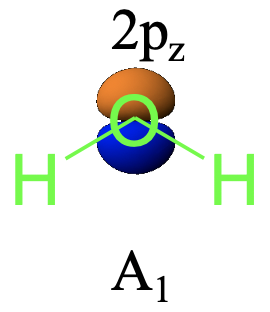
For the 2px orbital the situation is different though (Fig. 2.3.27). We can see that rotating around the C2 axis changes the algebraic sign of the orbital. This means that the 2px orbital should belong to a symmetry type which has a character of -1 for the C2 operation. We can see that this can be the B1 or the B2 symmetry type, but not A1. This rules out the A1 symmetry type. We still need to decide if the symmetry type is B1 or B2. For B1 reflection at the σv(xz) mirror plane would need to be symmetric, and for B2 it would need to be anti-symmetric. We can see that the orbital does not change when we carry out the σv (xz) reflection, and thus the symmetry type must be B1.

Lastly let us determine the symmetry type of the 2py orbital (Fig. 2.3.28). The 2py orbital is oriented perpendicular to the paper plane, the blue lobe points to the front, and the orange one, hardly visible points to the back. We can see that when we rotate around 180° the orange lobe points to the front, and the blue one points to the back. That means that the wave function of the orbital has changed its algebraic sign. Therefore, it must be of B symmetry type. Which one is it? B1 or B2? We can see that in this case the σv(xz) does change the algebraic sign of the wave function because the front lobe of the orbital gets reflected to the back, and the lobe in the back gets reflected to the front. Thus, it is antisymmetric with respect to σv(xz) and thus it must belong to the symmetry type B2.
We could have determined the symmetry types of the orbitals also from a more mathematical perspective. Remember when we discussed the atomic orbitals we saw that the wave function of a pz orbital is a linear function of the z-coordinate (Fig. 2.3.29). Therefore it has the same symmetry type as the z coordinate, namely A1. A py orbital is a linear function of y, therefore it has the same symmetry type as the coordinate y: B2. A px orbital is only a function of x, therefore its symmetry type is that of the coordinate x: B1. The 2s orbital is not a function of any coordinate. Because of that it must belong to the symmetry type in which all characters are +1 which is the A1 symmetry type in the point group C2v.
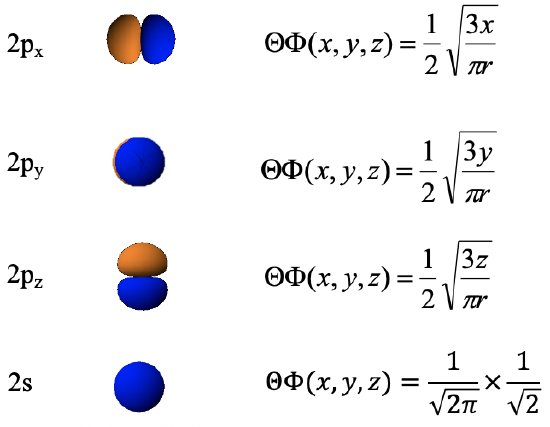
By the same means we can also determine the symmetry type of the d orbitals of the O atom in H2O. They are not occupied, and not involved in the bonding, but nonetheless they are possible states for the electrons. Let us determine them using the table below (Fig. 2.3.30)
Does the 3dz2 – orbital change when the symmetry operations are carried out (Fig. 2.3.31)? No, it does not! Therefore, it has the symmetry type A1.

What about the 3dxz? The 3dxz orbital changes its algebraic sign when the C2 operation is carried out, but not when the reflections are carried out. Therefore, it is of B1 symmetry type (Fig. 2.3.32).
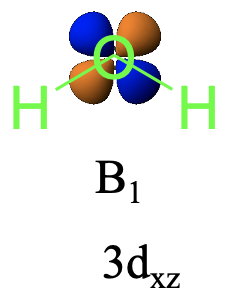
The 3dx2-y2-orbital also does not change when the symmetry operations are executed, thus it is of symmetry type A1 (Fig. 2.3.33)

For the dyz orbital rotation and the σv(xz) reflection changes the algebraic sign, therefore it is B2 (Fig. 2.3.24).

For the 3dxy we can see that rotation does not change the orbital, but the σv(xz) reflection does. This means that the symmetry type must be A2 (Fig. 2.3.35).

This is a new symmetry type which also belongs to the point group C2v. No single coordinate is of this symmetry type, but mathematical functions that are the product of the coordinates x and y, such as the 3dxy orbital are. Similarly, because the 3dz2 orbital is a function of z2 and the 3dz2 has the symmetry type A1 any function of z2 has this symmetry type. Analogously, any function which is the product of the x and the z coordinate belongs to the symmetry type B1, any function which is a function of x2-y2 belongs to the symmetry type A1, and any function which is a product of y and z belongs to the symmetry type B2.
Character Tables
There is only a finite number of irreducible representations and symmetry types in a specific point group.
Generally, all the irreducible representations that are possible in a specific point group define the so-called character table of the point group Fig. 2.3.36).
Definition: Character Table
A complete set of irreducible representations in a point group defines its character table
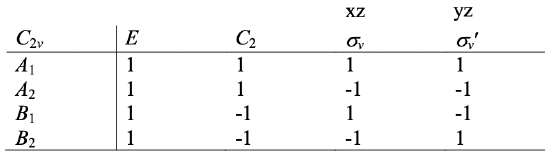
Character tables describe what the symmetry operations of a point group do with a mathematical function. You can see the complete character table of the point group C2v below (Fig. 2.3.36).
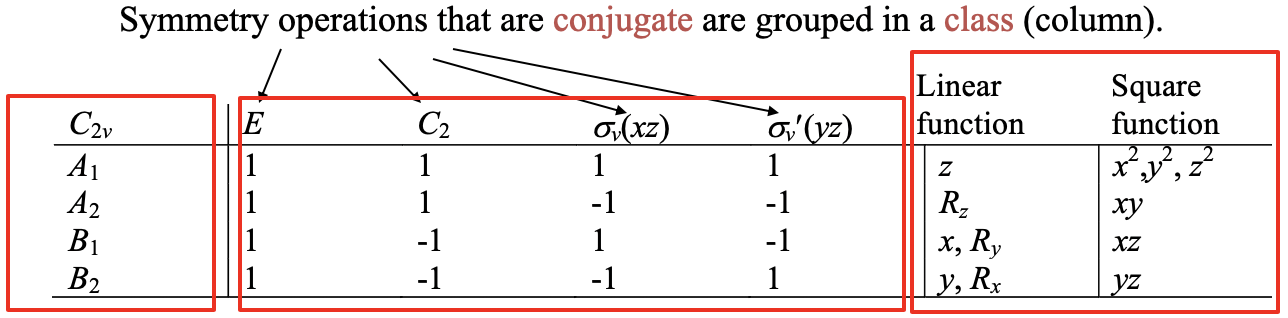
It is made of several rows and columns. In the first column you can find the point group symbol to the very left, and then the symbols for the different symmetry types of the irreducible representations the point group has. Then, there are several columns with symmetry operations in the first row, and the characters for the irreducible representations below. Each of these columns is called a class. Symmetry operations that are conjugate are grouped into the same column, or the same class. For the point group C2v, each operation gets its own column and that means that they are all non-conjugate. But this is not always true, in many other point groups there are several symmetry operations that are conjugate, and listed in the same column. We have already discussed qualitatively that conjugate operations transform the coordinates of an object in a similar way. Now we have a more exact definition which is that whenever the characters for the operations in their irreducible representations are the same, they belong to the same class.

The sum of characters underneath the identity operation E defines the dimension of the point group. For C2v the dimension of the point group is 1+1+1+1=4. The order (h) of the point group is just the sum of all symmetry operations in the point group. For C2v the order is 4. In the two far right columns of the character table you can find the mathematical functions that belong to the different irreducible representations. In the second column from the right linear and rotational functions are listed, and in the far right column square functions are listed. For example, the letter z is in the row associated with the symmetry type A1. This means that any linear function of the z-coordinate has the symmetry type A1. The letters x and y are in rows for the symmetry type B1 and B2 respectively. This means that any linear function of x and y has the symmetry type B1 and B2 respectively.
You can also see the symbols Rz, Rx, and Ry in the same column. These symbols stand for rotational functions around the z, x, and y axis respectively. Rz is in the row of the symmetry type A2, which means that any rotational function of z has the symmetry type A2. How can we understand that? Consider a rotational vector around z that indicates clockwise rotation (Fig. 2.3.37). If we rotate this vector by 180° counter-clockwise it will not change its direction, it will still point clock-wise, and thus the character underneath C2 in the character table should be a 1. This rules out that the symmetry is B type, it must be either A1 or A2 type. We can further see that when we reflect this vector at the two vertical mirror planes, it reverses its direction, now pointing counter-clockwise. Therefore, the characters underneath the two mirror planes should be both -1. This means that the symmetry type must be A2. If we did the same exercise with the Rx and the Ry rotational vectors we could show that they belong to the symmetry types B2 and B1 respectively. In the last column the square functions are listed. The row in which the function is located gives you the information about the symmetry type of the square function. For example any function of x2, y2, or z2 has the symmetry type A1, a function that is a product of x and y has the symmetry type A2 and so forth.
Matrix Representations of Symmetry Operations in C3v
Now let us go from the point group C2v to the point group C3v and determine the matrix representations of the symmetry operations. We will see that for this, and more generally for any point group with rotational axes with an order higher than 2, a symmetry degeneracy is possible, which means that two or even all three coordinates belong to the same symmetry type. The coordinates do not change independently upon the execution of a symmetry operation, they are linked to each other. Let us look at the ammonia molecule that belongs to the point group C3v.
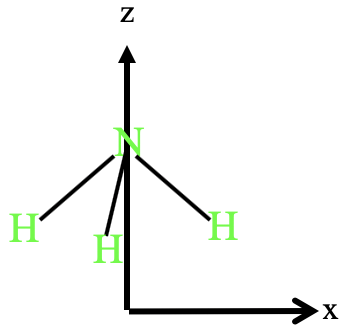
We can define the coordinate system so that the x-axis points to the right, the z-axis point to the to top , and the y-axis stands perpendicular to the paper plane (Fig. 2.3.38). The ammonia molecule is oriented so that its pyramid points into z-direction, and one of the three N-H bonds is within the xz plane.
Now let us see how the coordinates change when we rotate the molecule by an arbitrary general angle θ around the z-axis. In the diagram shown below, we now look along the z-axis, and the xy plane is within the paper plane (Fig. 2.3.39).
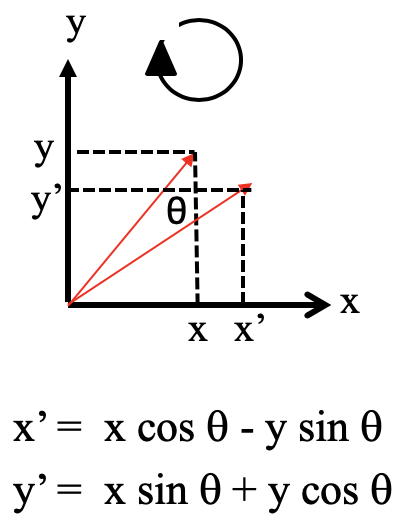
We can see that the rotation changes both the x and and the y coordinate together, but leaves the z-coordinate unaffected. According to trigonometry the new x-coordinate x’ is x’ = x cos θ - y sin θ. The new coordinate y’ is y’ = x sin θ + y cos θ.
The matrix representation of a symmetry operation that rotates around an arbitrary angle must be able to convert the old coordinates x,y,z into the new coordinates below (Fig. 2.3.40).
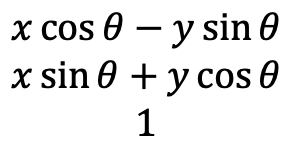
The matrix which is able to do this has the form below (Fig. 2.3.41)
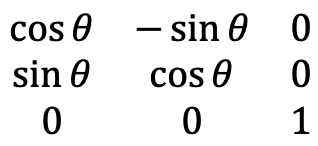
We could again use the multiplication rules for matrices to show that this matrix is the correct matrix.
The matrix that we just developed rotates around a general angle θ. What does this matrix look like in the point group C3v where we rotate around 120° and 240°? Well, all we need to do is to insert the values of 120° and 240° for θ into the matrix. The sinus of 120° is -√3/2, and the sinus of 240° is √3/2. The cosinus of 120° and 240° are both -1/2 (Fig. 2.3.42).
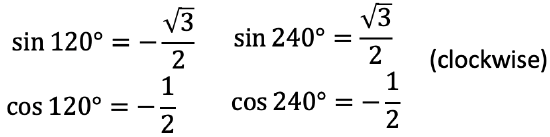
Note that these are the values for clockwise rotation. Because the C3 operations rotate anti-clockwise, we must use the values for the 240° rotation for the C31 and the values for the 120° rotation for the C32 operation. Considering this, the matrix for the C32 operation and the matrix for the C31 operation are the matrices shown below (Fig. 2.3.43).
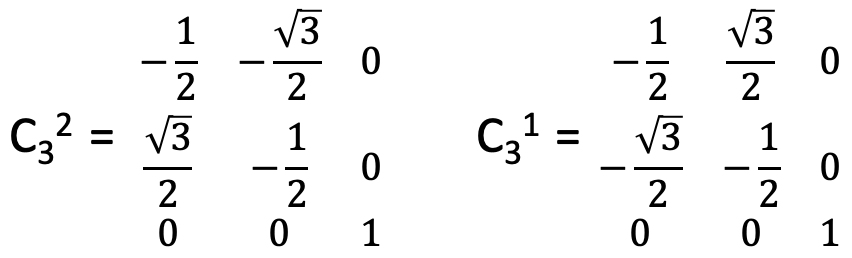
We can see there is a significant difference to the all the matrices we saw before. There are non-zero characters not only on the trace of the matrix, but also on other positions within the matrix, in particular in the first two rows which represent the x and the y coordinates. This is a consequence of the fact that the x and the y coordinates are no longer independent in C3v, they change in a dependent way. We say that they are degenerate.
Now can we determine the remaining symmetry operations in C3v. There are three conjugate vertical mirror planes to consider. The first mirror plane stands within the xz plane and passes through the N-H bond that is within the xz plane. The matrix for it is simple. It has the form below (Fig. 2.3.44).
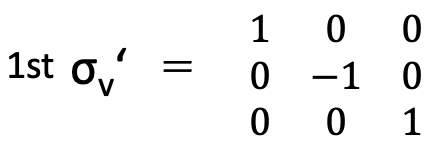
It is straightforward to understand why the matrix has this form. Because the mirror plane is in the xz plane the coordinates x and z are not affected by the reflection at this plane. Therefore there are two +1 characters on the trace of the matrix in the rows for the x and the z coordinates, respectively, and all other characters in these rows are 0. The character in the second row on the trace of the matrix is -1 because the algebraic sign of the y-coordinate changes as we reflect at the xz plane. However, the other two mirror planes are not co-planar with any two coordinates, and for these planes the x and the y coordinates are dependent again. The matrix for the second mirror plane and the matrix for the third one are shown below (Fig. 2.3.45).
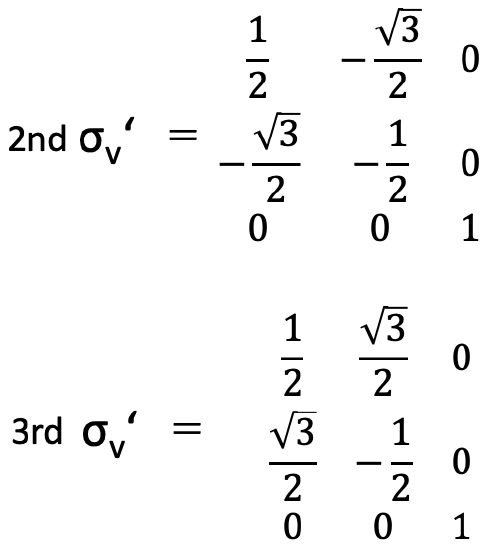
We will not derive them in detail here. It is enough for us to understand here that these matrices have more complex forms with non-zero values outside the trace of the matrix because of the degeneracy of the x and y coordinates. Lastly, we should not forget the identity. Because the identity does nothing with an object, its matrix is always the matrix below in any point group (Fig. 2.3.46).
Because we know now the matrix representations of the symmetry operations we can understand the character table for the point group C3v (Fig. 2.3.47)

The character table has three classes for the three groups of non-conjugate symmetry operations. In the first class there is only the identity. You can see that the second class contains the C31 and the C32 operations, summarized as 2C3. The third class contains the 3 conjugate σv operations. In the point group C3v there are three irreducible representations. The first two have the symmetry types A1 and A2 respectively, the third of is of type E. The last one is new to us. It stands for “double degeneracy”, and this symmetry type exists due to the double-degeneracy of the x and the y coordinate. You can see that the character table explicitly states that x and y are double-degenerate when you look into the last column of the character table. The letters x and y are in parentheses separated by a comma. The parentheses indicate the degeneracy of these two coordinates. More generally, any two functions that are linear functions of x or y are degenerate in C3v. You can see that there are also other functions that are degenerate. For instance functions of x2-y2 and xy are degenerate. Also functions of xz and yz are degenerate.
You can see that the characters in the irreproducible representation of the E symmetry type are also unusual. Previously, we only encountered the characters 1 and -1. However, the character underneath the identity is 2, and the character in the class for the vertical mirror planes is 0. How can we understand these characters? The answer has to do with the double-degeneracy of the x and y coordinates. Because of this double-degeneracy, the characters in the irreducible representations are the sum of the characters on the trace of the matrices for the x and y coordinate. Let us check what they are. You can see the three matrices representing the three classes of the symmetry operations below (Fig. 2.3.48).

For the identity the sum of the two characters is 1+1=2 which explains the character 2 in the irreducible representation E. For the matrix representing the C3 operations the characters on the trace of the matrix for x and y are -1/2. When summed up -1/2 + (-1/2) gives -1 which explains the character -1 in the irreducible representation. Lastly for the matrix representing the vertical mirror planes the characters on the trace of the matrix for the x and y coordinates are 1 and -1, respectively. -1+1=0 which explains the character 0 in the irreducible representation of the symmetry type E.
The z coordinate has the symmetry type A1 which is straightforward to understand because the characters for z on the trace of the matrices for the three different classes of symmetry operations are all 1. You can also see from the character table that there is again an irreducible representation to which no coordinate belongs to. It is the one with the symmetry type A2. In C3v only rotational functions around z have that symmetry type.
Symmetry Types of Degenerate Irreducible Representations
There are not only double-degenerate irreducible representations, denoted by a symbol E, there can also be triply-degenerate ones, indicated by a symbol T. In this case all three coordinates x, y, and z are degenerate. Triple-degeneracy does not appear in the point group C3v, but in other point groups, in particular the high-symmetry point groups (Fig. 2.3.49).

Both the E and T symbols can carry subscripts and primes that have specific meanings. The prime (‘) and (“) double prime in the symmetry representation label indicates “symmetric” or “anti-symmetric” with respect to σh, e.g. E` or E``(Fig. 2.3.50).
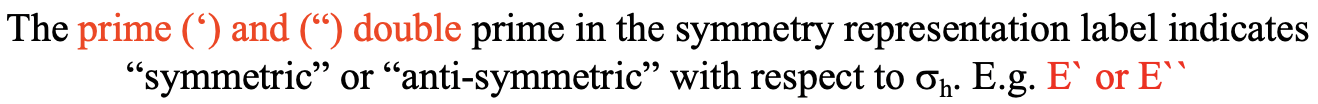
The subscripts g and u stand for the German words “gerade” and “ungerade” and a g and a u indicates “symmetric” or “anti-symmetric” with respect to inversion, i, respectively (Fig. 2.3.51).

For example, there can be symmetry types like Tg or Eu. There are other subscripts possible, and we do not need to go through them exhaustively. It is enough to understand that they indicate a certain symmetry property in a symmetry type.
Character Tables and Degenerated Orbitals
One of the most useful properties of character tables are that one can identify degenerate orbitals very easily. For example, a quick look into the character table of the point group C3v reveals that the 2px and the 2py orbital in NH3 must be degenerate (Fig. 2.3.52).
This is because the 2px orbital is a linear function of x, and the 2py orbital is a linear function of y, and linear functions of x and y are listed in parentheses in the double-degenerate irreducible representation of the type E. This double-degeneracy could also be derived by inspecting the orbitals in the NH3 molecule, but this is not as easy as looking up the character table. You can see the 2px and the 2py orbitals in the ammonia molecule below (Fig. 2.3.53).
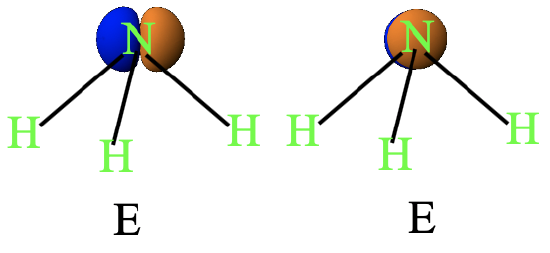
The two orbitals stand perpendicular to each other, but the NH3 molecule has C3 rotational symmetry. Therefore, why would the two orbitals be symmetry-degenerate? If they are degenerate, then there must be at least one symmetry operation that can interconvert the two orbitals. From the above depiction it not obvious what symmetry operation this could be.
Identifying the Double Degeneracy of 2px and 2py in NH3
We can do a little trick to see that a reflection operation is the one that can interconvert the two orbitals. The trick is to rotate the coordinate system by 45°. You can see the ammonia molecule in the bird’s perspective below (Fig. 2.3.54).
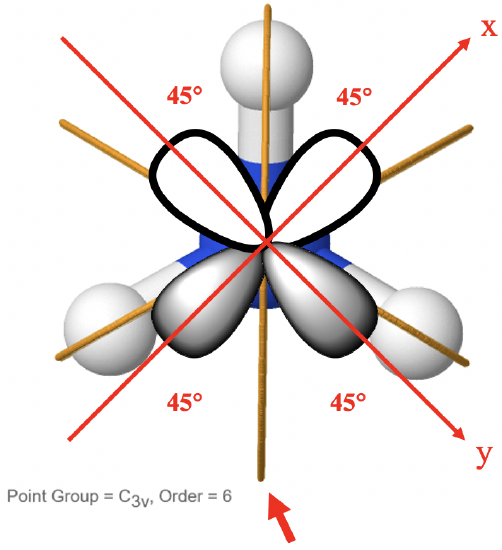
This means that we look perpendicular to the base of the pyramid. You can see the NH3 molecule with its three mirror planes above. Now we can choose our coordinate system so that the x and the y axes are rotated 45° with respect to one of the mirror planes. By definition, the 2px orbital must be oriented along the x-axis, and the 2py orbital must be oriented along the y-axis. You can see that one of the mirror planes, namely the one that oriented vertically, is able to interconvert the two orbitals. Upon reflection, the left and the right lobes of both orbitals will swap up their positions, so that after the symmetry operation is complete, the 2p orbitals are interconverted. Overall we can see that proving the degeneracy of two orbitals by inspection can be tricky. A quick look into the character table can tell us much more easily if two orbitals are degenerate.
Dr. Kai Landskron (Lehigh University). If you like this textbook, please consider to make a donation to support the author's research at Lehigh University: Click Here to Donate.


