2.1: Symmetry Elements and Operations
- Last updated
- Save as PDF
- Page ID
- 344573
Symmetry in Chemistry
Symmetry is actually a concept of mathematics and not of chemistry. However, symmetry, and the underlying mathematical theory for symmetry, group theory, are of tremendous importance in chemistry because they can be applied to many chemistry problems. For example it helps us to classify the structures of molecules and crystals, understand chemical bonding, predict vibrational spectra, and determine the optical activity of compounds. We will therefore first discuss the general foundations of symmetry and group theory, and then apply them to chemical problems, in particular chemical bonding.
Let us first find a definition for symmetry. Symmetry is very familiar to us as we associate symmetry with beauty, but very familiar things are not necessarily easy to define scientifically. One common definition is that symmetry is the self-similarity of an object. The more similar parts it has the more symmetric it appears. For example, we would argue that the two wings of the butterfly depicted look similar. If the left wing was very different from the right wing the butterfly would look less symmetric.

How can we measure the self-similarity, or symmetry of an object quantitatively? We can do this using the concept of the symmetry operation. It is defined as a movement of an object into an equivalent indistinguishable orientation. The number and kind of symmetry operations that can be carried out defines the symmetry of the object.
Definition: Symmetry Operation
Movement of an object into an equivalent indistinguishable orientation
Symmetry operations are carried out around so-called symmetry elements. A symmetry element is a point, line, or plane about which a symmetry operation is carried out. Let us understand know what symmetry elements and operations exist.
Definition: Symmetry Element
A point, line or plane about which a symmetry operation is carried out
The Identity Operation (E)
The most simple operation is the identity operation. It can be denoted by the Schoenflies symbol E. Schoenflies symbols are the most common symbols to denote a symmetry operation. The identity operation says that each object is self-similar to itself when you do not move it in any way. This is a trivial statement, but as we will see later, the identity operation is necessary to make the mathematical framework of symmetry, group theory, complete. The identity operation is present in any object. In the example of the depicted snail shell it is the only operation (Fig. 2.1.2).

The Proper Rotation Operation
The proper rotation operation is a counter-clockwise rotation about a proper rotational axis by an angle of 360° over an integer number n. After that rotation the object must be indistinguishable from its original form. That means that the object after the rotation must superimpose the original object before the rotation. For example, when n=4, then we rotate around 90°, and after that the object must superimpose its original form. The proper rotational axis is the symmetry element associated with the proper rotation operation. It’s Schoenflies symbol is Cn, whereby n is called the order of the rotational axis. A proper rotational operation has the symbol Cnm, whereby m counts the number of times the operation is carried out. Overall we rotate by and angle of 360°× m/n when we carry out an operation Cnm. This means that when m=n, then we have rotated around 360° (Fig. 2.1.3). Then all points in the object are at their original position. It is as though we had done nothing with the object. We can also say we have reached the identity E. In mathematical form we can say that Cnn=E. If we rotated one more time, Cn(n+1), then this would be equal to rotating only one time, and thus Cn(n+1)=Cn1. For example if n=4, then rotating four times around 90° will produce the identity. We have rotated around 4 x 90°=360° which is the same a though we had not rotated at all, because all points in the object are in their original position after a 360° rotation. If we rotated 5 times around 90°, it would the same as rotating only one time.
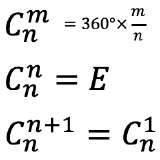
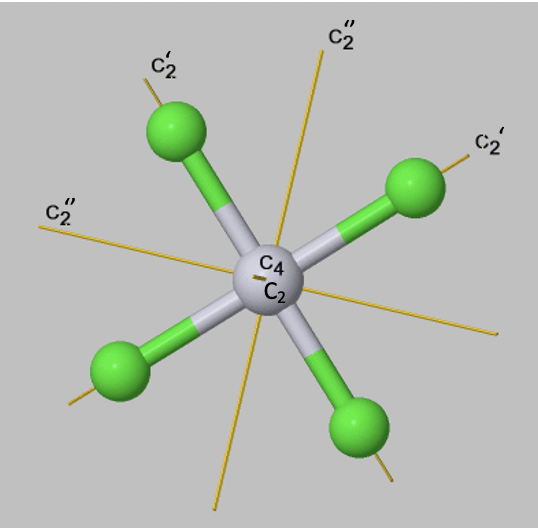
If an object has several axes with different order n, then the one with the highest order is called the principal axis. If there is more than one axis of the same order, then they get distinguished by primes if they are not conjugate. We will learn about the exact definition of conjugation somewhat later, we can however often see by inspection if two axes are conjugate. This is usually the case when they pass through the object in a equivalent way, and rotate the object in an equivalent way. Axes that pass through less many bonds, get less many primes. This is just a convention, but you have to follow it. An additional rule is that an axis which is in the same position as the principal axis gets the least number of primes. For example, a square planar molecule such as PtCl42- has a C4 principal axis standing perpendicular to the square plane of the molecule. There is an additional C2 axis where the C4 axis runs. It is present because one can also rotate around 180°, and not only around 90°. This C2 axis does not get any prime. You an see that there are four additional C2 axes, two of them are denoted C2’, and two others are denoted C2’’. You can see that the two axes which only have one prime pass through two Pt-Cl bonds, while the ones that have two primes, do not pass through any bonds. The two C2’ axes are conjugate, meaning that they transform the object in an equivalent way. The two C2’’ axes are also conjugate.
We can now think about how we can write out the axes and their associated proper rotational operations in a systematic way. Let us first look at the symmetry elements, the proper axes: We conventionally write the principal axis first, and then all other axes from their highest to their lowest order. When there are axes of the same order, those with the least number of primes get denoted first, and those with the highest number of primes last. If there are conjugate axes then their number is placed in front of their Schoenflies symbol. For the proper axes of the PtCl42- the notation would therefore be: C4, C2, 2C2', 2C2’’. Now let us see how to denote the rotation operations that are associated with these symmetry elements. The notation follows the same rules as for the symmetry elements. In addition, we have to consider that we must not count identical operations twice, we also do not denote the operations that are the same as the identity. For the C4 axis there are four operations until we reach the identity. C41, C42, C43, and C44. For each of the C2, C2’, and C2’’ elements there are two operations until the identity is reached. C21, C22, C21’, C22’, C21’’, C22’’. The C44, the C22, the C22’, and the C22’’are the same as the identity and therefore we do not consider them. In addition we can see that the C42 is the same as the C21. This is because the C4 and the C2 axes are in the same location, and rotating two times around 90° is the same as rotating one time around 180°. By convention we eliminate the operation associated with the higher order, thus the C42. The overall notation would then be: C41, C43, C21, 2 C21’ 2 C21’’ (Fig. 2.1.5).
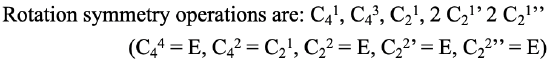
The Reflection Operations (σ)
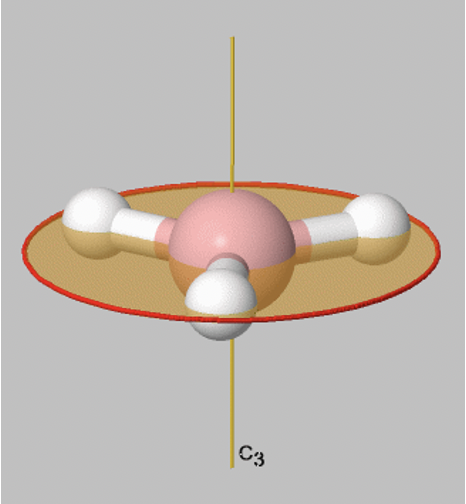
Let us look at reflection operations which are carried out around reflection planes, or mirror planes. Mirror planes have the Schoenflies symbol σ. When we carry out a reflection operation, then we move any point of the object to the other side of the mirror plane. There are two types of mirror planes, so-called horizontal mirror planes and vertical mirror planes. A horizontal mirror plane always stands perpendicular to the principal axis. For example in the depicted BH3 molecule there is a horizontal mirror plane that stands perpendicular to a C3 principal axis (Fig. 2.1.6). A horizontal mirror plane has the Schoenflies symbol σh.
A vertical mirror plane has the property that it contains the principal axis, this means that it is part of the principal axis. It is denoted σv. The BH3 molecule has three vertical axes that pass through the three B-H bonds. You can see that each of them contain the principal C3 axis (Fig. 2.1.7). The three vertical mirror planes are conjugate, and therefore they are not distinguished by primes. We can write a coefficient 3 in front of the symbol σv to indicate that there are three conjugate vertical mirror planes.
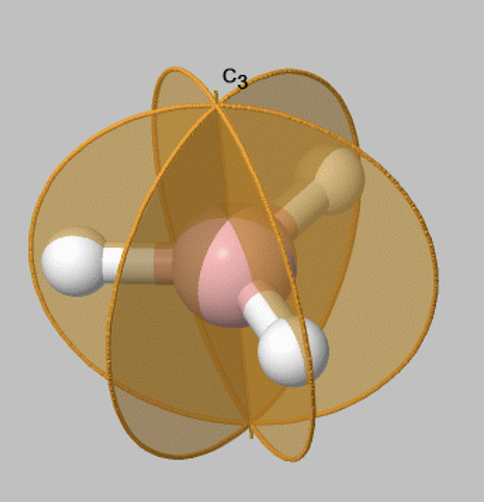
Now let us look at how many symmetry operations are associated with a particular mirror plane. Fortunately, things are simple here: There is only one reflection operation associated with one mirror plane. This because reflecting two times at a mirror plane produces the identity E: σv2=E. More generally, when we reflect n times, and n is an even number then this is the same as the identity or, σvn=E (n is even). When n is odd the reflecting n times is the same a reflecting only one time or, σvn=σv1 (n=odd).
The horizontal mirror plane of the BH3 molecule deserves an additional comment. Carrying out the horizontal reflection does not change the position of any atom. It is important to understand why the operation does exist despite the fact it does not change the position of any atom. The criterion is not whether the position of an atom is changed, but whether the position of the points in the object changes. In the case of the BH3 molecule the part of the molecule that is located above the mirror plane will be located below the mirror plane after the reflection operation has been carried out. Vice versa any part of the molecule that was formerly below the mirror plane will be located above the mirror plane after the reflection operation has been carried out. For example the lower half of the B atom with be above the mirror plane, and the half above the plane will be below the plane after the execution of the reflection operation.
Like non-conjugate proper rotations are distinguished by primes, also non-conjugate vertical mirror planes must be distinguished by primes. The smaller the number of bonds the vertical mirror plane contains, the larger the number of primes.
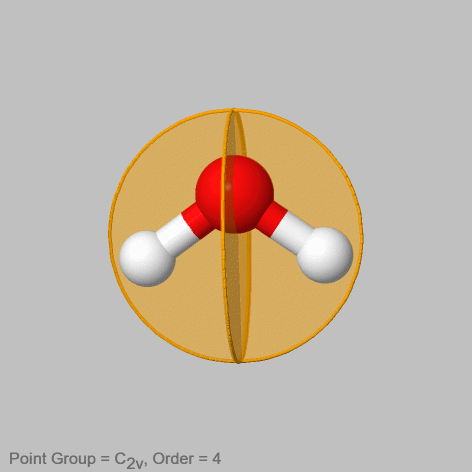
For example in the water molecule (Fig. 2.1.8) there are two non-conjugate vertical mirror planes. One contains the two O-H bonds, the other stands perpendicular to the first mirror plane. It is easy to see that these two mirror planes will not move the points in the atom in an equivalent way, and therefore they are not conjugate. The first mirror plane does not change the position of any atom, while the second one swaps the positions of the two hydrogen atoms. Therefore, the second mirror plane not containing any O-H bonds gets one prime the one that contains the O-H bonds doe not get a prime.
Dihedral Reflection Planes (σd)
A special case of a vertical mirror plane is a dihedral mirror plane, denoted σd. A dihedral mirror plane bisects the angle between two conjugate C2 axes.
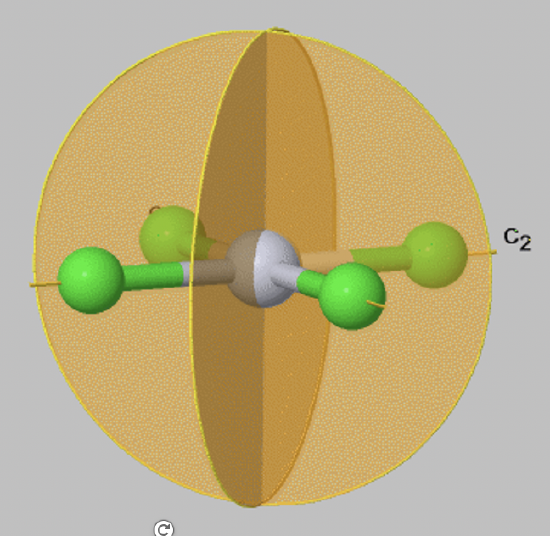
For example, in the PtCl42- anion (FIg. 2.1.9) there are two vertical mirror planes that bisect the angle between the two conjugate C2 axes that pass through the Pt-Cl bonds. Therefore, these mirror planes are vertical mirror planes σd.
The Inversion Operation (i)
Let us look next at the inversion operation which is symbolized by a Schoenflies symbol i. The symmetry element associated with an inversion, is the inversion center, also called center of symmetry. It is a single point. When an inversion operation is performed, then each point of the object is moved through the inversion center to the other side. Each coordinate in the object (x,y,z) is inverted into the coordinates (-x,-y,-z).
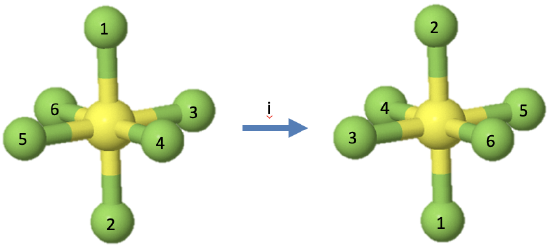
For example, the octahedral molecule SF6 has an inversion center in the center of the molecule (Fig. 2.1.10). When the inversion operation is carried out, then each fluorine atom is moved through the inversion center to the other side. This means that the fluorine atoms 1 and 2 swap up their positions, the fluorine atoms 3 and 5 swap up their positions, and so do the fluorine atoms 4 and 6. The sulfur atom does not change its position. There is only one inversion operation associated with each inversion center. Inverting two times, or more generally, an integer number of two times produces the identity. Inverting an odd number of times is the same as inverting one time.
The Rotation-Reflection Operation (Sn)
The rotation-reflection operation Sn is the most complex symmetry operation. It is carried out in two steps. First, a rotation around an improper axis is carried out. The angle is determined by the order n of the improper axis, and is 360°/n. This axis is called improper, because the object does not need to superimpose the original object after the rotation. Achieving superposition requires the second step which is the reflection at a mirror plane that stands perpendicular to the improper axis. Only after the second step the operation is complete. The presence of the rotation-reflection does not require a proper rotational axis or a regular mirror plane σ to exist, however it also do not preclude their existence.
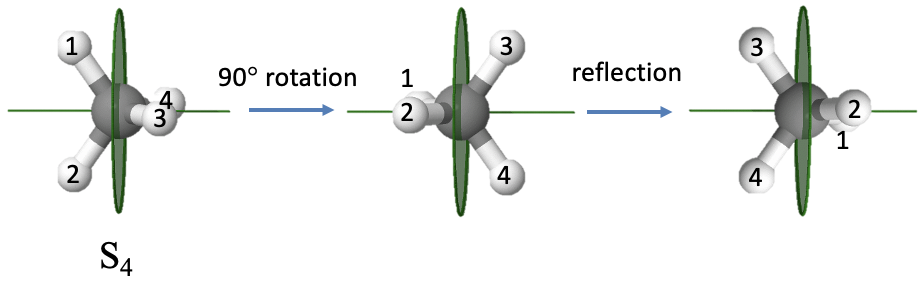
An example of a molecule with an improper axis is the methane molecule (Fig. 2.1.11). It has an S4 improper axis. The axis bisects the H-C-H tetrahedral bond angle. The order of the axis is four which requires that we rotate by 90° around this axis. You can see that after we carry out the rotation, the molecule does not superimpose the original molecule. Only after we reflect the rotated molecule at a mirror plane standing perpendicular to the improper axis the molecule superimposes the original molecule.
Properties of the Rotation-Reflection Operation (Sn)
The rotation-reflection has a number of interesting properties. One of the them is that an S1 operation is the same as a reflection. This is because the order 1 implies a rotation around 360° which produces the identity, and all points within the object are in their original position. This is the same as though we had not rotated at all. This means actually we only did the second step, the reflection, and therefore the S1 is identical to a “regular” reflection. The second property is that an S2 operation is the same as an inversion. When you rotate around 180° and then reflect perpendicular to the improper axis of rotation, the positions of the points in the object change exactly the same way as they do when you invert through an inversion center.

Look for example at the SF6 molecule again (Fig. 2.1.12) which has an inversion center in the center of the atom. We previously saw that when we carry out the inversion, the atoms 1 and 2 swap their position, and so do the atoms 3 and 5, as well as the atoms 4 and 6. Let us carry out the rotation-reflection, and see if the atoms change the same way. Firstly we rotate 180° around an axis that goes through the atoms 1 and 2. This leaves the positions of the atoms 1 and 2 unchanged, but swaps up the positions of the atoms 3 and 5, as well as the atoms 4 and 6. Next we must do a reflection at a plane that stands perpendicular to the improper axis. It is the plane defined by the atoms 3, 4, 5, and 6. Reflection at this plane does not change the positions of the atoms 3, 4, 5, and 6, but it swaps up the positions of the atoms 1 and 2, which lie above and below the plane, respectively. We can see that the positions of the atoms are the same as after the inversion.
The fact that we can express a reflection by an S1 rotation-reflection, and an inversion by a S2 rotation-reflection means that the reflection and the inversion are not independent symmetry operations, and we would not need them. The symmetry of an object could be fully described by the identity, proper rotations, and rotation-reflections. However, by convention, we use reflections and inversions instead of S1 and S2, simply because it is easier for the human mind to perform 1-step operations, rather than 2-step operations.
Improper rotations have different properties depending on whether the order of the axis is even or odd. For even orders, the presence of an Sn improper rotational axis implies that there must also be a proper rotational axis with an order n/2. For improper axes of even orders n the identity is produced after n rotation-reflections (Fig. 2.1.13).
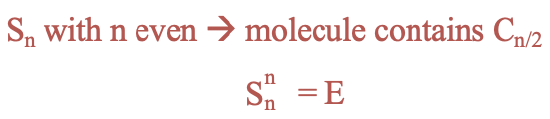
For improper axes of odd order n, carrying out the rotation-reflection n times is the same as carrying out a reflection at a horizontal mirror plane. We need to do the rotation-reflection 2n times to reach the identity (Fig. 2.1.4).
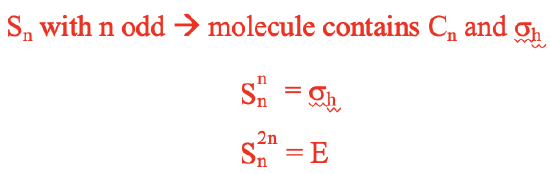
Rotation-Reflections of PF5 (an example with odd order)
Let us show these properties using two examples. Let us first look at an example with an improper rotation of odd order. The PF5 molecule has trigonal pyramidal shape with three F atoms in the equatorial plane, and two additional F atoms above and below the plane. The F atoms have been numbered from 1 to 5 as indicated by the subscripts that follow the element symbol (Fig. 2.1.15). The PF5 has an improper rotational axis S3 that stands perpendicular to the equatorial plane going through the P-F1 and P-F2 bonds. Let us carry out the S3 symmetry operations step by step and see how the atoms move.
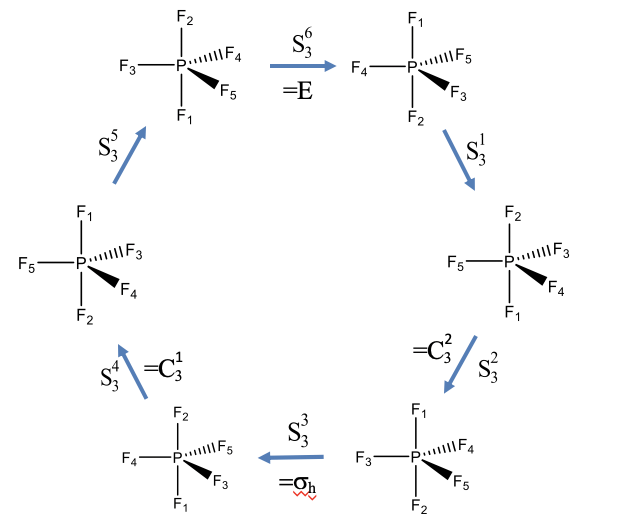
We would expect that after we carry out the operation six times the identity will be produced. After three rotation-reflections we would expect that the object has been moved the same way a horizontal mirror plane would do. After the first rotation-reflection the atoms F1 and F2 have swapped their positions, and the three F atoms in the equatorial plane have been rotated by 120 degrees counter-clockwise. The F5 atom now occupies the position of the F4, the F4 has been rotated into the position of the F3, and the F3 has been moved into the position of the F5. The second S3 operation again swaps up the F2 and F1 atoms, and rotates the remaining F atoms by 120°. Now the F5 atoms points toward us, the F4 atom points away from us, and the F3 atoms is in the paper plane. Carrying out the operation a third time again swaps the F1 and F2 and rotates F3, F4, and F5 counter-clockwise by 120°. Now let us compare the position of the atoms with the atom positions of the molecule we started with. We see that the position of the equatorial F atoms are same as in the beginning, but the position of the axial F1 and F2 atoms have been swapped up. This is equivalent to a reflection at a horizontal mirror plane located within the equatorial plane. This horizontal mirror plane would only swap up the axial F atoms, but would not move the equatorial ones. The S34 operation again swaps up the position of the F1 and the F2 atoms, and rotates the equatorial F atoms by 120° counter-clockwise. Now, F4 points toward us, F3 points away, and F5 is in the paper plane. After the fifth rotation-reflection F1 and F2 are again swapped so that F1 is below and F2 is above the equatorial plane. The atoms F3, F4 and F5 are rotated so that F3 is in the paper plane, F5 points toward us, and F4 points away from us. The sixth rotation-reflection again swaps up F1 and F2, and rotates the other F atoms around 120° counter-clockwise. We can now see that the produced molecule is the same as the one we started with, and the identity has been produced.
It is also noteworthy that the S32 and the S34 operation can be expressed by simpler operations, namely C32 and C31 proper rotation operations. We can understand this considering that an S32 operation requires that we reflect two times, and reflecting two times is just like not reflecting at all. So effectively, we only have two rotations around 120° which is equivalent to C32. Similarly, the S34 operation requires to reflect four times, which is the same as not reflecting at all. Thus, effectively, we only rotate four times around 120°. This is the same as rotating only one time around this angle, which is equivalent to a C31 operation.
Using similar considerations, we can also understand why the S33 operation is equivalent to a σh. In this case, we rotate 3 x 120° = 360°, and rotating around 360° is the same as not rotating at all. In addition, we carry out a reflection three times. Reflecting an odd number of times is the same as reflecting only one time. Thus overall, we effectively carry out a single reflection only.
Overall, only the S31 and the S35 operations are unique, all others can be expressed by other, simpler operations.
Rotation-Reflections of CH4 (an example with even order)
Let us illustrate the properties of an improper rotational axis with even order using the example methane (Fig. 2.1.16).
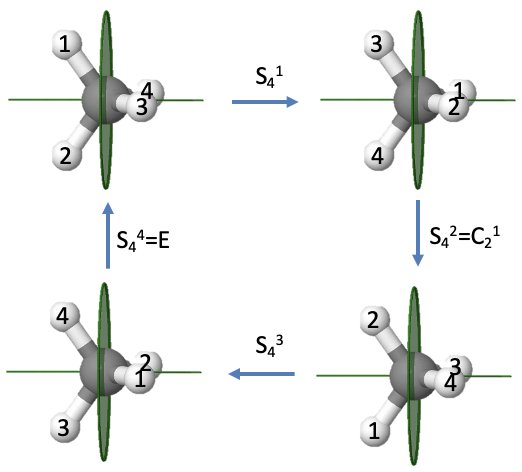
We previously saw that the methane molecule has an S4 improper axis. Executing the symmetry operation once moves the H atoms 1 and 2 to the right, whereby atom 1 points to the back and atom 2 points to the front. After the second rotation-reflection the atoms 1 and 2 are reflected back to the left side, but because we have rotated two times by 90° atom 2 points up, and atom 1 points down. Similarly, atoms 3 and 4 are reflected back to the right side, but atom four points toward us and atom 3 points to the back. After three rotation-reflections, the atoms 1 and 2 are again on the right side with atom 2 pointing to the back and atom 1 pointing to the front. Atoms 3 and 4 are on the left with atom 4 pointing up, and atom 3 pointing downward. After the operation is carried out four times, all atoms are back in their original position, meaning the identity has been produced. This is what we expected for an improper rotation of even order. We can see in addition that the S42 operation is the same as an C2 operation. Rotating two times about 90° is the same as rotating about 180°. Reflecting two times is the same as not reflecting at all. Therefore, effectively, we only rotated by 180° which is the same as what a C21 operation does. Because an S42 can be expressed by a C21, and an S44 is the same as the identity, only the S41 and the S43 are unique symmetry operations.
The Symmetry of a Molecule
We have now discussed all types of symmetry elements and operations that can exist in an object. Next, let us think about how we can define the overall symmetry of an object. The overall symmetry of an object is defined as the sum of all the symmetry operations for this object. If two objects have exactly the same symmetry elements and operations then their symmetry is the same. Using the mathematical language of group theory, the mathematical theory for symmetry, we can say they belong to the same point group. The name point group comes from the fact, that it has at least one invariant point. The number of symmetry operations belonging to a point group is called the order of the point group. Let us see next what different point groups we know and how we can systematically classify them.
Dr. Kai Landskron (Lehigh University). If you like this textbook, please consider to make a donation to support the author's research at Lehigh University: Click Here to Donate.


