5.2: Molecular Formulas and Empirical Formulas
- Page ID
- 227570
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Learning objective
- Determine the empirical and molecular formulas from combustion data
Empirical and Molecular formulas
Molecular formulas tell you how many atoms of each element are in a compound, and empirical formulas tell you the simplest or most reduced ratio of elements in a compound. If a compound's molecular formula cannot be reduced anymore, then the empirical formula is the same as the molecular formula. Combustion analysis can determine the empirical formula of a compound, but cannot determine the molecular formula (other techniques can though). Once known, the molecular formula can be calculated from the empirical formula.
Empirical Formulas
An empirical formula tells us the relative ratios of different atoms in a compound. The ratios hold true on the molar level as well. Thus, H2O is composed of two atoms of hydrogen and 1 atom of oxygen. Likewise, 1.0 mole of H2O is composed of 2.0 moles of hydrogen and 1.0 mole of oxygen. We can also work backwards from molar ratios since if we know the molar amounts of each element in a compound we can determine the empirical formula.
Example \(\PageIndex{1}\): Mercury Chloride
Mercury forms a compound with chlorine that is 73.9% mercury and 26.1% chlorine by mass. What is the empirical formula?
Let's say we had a 100 gram sample of this compound. The sample would therefore contain 73.9 grams of mercury and 26.1 grams of chlorine. How many moles of each atom do the individual masses represent?
For Mercury:
\[(73.9 \;g) \times \left(\dfrac{1\; mol}{200.59\; g}\right) = 0.368 \;moles\]
For Chlorine:
\[(26.1\; g) \times \left(\dfrac{1\; mol}{35.45\; g}\right) = 0.736\; mol \]
What is the molar ratio between the two elements?
\[\dfrac{0.736 \;mol \;Cl}{0.368\; mol\; Hg} = 2.0 \]
Thus, we have twice as many moles (i.e. atoms) of Cl as Hg. The empirical formula would thus be (remember to list cation first, anion last):
Combustion Analysis in a CHNS analyzer
One of the most common ways to determine the elemental composition of an unknown hydrocarbon is an analytical procedure called combustion analysis. A small, carefully weighed sample of an unknown compound that may contain carbon, hydrogen, nitrogen, and/or sulfur is burned in an oxygen atmosphere, and the quantities of the resulting gaseous products (CO2, H2O, N2, and SO2, respectively) are determined by one of several possible methods. This procedure is usually performed in a CHNS Analyzer (also known as a carbon-hydrogen, nitrogen, and sulfur analyzer, Figure \(\PageIndex{1}\)). These analyzers are capable of handling a wide variety of sample types, including solids, liquids, volatile and viscous samples.
The general procedure used in combustion analysis is outlined schematically in Figure \(\PageIndex{2}\) and a typical combustion analysis is illustrated in Examples \(\PageIndex{1}\). Since this methodology require that O2 must be added externally to burn the sample, the content of O in the organic compound cannot be measured directly. Therefore, it must be calculated by subtracting the mass of any other elements from the total mass of sample. Example 1 shows an example of how to calculate a empirical formula from a combustion analysis. Other elements, such as metals, can be determined by other methods.

Figure \(\PageIndex{1}\): Combustion analysis apparatus . Image by MaRufaru82, CC BY-SA 4.0, via Wikimedia Commons

Example \(\PageIndex{1}\): Combustion of Isopropyl Alcohol
What is the empirical formulate for isopropyl alcohol (which contains only C, H and O) if the combustion of a 0.255 grams isopropyl alcohol sample produces 0.561 grams of CO2 and 0.306 grams of H2O?
Solution
From this information quantitate the amount of C and H in the sample.
\[ (0.561\; \cancel{g\; CO_2}) \left( \dfrac{1 \;mol\; CO_2}{44.0\; \cancel{g\;CO_2}}\right)=0.0128\; mol \; CO_2 \]
Since one mole of CO2 is made up of one mole of C and two moles of O, if we have 0.0128 moles of CO2 in our sample, then we know we have 0.0128 moles of C in the sample. How many grams of C is this?
\[ (0.0128 \; \cancel{mol\; C}) \left( \dfrac{12.011\; g \; C}{1\; \cancel{mol\;C}}\right)=0.154\; g \; C \]
How about the hydrogen?
\[ (0.306 \; \cancel{g\; H_2O}) \left( \dfrac{1\; mol \; H_2O}{18.0\; \cancel{g \;H_2O}}\right)=0.017\; mol \; H_2O \]
Since one mole of H2O is made up of one mole of oxygen and two moles of hydrogen, if we have 0.017 moles of H2O, then we have 2*(0.017) = 0.034 moles of hydrogen. Since hydrogen is about 1 gram/mole, we must have 0.034 grams of hydrogen in our original sample.
When we add our carbon and hydrogen together we get:
0.154 grams (C) + 0.034 grams (H) = 0.188 grams
But we know we combusted 0.255 grams of isopropyl alcohol. The 'missing' mass must be from the oxygen atoms in the isopropyl alcohol:
0.255 grams - 0.188 grams = 0.067 grams oxygen
This much oxygen is how many moles?
\[ (0.067 \; \cancel{g\; O}) \left( \dfrac{1\; mol \; O}{15.994\; \cancel{g \;O}}\right)=0.0042\; mol \; O \]
Overall therefore, we have:
- 0.0128 moles Carbon
- 0.0340 moles Hydrogen
- 0.0042 moles Oxygen
Divide by the smallest molar amount to normalize:
- C = 3.05 atoms
- H = 8.1 atoms
- O = 1 atom
Within experimental error, the most likely empirical formula for propanol would be \(C_3H_8O\)
Molecular Formula from Empirical Formula
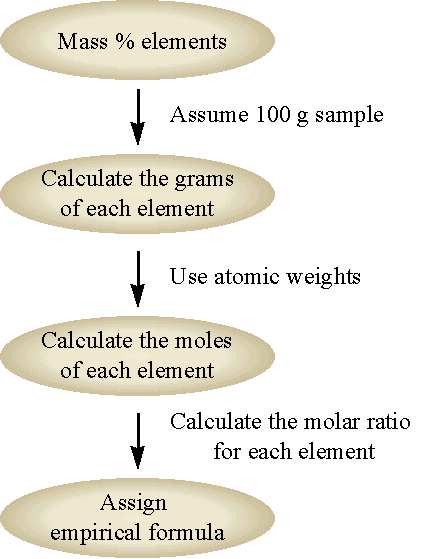
The chemical formula for a compound obtained by composition analysis is always the empirical formula. We can obtain the chemical formula from the empirical formula if we know the molecular weight of the compound. The chemical formula will always be some integer multiple of the empirical formula (i.e. integer multiples of the subscripts of the empirical formula). The general flow for this approach is shown in Figure \(\PageIndex{3}\) and demonstrated in Example \(\PageIndex{2}\).
Example \(\PageIndex{2}\): Ascorbic Acid
Vitamin C (ascorbic acid) contains 40.92 % C, 4.58 % H, and 54.50 % O, by mass. The experimentally determined molecular mass is 176 amu. What is the empirical and chemical formula for ascorbic acid?
Solution
Consider an arbitrary amount of 100 grams of ascorbic acid, so we would have:
- 40.92 grams C
- 4.58 grams H
- 54.50 grams O
This would give us how many moles of each element?
- Carbon
\[ (40.92\; \cancel{g\; C}) \times \left( \dfrac{1\; mol\; C}{12.011\; \cancel{g\; C}} \right) = 3.407\; mol \; C \]
- Hydrogen
\[ (4.58\; \cancel{g\; H}) \times \left( \dfrac{1\; mol\; H}{1.008\; \cancel{g\; H}} \right) = 4.544\; mol \;H \]
- Oxygen
\[ (54.50\; \cancel{g\; O}) \times \left( \dfrac{1\; mol\; O}{15.999\; \cancel{g\; O}} \right) = 3.406\; mol \; O \]
Determine the simplest whole number ratio by dividing by the smallest molar amount (3.406 moles in this case - see oxygen):
- Carbon
\[ C= \dfrac{3.407\; mol}{3.406\; mol} \approx 1.0\]
- Hydrogen
\[ C= \dfrac{4.5.44\; mol}{3.406\; mol} = 1.0\]
- Oxygen
\[ C= \dfrac{3.406\; mol}{3.406\; mol} = 1.0\]
The relative molar amounts of carbon and oxygen appear to be equal, but the relative molar amount of hydrogen is higher. Since we cannot have "fractional" atoms in a compound, we need to normalize the relative amount of hydrogen to be equal to an integer. 1.333 would appear to be 1 and 1/3, so if we multiply the relative amounts of each atom by '3', we should be able to get integer values for each atom.
C = (1.0)*3 = 3
H = (1.333)*3 = 4
O = (1.0)*3 = 3
or
C3H4O3
This is our empirical formula for ascorbic acid.
What about the chemical formula? We are told that the experimentally determined molecular mass is 176 amu. What is the molecular mass of our empirical formula?
(3*12.011) + (4*1.008) + (3*15.999) = 88.062 amu
The molecular mass from our empirical formula is significantly lower than the experimentally determined value. What is the ratio between the two values?
(176 amu/88.062 amu) = 2.0
Thus, it would appear that our empirical formula is essentially one half the mass of the actual molecular mass. If we multiplied our empirical formula by '2', then the molecular mass would be correct. Thus, the actual molecular formula is:
2* C3H4O3 = C6H8O6
Exercise 1
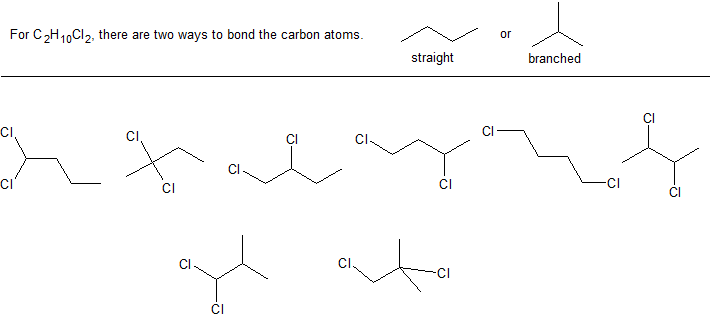
Elemental analysis of an organic compound indicates its composition to be 37.82% carbon, 6.36% hydrogen, and 55.82% chlorine.
a. What is the empirical formula for this compound?
b. Mass spectral analysis indicates a molar mass of 129 g/mol. What is the molecular formula for this compound?
c. Draw all the possible bond-line structures with this molecular formula.
Solutions to Exercise 1
a. C2H5Cl with a molar mass of 64.5 g/mol
b. C4H10Cl2
c. There 8 possible structures with the molecular formula C4H10Cl2. It can help to start with the different carbon backbones and then systematically add any branches (substituents).
Molecular Formula from Empirical Formula
The chemical formula for a compound obtained by composition analysis is always the empirical formula. We can obtain the chemical formula from the empirical formula if we know the molecular weight of the compound. The chemical formula will always be some integer multiple of the empirical formula (i.e. integer multiples of the subscripts of the empirical formula). The general flow for this approach is shown in Figure \(\PageIndex{1}\) and demonstrated in Example \(\PageIndex{2}\).

Contributors and Attributions
- Molecular Formulas and Empirical Formulas (Review). (2020, May 30). Retrieved May 24, 2021, from https://chem.libretexts.org/@go/page/44636
- Wikipedia contributors. (2021, April 15). CHN analyzer. In Wikipedia, The Free Encyclopedia. Retrieved 14:43, May 24, 2021, from https://en.wikipedia.org/w/index.php?title=CHN_analyzer&oldid=1018003336