9.10: Molecular Orbital Theory Predicts that Molecular Oxygen is Paramagnetic
- Page ID
- 204581
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)In general chemistry courses, students learn that covalent bonds can come as either single, double or triple bonds, which are identifies by their bond order. Both bond length and bond energy changes as the bond order increases and as the number of electrons shared between two atoms in a molecule increases, the bond order of a bond increases, the strength of the bond increases and the distance between nuclei decreases (Table \(\PageIndex{1}\)).
| Bond | Bond Order | Bond Enthalpy (kJ/mol) | Bond Length (Å) |
|---|---|---|---|
| \(\ce{C-C}\) | 1 | 348 | 1.54 |
| \(\ce{C=C}\) | 2 | 614 | 1.34 |
| \(\ce{C#C}\) | 3 | 839 | 1.20 |
| \(\ce{N-N}\) | 1 | 163 | 1.47 |
| \(\ce{N=N}\) | 2 | 418 | 1.24 |
| \(\ce{N#N}\) | 3 | 941 | 1.10 |
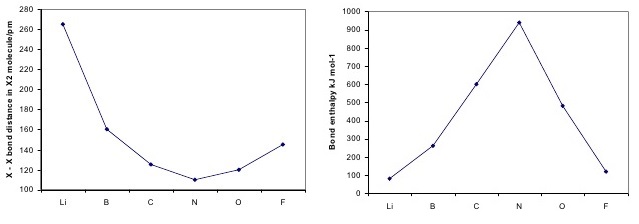
The above trend can be observed in the first row diatomics in Figure \(\PageIndex{1}\). The bond order can be determined directly form the molecular orbital electron configurations.
\[\text{bond order} = \dfrac{\text{number of electrons in bonding MOs}- \text{number of electrons in antbonding MOs}}{2} \label{BO}\]
For diatomics, the occupations can correlate to bond length, bond energies (Figure \(\PageIndex{1}\)) and behavior in applied magnetic fields.
Example \(\PageIndex{1}\): Molecular Oxygen
Arrange the following four molecular oxygen species in order of increasing bond length: \(\ce{O_2^+}\), \(\ce{O_2}\), \(\ce{O_2^-}\), and \(\ce{O_2^{2-}}\).
Solution
The bond length in the oxygen species can be explained by the positions of the electrons in molecular orbital theory. To obtain the molecular orbital energy-level diagram for \(\ce{O2}\), we need to place 12 valence electrons (6 from each O atom) in the energy-level diagram shown in Figure \(\PageIndex{1}\). We again fill the orbitals according to Hund’s rules and the Pauli principle, beginning with the orbital that is lowest in energy. Two electrons each are needed to fill the σ2s and σ2s* orbitals, two more to fill the \( \sigma _{2p_{z}} \) orbital, and 4 to fill the degenerate \( \pi _{2p_{x}}^{\star }\) and \( \pi _{2p_{y}}^{\star}\) orbitals. According to Hund’s first rule, the last 2 electrons must be placed in separate \(π^*\) orbitals with their spins parallel, giving a multiplicity of 3 (a triplet state) with two unpaired electrons. This leads to a predicted bond order of
\[\dfrac{8 − 4}{2} = 2 \nonumber\]
which corresponds to a double bond, in agreement with experimental data: the O–O bond length is 120.7 pm, and the bond energy is 498.4 kJ/mol at 298 K.
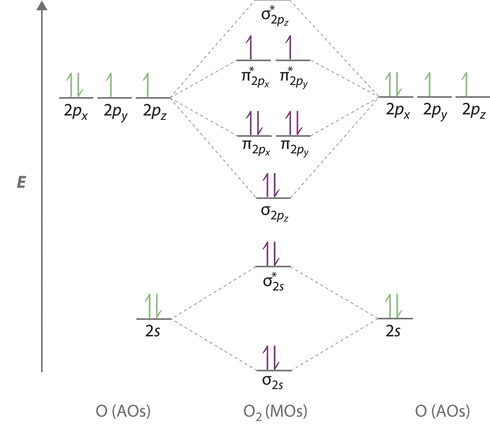
The bond order is determined from the the electron configurations via Equation \(\ref{BO}\). The electron configurations for the four species are contrasted below.
- \(\ce{O_2}\): \[σ_{1s}^2 {σ^*_{1s}}^2 σ_{2s}^2 {σ^*_{2s}}^2 σ_{2p}^2 π_{2p_y}^2 {π^*_{2p_y}}^2 π_{2p_x}^1 {π^*_{2p_y}}^1 \nonumber \] From Equation \ref{BO}, the bond order for \(O_2\) is 2 (i.e., a double bond).
- \(\ce{O_2^{+}}\): \[σ_{1s}^2 {σ^*_{1s}}^2 σ_{2s}^2 {σ^*_{2s}}^2 σ_{2p}^2 π_{2p_y}^2 {π^*_{2p_y}}^2 π_{2p_x}^1 {π^*_{2p_y}}^0 \nonumber \] From Equation \ref{BO}, the bond order for \(O_2^{+}\) is 2.5. An alternative and equally valid configuration is \[σ_{1s}^2 {σ^*_{1s}}^2 σ_{2s}^2 {σ^*_{2s}}^2 σ_{2p}^2 π_{2p_y}^2 {π^*_{2p_y}}^2 π_{2p_x}^0 {π^*_{2p_y}}^1 \nonumber \]
- \(\ce{O_2^{-}}\): \[σ_{1s}^2 {σ^*_{1s}}^2 σ_{2s}^2 {σ^*_{2s}}^2 σ_{2p}^2 π_{2p_y}^2 {π^*_{2p_y}}^2 π_{2p_x}^2 {π^*_{2p_y}}^1 \nonumber \] From Equation \ref{BO}, the bond order for \(O_2^{-}\) is 1.5. An alternative and equally valid configuration is \[σ_{1s}^2 {σ^*_{1s}}^2 σ_{2s}^2 {σ^*_{2s}}^2 σ_{2p}^2 π_{2p_y}^2 {π^*_{2p_y}}^2 π_{2p_x}^1 {π^*_{2p_y}}^2 \nonumber \]
- \(\ce{O_2^{2-}}\): \[σ_{1s}^2 {σ^*_{1s}}^2 σ_{2s}^2 {σ^*_{2s}}^2 σ_{2p}^2 π_{2p_y}^2 {π^*_{2p_y}}^2 π_{2p_x}^2 {π^*_{2p_y}}^2 \nonumber \] From Equation \ref{BO}, the bond order for \(O_2^{2-}\) is 1.
The bond order decreases and the bond length increases in the order. The predicted order of increasing bondlength then is \(\ce{O_2^+}\) < \(\ce{O_2}\) < \(\ce{O_2^-}\) < \(\ce{O_2^{2-}}\). This trend is confirmed experimentally with \(\ce{O_2^+}\) (112.2 pm), \(\ce{O_2}\) (121 pm), \(\ce{O_2^-}\) (128 pm) and \(\ce{O_2^{2-}}\) (149 pm).
Molecular Oxygen is Paramagnetic
We now turn to a molecular orbital description of the bonding in \(\ce{O2}\). It so happens that the molecular orbital description of this molecule provided an explanation for a long-standing puzzle that could not be explained using other bonding models. None of the other bonding models (e.g., Valence Bond theory or Lewis bonding) can predict the presence of two unpaired electrons in \(\ce{O_2}\). Chemists had long wondered why, unlike most other substances, liquid \(\ce{O_2}\) is attracted into a magnetic field. As shown in Figure \(\PageIndex{2}\), it actually remains suspended between the poles of a magnet until the liquid boils away. The only way to explain this behavior was for \(\ce{O_2}\) to have unpaired electrons, making it paramagnetic. This result was one of the earliest triumphs of molecular orbital theory over the other bonding approaches.
Advanced: Spin Barriers
The magnetic properties of O2 are not just a laboratory curiosity; they are absolutely crucial to the existence of life. Because Earth’s atmosphere contains 20% oxygen, all organic compounds, including those that compose our body tissues, should react rapidly with air to form H2O, CO2, and N2 in an exothermic reaction. Fortunately for us, however, this reaction is very, very slow. The reason for the unexpected stability of organic compounds in an oxygen atmosphere is that virtually all organic compounds, as well as H2O, CO2, and N2, have only paired electrons, whereas oxygen has two unpaired electrons. Thus the reaction of O2 with organic compounds to give H2O, CO2, and N2 would require that at least one of the electrons on O2 change its spin during the reaction. This would require a large input of energy, an obstacle that chemists call a spin barrier.

