17.5: Express the Pressure in Terms of a Partition Function
- Page ID
- 204052
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Pressure can also be derived from the canonical partition function. The average pressure is the sum of the probability times the pressure:
\[ \langle P \rangle = \sum_i{P_i(N,V,T)P_i(N,V)} \nonumber \]
The pressure of a macroscopic system is:
\[ P(N,V) = -\left(\dfrac{\partial E_i}{\partial V}\right)_N \nonumber \]
So we can write the average pressure as:
\[\begin{split} \langle P \rangle &= \sum_i{P_i(N,V,\beta)\left(-\dfrac{\partial E_i}{\partial V}\right)_N} \\ &= \sum_i{\left(-\dfrac{\partial E_i}{\partial V}\right)_N\dfrac{e^{-E_i(N,V)/kT}}{Q(N,V,T)}} \end{split} \nonumber \]
In a few steps we can show that the temperature can be expressed in terms of the partition function:
\[ Q(N,V,T) = \sum_i{e^{-E_i(N,V)/kT}} \nonumber \]
Writing in terms of \(\beta\) instead of temperature:
\[ Q(N,V,\beta) = \sum_i{e^{-\beta E_i(N,V)}} \nonumber \]
The derivative of the partition function with respect to volume is:
\[ \left(\dfrac{\partial Q}{\partial V}\right)_{N,\beta} = -\beta \sum_i{\left(\dfrac{\partial E_i}{\partial V}\right)_{N}e^{-\beta E_i(N,V)}} \nonumber \]
The average pressure can then be written as:
\[ \langle P \rangle = \dfrac{kT}{Q(N,V,\beta}\left(\dfrac{\partial Q}{\partial V}\right)_{N,\beta} \nonumber \]
Which shows that the pressure can be expressed solely terms of the partition function:
\[ \langle P \rangle = kT\left(\dfrac{\partial \ln{Q}}{\partial V}\right)_{N,\beta} \nonumber \]
We can use this result to derive the ideal gas law. For \(N\) particles of an ideal gas:
\[ Q(N,V,\beta) = \dfrac{[q(V,\beta)]^N}{N!} \nonumber \]
where:
\[ q(V,\beta) = \left(\dfrac{2\pi m}{h^2\beta}\right)^{3/2}V \nonumber \]
is the translational partition function. The utility of expressing the pressure as a logarithm is clear from the fact that we can write:
\[\begin{split} \ln{Q} &= N\ln{q}-\ln{N!} \\ &= -\dfrac{3N}{2}\ln{\left(\dfrac{2\pi m}{h^2\beta}\right)}+N\ln{V}-\ln{N!} \end{split} \nonumber \]
We have used the property of logarithms that \(\ln{(AB)} = \ln{(A)} + \ln{(B)}\) and \(\ln{(X^Y)} = Y\ln{(X)}\). Only one term in the ln \(Q\) depends on \(V\). Taking the derivative of \(N\ln{V}\) with respect to \(V\) gives:
\[ \left(\dfrac{\partial \ln{Q}}{\partial V}\right)_{N,\beta} = \dfrac{N}{V} \nonumber \]
Substituting this into the above equation for the pressure gives:
\[ P = \dfrac{NkT}{V} \nonumber \]
which is the ideal gas law. Recall that \(Nk = nR\) where \(N\) is the number of molecules and \(n\) is the number of moles. \(R\) is the universal gas constant (8.314 J/mol-K) which is nothing more than \(k\) multiplied by Avagadro’s number. \(N_Ak = R\) converts the constant from a "per molecule" to a "per mole" basis.
Gas Compressed by a Piston
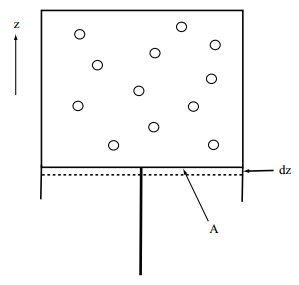
Let us consider a simple thought experiment, which is illustrated in the figure above: A system of \(N\) particles is compressed by a piston pushing in the positive \(z\) direction. Since this is a classical thought experiment, we think in terms of forces. The piston exerts a constant force of magnitude \(F\) on the system. The direction of the force is purely in the positive \(z\) direction, so that we can write the force vector \(\bf{F}\) as \(\bf{F} = \begin{pmatrix} 0, 0, F \end{pmatrix}\). At equilibrium (the piston is not moving), the system exerts an equal and opposite force on the piston of the form \(\begin{pmatrix} 0, 0, -F \end{pmatrix}\). If the energy of the system is \(E\), then the force exerted by the system on the piston will be given by the negative change in \(E\) with respect to \(z\):
\[-F = -\dfrac{dE}{dz} \label{Eq3.29} \]
or:
\[F = \dfrac{dE}{dz} \label{Eq3.30} \]
The force exerted by the system on the piston is manifest as an observable pressure \(P\) equal to the force \(F\) divided by the area \(A\) of the piston, \(P=F/A\). Given this, the observed pressure is just:
\[P = \dfrac{dE}{Adz} \label{Eq3.31} \]
Since the volume decreases when the system is compressed, we see that \(Adz = -dV\). Hence, we can write the pressure as \(P = -dE/dV\).
Of course, the relation \(P = -dE/dV\) is a thermodynamic one, but we need a function of \(x\) that we can average over the ensemble. The most natural choice is:
\[p(x) = -\dfrac{d \mathcal{E} (x)}{dV} \label{Eq3.32} \]
so that \(P = \langle p(x) \rangle\). Setting up the average, we obtain:
\[\begin{align} P &= -\dfrac{C_N}{Q(N, V, T)} \int \dfrac{\partial \mathcal{E}}{\partial V} e^{-\beta \mathcal{E} (x)} \\ &= \dfrac{C_N}{Q(N, V, T)} \dfrac{1}{\beta} \int \dfrac{\partial}{\partial V} e^{-\beta \mathcal{E} (x)} \\ &= \dfrac{kT}{Q(N, V, T} \dfrac{\partial}{\partial V} C_N \int e^{-\beta \mathcal{E} (x)} \\ &= kT \left( \dfrac{\partial \: \text{ln} \: Q(N, V, T)}{\partial V} \right) \end{align} \label{Eq3.33} \]
Ideal Gas in the Canonical Ensemble
Recall that the mechanical energy for an ideal gas is:
\[\mathcal{E} (x) = \sum_{i=1}^N \dfrac{\textbf{p}_i^2}{2m} \label{Eq3.36} \]
where all particles are identical and have mass \(m\). Thus, the expression for the canonical partition function \(Q(N, V, T)\) is:
\[Q(N, V, T) = \dfrac{1}{N!h^{3N}} \int dx \: e^{-\beta \sum_{i=1}^N \textbf{p}_i^2/2m} \nonumber \]
Note that this can be expressed as:
\[Q(N, V, T) = \dfrac{1}{N!h^{3N}}V^N \left[ \int dp \: e^{-\beta p^2/2m} \right]^{3N} \nonumber \]
Evaluating the Gaussian integral gives us the final result immediately:
\[Q(N, V, T) = \dfrac{1}{N!} \left[ \dfrac{V}{h^3} \left( \dfrac{2 \pi m}{\beta} \right)^{3/2} \right]^N \nonumber \]
The expressions for the energy:
\[E = -\dfrac{\partial}{\partial \beta} \: \text{ln} \: Q(N, V, T) \nonumber \]
which gives:
\[E = \dfrac{3}{2}NkT = \dfrac{3}{2}nRT \label{Eq3.37} \]
and pressure:
\[P = kT \left( \dfrac{\partial \: \text{ln} \: Q(N, V, T)}{\partial V} \right) \nonumber \]
giving:
\[P = \dfrac{NkT}{V} = \dfrac{nRT}{V} \label{Eq3.38} \]
which is the ideal gas law.

