16.4: The Law of Corresponding States
- Page ID
- 204042
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Johannes Diderik van der Waals modified the ideal gas law to better describe the behavior of real gases by introducing corrections to account for the finite size of molecules and the intermolecular forces between them, leading to the well-known van der Waals equation.
\[\left(P+\frac{a}{V_m^2}\right)\left(V_m-b\right)=R T \label{1}\]
This expression for the van der Waal gas involves two phenomenological constants, \(a\) and \(b\). Van der Waals postulated that all real gases at corresponding states should behave similarly and he focused on applying Equation \ref{1} at the critical point of difference gases—the unique temperature, pressure, and volume at which the distinction between liquid and gas disappears.
The corresponding state that van der Waals chose to use is called the reduced state, which is based on the deviation of the conditions of a substance from its own critical conditions. We can define reduced quantities:
\[\begin{align*} P_r &= \dfrac{P}{P_c} \\[4pt] V_r &= \dfrac{V}{V_c} \\[4pt] T_r &= \dfrac{T}{T_c} \end{align*} \]
By substitution into Equation \ref{1}, the Van der Waal equations can be expressed differently
\[ \left( P_r + \dfrac{3}{\bar{V}_r^2} \right) \left( \bar{V}_r - \dfrac{1}{3} \right) = \dfrac{8}{3} T_r \label{vdw} \]
Equation \ref{vdw} means the critical parameters for a gas can be expressed in terms of \(a\) and \(b\) parameters:
\[\begin{align*} V_c &=3b \\[4pt] P_c &=\dfrac{a}{27b^2} \\[4pt] T_c &=\dfrac{8a}{27b R} \end{align*} \]
Hence, when gases are expressed in terms of their reduced variables, the van der Waals equation takes on a universal form (Equation \ref{vdw}) that applies to all gases, regardless of their chemical identity. This discovery led van der Waals to formulate the Law of Corresponding States, which states that different gases at the same reduced temperature and reduced pressure will exhibit similar thermodynamic behavior. This principle provided a unifying framework for understanding real-gas behavior and laid the foundation for generalized equations of state and compressibility charts used in modern thermodynamics.
Although the actual pressures and volumes may differ, two gases are said to be in corresponding states if their reduced pressure, volume, and temperature are the same. What it says is that the behavior of all gases (and liquids!!) is pretty much the same, except for a scaling factor that is related to the critical point of the substance. The compressibility value (\(Z\)) of 3/8 at the critical point for the van der Waals equation is actually not in such good agreement with measurement. This is why the more complicated Redlich-Kwong and Peng-Robertson expressions are better, although the idea is the same. Hence, all one needs to know to describe any fluid's behavior is its critical point. For example, argon behaves much the same at 300 K as ethane does at 600 K because these temperatures correspond to twice their respective critical temperatures (150.72 K and 305.4 K, respectively) so \(T_r=2.0\).
Compressibility
The Compressibility provides a useful way to compare the behavior of real gases with that predicted by the ideal gas law, and it connects directly to the critical ratios first introduced by van der Waals.
\[Z = \dfrac{PV}{RT} \nonumber\]
Over the past 150 years, researchers have collected extensive experimental data on a wide variety of fluids, allowing the Law of Corresponding States to be tested and validated. When the pressure, temperature, and volume of different fluids are expressed in terms of their reduced values, their measurements can be superimposed on the same compressibility chart (Figure \(\PageIndex{1}\)). This overlap shows that most “normal” fluids, despite having different molecular structures, follow a common pattern of behavior when scaled by their critical properties.
We can rewrite the universal expression for compressibility \(Z\) using reduced variables and plot measured values of \(Z\) versus the reduced pressure, \(P_r\) (Figure \(\PageIndex{1}\)). As you can see, very different gases/liquids like nitrogen and water can be made to coincide if their properties are plotted relative to there critical points rather than in absolute terms. The compressibility factor \(Z\) can also be cast into the form of corresponding states showing that \(Z\) also can be expressed as a universal function of \(V_r\) and \(T_r\) or any other two reduced quantities:
\[Z=\dfrac{\bar{V}_r}{\bar{V}_r–\dfrac{1}{3}} – \dfrac{9}{8\bar{V}_r T_r} \nonumber \]
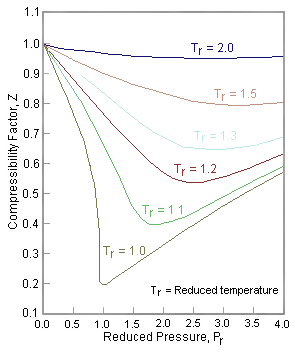
These charts show that most “normal” fluids, such as simple hydrocarbons, noble gases, and diatomic molecules, conform closely to the predictions of the Law of Corresponding States. Deviations occur mainly in more complex or strongly associating fluids—such as water, ammonia, or hydrogen fluoride—where strong polarity or hydrogen bonding introduces additional interactions not accounted for by van der Waals’ simple model. Nevertheless, the overall success of the law demonstrates its power: by scaling thermodynamic variables to the critical constants, we can describe the behavior of a wide variety of substances with a single framework. This insight not only validated van der Waals’ pioneering theory but also provided a foundation for modern equations of state and practical tools in chemical engineering and physical chemistry.
Van der Waals did not stop here. He went on to describe the root cause of condensation of gases into liquids at lower temperatures: the attractive interactions between the molecules.

